找规律

1. 计算 1！*2！*3！*....*n！的结果末尾中0的个数

先考虑如何计算单个数的阶乘n！

思路：

0实际上来源于10，而10来源于2×5，所以只需要判断n×(n−1)×(n−2)×...×1n×(n−1)×(n−2)×...×1可以拆分成多少个2×52×5即可。而2的个数明显多于5的个数，所以只需要判断有多少个5即可

考虑1到100这100个数可以分成多少个5

首先可以想到5,10,15,20,...,1005,10,15,20,...,100这100/5=20100/5=20个数可以分解成5×m5×m的形式，所以这20个数每个数都可以分出一个5来

其次考虑25,50，75，10025,50，75，100这100/5/5=4100/5/5=4个数可以分解成5×5×m5×5×m的形式，所以这4个数每个数又可以分出一个5来

注，由于计算5的倍数时25,50,75,100已经分解出一个5，所以计算25的倍数时仅剩下一个5可以分解

所以100!末尾0的个数就是5的个数即100/5+100/5/5=24100/5+100/5/5=24个

如果给出的n足够大，那么

可以分解成5×m5×m形式的数可以贡献出一个5，总共有n/5n/5个
可以分解成5×5×m5×5×m形式的数可以贡献出一个5，总共有n/5/5n/5/5个
可以分解成5×5×5×m5×5×5×m形式的数可以贡献出一个5，总共有n/5/5/5n/5/5/5个
…
参考： 每天一道LeetCode-----计算n的阶乘末尾有多少个0

意思就是计算72的阶乘，就累加72//5+72//(5*5)+72//(5*5*5)+...

n = int(input())
res = 0
for i in range(1,n+1):
    temp = 5
    while(i//temp>=1 ):
        res+=i//temp
        temp*=5
print(res)

 

 

2.  233. 数字 1 的个数

给定一个整数 n，计算所有小于等于 n 的非负整数中数字 1 出现的个数。

示例:

输入: 13
输出: 6
解释: 数字 1 出现在以下数字中: 1, 10, 11, 12, 13 。

参考：用递归实现。

举例：可以将一个数字拆分为最高位和其右边 ，比如 3452，拆成 3和 452， 最高位 high =3, last = 452,数的最高位为千位。那么power为1000,先看这个最高位贡献了多少个1。此时考虑最高位>1的时候：最高位贡献了1000个1，即从1000至1999一共有1000个1。那么剩余位1000-1999和2000-2999等贡献的1数目都一样，即看0-999贡献了多少个1，即high * countDigitOne(power-1)个1。最后还剩下3000-3452这last+1个数字的个，十，百位贡献的1的数目，即countDigitOne(last)。那么如果最高为=1呢？考虑1452这个数。首先最高为贡献了last+1个1，即从1000-1452一共（last+1）个数。然后last=452这个数又贡献了countDigitOne(last)个数，最后0-999贡献了countDigitOne(power-1)个数。

def countDigitOne(n):

    if n<=0: return 0
    if n<10: return 1
    last = int(str(n)[1:])
    power =  10**(len(str(n))-1)      
    high = int(str(n)[0])
    if high == 1:
        return countDigitOne(last) + countDigitOne(power-1) + last+1
    else:
        return power+high*countDigitOne(power-1) + countDigitOne(last);
print(countDigitOne(n))

 

3. 二进制中1的个数

输入一个long类型的数值, 求该数值的二进制表示中的1的个数 .

输入描述:

long 类型的数值（有正有负）

输出描述:

该数值二进制表示中1的个数

n = int(input())
def NumberOf1(n):
    count = 0
    while n&0xffffffffffffffff != 0:
        count += 1
        n = n & (n-1)   # 每进行这样操作，最后一位的1就会消去
    return count
print(NumberOf1(n))

或者调库：

n = int(input())
if n >= 0:
    print( bin(n).count('1'))
else:
    print(bin(n & 0xffffffffffffffff).count('1'))

 

 

168. Excel表列名称

给定一个正整数，返回它在 Excel 表中相对应的列名称。

例如，

1 -> A
2 -> B
3 -> C
...
26 -> Z
27 -> AA
28 -> AB
...
示例 1:

输入: 1
输出: "A"
示例 2:

输入: 28
输出: "AB"
示例 3:

输入: 701
输出: "ZY"

 

这道简单题其实并不直观。采用26进制的思路，但是需要注意的是0没有任何对应，所以当余数为0时，要将其置为Z，即26！

class Solution:
    def convertToTitle(self, n: int) -> str:   # 26进制
        res = ""
        while n:
            n, y = divmod(n, 26)     # 商/余数
            if y == 0:          # 单独处理，因为当余数为0，从商借1， 余数改为26，即Z
                n -= 1
                y = 26
            res = chr(y + 64) + res   # 将余数也就是进位放到当前位置（目前的最高位）
        return res

 

223. 矩形面积

在二维平面上计算出两个由直线构成的矩形重叠后形成的总面积。

每个矩形由其左下顶点和右上顶点坐标表示，如图所示。

 

 

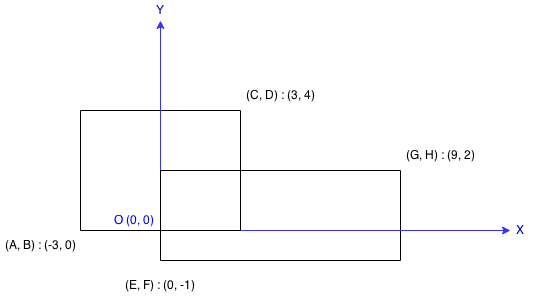
示例:

输入: -3, 0, 3, 4, 0, -1, 9, 2
输出: 45

 

思路：关键在于重叠部分的计算。为了计算重叠部分，我们要尽可能地压缩这一部分。什么意思呢？就是先算重叠部分的宽来说，我们要算这两个矩形左边的最右者*右边的最左者。计算重叠部分的高来说，我们要算这两个矩形上边的最下者和下边的最上者。

解法如下：

class Solution:
    def computeArea(self, A, B, C, D, E, F, G, H):
        overlap = max(min(C,G)-max(A,E), 0)*max(min(D,H)-max(B,F), 0)
        return (A-C)*(B-D) + (E-G)*(F-H) - overlap

 

238. 除自身以外数组的乘积

给定长度为 n 的整数数组 nums，其中 n > 1，返回输出数组 output ，其中 output[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。

示例:

输入: [1,2,3,4]
输出: [24,12,8,6]
说明: 请不要使用除法，且在 O(n) 时间复杂度内完成此题。

 

思路如下： 先对数组从左至右做一遍乘积，再对数组从右至左做一遍乘积。最后结果对应相乘即可。

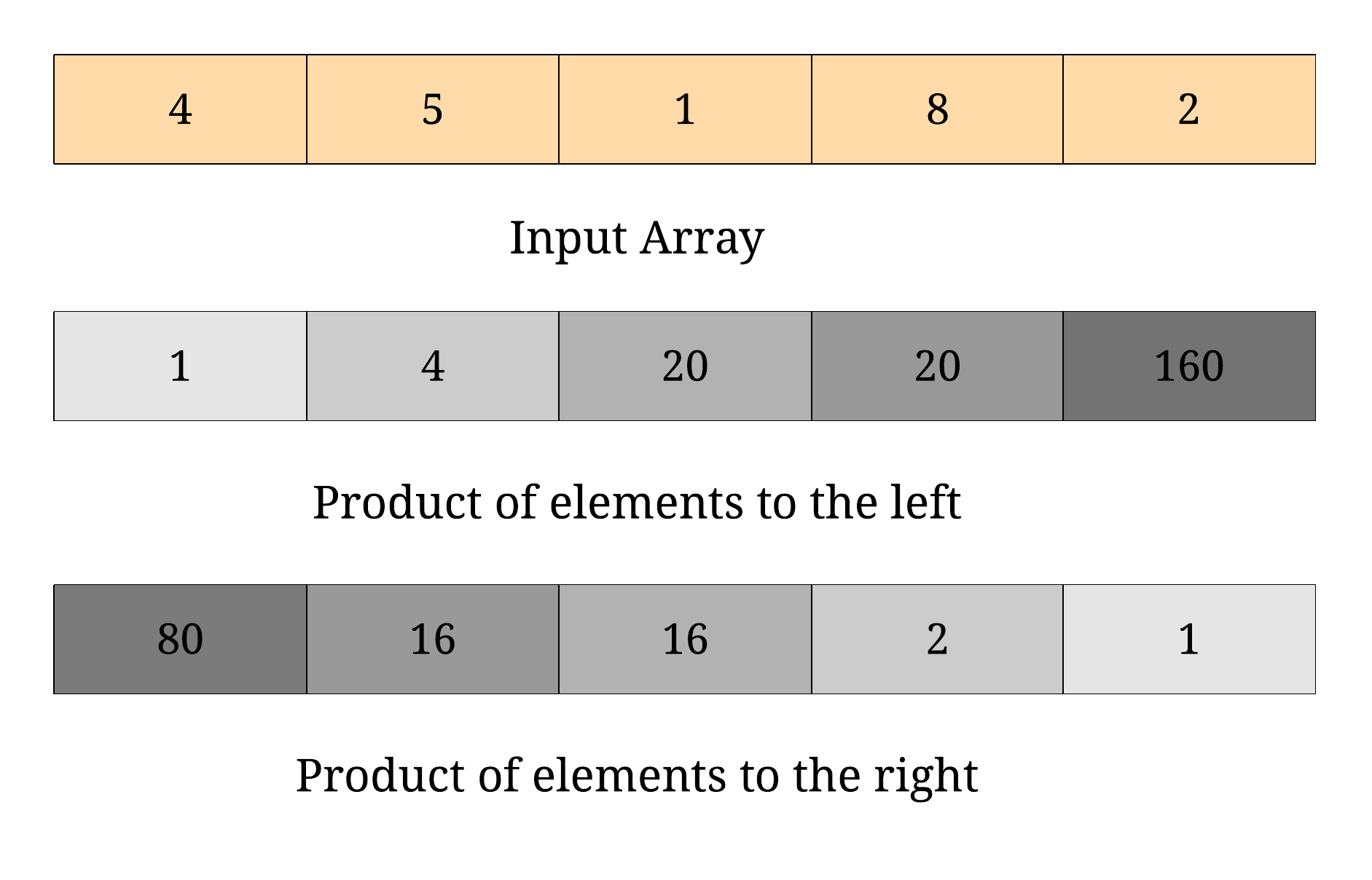
class Solution:
    def productExceptSelf(self, nums: List[int]) -> List[int]:
        temp,left,right,res = 1, [], [], []
        for i in range(len(nums)):
            left.append(temp)
            temp *= nums[i]
        temp = 1
        for i in range(len(nums)-1, -1, -1):
            right.append(temp)
            temp *= nums[i]
        for i in range(len(nums)):
            res.append(left[i]*right[len(nums)-i-1])
        return res

 

 

334. 递增的三元子序列

给定一个未排序的数组，判断这个数组中是否存在长度为 3 的递增子序列。

数学表达式如下:

如果存在这样的 i, j, k,  且满足 0 ≤ i < j < k ≤ n-1，
使得 arr[i] < arr[j] < arr[k] ，返回 true ; 否则返回 false 。
说明: 要求算法的时间复杂度为 O(n)，空间复杂度为 O(1) 。

示例 1:

输入: [1,2,3,4,5]
输出: true
示例 2:

输入: [5,4,3,2,1]
输出: false

 

思路：动态规划。写了之后发现超时。然后网上有一种很骚的解法：（注释掉的是我的DP）

class Solution:
    def increasingTriplet(self, nums: List[int]) -> bool:
     #   if len(nums)<3: return False
     #   dp = [1]*(len(nums)+1)
     #   for i in range(1,len(nums)):
     #       for j in range(i):
     #           if nums[i]>nums[j]:
     #               dp[i] = max(dp[i], dp[j]+1)
     #           if dp in 
     #    return True if 3 in dp else False
        first, second = float('inf'), float('inf')
        for i in nums:
            if i<=first:   # 找三个数中最小的那个
                first = i
            elif i<=second:     # 找其次小的那个
                second = i
            else:
                return True       # 如果有三个中最小的那个则返回True
        return False

 

414. 第三大的数 （采用上题的思路）

给定一个非空数组，返回此数组中第三大的数。如果不存在，则返回数组中最大的数。要求算法时间复杂度必须是O(n)。

示例 1:

输入: [3, 2, 1]

输出: 1

解释: 第三大的数是 1.
示例 2:

输入: [1, 2]

输出: 2

解释: 第三大的数不存在, 所以返回最大的数 2 .

 

这个题我采用了上题的思路，也是利用了两个变量： first和second。感觉做的多了就会有灵感。

class Solution:
    def thirdMax(self, nums):
        nums = sorted(list(set(nums)), reverse=True)   # 注意去重和排序是算法成立的前提
        first, second = float('-inf'), float('-inf')
        flag = False
        for i in range(len(nums)):
            if nums[i]>first:         # 找最大的那个数
                first = nums[i]
            elif nums[i]>second:      # 找第二大的那个数
                second = nums[i]
            else:
                if not flag:          # 如果有第三大的数就加入
                    third = nums[i]
                flag = True
        return third if flag else first       # 返回结果

 

用数组值做索引来实现O（n）遍历，思路非常有趣：

442. 数组中重复的数据    448. 找到所有数组中消失的数字

 

 

462. 最少移动次数使数组元素相等 II

给定一个非空整数数组，找到使所有数组元素相等所需的最小移动数，其中每次移动可将选定的一个元素加1或减1。 您可以假设数组的长度最多为10000。

思路：最终相等的这个数一定是中位数，所以先找出中位数，然后统计绝对值即可。

class Solution:
    def minMoves2(self, nums: (List[int])) -> int:
        mid = sorted(nums)[len(nums)//2]
        n = 0
        for num in nums:
            n += abs(num-mid)
        return n