关于码率自适应算法的研究
选题来自:
清华大学全球智能网络传输大赛( https://www.aitrans.online/competition_detail/competition_id=2 )
码率,是衡量视频块数据量大小的一个重要指标。离线下载视频流并不需要码率自适应算法进行支持,人们可以通过更长的时间来弥补低网络带宽所带来的代价。但若以直播形式进行视频流的播放,显然实时性特征并不允许以更长时间弥补代价,这样就会带来两种可能情况:
- 第一种情况就是视频流码率较高而网络带宽较低,当缓冲区中已缓存的视频块输出完后,由于网络带宽较低,高码率视频块还未来得及下载完成,这时就会导致卡顿现象;
- 第二种情况即相反,视频流码率较低而网络带宽较高,视频会流畅地播放直至结束,但多余网络带宽被浪费。
在上述第二种情况中,显而易见,观看者体验能够利用多余网络带宽进行提升。码率自适应算法的意义,就是将码率与网络带宽相关联,实现码率在一定规则下随网络带宽进行调整,尽可能减少网络带宽的浪费,提升观看者体验。
1数据分析
1.1视频流数据
进行关于码率自适应算法的研究,首先是需要对数据进行分析处理。很显然,在直播视频流中存在两种数据,一是视频流数据,另一是网络带宽数据。要实现码率自适应,视频流数据的作用在于判断下一视频块是否为I帧,即第一帧,而关键在于对网络带宽的预测,以实现码率在第一帧时进行调整。接下来,让我们查看视频流数据以及重点分析网络带宽数据。
| 时间戳(s) | 帧数据大小(bit) | 是否为I帧(0/1) |
|---|
表1.1.1 视频流数据格式
读取视频流数据查看是否符合格式:
成功读取文件:frame_trace_0
时间戳(s) 帧数据大小(bit) 是否为I帧(0/1)
0 -2.000 149944.0 1
1 -1.958 296.0 0
2 -1.917 192.0 0
3 -1.875 30768.0 0
4 -1.833 7304.0 0
...
由读取结果可知,视频流数据格式正如表格所示。
1.2网络带宽数据
| 时间戳(s) | 吞吐量(Mbps) |
|---|
表1.2.1 网络带宽数据格式
同1.1部分的原理,对网络带宽数据进行查看以及分析:
成功读取文件:0
时间戳(s) 吞吐量(Mbps)
0 0.0 2.852570
1 0.5 3.599259
2 1.0 2.166463
3 1.5 1.249071
4 2.0 1.045936
...
网络带宽数据格式也如表格所示。
上述方式仅仅能够对网络带宽数据的格式进行了解,并不能知晓数据分布情况,接下来尝试观察各个网络的基本统计情况,以便能在后续分析中起到作用。
| NET | AVG | VAR | MIN | MAX | MEDIAN | STD | NUM |
|---|---|---|---|---|---|---|---|
| 0 | 1.639240 | 0.631950 | 0.2 | 6.073426 | 1.496345 | 0.794953 | 5880 |
| 1 | 1.646814 | 0.623782 | 0.2 | 5.554752 | 1.501850 | 0.789799 | 5880 |
| 2 | 1.572694 | 0.572780 | 0.2 | 5.116822 | 1.431559 | 0.756822 | 5880 |
| 3 | 1.632853 | 0.668005 | 0.2 | 5.697373 | 1.478645 | 0.817316 | 5880 |
| 4 | 1.590489 | 0.599625 | 0.2 | 5.316171 | 1.463746 | 0.774355 | 5880 |
| 5 | 1.582860 | 0.623535 | 0.2 | 5.066436 | 1.425337 | 0.789643 | 5880 |
| 6 | 1.620369 | 0.651305 | 0.2 | 5.999323 | 1.460636 | 0.807035 | 5880 |
| 7 | 1.630145 | 0.623611 | 0.2 | 5.164020 | 1.486162 | 0.789690 | 5880 |
| 8 | 1.691533 | 0.679450 | 0.2 | 5.218475 | 1.558886 | 0.824288 | 5880 |
| 9 | 1.598350 | 0.602484 | 0.2 | 5.528585 | 1.459685 | 0.776198 | 5880 |
| 10 | 1.648675 | 0.842234 | 0.2 | 5.833054 | 1.471185 | 0.917733 | 5880 |
| 11 | 1.489905 | 0.652282 | 0.2 | 5.829624 | 1.316017 | 0.807640 | 5880 |
| 12 | 1.613366 | 0.779983 | 0.2 | 6.344063 | 1.452590 | 0.883166 | 5880 |
| 13 | 1.548199 | 0.727855 | 0.2 | 5.749135 | 1.354811 | 0.853144 | 5880 |
| 14 | 1.652967 | 0.770559 | 0.2 | 6.190227 | 1.490519 | 0.877815 | 5880 |
| 15 | 1.557120 | 0.752587 | 0.2 | 5.811503 | 1.353709 | 0.867518 | 5880 |
| 16 | 1.679373 | 0.805341 | 0.2 | 5.687441 | 1.524697 | 0.897408 | 5880 |
| 17 | 1.598344 | 0.743242 | 0.2 | 5.688606 | 1.425693 | 0.862115 | 5880 |
| 18 | 1.544045 | 0.692877 | 0.2 | 5.919803 | 1.363475 | 0.832392 | 5880 |
| 19 | 1.654456 | 0.771029 | 0.2 | 5.507541 | 1.477009 | 0.878083 | 5880 |
表1.2.2 各个网络的基本统计情况
接着我们通过散点图来观察网络带宽数据的变化,并且我们仅以一部分文件进行可视化,并不全部进行可视化。
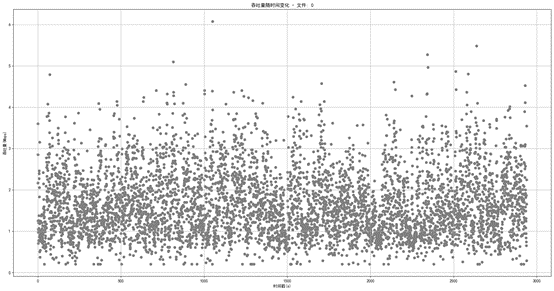
图1.2.1 网络0数据带宽散点图
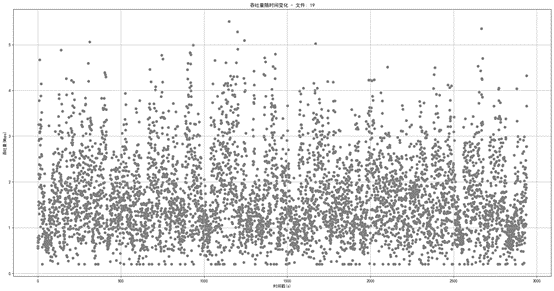
图1.2.2 网络19数据带宽散点图
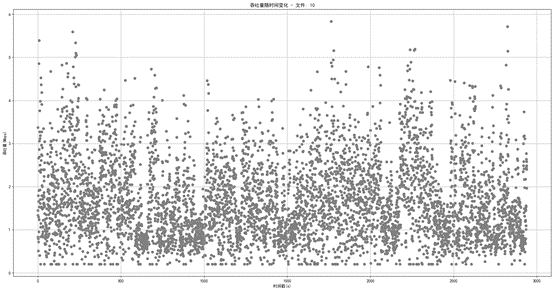
图1.2.3 网络10数据带宽散点图
通过上述一部分网络带宽数据的散点图能够看出来,网络带宽的波动性是比较明显的,在各个时间戳都存在着大吞吐量以及小吞吐量,大部分情况下,各时间戳吞吐量极差是比较大的。
散点图反映上述几个网络的带宽分布情况,但并不具备特征性。在上述过程中,已经得出各个网络的基本统计情况,其中包括均值、方差、中位数等。均值可以反映网络带宽总体的一般情况和分布的集中趋势,而方差则可以反映网络带宽的波动性,下面通过折线图对几个特殊情况网络带宽进行反映。
- 网络10 - 方差最大,为0.84,即网络10的带宽波动最大。

图1.2.4 网络10数据带宽折线图
- 网络2 - 方差最小,为0.57,即网络2的带宽波动最小。
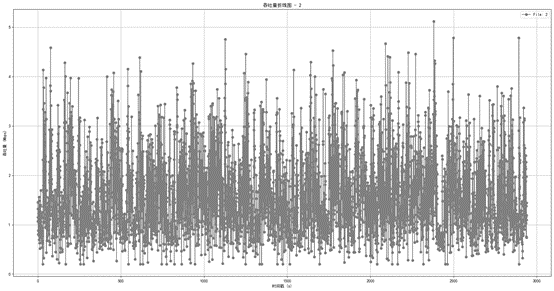
图1.2.5 网络2数据带宽折线图
- 网络8 - 均值最大,为1.69,反映网络8的带宽相对集中在1.69Mbps。
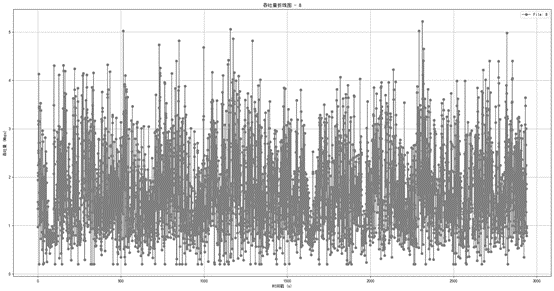
图1.2.6 网络8数据带宽折线图
- 网络11 - 均值最小,为1.49,反映网络11的带宽相对集中在1.49Mbps。
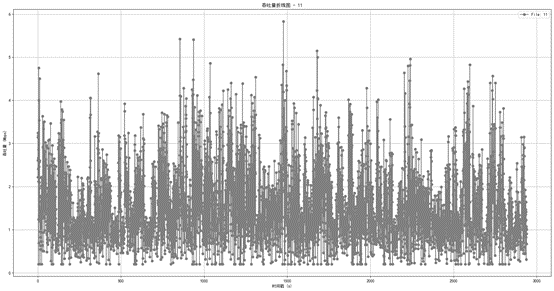
图1.2.7 网络11数据带宽折线图
通过均值最大以及均值最小的情况,能够得知已得的20个网络带宽相对集中在1.49Mbps至1.69Mbps之间。并且由方差的极差可以得知,各个网络的波动幅度是相差不多的。
1.3网络带宽预测
在对网络带宽数据进行可视化后,接下来尝试对网络带宽进行预测。要对网络带宽进行预测,最重要的是由已知数据实现对t+1时刻的网络带宽进行预测。
要实现预测,最常用的方法是拟合,原理是利用现有已知数据拟合函数,再代入需要预测的节点数据得出预测结果。下面以网络0为例展示拟合方法。
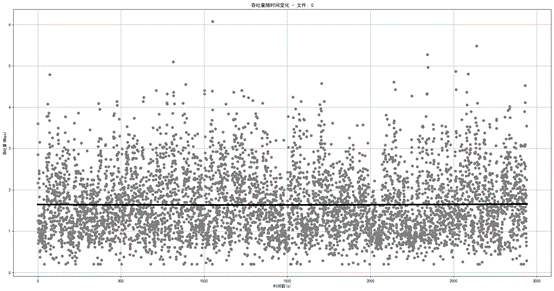
图1.3.1 网络0带宽二次拟合图
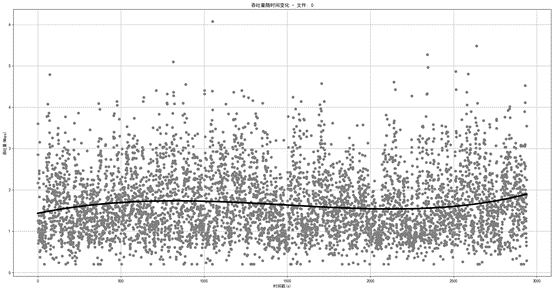
图1.3.2 网络0带宽四次拟合图
上述两种拟合都是运用的最常用的多项式拟合,可以发现在二次拟合时,拟合函数呈一条直线,四次拟合时呈一条曲线,拟合效果并不好。设想一下,如果再利用更高的多项式去对数据进行拟合,会更加地贴合,呈现出网络带宽波动的趋势,但实现并不简单,选择多高的次数难以抉择,低次数无法贴切拟合,高次数则会增加计算、降低效率。因此,多项式拟合的方式应该是不合理的。
或许也可以使用机器学习算法(如决策树、神经网络等)对网络带宽数据进行学习拟合?仔细思考一下能够发现利用拟合进行预测分析的方向是行得通的,但网络带宽对时间是敏感的,这决定着网络的波动并不存在一个整体的趋势,而是在某个时间段呈现一个小的波动趋势,所以对整段时间的网络带宽进行拟合是不合理的,应该改变思路,选择某一时间段的网络带宽数据进行拟合预测。
若仅仅是对某一时间段的网络带宽数据进行拟合,一个关键问题是如何选择时间段才能生成更贴合的拟合函数进行预测,而网络带宽对时间波动明显,一个好的思路当然是实现动态地选择,不过这似乎难以实现,粗略思考会发现需要存储所有时间戳数据并时时计算分析趋势,存储代价以及计算代价都较高。但若固定一个静态不变的时间段,时间段过短则拟合效果会大打折扣,时间段过长就会陷入选择最高次的困难当中。
显然,运用拟合的方法进程预测分析困难重重。数学建模中,拟合是很重要的方法,但在实际当中对于过于复杂的数据,插值方法更为人所倾向。常用插值方法有拉格朗日插值以及牛顿插值,但拉格朗日插值并不具备继承性,不满足持续预测的需求以及需要重复计算的过高代价,若二选其一,我们选择牛顿插值方法。
但若选择牛顿插值依旧存在些问题,O(n2)的时间复杂度完全不能符合实时性的特征,而且在大量的网络带宽数据中运用牛顿插值可能会出现震荡现象,那就需要对插值方法进行优化。而数学建模中,存在优化的插值方法,最常用的即样条插值。综合分析来看,我们选择样条插值方法来对网络带宽进行预测分析。
三次样条插值是最常用的插值方法之一。它在每个区间上使用三次多项式,能够提供平滑的曲线,并且在每个数据点处一阶和二阶导数连续。在平滑性和计算复杂性之间取得了良好的平衡。
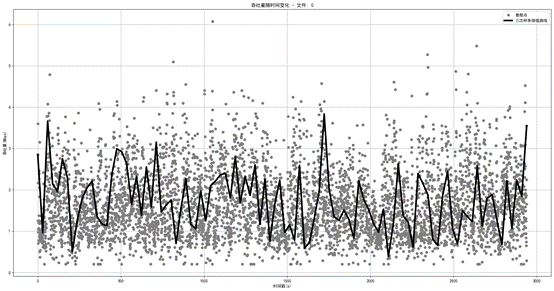
图1.3.3 网络0带宽三次样条插值图
但是如果需要更高的平滑度,可以选择五次样条插值。所以再试着利用五次样条插值查看平滑效果是否更好。
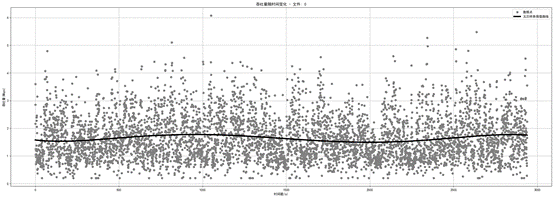
图1.3.4 网络0带宽五次样条插值图
如图,五次样条插值的预测不如三次样条插值,曲线平滑但带来的效果并不好,忽略了数据的变化性趋势,只能反映整个趋势。
综上所述,可以选择三次样条插值方法对网络带宽进行预测。在预测功能得到实现后,如果需要持续预测,则可以通过持续调用实现。其中为了防止预测过度,可以对预测值与最终值进行平均,这种方式是采取的一种保守的策略。
三次样条插值法虽然能够比较准确地拟合网络带宽数据,但由于网络带宽的波动是不具有规律的,而三次样条的基本原理是分段拟合,并且三次样条所采用的数据点并不足够多,所以在预测方面是可能出现较大误差的。对此,也有其他的方法解决问题,如区间分段,将整个数据分布区间进行划分,然后对各个区间的网络带宽数据进行平均,再对均值进行拟合预测。
2默认算法BBA分析
对于算法评估,采用的评价指标为QOE,此中QOE计算公式为:
其中bitrate为码率,rebuf为卡顿时间,latency为延迟时间。根据公式可知,若QOE越大,则码率越高,卡顿时间以及延迟时间越短,即用户体验越好。
首先来对默认的BBA算法进行运行查看,可得结果:
video count 0 2325.938463842154
video count 1 2134.2679427599883
video count 2 2099.2567129859885
video count 3 1883.6156018468353
video count 4 2039.8110413030392
video count 5 2017.197424985265
video count 6 2214.2379477074905
video count 7 1787.1202264559956
video count 8 1986.7208565188107
video count 9 2018.3328661650835
video count 10 1997.8216563325327
video count 11 2084.5396934050314
video count 12 2167.019287243014
video count 13 2103.4136760747424
video count 14 2138.457610233685
video count 15 2041.492985012926
video count 16 2134.6470381751587
video count 17 2205.3716390914174
video count 18 2126.332732201417
video count 19 2111.6922670364993
41.61728766937708
结果直接给出最终的QOE,可以看出各video count下载时的评价指标是较为稳定的,一般情况下存在的波动是比较小的,偶尔会出现波动很大的情况,但很快会趋于稳定,并且是能够根据网络带宽进行码率的调整的。除此之外,并不能在此结果中获得更多有用的信息以对默认算法进行分析,那么接下来可以利用控制变量法的思想,修改一些参数进行比对实验分析。
2.1码率
现已知有可选码率如下表:
| Bitrate(kbps) | 500 | 850 | 1200 | 1850 |
|---|
表2.1.1 默认码率表
根据控制变量法的思想,可以选择比原码率表一高一低的码率表进行结果比对,当然,此处只做比较简单的对比,结果可能具有偶然性。
| Bitrate(kbps) | 2500 | 5000 | 10000 | 15000 |
|---|
表2.1.2 更高码率表
| Bitrate(kbps) | 100 | 300 | 700 | 1200 |
|---|
表2.1.3 更低码率表
将三种码率表的结果进行可视化,可得对比图如下:
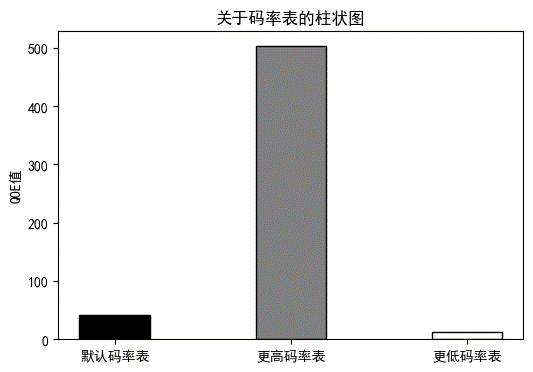
图2.1.1 三种码率表对比图
由对比图可以看出,换用更高码率表后,能够看出QOE指标是增大的,而且码率如果增大明显,QOE指标增大的也很明显。在换用更低码率表后看得出来,可选码率降低后,QOE指标也在降低。
由上述两种情况与默认情况对比可以看出,BBA算法对码率是比较敏感的,更高的码率给用户体验的提升也是较为明显的。
2.2缓冲区阈值
码率与缓冲区在视频流媒体传输中相辅相成,BBA是基于码率的算法,但若缓冲区大小设置不合理,那么也是无法给用户体验带来太大提升的,所以再接着来看看缓冲区对BBA的影响。
缓冲区的大小并不会直接对码率的调整产生影响,毕竟大的缓冲区配合拥塞的网络一样会造成卡顿现象,但阈值的设置决定着算法调整码率的时机,剩余缓冲区大小比总缓冲区大小对码率的选择所带来的影响是要大得多的。现在已知缓冲区阈值被默认设置为0.4,来看看更大或更小阈值的影响。
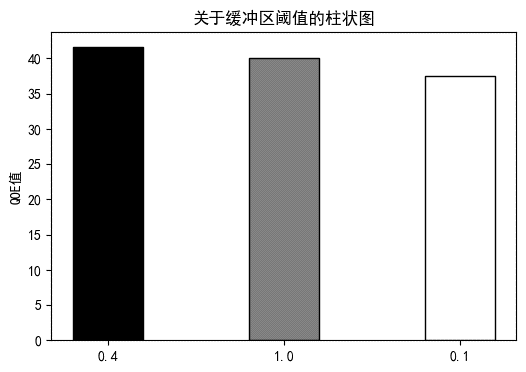
图2.2.1 三种缓冲区阈值对比图
由对比图可以看出,阈值为0.1时QOE指标比阈值为0.4时要小一些。阈值为1.0时QOE指标也比阈值为0.4时要小一些,甚至比阈值为0.1时还要小些。
由上述两种情况可以看出缓冲区阈值的大小与服务质量并不是简单的线性关系,缓冲区阈值的大小讲究合适,需要考虑多方面因素,例如:网络流量、传输速率等。
2.3卡顿时间与延迟时间
根据QOE指标的计算公式,再来看看卡顿时间rebuf以及延迟时间latency因素的影响。
在示例代码中,rebuf表示重缓冲时间,而end_delay表示端到端延迟。它们的具体计算逻辑由fixed_env.Environment类中的get_video_frame 方法实现。
提取get_video_frame方法的一部分来查看rebuf的计算逻辑:
# CDN无法获取帧的情况的rebuf
if 如果 当前时间 < CDN到达时间且 不是视频结束∶
CDN重缓冲时间 = CDN到达时间 - 当前时间
if 不是缓冲状态∶
if 缓冲区大小 > CDN重缓冲时间 * 播放持续时间权重∶
缓冲区大小 -= CDN重缓冲时间 * 播放持续时间权重
播放时间 += CDN重缓冲时间 * 播放持续时间权重
重缓冲 = 0
else∶
播放时间 += 缓冲区大小
重缓冲 = CDN重缓冲时间 - (缓冲区大小 / 播放持续时间权重)
缓冲区大小 = 0
缓冲状态 = 真
如果当前时间小于CDN到达时间,表示CDN还没有帧可用。cdn_rebuf_time计算为CDN到达时间与当前时间的差值。
如果缓冲区足够,则不发生重缓冲,即rebuf = 0。如果缓冲区不足,则计算重缓冲时间为cdn_rebuf_time减去缓冲区中可用的播放时间。
# 正常播放情况下的rebuf
if 不是视频结束∶
如果 缓冲区大小 > 持续时间 * 播放持续时间权重∶
缓冲区大小 -= 持续时间 * 播放持续时间权重
播放时间 += 持续时间 * 播放持续时间权重
重缓冲 = 0
else∶
播放时间 += 缓冲区大小
重缓冲 = 持续时间 - (缓冲区大小 / 播放持续时间权重)
缓冲区大小 = 0
缓冲状态 = 真
在正常播放情况下,如果缓冲区足够,则不发生重缓冲,即rebuf = 0。如果缓冲区不足,则计算重缓冲时间为duration减去缓冲区中可用的播放时间。
接下来再查看end_delay的计算逻辑:
延迟 = (最新帧 - 视频块计数器) * 帧时间长度 + 缓冲区大小
延迟计算为最新帧与当前视频块计数器之间的差值乘以帧时间长度,再加上当前缓冲区的大小。
由提取的代码可知,rebuf和end_delay的计算与缓冲区大小息息相关。在此并不直接修改两个参数的计算逻辑,而通过修改缓冲区大小间接查看两者对BBA算法的影响。
已知默认缓冲区大小有表记录:
| Target_buffer(s) | 2.0 | 3.0 |
|---|
表2.3.1 默认缓冲区大小表
依旧按照2.2缓冲区阈值部分的思路,换用更高与更低的缓冲区大小表进行对比。
| Target_buffer(s) | 4.0 | 6.0 |
|---|
表2.3.2 更高缓冲区大小表
| Target_buffer(s) | 0.0 | 1.0 |
|---|
表2.3.3 更低缓冲区大小表
换用三种缓冲区大小表后,有对比结果如下:
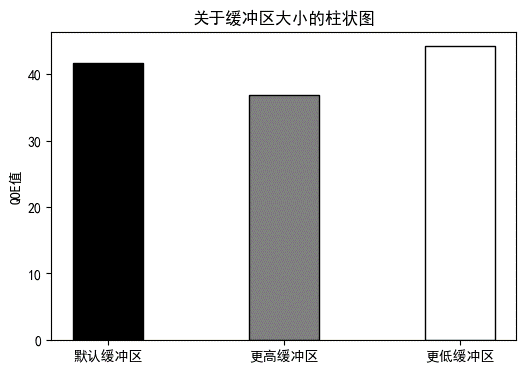
图2.3.1 三种缓冲大小表对比图
由对比图可以看出,换用更高缓冲区表时服务质量比之默认缓冲区大小要低些。换用更低缓冲区表时服务质量比之默认缓冲区大小要高些。
经过上述高低两种情况的对比,能够看出缓冲区的大小会影响重缓冲时间rebuf以及延迟时间latency,进而会影响BBA算法运行的效率,就上述情况而言,可以得出简单结论:缓冲区变大会降低服务质量。
但这结论并不能站住脚,根据我们提取到的计算逻辑来看:
- 对于rebuf,当缓冲区增大时,rebuf的值可能会减少,尤其是在 CDN 无法获取帧的情况下,缓冲区的增大可以减少重缓冲的时间。然而,如果缓冲区足够大以支持播放,则rebuf将保持为 0。
- 对于end_delay,当缓冲区增大时,end_delay通常会增加,因为它直接依赖于缓冲区的大小。更大的缓冲区意味着在等待新帧时,播放器可以存储更多的帧,从而可能导致延迟的增加。
因此,缓冲区的增大对rebuf和end_delay的影响是复杂的,具体取决于当前的播放状态和网络条件等因素。
到此,性能指标分析的部分完成。可以得出大概的结论是:码率对BBA算法的影响最明显;缓冲区阈值对BBA算法的影响非线性,是一个复杂的问题,要考虑多方面的因素;缓冲区大小对重缓冲时间的影响也较为复杂,对延迟时间的影响十分直接,两类时间都对BBA算法的运行起消极贡献。
2.4BBA算法优缺点
通过对BBA算法的性能指标分析,也能够得知一些关于BBA算法的特点。
# BBA算法伪码
if 缓冲区 <阈值∶
比特率 = 0
else if 缓冲区 >=阈值 +保护值∶
比特率 = 2
else if 缓冲区 >=保护值 +保护值∶
比特率 = 3
else∶
比特率 = 1
首先,BBA算法实现十分简单。可以由代码部分得知,逻辑简单的同时,功能实现也十分简单,主要基于缓冲区水平变化码率。
其次,BBA算法的适应性较强,分析过程中,不论是高低码率还是大小缓冲区的变化,BBA算法都能适应运行,尽管对于不同情况会存在差异,但都在一定程度上提高用户的体验。
当然,BBA算法由于是通过监控缓冲区的状态来调整视频流的码率,所以存在一些缺点:
第一,不考虑网络带宽预测:BBA算法主要依赖缓冲区状态,而不主动预测未来的网络带宽变化,可能在某些情况下无法充分利用可用带宽。
第二,可能导致次优的码率选择:由于只关注缓冲区状态,BBA算法可能在网络条件允许的情况下选择较低的码率,导致视频质量不佳。
第三,缺乏对用户体验的直接优化:BBA算法没有直接考虑用户体验指标(如视频质量、卡顿时间等),可能在某些情况下无法提供最佳的观看体验。
3BBA替代算法
在默认算法BBA分析中,已经得知BBA算法实现简单、适应性也较强,最主要的缺点在于BBA算法基于缓冲区水平调整码率。要设计一种算法替代BBA算法,最简单的思路就是优化BBA算法。
3.1替代算法设计与实现
在2.4BBA算法优缺点部分,能够得知BBA算法代码十分简洁,仅仅考虑缓冲区的状态,没有考虑重缓冲、CDN帧的情况,首先来为其添加更多情况的选择判断,提高BBA算法的全面性。
# 第一次改进
if 存在重缓冲∶比特率=0
if CDN存在帧可获取∶比特率=0
下图展示原BBA算法以及第一次BBA算法改进结果的对比:
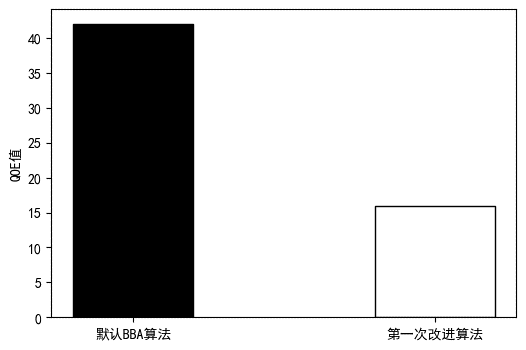
图3.1.1 原BBA算法与第一次改进算法对比图
可以看出,在添加重缓冲以及CDN帧等判断后,QOE指标降低明显,导致这种结果的原因有两方面:一是重缓冲方面,二是CDN帧方面,所以可以分开来分析。
首先,来分析是否由于重缓冲过多,导致服务质量降低,将CDN帧判断条件删除。得出与第一次改进算法的对比:

图3.1.2 第一次改进算法与删除CDN帧判断的对比图
由运行结果可以看出,仅仅添加重缓冲判断与重缓冲、CDN帧判断同时添加的结果是相同的,那么影响服务质量的就是重缓冲过多的缘故。在对BBA算法的更改中,能够发现对存在重缓冲的情况是“零容忍”,直接将码率调为最低,显然过于严格,尽管视频加载速度快,但视频观感不好。接下来,对重缓冲的处理逻辑进行优化。
已知rebuf变量记录着重缓冲时间,当重缓冲时间并不长时,可以允许重缓冲的存在,这需要设置一个阈值进行限制,此处我们设置为0.5(second);但如果重缓冲时间过于长而影响视频加载,就需要调整码率,而码率的调整,我们改为“怀柔”政策,即一级一级向下调整,而不直接降为最低。
原BBA算法与第二次改进算法对比结果如下:

图3.1.3 原BBA算法与第二次改进算法对比图
由结果和原BBA算法的比对,能够看出改进算法的服务质量已经十分接近于原BBA算法,并且原BBA算法进行视频加载的时间(测试运行时间)在2min30s左右,而改进算法进行视频加载的时间仅仅在1min左右,效率提升明显。
在补充原BBA算法的全面性后,再来试着进一步优化改进算法。已知原BBA算法最主要的缺陷在于忽略网络带宽的预测。
在实验给出的代码中,直接预测网络带宽并不有效,因为网络带宽的单位为比特每秒,而实验中多以秒为单位,衡量缓冲区大小、重缓冲严重程度等。但预测是有效的,可以适当提前作出码率的调整。
由于原BBA算法是基于缓冲区状态的算法,而缓冲区状态也能在一定程度上反应网络状况,所以可以尝试对缓冲区进行预测。而在1.3网络带宽预测部分,已经利用三次样条插值对网络带宽进行预测,在此也能够利用三次样条插值对缓冲区大小进行预测。
对于预测得知的缓冲区,依旧采取“怀柔政策”,如果缓冲区未来预期好,可以适当往上一级提升码率,但如果预期并不好,也可以适当向下一级降低码率。
# 第三次改进
三次样条预测下一时间戳的缓冲区大小
if 预测缓冲区<阈值 and 比特率 > 0∶比特率 -=1
if 预测缓冲区>保护值+保护值 and 比特率 < 3∶比特率 +=1
原BBA算法与第三次改进算法对比结果如下:
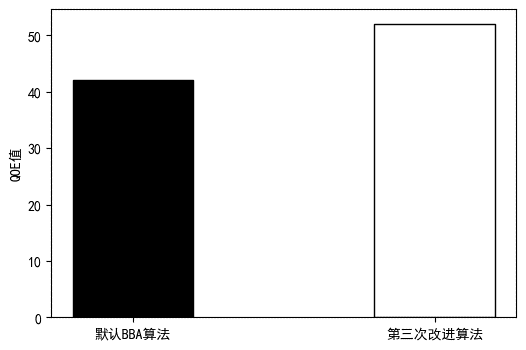
图3.1.4 原BBA算法与第三次改进算法对比图
加入预测部分后,改进算法的服务质量已经超过原BBA算法,不过由于预测的计算的增加,视频加载时间也有所增加,在1min40s左右,但依旧优于原BBA算法。当然,预测不仅仅是可以利用提及的三次样条插值法,也可以通过机器学习中决策树等算法进行预测,可能会取得更好的效果。
为什么改进算法会比默认BBA算法取得的QOE指标要高?第一,改进算法是基于BBA算法优化的,本质上还是根据对缓冲区状态的依赖进行码率的调整。第二、改进算法增加重缓冲判断以及缓冲区预测,在码率调整方面更加优化,减少码率调整的次数,进而降低重缓冲时间。根据QOE指标的计算公式,我们得知码率为QOE指标做积极贡献,重缓冲对QOE指标作消极影响,改进算法在尽可能保持码率的同时减少重缓冲时间,所以提升了QOE指标。
但改进算法也存在一些缺点,比如重缓冲判断的部分,仅仅每次调整一次,这样并不会保证下一次调整前符合条件,这样就会导致再次调整,显得重缓冲判断有些无效,对此可以利用QOE指标对码率选择结果进行评估,选择QOE指标高的码率以此改进算法。
3.2改进算法的分析
改进算法的分析,依照2默认算法BBA分析思路,分三个方面进行。
3.2.1码率
下图展示了包含原BBA算法以及改进算法关于码率表变化的对比结果:

图3.2.1.1 码率表变化对比图
从对比图可以看出,码率对改进算法的影响依旧明显,换用更高码率表后,服务质量比使用默认码率表时提升十分多,并且比原BBA算法提升的幅度要更高一些。换用更低码率后服务质量也随之降低,但对比起原BBA算法,改进算法对低码率带来的服务质量降低影响是要更小一些的。
3.2.2缓冲区阈值
依旧将缓冲区阈值由0.4分别改为0.1和1.0,观察更高缓冲区阈值和更低缓冲区阈值时改进算法的性能变化。
下图展示了包含原BBA算法以及改进算法关于缓冲区阈值变化的对比结果:
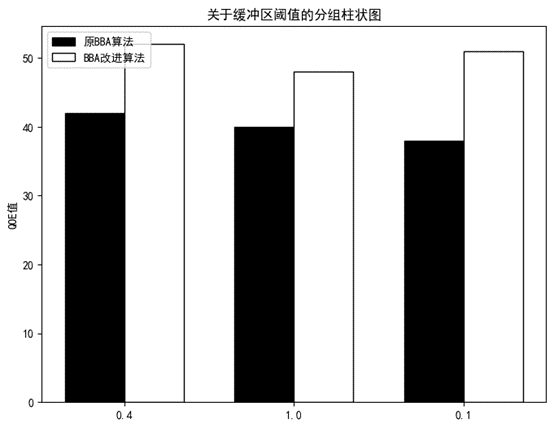
图3.2.2.1 缓冲区阈值变化对比图
从对比图可以看出缓冲区阈值变小为0.1后,服务质量确实降低,但降低幅度十分小,可以忽略不记。当缓冲区阈值变大为1.0后,服务质量也变低了,并且比缓冲区阈值变小的情况要更加低一些,变化情况同原BBA算法有些区别。经过对比也能够证明缓冲区阈值并不是越大越适合的观点。
3.2.3卡顿时间与延迟时间
还是同样的道理,通过修改缓冲区大小,间接观察卡顿时间与延迟时间对改进算法的影响。
下图展示了包含原BBA算法以及改进算法关于缓冲区大小变化的对比结果:
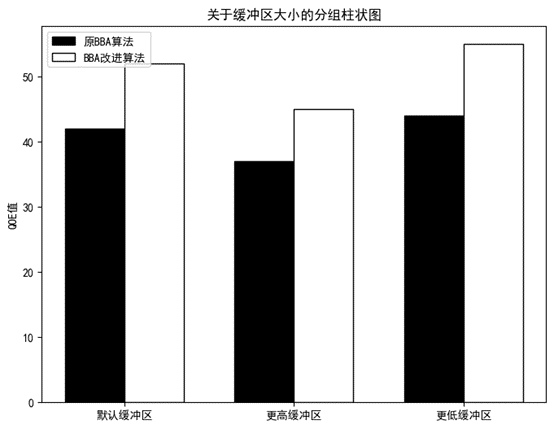
图3.2.3.1 缓冲区大小变化对比图
由对比图可以看出,换用更高缓冲区大小表后,改进算法服务质量降低。换用更低缓冲区大小表后,改进算法的服务质量提高。由此可以进一步验证在原BBA算法关于卡顿时间与延迟时间分析的结论:卡顿时间rebuf受缓冲区大小的影响是复杂的。
在对改进算法的性能分析中,同样分析了码率、缓冲区阈值以及卡顿时间和延迟时间的影响,能够看出,改进算法受到这些性能指标的影响效果是与原BBA算法类似的,这也是能够理解的,因为改进算法的基础依旧是原BBA算法。但对于这些性能指标,改进算法是存在一些变化的:码率对改进算法的影响要更大一些,缓冲区阈值对改进算法的影响要更小一些。
4不同网络环境对于BBA改进算法的性能影响
现有四种带宽类型的网络:high、low、medium以及mixed类型。保持视频流数据来自同一处,接着对这些网络下自适应算法的运行结果进行查看。
下图展示四种类型网络运行结果的对比图:
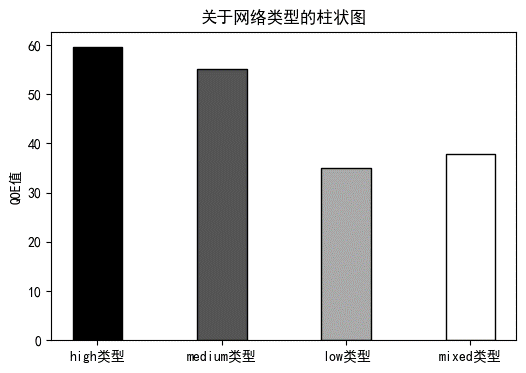
图4.1 网络类型柱状对比图
由以上四种不同网络环境下BBA改进算法运行的结果对比可知,网络环境是会对BBA改进算法产生影响的,在高速、中速网络环境下BBA改进算法都能取得比较好的效果,但在低速网络环境以及混合网络环境下,BBA改进算法的运行效率就会打个折扣。不过经过对比也能看出,BBA改进算法对于混合网络,即比较复杂的网络环境也是可以取得比较不错的效果的,能够一定程度上适应网络的波动。
在网络带宽数据分析的部分,已经得知网络10方差最大,网络2方差最小,来看看对于稳定与不稳定网络情况BBA改进算法的运行情况:

图4.2 稳定网络柱状对比图
此处可以看出网络波动情况对改进算法的影响并不太大,改进算法在稳定网络或者波动网络下运行的情况大致相同,反映出改进算法对网络的一定的适应性,对于不同的网络都够对用户所享受的服务质量进行提升。但是也有可能是因为两个网络的波动差异并不大,在网络带宽数据分析部分已经得出这一结论。
5不同视频对于BBA改进算法的性能影响
选取了三中不同来源的视频数据进行对比:
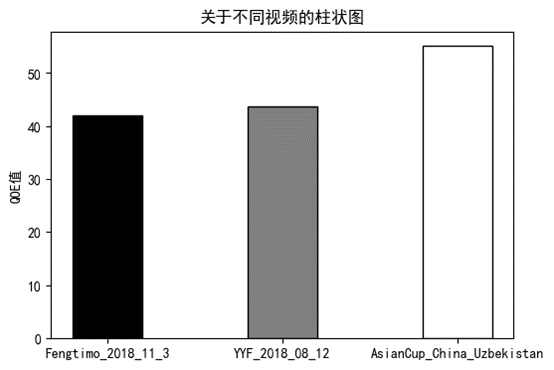
图5.1 不同视频柱状对比图
在同一网络环境下,对不同的视频,BBA改进算法执行的效果会存在一些差距,出现差异的原因,根据控制变量的思维观察,码率表的设置相同,缓冲区阈值的设置相同,那么导致这些差异的原因最可能是卡顿时间以及延迟时间,尽管缓冲区大小的设置也是相同的,但已经分析过:影响卡顿时间以及延迟时间的因素多样,因此猜测卡顿时间以及延迟时间是导致在同一网络环境下,对不同的视频,BBA改进算法服务质量的得分出现差异的主要原因。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号