Patterns in property specifications for finite-state verification
PATTERN 系列之一
- 注:pattern 指的是需求文档中的模式,pattern 系列是我看的几篇关于pattern的论文的学习总结。这几篇论文归纳了数种pattern specification。
- pattern系列讲述的内容也主要是跟软件的需求文档相关
definition
premise: An LTL formula can be satisfied by an infinite sequence of truth evaluations of variables in AP .
w = a0,a1,a2,... be such an ω-word
w(i) = ai
wi = ai,ai+1,..., which is a suffix of w
the satisfaction relation 
- w
p if p ∈ w(0)
- w
¬ψ if w
ψ
- w
φ ∨ ψ if w
φ or w
ψ
- w
X ψ if w1
ψ (in the next time step ψ must be true)
- w
φ U ψ if there exists i ≥ 0 such that wi
ψ and for all 0 ≤ k < i, wk
φ (φ must remain true until ψ becomes true)
which can be displayed in another way:
- p ∈ w(0) → w
p
- w
ψ → w
¬ψ
- w
φ ∨ w
ψ → w  φ ∨ ψ
- w1
ψ → w
X ψ (in the next time step ψ must be true)
- ∀ i ≥ 0 s.t. wi
ψ ∧ ∀0 ≤ k < i, wk
φ → w
φ U ψ (φ must remain true until ψ becomes true)
Semantics
| Textual | Symbolic | Explanation | Diagram |
|---|---|---|---|
| Unary operators↓ | |||
X  |
 |
neXt:  has to hold at the next state. has to hold at the next state. |
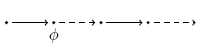 |
F  |
 |
Finally: eventually has to hold (somewhere on the subsequent path). |  |
G  |
 |
Globally:  has to hold on the entire subsequent path. has to hold on the entire subsequent path. |
 |
| Binary operators↓ | |||
 U U  |
 |
Until:  has to hold at least until has to hold at least until  becomes true, which must hold at the current or a future position. becomes true, which must hold at the current or a future position. |
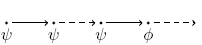 |
 R R |
 |
Release:  has to be true until and including the point where first becomes true; if has to be true until and including the point where first becomes true; if  never becomes true, never becomes true,  must remain true forever. must remain true forever. |
  |
 W W |
 |
Weak until:  has to hold at least until has to hold at least until  ; if never becomes true, ; if never becomes true,  must remain true forever. must remain true forever. |
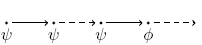  |
 M M  |
 |
Strong release: has to be true until and including the point where  first becomes true, which must hold at the current or a future position. first becomes true, which must hold at the current or a future position. |
 |
Some Equivalences
| Distributivity | ||
|---|---|---|
| X (Φ ∨ ψ) ≡ (X Φ) ∨ (X ψ) | X (Φ ∧ ψ)≡ (X Φ) ∧ (X ψ) | X (Φ U ψ)≡ (X Φ) U (X ψ) |
| F (Φ ∨ ψ) ≡ (F Φ) ∨ (F ψ) | G (Φ ∧ ψ)≡ (G Φ) ∧ (G ψ) | |
| ρ U (Φ ∨ ψ) ≡ (ρ U Φ) ∨ (ρ U ψ) | (Φ ∧ ψ) U ρ ≡ (Φ U ρ) ∧ (ψ U ρ) |
| Negation propagation | |||
|---|---|---|---|
| X is self-dual | F and G are dual | U and R are dual | W and M are dual |
| ¬X Φ ≡ X ¬Φ | ¬F Φ ≡ G ¬Φ | ¬ (Φ U ψ) ≡ (¬Φ R ¬ψ) | ¬ (Φ W ψ) ≡ (¬Φ M ¬ψ) |
| ¬G Φ ≡ F ¬Φ | ¬ (Φ R ψ) ≡ (¬Φ U ¬ψ) | ¬ (Φ M ψ) ≡ (¬Φ W ¬ψ) |
| Special Temporal properties | ||
|---|---|---|
| F Φ ≡ F F Φ | G Φ ≡ G G Φ | Φ U ψ ≡ Φ U (Φ U ψ) |
| Φ U ψ ≡ ψ ∨ ( Φ ∧ X(Φ U ψ) ) | Φ W ψ ≡ ψ ∨ ( Φ ∧ X(Φ W ψ) ) | Φ R ψ ≡ ψ ∧ (Φ ∨ X(Φ R ψ) ) |
| G Φ ≡ Φ ∧ X(G Φ) | F Φ ≡ Φ ∨ X(F Φ) |
介绍
工具支持(tool support)包括:model checking, bisimualtion,language containment, flow analysis, inequality necessary condition
模型的意义:
Patterns are successful because practitioners want to solve naturally occurring domain problems.
They don’t need the full expressiveness of the languages they use and would often prefer guidance on how best to use language features to solve commonly occuring problems.
简单来说就是模式能把时序逻辑语言封装好,使得使用者不必耗费精力去学习时序逻辑语言。
文章结构:
Section 2:描述有限状态检验的规范模式系统
Section 3:介绍调查结果
Section 4:比对Dwyer的方法与相关工作
Section 5:总结
规范模式系统(本文重点)
结构:背景知识、想法是如何被应用于属性规范的有限状态检验领域、这些pattern集合是如何被组织的以及对模式系统的近况概览
属性规范模式
作为利用专业系统设计师经验的手段,引入了设计模式。 模式旨在不仅捕获对软件设计问题的重复解决方案的描述,而且还捕获解决方案所要求的要求,满足要求的方法以及解决方案的示例。 所有这些信息都应以实践者可以理解的形式进行描述,以便他们能够识别系统中的类似需求,选择满足这些需求的模式,并实例化体现这些模式的解决方案。
对于有限状态检验,系统被建模为具有有限数量的状态的过渡系统以及在这些状态之间可能标记有事件的一组过渡。 属性规范模式是对系统的这种有限状态模型中的容许状态/事件序列的通常发生的要求的一般化描述。 属性规范模式描述了系统行为的某些方面的基本结构,并在一系列常见形式中提供了这种行为的表达。
一个模型包含了一个名称或多个名称,一个对于模型意图的精确声明,对于共同规范形式的映射,关于例子用途的例子,以及与其他模型的联系。
一些规范形式是基于事件的,而其他的规范形式是基于状态的。
在Dwyer的模型里,大写字母(P,Q,R,S)代表事件 或者 在基于事件的形式中的事件分离, 还代表在基于状态的规范里的状态公式。
每一个模型有一个作用范围(scope),这个作用范围是模式必须执行的执行程序的范围。
scope有五种:global, before, after, between, after-until。
scope通过指定 模式(pattern)的状态(state)/事件(event) 来确定。
在状态间隔范围,这个间隔是左闭右开的。因此范围包括了所有这些状态:从开始状态(starting state)开始(begin)并且持续(up to),但是不包括结束状态(ending state)。
不同的形式规范有不同的语义和表现力。一个可以很容易地在一种形式里表达出来的属性,可能不能很自然地、甚至不可能在另一种形式里很精确地描述。
规范模式系统
Dwyer为有限状态检验工具开发了一个关于属性规范的模式系统。模式系统是组织成一个或多个层次结构的一组模式,在相关模式之间建立连接以便于浏览。
在定义规范形式时,人们试图给出一小组独立的概念,从这一小组独立的概念中可以构建一大类规范。但是对于规范模式的集合而言,Dwyer既不想给出可以生成有用规范的最小集合,也不会提供完整的规范列表。模式仅作为属性规范出现在系统中。
模式
对于模式的具体说明可以在这里看到。下面给出一些简短说明:(在描述中,为了简洁起见,Dwyer使用短语“给定的状态/事件发生”来表示“给定的状态公式是true的状态/来自给定的 事件分离(disjunction of events) 的事件发生”。)
Absence:给定的状态/事件在一个范围内没有发生
Existence:给定的状态/事件在一个范围内有发生
Bounded Existence:给定的状态/事件在一个范围内必须发生k次。该模式的变体至少指定k次出现,并且至多指定k次出现的状态/事件。
Universality:给定的状态/事件发生在整个范围内(occurs throughout a scope)
Precedence:在一个范围内,状态/事件P必须总是在状态/事件Q之前(或者说,状态/事件P必须总是优先于状态/事件Q)
Response:在一个范围内,状态/事件P必须总是被状态/事件Q跟随(或者说,状态/事件P发生之后才能发生状态/事件Q)
Chain Precedence:状态/事件队列P1,P2,...,Pn 必须总是优先于(be preceded by)状态/事件队列Q1,Q2,...,Qn。这个模式是Precedence模式的概括(generalization)。
Chain Response:状态/事件队列P1,P2,...,Pn 发生之后才能发生 (be followedby)状态/事件队列Q1,Q2,...,Qn。这个模式是Response模式的概括(generalization)。它可以用来表达有界的FIFO关系
组织(organization)
组织模式最有效的方法是一个基于这些模式语义的等级制度。
比如说,有些模式要求状态/事件发生或者不发生(比如Absence模式),而另外的模式则约束了状态/事件的顺序(比如Response模式)
Dwyer提供了一个关于模式注释的集合,解释了如何组合and/or 去改变模式。比如说,模式模板通常由单个事件或状态公式来参数化。但是在一些情况下,Dwyer允许状态/事件模式被替换进模板中。
属性模式:occurrence,order
occurrence:Absence,Existence,Bounded Existence,Universality
order:Precedence,Response,Chain Precedence,Chain Response
属性规范的调查
数据收集
Dwyer收集了500份specification样例,发现大部分都属于少数相似的类别。
样例来源:
-
文献中的检验文件
-
别的写了或者收集了规范的文件
-
学生做的项目:来自第一Dwyer的毕业生的有限状态验证课程。
总共从至少35个不同的来源收集了555个规范(specification)。大多数规范,Dwyer都用一种特定的规范模式建立了一个对于需求的表达式。而对于其中许多规范,Dwyer还有一个关于需求的非正式描述。这些规范来自各种各样的应用领域:硬件协议, 通信协议, GUI,控制系统, 抽象数据类型,航空电子设备,操作系统, 分散式对象系统, 以及数据库。这些规范的完整描述可以在规范模式看到。
在大多数情况下,正常的规范版本是一个 映射了规范模式/范围的 模板的一个实例(an instantiation of a template mapping for a specific pattern/scope);而这些规范是哪个领域的并不重要。
如果找不到哪怕是微小的匹配,Dwyer会更仔细地查看规范,并在以下情况仍视为匹配:
-
该规范与Dwyer的模板映射之一的实例化在形式上(formally)等价。比如LTL形式的¬◇P等价于□¬P,这是Dwyer对于P的(全局)absence的映射
-
该规范可以从Dwyer的一个模式中使用参数替换获得。对于一些模式/范围而言,将时态公式替换为模板是安全的(何时可以这样操作的指导见于模式注释(pattern note))。
-
该规范是Dwyer的一个模式的已知变体。比如左闭右开与左开右闭。
-
该规范是Dwyer的一个模式的一种新变体。
-
该规范的形式表达式完全错误,并且正确的规范是Dwyer的一个模式的一个实例
对于每个规范,Dwyer记录了这些信息(如果有的话):
- 需求(requirement):一个对于需求的零散(prose)描述。
- 模式(pattern):Dwyer用于确定这个需求 的模式是一个实例(如果有的话)。
- 范围(scope):模式的范围。
- 参数(parameters):提供给模板的参数注释。(比如,命题阵列arrays of propositions,嵌套时间公式nested temporal formulae)
- 映射(mapping):属性到形式规范语言(LTL, CTL, QREs, GIL, INCA)的映射。大部分样例只有一种映射。
- 来源(source):样例来源( 人,引用...)
- 领域(domain):样例来源的应用领域
- 注释(note):样例中任何的额外信息
一个例子:
REQUIREXNT: When a server requests its registration in the ROT, it will eventually be registered.
PATTERN: Response
SCOPE: Global
PARAMIZTERS:Propositions (boolean vector)
LTL: [](RequestedRegisterImpl[i] -> <>ServerRegistered[i])
NOTE: this is replicated for all modeled servers
SOURCE: Gregory Duval \cite{duval:98}, RI, pp. 46
DOMAIN: Distributed Object System
结果
从结果上看,模式出现的频率在排序后下降得很快,这就引出了一个关于size的问题:模式系统里应该有多少模式?系统中的模式越多,一个匹配就越容易找到。在另一方面,系统应该足够小以便于浏览。添加一些只匹配很少规范的模式可能不能抵消模式系统size的轻微增加,即有可能得不偿失。
在表中,Dwyer能看到,大多数样例(80%)使用了global范围。并且,注意到几乎所有使用了non-global范围的样例都是Absence,University, 或者Existence 的实例。这三个模式是概念上最简单的。对于global范围,它们映射到简单的时间逻辑运算。
现在看看合Dwyer以及学生("Dwyer")写的规范(304个)与"别人"写的规范(251个)的区别:四个最常见的模式(Response, Universality, Absence, UNKNOWN(也就是无法识别的))是一样的。而其余的模式是不一样的,但是由于数据量较小,所以可能是误差。有一个不同的是,“Dwyer”写下更多带有non-global范围的规范,虽然“Dwyer”的绝大部分规范也使用了global范围。有趣的是,“Dwyer”比“别人”写下更多模式系统之外的规范。
另一个有趣的问题是:模式系统是否会影响人们编写的规范?有限状态验证通常被用于检查重要的需求,但是将要被检查的确切需求选择(exact choice of requirements to be checked),以及这些需求在模型方面被表达的方式,通常是留给分析师的。在给定一个模式系统来协助制定属性映射的情况下,分析师可能更倾向于使用更复杂的模式 and/ or 范围。为了调查这个,Dwyer采用了“Dwyer”的一组规范,并且在Dwyer开发模式系统之前编写的165个规范,以及开发之后编写的139个规范。
在这次比较中,区别更加明显:一些更复杂的模式(比如chains)只在引入模式系统后才出现。在开发完模式系统之后编写的规范中,更多规范使用了non-global范围(33% vs. 5%),并且那些后来的规范更均匀(尽管不是统一的)分布在不同的模式上。同时,注意到在开发完模式系统之后编写的所有规范都符合其中一种模式。
所以,用于有限状态验证的属性规范的模式系统有着很大的潜力,它显示出绝大部分规范都落在少数的分类中。为了表明该系统实际上有用,需要回答几个更难的问题,其中包括:
- 模式是否有助于学习规范形式?
- 模式是否允许更快地写出规范?
- 从模式生成的规范是否更可能是正确的?
解答这些问题还是需要实验数据。到目前为止,本文Dwyer只有一些证据支持他们的观点,主要来自本文一作在硕士级软件工程课程中教授有限状态验证课程的经验。
相关工作
传统上,规范形式化是以最小的一组操作符集来表示的,这是为了简化它们的语义定义。 然后根据这些操作符来定义其他操作符,比如,□P = ¬◇¬P,所以只有几个基元需要正式定义。这种形式的用户宁愿编写比这更高级别的规范,所以许多形式提供内置的更高级别的操作符或抽象。Dwyer的模式系统支持一套通用的,但固定的形式化规范抽象,不过这个形式缺乏对定义抽象的明确支持。
关于开发者可能或者确实写的规范类别的研究很少。 Manna和Pnueli [17]从理论角度解决了这个问题,提出了LTL公式的句法分类,它完全描述了人们可能在LTL中编写的可能规范的空间。他们的规范分类包括比Dwyer的模式更广泛的类别。因此,Dwyer的大多数模式很容易按其分类进行分类:具有global范围的precedence,absence和universal模式都是safety属性,具有global范围的existence模式是guarantee属性,global范围的response模式是response属性。Dwyerk-bounded existence模式与它们的k-bounded overtaking性质(这是一种safety属性)非常相似。因为chain模式和complex范围,对语法类别的映射变得更加困难(由于定义类别的规范形式的性质)。与这项工作相反,Dwyer工作的目标是对实践中最频繁出现的规范类别进行建设性描述。
他们声称,时间逻辑的一般理论很少需要处理并发程序的最重要,最常见,最正确的属性。他们定义了一个处理invariance属性(归入most universal 和absence模式),response属性(归入response模式)和precedence属性(归入precedence和bounded existence并且类似于chain模式)的受限证明系统(restricted proof-system)。它们的precedence属性也包含universal和absence模式的after-until范围版本。Dwyer在Dwyer中提供的数据支持了Manna和Pnueli关于常见属性的直觉,因为Dwyer发现absence,universal和response模式构成了Dwyer调查中的大部分属性。
结论
Dwyer认为在编写正式规范时定义和使用高级抽象是使自动化形式化方法(特别是有限状态验证工具)更加可用的重要因素。Dwyer的规范模式系统为形式化提供了一组通用的高级规范抽象,这些抽象不直接支持这些抽象的定义。Dwyer描述了一个更新的模式系统,Dwyer为有限状态验证中的属性规范开发了一个更新的模式系统,并收集了大量规范样本,这些规范说明大多数人编写的属性规范都是该系统中模式的实例。
目前Dwyer正在探索几个方向来进一步研究规范模式。
Dwyer正在努力定义模式来简化在CTL中编写一类假设-保证(assume-guarantee)属性。在LTL中编写这样的规范非常简单;但在CTL中,这些属性可能非常难以表达。Dwyer正在研究基于模式为属性规范定义语言的好处,提供自动化支持,将用该语言表达的属性编译为特定的形式,并检查模式替换的合法性。
Dwyer正在研究检查 以多种形式表达的模式映射的 一致性的方法。例如,虽然CTL和LTL通常不共同表达,但Dwyer所有的CTL和LTL映射都位于CTL *的全路径片段(all-paths fragment)中;因此Dwyer可能能够正式证明这些映射的等价性。
Dwyer将模式系统视为一个动态实体,它将通过有限状态验证技术的开发人员和用户的社区的对话和批判性评论成长。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号