排列组合

一·不定方程解的个数

例：一个商场有m种颜色的小球，每种小球足够多，在这m种小球中挑选n个小球的选法有多少？

一道纯纯的数学题对吧。

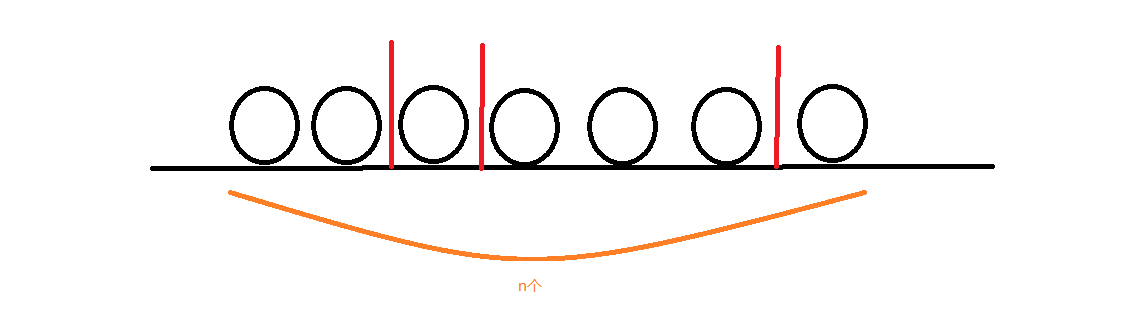
由题目，我们可以知道\(\sum_{i=1}^n a[i]=n\)，我们将n分成若干个1

1.解都为正整数

挑选不同颜色的小球，可理解为在这一串1里插入m-1个隔板，每个被隔开的区间即为各种颜色的各自的数量，如上图所示
所以答案为\(C_{n-1}^{m-1}\),即从n-1个间隔中插入m-1个隔板

2.解都为非负整数

我们要注意的是，某一种颜色的小球可以为0,即多个隔板可以放在同一个位置，而这种特殊情况，可以通过加1的方法消除这种情况，即每个颜色的区间里多加一个1。以下为说明：
\(\sum_{i=1}^n a[i]=n\)可以转化为\(\sum_{i=1}^n b[i]=n+m\),其中b[i]=a[i]+1。这两者是等价的对吧。所以对于第二个式子的解的个数即为答案，那么又通过1中所证，答案即为\(C^{m-1}_{n+m-1}\)

二.错位排序

1.什么是错位排序

对于一个数列，将其中的数打乱，使任意位置上的数不是原来的数。
这里先给出方案数为\(D_n=\)(n-1)*(\(D_{n-1}\)+\(D_{n-2}\))。
注：D数组为错位排序的方案数

2.证明

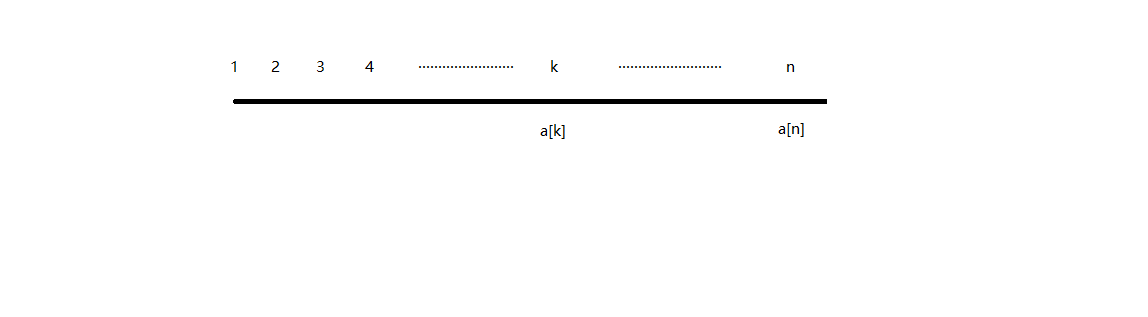
首先，对于n这个点，可以放到其他n-1个点里，假定这个点为k，接下来分类讨论

(1)k在n这个位置

此时即为\(D_{n-2}\),因为有两个位置都已经固定下来了

（2）k不在n这个位置

只有1个点是固定下来的，所以答案为\(D_{n-1}\)
那么根据乘法原理与加法原理得出我们要证的式子，完毕