KD树

KD树

1. 概述

KD树是一种查询索引结构，广泛应用于数据库索引中。从概念的角度讲，它是一种高纬数据的快速查询结构，本文首先介绍1维数据的索引查询，然后介绍2维KD树的创建和查询

2. 1维数据的查询

假设在数据库的表格T中存储了学生的语文成绩chinese、数学成绩math、英语成绩english，如果要查询语文成绩介于30～93分的学生，如何处理？假设学生数量为N，如果顺序查询，则其时间复杂度为O(N)，当学生规模很大时，其效率显然很低，如果使用平衡二叉树，则其时间复杂度为O(logN)，能极大地提高查询效率。平衡二叉树示意图为：

 

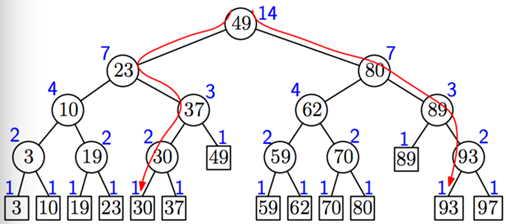
平衡二叉树示意图

对于1维数据的查询，使用平衡二叉树建立索引即可。如果现在将查询条件变为：语文成绩介于30～93，数学成绩结余30～90，又该如何处理呢？

如果分别使用平衡二叉树对语文成绩和数学成绩建立索引，则需要先在语文成绩中查询得到集合S₁，再在数学成绩中查询得到集合S₂，然后计算S₁和S₂的交集，若|S₁|=m,|S₂|=n，则其时间复杂度为O(m*n)，有没有更好的办法呢？

3. KD树

针对多维数据索引，是否也存在类似的一维的索引方法呢？先看2维数据的集合示意图：

2维数据示意图

如果先根据语文成绩，将所有人的成绩分成两半，其中一半的语文成绩<=c₁，另一半的语文成绩>c₁，分别得到集合S₁,S₂;然后针对S₁，根据数学成绩分为两半，其中一半的数学成绩<=m₁,另一半的数学成绩>m₁，分别得到S₃,S₄，针对S₂，根据数学成绩分为两半，其中一半的数学成绩<=m₂,另一半的数学成绩>m₂，分别得到S₅,S₆；再根据语文成绩分别对S₃,S₄，S₅,S₆继续执行类似划分得到更小的集合，然后再在更小的集合上根据数学成绩继续,...

上面描述的就是构建KD树的基本思路，其构建后的KD树如下图所示：

 

KD树示意图

如图所示，l1左边都是语文成绩低于45分，l1右边都是语文成绩高于45分的；l2下方都是语文成绩低于45分且数学成绩低于50分的，l2上方都是语文成绩低于45分且数学成绩高于50分的，后面以此类推。下面的图示，更清晰地表示了KD树的结构及其对应的二叉树：

 

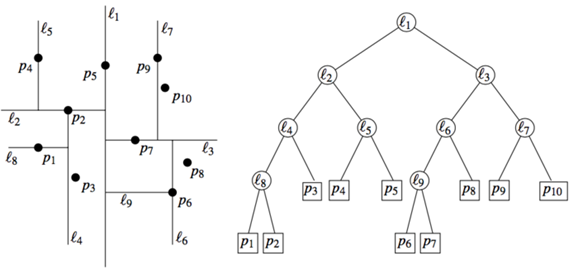
KD树及对应的二叉树

在了解了KD树的基本原理后，剩下的工作就是如何构建KD树以及如何在KD树上查询了。

3.1 KD树构建算法

相对而言，构建KD树是针对高维数据，需要针对每一维都进行二分，针对二维数据的KD树构建算法如下图所示：

 

KD树构建算法

其中的P表示待构建的元素集合，depth表示当前是KD树的第几层，如果depth是偶数，通过纵向线对集合进行划分；如果depth是奇数，通过横向线进行划分（3～5行）；第6、7行递归进行KD树中子树的构建。

算法时间复杂度为：O(nlogn)，感兴趣的同学可以写出递推公式公式进行推到，算法导论中专门讲了这个递推公式。

3.2 KD树查询算法

在构建了KD树的基础上，如何进行查询其实是一个相对简单的问题了，在这里需要注意的是，在KD树中每一层划分所依据的是哪一维的数据，其它的根二叉树其实没有差别。KD树查询算法如下图所示：

查询算法

算法的v表示KD树中当前搜索的子树，R表示是一个高维数据的区域，区域的概念下图所示：

 

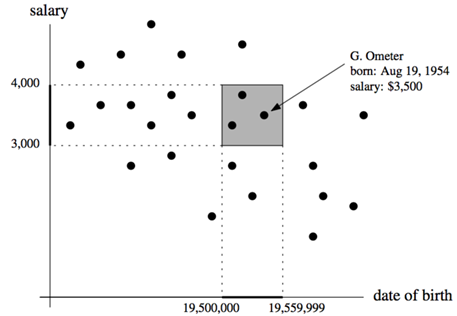
区域示意图

如果v是叶子结点且属于区域R，则直接返回（第1行）；如果v是非叶子结点，则比较R与v的左子树lc(v)是否有交集，如果有且lc(v)完全被R覆盖，则lc(v)是所查询结果的一部分，如果不是完全覆盖，则递归查询lc(v)；对右子树也是类似的操作。算法的时间复杂度为：O(sqrt(n) + k)，其中k是最后的结果中元素的个数，其递推公式公式为：

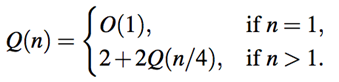
KD树查询递推公式

上述算法中的二维也可升级为3维，其思维方式与从1维升级到2维一致，相应的构建算法和查询算法也与2维的一致，感兴趣的童鞋可以分析相应算法的时间复杂度。

4. 小结

本文以从1维数据索引跳变到2维数据索引的方式，引出了KD树，并介绍了KD树的构建与索引查询算法。KD树主要应用在高维数据索引，特别是空间数据库的索引，x和y分别表示经度和纬度，能较好的处理空间上的查询效率问题，如果在x和y再加一个时间维度，也能较好地处理时空数据索引查询。

 

 

k-d tree算法原理及实现

k-d tree即k-dimensional tree，常用来作空间划分及近邻搜索，是二叉空间划分树的一个特例。通常，对于维度为k，数据点数为N的数据集，k-d tree适用于N≫2k的情形。
1）k-d tree算法原理
k-d tree是每个节点均为k维数值点的二叉树，其上的每个节点代表一个超平面，该超平面垂直于当前划分维度的坐标轴，并在该维度上将空间划分为两部分，一部分在其左子树，另一部分在其右子树。即若当前节点的划分维度为d，其左子树上所有点在d维的坐标值均小于当前值，右子树上所有点在d维的坐标值均大于等于当前值，本定义对其任意子节点均成立。
1.1）树的构建
一个平衡的k-d tree，其所有叶子节点到根节点的距离近似相等。但一个平衡的k-d tree对最近邻搜索、空间搜索等应用场景并非是最优的。
常规的k-d tree的构建过程为：循环依序取数据点的各维度来作为切分维度，取数据点在该维度的中值作为切分超平面，将中值左侧的数据点挂在其左子树，将中值右侧的数据点挂在其右子树。递归处理其子树，直至所有数据点挂载完毕。
a）切分维度选择优化
构建开始前，对比数据点在各维度的分布情况，数据点在某一维度坐标值的方差越大分布越分散，方差越小分布越集中。从方差大的维度开始切分可以取得很好的切分效果及平衡性。
b）中值选择优化
第一种，算法开始前，对原始数据点在所有维度进行一次排序，存储下来，然后在后续的中值选择中，无须每次都对其子集进行排序，提升了性能。
第二种，从原始数据点中随机选择固定数目的点，然后对其进行排序，每次从这些样本点中取中值，来作为分割超平面。该方式在实践中被证明可以取得很好性能及很好的平衡性。
本文采用常规的构建方式，以二维平面点(x,y)的集合(2,3)，(5,4)，(9,6)，(4,7)，(8,1)，(7,2)为例结合下图来说明k-d tree的构建过程。
a）构建根节点时，此时的切分维度为x，如上点集合在x维从小到大排序为(2,3)，(4,7)，(5,4)，(7,2)，(8,1)，(9,6)；其中值为(7,2)。（注：2,4,5,7,8,9在数学中的中值为(5 + 7)/2=6，但因该算法的中值需在点集合之内，所以本文中值计算用的是len(points)//2=3, points[3]=(7,2)）
b）(2,3)，(4,7)，(5,4)挂在(7,2)节点的左子树，(8,1)，(9,6)挂在(7,2)节点的右子树。
c）构建(7,2)节点的左子树时，点集合(2,3)，(4,7)，(5,4)此时的切分维度为y，中值为(5,4)作为分割平面，(2,3)挂在其左子树，(4,7)挂在其右子树。
d）构建(7,2)节点的右子树时，点集合(8,1)，(9,6)此时的切分维度也为y，中值为(9,6)作为分割平面，(8,1)挂在其左子树。至此k-d tree构建完成。

上述的构建过程结合下图可以看出，构建一个k-d tree即是将一个二维平面逐步划分的过程。

我们还可以结合下图（该图引自维基百科），从三维空间来看一下k-d tree的构建及空间划分过程。
首先，边框为红色的竖直平面将整个空间划分为两部分，此两部分又分别被边框为绿色的水平平面划分为上下两部分。最后此4个子空间又分别被边框为蓝色的竖直平面分割为两部分，变为8个子空间，此8个子空间即为叶子节点。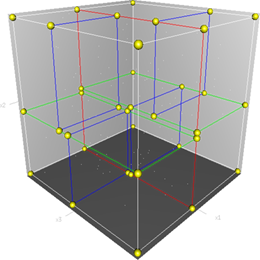

如下为k-d tree的构建代码：

1. def kd_tree(points, depth):
2.     if 0 == len(points):
3.         return None
4.     cutting_dim = depth % len(points[0])
5.     medium_index = len(points) // 2
6.     points.sort(key=itemgetter(cutting_dim))
7.     node = Node(points[medium_index])
8.     node.left = kd_tree(points[:medium_index], depth + 1)
9.     node.right = kd_tree(points[medium_index + 1:], depth + 1)
10.     return node

1.2）寻找d维最小坐标值点
a）若当前节点的切分维度是d
因其右子树节点均大于等于当前节点在d维的坐标值，所以可以忽略其右子树，仅在其左子树进行搜索。若无左子树，当前节点即是最小坐标值节点。
b）若当前节点的切分维度不是d
需在其左子树与右子树分别进行递归搜索。
如下为寻找d维最小坐标值点代码：

1. def findmin(n, depth, cutting_dim, min):
2.     if min is None:
3.         min = n.location
4.     if n is None:
5.         return min
6.     current_cutting_dim = depth % len(min)
7.     if n.location[cutting_dim] < min[cutting_dim]:
8.         min = n.location
9.     if cutting_dim == current_cutting_dim:
10.             return findmin(n.left, depth + 1, cutting_dim, min)
11.     else:
12.         leftmin = findmin(n.left, depth + 1, cutting_dim, min)
13.         rightmin = findmin(n.right, depth + 1, cutting_dim, min)
14.         if leftmin[cutting_dim] > rightmin[cutting_dim]:
15.             return rightmin
16.         else:
17.             return leftmin

1.3）新增节点
从根节点出发，若待插入节点在当前节点切分维度的坐标值小于当前节点在该维度的坐标值时，在其左子树插入；若大于等于当前节点在该维度的坐标值时，在其右子树插入。递归遍历，直至叶子节点。
如下为新增节点代码：

1. def insert(n, point, depth):
2.     if n is None:
3.         return Node(point)
4.     cutting_dim = depth % len(point)
5.     if point[cutting_dim] < n.location[cutting_dim]:
6.         if n.left is None:
7.             n.left = Node(point)
8.         else:
9.             insert(n.left, point, depth + 1)
10.     else:
11.         if n.right is None:
12.             n.right = Node(point)
13.         else:
14.             insert(n.right, point, depth + 1)

多次新增节点可能引起树的不平衡。不平衡性超过某一阈值时，需进行再平衡。
1.4）删除节点
最简单的方法是将待删节点的所有子节点组成一个新的集合，然后对其进行重新构建。将构建好的子树挂载到被删节点即可。此方法性能不佳，下面考虑优化后的算法。
假设待删节点T的切分维度为x，下面根据待删节点的几类不同情形进行考虑。
a）无子树
本身为叶子节点，直接删除。
b）有右子树
在T.right寻找x切分维度最小的节点p，然后替换被删节点T；递归处理删除节点p。
c）无右子树有左子树
在T.left寻找x切分维度最小的节点p，即p=findmin(T.left, cutting-dim=x)，然后用节点p替换被删节点T；将原T.left作为p.right；递归处理删除节点p。
（之所以未采用findmax(T.left, cutting-dim=x)节点来替换被删节点，是由于原被删节点的左子树节点存在x维度最大值相等的情形，这样就破坏了左子树在x分割维度的坐标需小于其根节点的定义）
如下为删除节点代码：

1. def delete(n, point, depth):
2.     cutting_dim = depth % len(point)
3.     if n.location == point:
4.         if n.right is not None:
5.             n.location = findmin(n.right, depth + 1, cutting_dim, None)
6.             delete(n.right, n.location, depth + 1)
7.         elif n.left is not None:
8.             n.location = findmin(n.left, depth + 1)
9.             delete(n.left, n.location, depth + 1)
10.             n.right = n.left
11.             n.left = None
12.         else:
13.             n = None
14.     else:
15.         if point[cutting_dim] < n.location[cutting_dim]:
16.             delete(n.left, point, depth + 1)
17.         else:
18.             delete(n.right, point, depth + 1)

2）最近邻搜索
给定点p，查询数据集中与其距离最近点的过程即为最近邻搜索。
如在上文构建好的k-d tree上搜索(3,5)的最近邻时，本文结合如下左右两图对二维空间的最近邻搜索过程作分析。
a）首先从根节点(7,2)出发，将当前最近邻设为(7,2)，对该k-d tree作深度优先遍历。以(3,5)为圆心，其到(7,2)的距离为半径画圆（多维空间为超球面），可以看出(8,1)右侧的区域与该圆不相交，所以(8,1)的右子树全部忽略。
b）接着走到(7,2)左子树根节点(5,4)，与原最近邻对比距离后，更新当前最近邻为(5,4)。以(3,5)为圆心，其到(5,4)的距离为半径画圆，发现(7,2)右侧的区域与该圆不相交，忽略该侧所有节点，这样(7,2)的整个右子树被标记为已忽略。
c）遍历完(5,4)的左右叶子节点，发现与当前最优距离相等，不更新最近邻。所以(3,5)的最近邻为(5,4)。

如下为最近邻搜索代码：
3）复杂度分析

操作	平均复杂度	最坏复杂度
新增节点	O(logn)	O(n)
删除节点	O(logn)	O(n)
最近邻搜索	O(logn)	O(n)

4）scikit-learn使用
scikit-learn是一个实用的机器学习类库，其有KDTree的实现。如下例子为直观展示，仅构建了一个二维空间的k-d tree，然后对其作k近邻搜索及指定半径的范围搜索。多维空间的检索，调用方式与此例相差无多。

1. #!/usr/bin/python
2. # -*- coding: UTF-8 -*-
3. import numpy as np
4. from matplotlib import pyplot as plt
5. from matplotlib.patches import Circle
6. from sklearn.neighbors import KDTree
8. np.random.seed(0)
9. points = np.random.random((100, 2))
10. tree = KDTree(points)
11. point = points[0]
13. # kNN
14. dists, indices = tree.query([point], k=3)
15. print(dists, indices)
17. # query radius
18. indices = tree.query_radius([point], r=0.2)
19. print(indices)
21. fig = plt.figure()
22. ax = fig.add_subplot(111, aspect='equal')
23. ax.add_patch(Circle(point, 0.2, color='r', fill=False))
24. X, Y = [p[0] for p in points], [p[1] for p in points]
25. plt.scatter(X, Y)
26. plt.scatter([point[0]], [point[1]], c='r')
27. plt.show()