关于素数的一些渐近公式

来统计一些关于素数的渐近公式。

鉴定为没什么用的文章。

一、素数个数

记 \(\pi(n)\) 为 \(1\) 到 \(n\) 中素数的个数，那么有：

\[\Huge \pi(n)\sim \frac{n}{\ln n} \]

二、前缀最大约数个数

这个其实有点爆论。

记 \(d(n)\) 为 \(n\) 的约数个数，记 \(\max d(n)\) 为 \(1\) 到 \(n\) 中最大的 \(d(n)\) 的值。

那么有：

\[\Huge \max d(n) \sim n^\frac{1.066}{\ln \ln n} \]

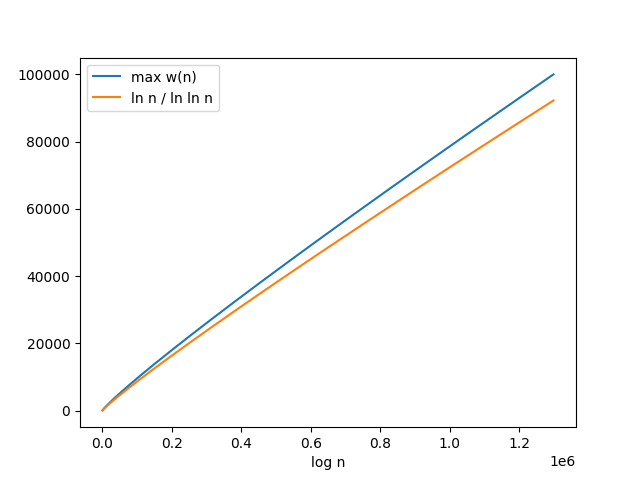
三、前缀最大不同质因子个数

记 \(\omega (n)\) 为 \(n\) 的不同质因子个数，记 \(\max \omega(n)\) 为 \(1\) 到 \(n\) 中最大的 \(\omega(n)\) 的值。

那么有：

\[\Huge \max \omega(n)\sim \frac{\ln n}{\ln \ln n} \]

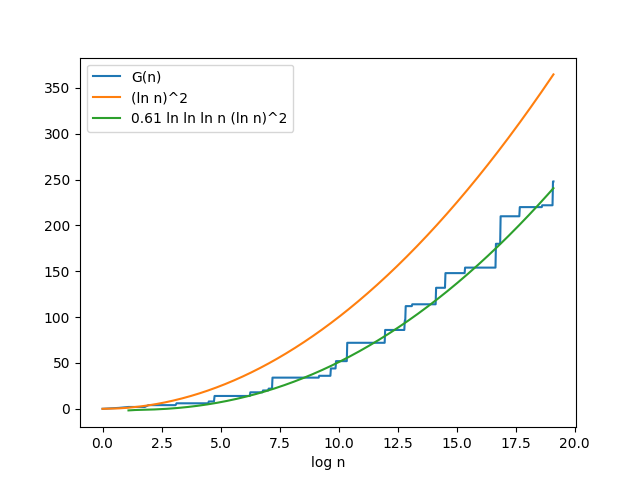
四、前缀最大素数间隔

令 \(G(x)=\max_{p_n \le x}p_{n+1}-p_n\)。

那么根据素数密度，并把素数分布当作随机撒点，可以得出 \(G(x)\sim (\log x)^2\)。

但是有一种比较爆论的渐进：

\[\Huge G(n)\sim 0.61 \ln \ln \ln n (\ln n)^2 \]