2025-1-1 / 2025-1-2 做题笔记

2025-1-1 / 2025-1-2 做题笔记

持续更新中……

目录

CF1534H - Lost Nodes

首先设 \(ans_i\) 为 \(f=i\) 中的最坏情况下的最小询问数，第一问就是 \(\max ans_i\)，接下来考虑求解 \(ans_i\) 也就是第二问。

不难发现第一步应该是确定在根为 \(f\) 下，\(a\) 和 \(b\) 在哪颗子树里面，问出子树后继续递归是什么子树，所以直接设初步 dp，\(dp_u\) 为在根为 \(f\) 下，确定点在 \(u\) 里中的哪颗子树里，或者在 \(u\) 上的代价。

对于一个叶子 \(u\)，需要检查一遍有没有点，代价为 \(1\)。

对于普通节点 \(u\)，对于一个儿子 \(v\)，需要检查点是否在 \(v\) 子树内，这需要 \(1\) 的代价，但是不管在 \(v\) 里询问什么，都可以得出点是否在 \(v\) 子树内，所以直接去根据 \(v\) 的最优策略问，如果没有就直接退出，所以对于第一个子树代价即为 \(dp_v\)，若在子树 \(v\) 里没有点，这是浪费了一个代价，并且要去问下一个子树，以此类推，那么转移即为：

\[dp_u=\max_{i=0}^{sz_u-1}dp_{v_i}+i \]

要最小化这个东西，即为按照从大到小排序 \(dp_{v_i}\)。

对于 \(ans_u\)，最多需要找到两个子树，那么最坏的代价为 \(\max_{0\le i<j<sz_u}dp_i+dp_j+j-1\)，最小可以做到 \(dp_{v_0}+\max_{i=1}^{sz_u-1}dp_{v_i}+i-1\)，其中 \(v_i\) 是通过将 \(dp_{v_i}\) 从大到小排完序后的结果。

上述都是对于根固定的情况，换根 dp 即可得出所有的 \(ans_i\)。

对于第二问，直接根据转移的方式，直接模拟即可。

时间复杂度 \(O(n \log n)\)。

ケロシの代码 
const int N = 1e5 + 5;
int n, dp[N], F[N];
int a[N], b[N], f[N], g[N], t[N], len;
int fi[N], ne[N << 1], to[N << 1], ecnt;
vector<int> e[N];
void add(int u, int v) {
	ne[++ ecnt] = fi[u];
	to[ecnt] = v;
	fi[u] = ecnt;
}
void dfs1(int u, int fa) {
	for(int i = fi[u]; i; i = ne[i]) {
		int v = to[i];
		if(v == fa) continue;
		dfs1(v, u);
	}
	len = 0;
	for(int i = fi[u]; i; i = ne[i]) {
		int v = to[i];
		if(v == fa) continue;
		a[++ len] = dp[v];
	}
	sort(a + 1, a + len + 1);
	reverse(a + 1, a + len + 1);
	dp[u] = 1;
	FOR(i, 1, len) chmax(dp[u], a[i] + i - 1);
}
void dfs2(int u, int fa, int f0) {
	len = 0;
	for(int i = fi[u]; i; i = ne[i]) {
		int v = to[i];
		if(v == fa) continue;
		a[++ len] = dp[v];
	}
	a[++ len] = f0;
	sort(a + 1, a + len + 1);
	reverse(a + 1, a + len + 1);
	F[u] = 1;
	FOR(i, 2, len) chmax(F[u], a[1] + a[i] + i - 2);
	FOR(i, 1, len) f[i] = max(f[i - 1], a[i] + i - 1);
	g[len + 1] = 0;
	ROF(i, len, 1) g[i] = max(g[i + 1], a[i] + i - 1);
	FOR(i, 1, len) b[a[i]] = i;
	for(int i = fi[u]; i; i = ne[i]) {
		int v = to[i];
		if(v == fa) continue;
		int pos = b[dp[v]];
		t[v] = max({1, f[pos - 1], g[pos + 1] - 1});
	}
	for(int i = fi[u]; i; i = ne[i]) {
		int v = to[i];
		if(v == fa) continue;
		dfs2(v, u, t[v]);
	}
}
void dfs0(int u, int fa) {
	for(int i = fi[u]; i; i = ne[i]) {
		int v = to[i];
		if(v == fa) continue;
		dfs0(v, u);
	}
	for(int i = fi[u]; i; i = ne[i]) {
		int v = to[i];
		if(v == fa) continue;
		e[u].push_back(v);
	}
	sort(e[u].begin(), e[u].end(), [&] (int x, int y) {
		return dp[x] > dp[y];
	});
}
int query(int u) {
	cout << "? " << u << endl << flush;
	int v; cin >> v;
	return v;
}
int dfs(int u) {
	if(e[u].empty()) return query(u);
	for(int v : e[u]) {
		int val = dfs(v);
		if(val != u) return val;
	}
	return u;
}
void solve() {
	cin >> n;
	if(n == 1) {
		cout << 0 << endl << flush;
		int x; cin >> x;
		cout << "! " << 1 << " " << 1 << endl << flush;
		return;
	}
	REP(_, n - 1) {
		int u, v;
		cin >> u >> v;
		add(u, v), add(v, u);
	}
	dfs1(1, 0);
	dfs2(1, 0, 0);
	int ans = 0;
	FOR(i, 1, n) chmax(ans, F[i]);
	cout << ans << endl << flush;
	int rt; cin >> rt;
	int A = rt, B = rt;
	dfs1(rt, 0);
	dfs0(rt, 0);
	for(int v : e[rt]) {
		int val = dfs(v);
		if(val != rt) {
			if(A == rt) {
				A = val;
			}
			else {
				B = val;
				break;
			}
		}
	}
	cout << "! " << A << " " << B << endl << flush;
}

CF1510B - Button Lock

首先考虑建出单向图，对于点 \(S\) 和 点 \(T\)，若 \(S \subset T\)，则连一条 \(S\) 到 \(T\) 的边。因为有重置操作，所以再搞一个根连向所有点。

不难发现接下来就变为了一个最小路径覆盖问题，需要用从根开始的链覆盖所有的点，一条链的代价为根到链底所需的代价。

对于链覆盖问题，考虑网路流，因为有不同的代价权，考虑建费用流，类似普通最小链覆盖，把原图拆成二分图，每个点有入点 \(in(u)\) 和出点 \(out(u)\)。

若原图上 \(u\) 到 \(v\) 有边，则在费用流上建 \(in(u) \to out(v)\)，流量为 \(1\)，费用为 \(-w(u)\)，意义是通过走 \(u\) 到 \(v\)，省去了点 \(u\) 的代价。

因为一个点不可能省或被省去两次，且原图本来就是一个闭包，所以直接再建出原点 \(S\) 和汇点 \(T\)，连 \(S \to in(u)\) 和 \(out(u) \to T\)，流量为 \(1\)，费用为 \(0\)。

但是直接跑费用流可能跑不过，考虑到费用的范围很小，根据费用流每次增广最短路，所以直接从小到大枚举费用加边，每次跑一遍最大流即可。

时间复杂度 \(O(d2^d\sqrt{3^d})\)。

ケロシの代码 
namespace Dinic {
	const int N = 3e3 + 5;
	const int M = 1e6 + 5;
	const int INF = 0x3f3f3f3f;
	struct Edge {
		int ne, to, ew;
	} e[M];
	int S, T; 
	int fi[N], c[N], ecnt;
	int d[N];
	void init() {
		memset(fi, 0, sizeof fi);
		ecnt = 1;
	}
	void add(int u, int v, int w) {
		e[++ ecnt] = {fi[u], v, w};
		fi[u] = ecnt;
		e[++ ecnt] = {fi[v], u, 0};
		fi[v] = ecnt;
	}
	bool bfs() {
		memset(d, 0x3f, sizeof d);
		queue<int> q;
		d[S] = 0; q.push(S);
		while(! q.empty()) {
			int u = q.front();
			q.pop();
			for(int i = fi[u]; i; i = e[i].ne) if(e[i].ew) {
				int v = e[i].to;
				if(d[v] == INF) {
					d[v] = d[u] + 1;
					q.push(v);
				}
			}
		}
		return d[T] != INF;
	}
	int dfs(int u, int w) {
		if(u == T || ! w) return w;
		int res = 0;
		for(int & i = c[u]; i; i = e[i].ne) {
			int v = e[i].to;
			if(d[v] != d[u] + 1) continue;
			int val = dfs(v, min(e[i].ew, w));
			e[i].ew -= val;
			e[i ^ 1].ew += val;
			w -= val;
			res += val;
			if(! w) return res;
		}
		return res;
	}
	int dinic(int _S, int _T) {
		S = _S, T = _T;
		int res = 0;
		while(bfs()) {
			memcpy(c, fi, sizeof c);
			res += dfs(S, INF);
		}
		return res;
	}
}
const int N = 1.1e3 + 5;
int d, n, a[N], vis[N];
vector<PII> e[N];
void add(int u, int v, int w) {
	e[w].push_back({u, v});
}
void print(int x, int y) {
	REP(i, d) if((x >> i & 1) != (y >> i & 1))
		cout << i << " ";
}
void dfs(int u) {
	vis[u] = 1;
	for(int i = Dinic :: fi[u]; i; i = Dinic :: e[i].ne) {
		int v = Dinic :: e[i].to - n, w = Dinic :: e[i].ew;
		if(1 <= v && v <= n && ! w) {
			print(a[u], a[v]);
			dfs(v);
		} 
	}
}
void solve() {
	cin >> d >> n;
	FOR(i, 1, n) {
		string s; cin >> s;
		ROF(j, d - 1, 0) a[i] = a[i] << 1 | (s[j] == '1');
	}
	n ++;
	sort(a + 1, a + n + 1);
	int S = 0, T = n * 2 + 1;
	Dinic :: init();
	FOR(i, 2, n) add(1, i + n, 1);
	FOR(i, 2, n) FOR(j, i + 1, n) if((a[i] & a[j]) == a[i])
		add(i, j + n, popcount(a[i]) + 1);
	FOR(i, 1, n) Dinic :: add(S, i, 1);
	FOR(i, 1, n) Dinic :: add(i + n, T, 1);
	int ans = - 1;
	FOR(i, 1, n) ans += popcount(a[i]) + 1;
	ROF(i, d + 1, 1) {
		for(auto h : e[i])
			Dinic :: add(FI(h), SE(h), 1);
		ans -= Dinic :: dinic(S, T) * i;
	}
	cout << ans << endl;
	FOR(i, 1, n) if(! vis[i]) {
		if(i > 1) cout << "R ";
		print(0, a[i]);
		dfs(i);
	}
}

CF1336E1 - Chiori and Doll Picking (easy version)

首先将所有 \(n\) 个数插入线性基，有经典结论，线性基 \(A\) 里能异或出来的数的方案数都是 \(2^{n-|A|}\)，因为无论外边 \(n-|A|\) 个数怎么异或，线性基里总能得出一种异或方法异或到某个数。

接下来就只需在线性基里计算即可，但是线性基大小比较大，比较难计算。

考虑拆成高低位，不难发现低位是影响不到高位的，所以将高位异或出的数的高位部分独立出来，设 \(g_S\) 为低位中异或出来为 \(S\) 的方案数，设 \(f_{i,S}\) 为高位中异或出来的数，在高位的 popcount 为 \(i\)，低位部分为 \(S\) 的方案数。

接下来对于每个高位 popcount 取值，都做使用 FWT 进行一遍异或卷积来计算低位异或部分：

\[h_{i,S}=\sum_{j\oplus k=S}f_{i,j}g_k \]

就能得出不同低位取值和高位 popcount 的方案数，然后就能直接统计出答案了。

时间复杂度　\(O(m^22^\frac{m}{2}+nm)\)。

ケロシの代码 
const int N = 40;
const int P = 998244353;
const int P2 = (P + 1) / 2;
inline int add(int x, int y) { return (x + y < P ? x + y : x + y - P); }
inline void Add(int & x, int y) { x = (x + y < P ? x + y : x + y - P); }
inline int sub(int x, int y) { return (x < y ? x - y + P : x - y); }
inline void Sub(int & x, int y) { x = (x < y ? x - y + P : x - y); }
inline int mul(int x, int y) { return (1ll * x * y) % P; }
inline void Mul(int & x, int y) { x = (1ll * x * y) % P; }
int fp(int x, int y) {
	int res = 1;
	for(; y; y >>= 1) {
		if(y & 1) Mul(res, x);
		Mul(x, x);
	}
	return res;
}
int n, m;
ll b[N];
int p[N], len, a[20][1 << 18];
int f[1 << 18], g[1 << 18];
int ans[N];
void insert(ll x) {
	ROF(i, m - 1, 0) if(x >> i & 1) {
		if(! b[i]) {
			b[i] = x;
			return;
		}
		x ^= b[i];
	}
}
void XOR(int * a, int lim) {
	for(int i = 1; i < lim; i <<= 1) 
		for(int j = 0; j < lim; j += (i << 1))
			REP(k, i) {
				int x = a[j + k];
				int y = a[j + k + i];
				a[j + k] = add(x, y);
				a[j + k + i] = sub(x, y);
			}
}
void IXOR(int * a, int lim) {
	for(int i = 1; i < lim; i <<= 1) 
		for(int j = 0; j < lim; j += (i << 1))
			REP(k, i) {
				int x = mul(a[j + k], P2);
				int y = mul(a[j + k + i], P2);
				a[j + k] = add(x, y);
				a[j + k + i] = sub(x, y);
			}
}
void solve() {
	cin >> n >> m;
	REP(_, n) {
		ll x; cin >> x;
		insert(x);
	}
	int mid = m / 2;
	FOR(i, mid, m - 1) if(b[i]) p[len ++] = i;
	REP(S, 1 << len) {
		ll val = 0;
		REP(i, len) if(S >> i & 1) val ^= b[p[i]];
		a[popcount(val >> mid)][val & ((1 << mid) - 1)] ++;
	}
	len = 0;
	REP(i, mid) if(b[i]) p[len ++] = i;
	REP(S, 1 << len) {
		ll val = 0;
		REP(i, len) if(S >> i & 1) val ^= b[p[i]];
		g[val] ++;
	}
	XOR(g, 1 << mid);
	FOR(i, 0, m - mid) {
		REP(S, 1 << mid) f[S] = a[i][S];
		XOR(f, 1 << mid);
		REP(S, 1 << mid) Mul(f[S], g[S]);
		IXOR(f, 1 << mid);
		REP(S, 1 << mid) Add(ans[i + popcount(S)], f[S]);
	}
	int sz = 0;
	REP(i, m) if(b[i]) sz ++;
	FOR(i, 0, m) Mul(ans[i], fp(2, n - sz));
	FOR(i, 0, m) cout << ans[i] << " "; cout << endl;
}

CF1336E2 - Chiori and Doll Picking (hard version)

首先设 \(n\) 个数插入线性基为 \(A\)，其秩 \(|A|\) 为 \(k\)。

考虑当 \(k\) 很小的时候可以暴力枚举 \(A\) 里所有 \(2^k\) 个数，时间复杂度 \(O(2^k)\)。

考虑 \(k\) 较大时怎么做，考虑设线性基 \(B\)，使得 \(B\) 是 \(A\) 的一个正交基，满足：

\[y \in B \Leftrightarrow \forall x\in A , \langle x,y \rangle =0 \]

其中运算 \(\langle x,y \rangle =|x ~\mathrm{and}~ y| \bmod 2\)。

定义集合 $F_c=\left \{ x \mid |x|=c, x \subseteq U \right \} $。

接下来尝试用 \(B\) 来表示 \(A\)：

\[[x \in A]=\frac{1}{|B|}\sum_y (-1)^{ \langle x,y \rangle } [y \in B] \]

然后就能表示答案：

\[\begin{aligned} \sum_{x\in F_c}[x \in A] & = \sum_{x\in F_c} \frac{1}{|B|} \sum_y (-1)^{ \langle x,y \rangle } [y \in B]\\ & = \frac{1}{|B|} \sum_y [y \in B] \sum_{x\in F_c} (-1)^{ \langle x,y \rangle } \end{aligned} \]

考虑计算系数 \(\sum_{x\in F_c} (-1)^{ \langle x,y \rangle }\)：

\[\sum_{x\in F_c} (-1)^{ \langle x,y \rangle }= \sum_{|x ~\mathrm{and} ~y|=k}(-1)^k \binom{|y|}{k} \binom{m-|y|}{|x|-k} \]

不难发现这个只和 \(|y|\) 有关，所以可以用 \(O(m^3)\) 算出所有系数 \(w_{c,d}=\sum_{x\in F_c,|y|=d} (-1)^{ \langle x,y \rangle }\)。

接下来要构造出 \(A\) 的正交 \(B\)。

考虑一种构造方式：先把 \(A\) 进行高斯消元，令 \(A\) 与 \(B\) 的主元是互补的，然后把 \(A\) 的非主元部分反转到 \(B\) 的主元部分。

展示一下官方图：

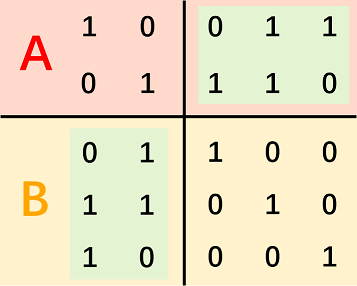
这里大致理解一下，假设一个 \(x \in A\) 和 \(y \in B\)，然后 \(x\) 和 \(y\) 有一位都是 \(1\)，那么通过上面的翻转，应该有对应的一位也都是 \(1\)，所以 \(|x ~\mathrm{and}~ y|\) 都是偶数。

因为 \(A\) 与 \(B\) 主元互补，所以 \(B\) 的秩为 \(m-k\)，所以可以把 \(B\) 中的 \(2^{m-k}\) 个数全部枚举一遍，然后直接乘上系数统计一下即可，时间复杂度 \(O(2^{m-k})\)。

在两种方法里选择更优的一种即可平衡复杂度。

时间复杂度 \(O(2^\frac{m}{2}+m^3+nm)\)。

ケロシの代码 
const int N = 60;
const int P = 998244353;
inline int add(int x, int y) { return (x + y < P ? x + y : x + y - P); }
inline void Add(int & x, int y) { x = (x + y < P ? x + y : x + y - P); }
inline int sub(int x, int y) { return (x < y ? x - y + P : x - y); }
inline void Sub(int & x, int y) { x = (x < y ? x - y + P : x - y); }
inline int mul(int x, int y) { return (1ll * x * y) % P; }
inline void Mul(int & x, int y) { x = (1ll * x * y) % P; }
inline int sgn(int x) { return (x & 1) ? P - 1 : 1; }
int fp(int x, int y) {
	int res = 1;
	for(; y; y >>= 1) {
		if(y & 1) Mul(res, x);
		Mul(x, x);
	}
	return res;
}
int n, m;
int C[N][N];
ll b[N], a[N], d[N], len;
int f[N], w[N][N], ans[N];
void insert(ll x) {
	ROF(i, m - 1, 0) if(x >> i & 1) {
		if(! b[i]) {
			b[i] = x;
			return;
		}
		x ^= b[i];
	}
}
void dfs(int u, ll x) {
	if(u == len + 1) {
		f[__builtin_popcountll(x)] ++;
		return;
	}
	dfs(u + 1, x);
	dfs(u + 1, x ^ d[u]);
}
void solve() {
	cin >> n >> m;
	FOR(i, 0, m) {
		C[i][0] = 1;
		FOR(j, 1, m) C[i][j] = add(C[i - 1][j - 1], C[i - 1][j]);
	}
	REP(_, n) {
		ll x; cin >> x;
		insert(x);
	}
	ROF(i, m - 1, 0) FOR(j, i + 1, m - 1) if(b[j] >> i & 1) b[j] ^= b[i];
	int mid = (m + 1) / 2, sz = 0;
	REP(i, m) if(b[i]) sz ++;
	if(sz <= mid) {
		REP(i, m) if(b[i]) d[++ len] = b[i];
		dfs(1, 0);
		FOR(i, 0, m) cout << mul(f[i], fp(2, n - sz)) << " ";
		cout << endl;
	}
	else {
		REP(i, m) REP(j, m) if(b[i] >> j & 1) a[j] |= 1ll << i;
		REP(i, m) a[i] ^= 1ll << i;
		REP(i, m) if(a[i]) d[++ len] = a[i];
		dfs(1, 0);
		FOR(i, 0, m) FOR(j, 0, m) FOR(k, 0, i)
			Add(w[i][j], mul(sgn(k), mul(C[j][k], C[m - j][i - k])));
		FOR(i, 0, m) FOR(j, 0, m) Add(ans[i], mul(f[j], w[i][j]));
		FOR(i, 0, m) Mul(ans[i], fp(2, n - sz));
		FOR(i, 0, m) Mul(ans[i], fp((P + 1) / 2, m - sz));
		FOR(i, 0, m) cout << ans[i] << " ";
		cout << endl;
	}
}

UOJ R28B - 环环相扣

不妨设 \(a_i>a_j>a_k\)，那么最优的排法只有两种情况：

  1. \((a_i \bmod a_j) + (a_j \bmod a_k) + a_k\)
  2. \((a_i \bmod a_k) + a_j + a_k\)。

引理：若正整数 \(x>y\) 则 \((x \bmod y)+ y\le x\)。

证明不难：\((x \bmod y)+y \le (x - y)+y = x\)。

接下来通过手玩，寻找性质。

结论 1：区间的最大值和次大值是必选的。

证明，考虑将区间中的数从大到小排序，最大的是 \(a_1\)，次大是 \(a_2\)，以此类推。

考虑一个下界是选 \(a_1,a_2,a_3\)，用第二种排法，得到下界为 \((a_1 \bmod a_3)+a_2+a_3 \ge a_2+a_3\)。

考虑排法一：推公式来找到上界：

\[\begin{aligned} &(a_i \bmod a_j)+(a_j \bmod a_k)+a_k \\ \le & (a_i \bmod a_j)+a_j \\ \le & \min( a_i,(a_j-1)+a_j) \\ \le & \min( a_i,2a_j-1) \end{aligned} \]

很明显不选最大和次大是不优的。

考虑排法二：

\[(a_i \bmod a_k)+a_j+a_k \le a_i+a_j \]

如果不取 \(a_1\) 就无法超过上界，如果取 \(a_1\)，因为式子中 \(a_j\) 是独立的，所以取到 \(a_2\) 是最优的，必须要选最大和次大。

所以区间最大和次大必选。

区间枚举 \(a_k\) 的位置即可做到 \(O(nq)\)。

接下来设 \(F(l,r,i)\) 为区间 \([l,r]\) 排除了 \(i\) 和排除了 \([l,i-1]\cup [i+1,r]\) 中的最大值，中最大的 \((a_i \bmod a_k + a_k)\)。

那么设查询区间最大值为 \(a_i\)，次大值为 \(a_j\) 两种排法的价值可以重写：

  1. \(F(l,r,j)+(a_i \bmod a_j)\)
  2. \(F(l,r,i)+a_j\)

这个比较难算，考虑把 \(F(l,r,i)\) 拆成两部分：\(F(l,i,i)\) 和 \(F(i,r,i)\)。

这样可以预处理，从 \(i\) 开始往左或者往右扫。

注意拆分后可能会把 \(a_k\) 排掉，需要再算一遍这个。

这样时间复杂度降为了 \(O(n^2+q \log n)\)。

结论 2：预处理 \(F(l,i,i)\) 或 \(F(i,r,i)\) 的过程中，若扫到两个 \(a_k>\frac{1}{2}a_i\)，则可以停止扫描。

需要扫两个是因为有一个可能会被当作最大值排掉。

因为 \(\frac{1}{2}a_i<a_k<a_i\)，所以 \((a_i \bmod a_k + a_k)=(a_i-a_k)+a_k=a_i\)，已经顶到上界，不用再扫了。

这样总扫描次数就是 \(O(n \log V)\) 的了。

时间复杂度 \(O(n \log V + q \log n)\)。

ケロシの代码 
namespace IO {
	char buf[1024], * p1 = buf, * p2 = buf;
	inline char gc() {
		if(p1 == p2) {
			p2 = buf + fread(buf, 1, sizeof buf, stdin);
			p1 = buf;
		}
		return p1 == p2 ? EOF : * p1 ++;
	}
	ll read() {
		ll res = 0; int v = 0;
		char c = gc();
		while(c < '0' || c > '9') {
			if(c == '-') v = 1;
			c = gc();
		}
		while('0' <= c && c <= '9') {
			res = (res << 3) + (res << 1) + (c ^ 48);
			c = gc();
		}
		return v ? - res : res;
	}
}
using IO :: read;
const int N = 2e6 + 5;
const ll LNF = 1e18;
int n, m, op;
ll a[N];
vector<pair<int, ll>> f[N], g[N];
struct SgT {
	int le[N << 2], ri[N << 2];
	int D[N << 2];
	void pushup(int u) {
		D[u] = a[D[u << 1]] >= a[D[u << 1 | 1]] ? D[u << 1] : D[u << 1 | 1];
	}
	void build(int u, int l, int r) {
		le[u] = l, ri[u] = r;
		if(l == r) {
			D[u] = l;
			return;
		}
		int mid = l + r >> 1;
		build(u << 1, l, mid);
		build(u << 1 | 1, mid + 1, r);
		pushup(u);
	}
	int query(int u, int l, int r) {
		if(l > r) return 0;
		if(l <= le[u] && ri[u] <= r) {
			return D[u];
		}
		int mid = le[u] + ri[u] >> 1;
		if(r <= mid) return query(u << 1, l, r);
		if(mid < l) return query(u << 1 | 1, l, r);
		int L = query(u << 1, l, r);
		int R = query(u << 1 | 1, l, r);
		return a[L] >= a[R] ? L : R;
	}
} t;
ll F(int l, int r, int i) {
	ll res = - LNF;
	int L = 0, R = SZ(g[i]) - 1;
	while(L <= R) {
		int mid = L + R >> 1;
		if(FI(g[i][mid]) <= r) {
			chmax(res, SE(g[i][mid]));
			L = mid + 1;
		}
		else {
			R = mid - 1;
		}
	}
	L = 0, R = SZ(f[i]) - 1;
	while(L <= R) {
		int mid = L + R >> 1;
		if(FI(f[i][mid]) >= l) {
			chmax(res, SE(f[i][mid]));
			L = mid + 1;
		}
		else {
			R = mid - 1;
		}
	}
	return res;
}
void solve() {
	n = read(); m = read(); op = read();
	FOR(i, 1, n) a[i] = read();
	FOR(l, 1, n) {
		ll res = - LNF; int pos = 0, cnt = 0;
		FOR(i, l + 1, n) {
			ll x = 0;
			if(a[i] > a[pos]) x = a[pos], pos = i;
			else x = a[i];
			if(x && chmax(res, a[l] % x + x))
				g[l].push_back({i, res});
			if(a[i] > a[l] / 2) cnt ++;
			if(cnt == 2) break;
		}
		res = - LNF; pos = cnt = 0;
		ROF(i, l - 1, 1) {
			ll x = 0;
			if(a[i] > a[pos]) x = a[pos], pos = i;
			else x = a[i];
			if(x && chmax(res, a[l] % x + x))
				f[l].push_back({i, res});
			if(a[i] > a[l] / 2) cnt ++;
			if(cnt == 2) break;
		}
	}
	t.build(1, 1, n);
	ll lst = 0;
	REP(_, m) {
		int l, r;
		l = read(); r = read();
		if(op) {
			l = (lst + l) % n; if(! l) l = n;
			r = (lst + r) % n; if(! r) r = n;
		}
		int p1 = t.query(1, l, r);
		int pl = t.query(1, l, p1 - 1);
		int pr = t.query(1, p1 + 1, r);
		int p2 = a[pl] > a[pr] ? pl : pr;
		ll res = - LNF;
		chmax(res, F(l, r, p1) + a[p2]);
		chmax(res, F(l, r, p2) + a[p1] % a[p2]);
		if(p1 < p2) {
			if(l < p1) {
				int p3 = t.query(1, l, p1 - 1);
				chmax(res, a[p1] % a[p3] + a[p3] + a[p2]);
			}
			if(p2 < r) {
				int p3 = t.query(1, p2 + 1, r);
				chmax(res, a[p2] % a[p3] + a[p3] + a[p1] % a[p2]);
			}
		}
		if(p2 < p1) {
			if(p1 < r) {
				int p3 = t.query(1, p1 + 1, r);
				chmax(res, a[p1] % a[p3] + a[p3] + a[p2]);
			}
			if(l < p2) {
				int p3 = t.query(1, l, p2 - 1);
				chmax(res, a[p2] % a[p3] + a[p3] + a[p1] % a[p2]);
			}
		}
		cout << (lst = res) << endl;
	}
}

AT NOMURA2020F - Sorting Game

先考虑固定的 \(a\) 数组，对于 \(i<j\) 且 \(a_i>a_j\) 的对，\(i\) 和 \(j\) 必须相邻交换一次，所以对于所有的 \(i<j\) 且 \(a_i>a_j\)，必须满足 \(a_i\) 与 \(a_j\) 数位上只差一位。

更深入的，这就相当于 \(a_i\) 和 \(a_j\) 的第一个不同高位，\(a_i\) 的是 \(1\) 且 \(a_j\) 是 \(0\)，且下面的位全部相同。

再考虑如果要修改这个 \(a\) 数组，一次修改只会推平一个位，两个数的不同位数并不会增大，只会操作最高不同位，使得 \(a_i<a_j\) 变为 \(a_i>a_j\)。

不难发现上述的交换和改数组都是高位到低位，所以考虑 dp。

社 \(f_{n,m}\) 为数组长为 \(m\)，值域为 \([0,2^n)\) 的答案，那么考虑最高位是什么情况。

第一种是不存在 \(10\) 逆序对，形如 \(00\cdots 0011\cdots 11\)，这时因为有左边 \(0\) 部分小于右边 \(1\) 部分，所以最佳改数组方案就是推平这一位，这样这一位的偏序就没有用了，相当于去掉这一位，递归进子问题。\(01\) 分割点有 \(m+1\) 种选法，方案即为 \((m+1)f_{n-1,m}\)。

第二种是存在 \(10\) 逆序对，考虑提出最左的 \(1\) 和最右的 \(0\)，形如 \(0001\cdots 0111\)，那么根据上述的性质，中间的 \(1\cdots 0\) 段下面的位都是相同的，直接随最左的 \(1\) 固定掉。接下来仍然可以推平这一位，使得最左的 \(0\) 段和最右的 \(1\) 段失去偏序关系，所以继续递归进子问题，枚举保留的有 \(i\) 位，那么方案为 \(\sum_{i=1}^{m-1}i \cdot 2^{m-i+1}f_{n-1,i}\)。

用前缀和优化这个转移即可，时间复杂度 \(O(n^2)\)。

ケロシの代码 
const int N = 5e3 + 5;
const int P = 1e9 + 7;
inline int add(int x, int y) { return (x + y < P ? x + y : x + y - P); }
inline void Add(int & x, int y) { x = (x + y < P ? x + y : x + y - P); }
inline int mul(int x, int y) { return (1ll * x * y) % P; }
inline void Mul(int & x, int y) { x = (1ll * x * y) % P; }
int n, m;
int f[N][N], g[N][N];
void solve() {
	cin >> n >> m;
	FOR(j, 1, m) f[0][j] = 1;
	FOR(j, 1, m) g[0][j] = add(mul(g[0][j - 1], 2), mul(j, f[0][j]));
	FOR(i, 1, n) FOR(j, 1, m) {
		f[i][j] = mul(f[i - 1][j], j + 1);
		Add(f[i][j], g[i - 1][j - 1]);
		g[i][j] = add(mul(g[i][j - 1], 2), mul(j, f[i][j]));
	}
	cout << f[n][m] << endl;
}

AT JOISC2017E - 壊れた機器 (Broken Device)

考虑坏掉的位是零，所以需要用含有 \(1\) 的信息来表达进制中的 \(0\)。

这样的话一个位就表达不了信息，考虑用两个位存一个进制。

两个位可以存三种状态：\(01,10,11\)，发现这可以表示三进制，分别对应 \(0,1,2\)。

但是最坏情况下这样不坏掉的两个位最少只有 \(\frac{150-40\times 2}{2}=35\) 个，只能表达 \(3^{35}\) 级别的数，而 \(10^{18}\) 需要 \(38\) 个位来表示。

考虑将位随机乱排，这样坏掉的位有几率排到一起，有效位就能增加，但不足以通过。

考虑有两个位，前一个位坏了但后一个是好的，那么这个两个位依然可以表示 \(01\)，将这类情况下的位也充分利用，即可通过 \(N=150\)。

ケロシの代码 
#include "Broken_device_lib.h"
const int N = 205;
int t[N], b[N], id[N];
void Anna(int n, ll x, int k, int * p) {
	mt19937 rnd(114);
	REP(i, n) id[i] = i;
	shuffle(id, id + n, rnd);
	REP(i, n) t[i] = b[i] = 0;
	REP(i, k) t[p[i]] = 1;
	int pos = 0;
	while(x) {
		int val = x % 3;
		if(val == 0) {
			while(t[id[pos]]) pos += 2;
			b[id[pos]] = 1;
		}
		if(val == 1) {
			while(t[id[pos + 1]]) pos += 2;
			b[id[pos + 1]] = 1;
		}
		if(val == 2) {
			while(t[id[pos]] || t[id[pos + 1]]) pos += 2;
			b[id[pos]] = b[id[pos + 1]] = 1;
		}
		pos += 2;
		x /= 3;
	}
	REP(i, n) Set(i, b[i]);
}
ll Bruno(int n, int * a) {
	mt19937 rnd(114);
	REP(i, n) id[i] = i;
	shuffle(id, id + n, rnd);
	ll x = 0;
	for(int pos = n - 2; pos >= 0; pos -= 2) {
		if(! a[id[pos]] && ! a[id[pos + 1]]) continue;
		x *= 3;
		if(a[id[pos]] && a[id[pos + 1]]) x += 2;
		if(! a[id[pos]] && a[id[pos + 1]]) x += 1;
	}
	return x;
}

考虑足以通过 \(N=120\) 甚至更小的更优做法。

考虑随机 \(n\) 个数 \(a_i\)，如果构造出来的序列中第 \(i\) 位是 \(1\) 就表示答案就异或上 \(a_i\)。

这样只需选定一些数异或出目标数，使用线性基维护即可。

ケロシの代码 
#include "Broken_device_lib.h"
const int N = 1000;
ll a[N], b[N], w[N];
int t[N], id[N], ans[N]; 
void insert(ll x, int u) {
	ll res = 0;
	ROF(i, 60, 0) if(x >> i & 1) {
		if(! b[i]) {
			b[i] = x;
			id[i] = u;
			w[i] = res ^ (1ll << i);
			return;
		}
		x ^= b[i];
		res ^= w[i];
	}
}
void Anna(int n, ll x, int k, int * p) {
	mt19937 rnd(114);
	REP(i, n) a[i] = 1ull * rnd() * rnd() % (1ll << 60);
	REP(i, 61) w[i] = b[i] = 0;
	REP(i, n) ans[i] = t[i] = 0;
	REP(i, k) t[p[i]] = 1;
	REP(i, n) if(! t[i]) insert(a[i], i);
	ll res = 0;
	ROF(i, 60, 0) if(x >> i & 1) {
		x ^= b[i];
		res ^= w[i];
	}
	ROF(i, 60, 0) if(res >> i & 1) ans[id[i]] = 1; 
	REP(i, n) Set(i, ans[i]);
}
ll Bruno(int n, int * p) {
	mt19937 rnd(114);
	REP(i, n) a[i] = 1ull * rnd() * rnd() % (1ll << 60);
	ll res = 0;
	REP(i, n) if(p[i]) res ^= a[i];
	return res;
}

SYSUCPC 2024 Final M - Make SYSU Great Again 3

首先考虑是链怎么做到答案为 \(\left \lceil \frac{n}{2} \right \rceil -1\)，考虑将排列分为奇数位和偶数位，对于偶数位，都填 \(\left [1,\left \lfloor \frac{n}{2} \right \rfloor \right ]\) 中的数，奇数位填其余的数。

接下来就不难想到一个构造，偶数位直接从 \(1\) 开始填，不断填到大的，然后偶数位在满足条件时类似折返一样填即可，例如：

\[\color{red} 7 ~ \color{blue} 1 ~ \color{red} 8 ~ \color{blue} 2 ~ \color{red} 6 ~ \color{blue} 3 ~ \color{red} 9 ~ \color{blue} 4 ~ \color{red} 5 \]

\[\color{red} 8 ~ \color{blue} 1 ~ \color{red} 9 ~ \color{blue} 2 ~ \color{red} 7 ~ \color{blue} 3 ~ \color{red} {10} ~ \color{blue} 4 ~ \color{red} 6 ~ \color{blue} 5 \]

然后考虑是环怎么做，不难发现可以交换前两项，这样不影响最左边三个数的匹配，同时开头的 \(1\) 给最后两个数也产生了贡献：

\[\color{blue} 1 ~ \color{red} 7 ~ \color{red} 8 ~ \color{blue} 2 ~ \color{red} 6 ~ \color{blue} 3 ~ \color{red} 9 ~ \color{blue} 4 ~ \color{red} 5 \]

\[\color{blue} 1 ~ \color{red} 8 ~ \color{red} 9 ~ \color{blue} 2 ~ \color{red} 7 ~ \color{blue} 3 ~ \color{red} {10} ~ \color{blue} 4 ~ \color{red} 6 ~ \color{blue} 5 \]

ケロシの代码 
const int N = 2e5 + 5;
int n, a[N];
void solve() {
	cin >> n;
	FOR(i, 1, n) a[i] = 0;
	if(n % 2) {
		for(int i = 1, p = 2; p <= n; p += 2, i ++)
			a[p] = i;
		for(int i = n / 2 + 1, p = n; p >= 1; p -= 4, i ++)
			a[p] = i;
		for(int i = n, p = n - 2; p >= 1; p -= 4, i --)
			a[p] = i;
		swap(a[1], a[2]);
	}
	else {
		for(int i = 1, p = 2; p <= n; p += 2, i ++)
			a[p] = i;
		for(int i = n / 2 + 1, p = n - 1; p >= 1; p -= 4, i ++)
			a[p] = i;
		for(int i = n, p = n - 3; p >= 1; p -= 4, i --)
			a[p] = i;
		swap(a[1], a[2]);
	}
	cout << "Yes" << endl;
	FOR(i, 1, n) cout << a[i] << " "; cout << endl;
}
posted @ 2025-01-02 21:15  KevinLikesCoding  阅读(40)  评论(0)    收藏  举报