支持向量机(support vector machine)

画布多说 ？？？ 什么画布，啊呸，话不多说，无图无真相，先上图：

                                                           

支持向量机，让大家都支持一下！之前看一个写博文很好的博主说，支持向量机算法算是属于实际比较主流的分类算法了，为啥加实际两个字呢？因为权衡工业界和学术界，很多算法牛逼却不能实际应用起来，但是SVM确实是奇迹，两边都吃的开，就是这么稳，也难怪这小哥要鱼目混珠了哈哈

进入正题，之前在感知机(perceptron)中我们了解到,当训练数据集线性可分时，感知机学习算法存在无穷多个解，其解由于不同的初始值或者不同的迭代顺序而有所不同，究其原因，还是因为感知机是一种误分类驱动的算法。

那我们支持向量机呢？答案是唯一的，钢铁直男，独一无二，因为支持向量机在线性可分数据集下的优化遵循的是间隔最大化，可以这么理解，单纯看硬间隔下的线性支持向量机，其就是在感知机所有可能的分类平面中寻找一条最优秀的，得天独秀。

下面来正式介绍一下线性支持向量机的定义：

给定线性可分的训练数据集，通过间隔最大化或者等价的求解相应的凸二次规划问题学习得到的分离超平面为：

\omega ^{*}\cdot x+b^{*}=0

以及相应的分类决策函数：f(x)=sign(w^{*}\cdot x+b^{*})

不看先决条件，是不是觉得和感知机的公式一毛一样啊，哈哈，别忘了我们的间隔最大化！

 

(图片来自于百度)

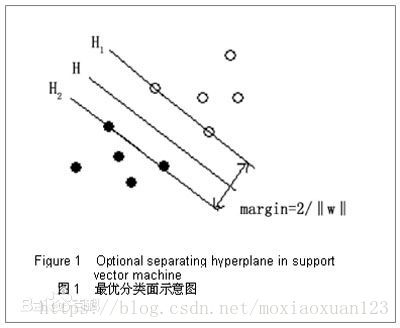
如上图所示，白色是正实例点，黑色是负实例点，此时，将黑白点正确分类的线段或者超平面有很多，但是SVM对应着将两类数据正确划分且间隔最大的那条直线。

 

为了方便后续的说明，这里插播两个概念，函数间隔和几何间隔：已经晓得什么是函数间隔和几何间隔的童鞋可以跳过这部分

这里涉及到一个很直观的想法，就是点离分离超平面的距离越远，那么它被认为是当前所属类别的可信度就越高，而点离分离超平面越近，那么稍不留神或者轻微的扰动就可以让你分类错误，所以，支持向量机为了用科学的方法来衡量这个直观的感受，定义了函数间隔和几何间隔。

函数间隔和几何间隔：

对于给定的训练数据集T和超平面(w,b)，定义超平面(w,b)关于样本点(x_{i},y_{i})的函数间隔为：

\hat{\gamma _{i}}= y_{i}(w\cdot x_{i}+b)

定义超平面关于训练数据集T的函数间隔为，数据集中所有样本点到分类超平面的函数间隔的最小值，公式如下：

\hat{\gamma }=\min _{i=1...,N}\hat{\gamma _{i}}

通过定义函数间隔可以表示分类预测的正确性及确信度，但是这个地方还存在一个问题，就是当w和b成倍的增加的时候，导致的函数间隔也会成倍的增加，为了解决这个问题，增加了一条新的限制，给超平面的法向量增加一些约束，比如说||w||=1，使得间隔是确定的，这个间隔就是所谓的几何间隔了。

集合间隔的公式定义如下：

\gamma _{i}=\frac{w}{||w||}\cdot x_{i}+\frac{b}{||w||} 同样的，我们取训练样本数据集中的最小值，作为整个样本关于分类超平面的几何间隔。

 

间隔最大化

这里的间隔最大化的间隔指的是硬间隔，对应于后面文章讲到的软间隔。

间隔最大化的直观解释就是，我们不仅可以将数据点全部正确的分类，我们还要求所有分类点离分类平面尽可能的远，这种偏执的思想有点像苹果公司的作风，这样选出来的分类超平面应该会对未知的数据点也有较好的分类能力！

从数学的角度上如何选出这个间隔最大的分离超平面呢？

前面说过，间隔最大化可以转化为约束优化问题，如下：

\max _{w,b} \gamma

s.t. y_{i}\left ( \frac{w}{||w||}\cdot x_{i}+\frac{b}{||w||} \right )\geq \gamma

看公式不难理解，我们要求每一个点到超平面的距离都不得小于grammar，同时尽量的使这个grammar最大，就是我们间隔最大化完成的目的

这里我们将几何间隔变成函数间隔：

\max _{w,b} \frac{\hat{\gamma}}{||w||}

s.t. y_{i}\left ( w \cdot x_{i}+b \right )\geq \hat{\gamma}，i=1,2,3....N

并且我们发现，函数间隔的改变对我们求解上述优化问题并没有什么影响，因为，你求出来的函数间隔不论乘以多少倍，你得到的(w,b)也会跟着相乘多少倍，但是在表示平面的方程里，同时放大缩小多少倍其实还是代表着相同的那个平面，所以，我们取特例将函数间隔设为1,而且发现最大化\frac{1}{||w||}实际上和最小化\frac{1}{2}||w||^{2}是等价的（将最大化转换为最小化问题是最优化理论的一个直观想法）,于是我们整个的优化过程就变成：

\min \frac{1}{2}||w||^{2}

s.t. y_{i}\left ( w \cdot x_{i}+b \right )-1\geq 0

这是一个凸二次规划问题，接下来我们就需要对这个优化问题动手动脚了，呸，动动手脚！

当我们求得了对应的最优解w^{*},b^{*}问题就算解决了。

接下来介绍的是学习的对偶算法

对偶算法，是不是听名字就令人作呕啊哈哈哈哈，在前面的感知机里也提到过对偶问题，支持向量机下对偶问题的研究是十分有必要的，一方面可以引出核技巧，对核方法有着更直观的理解，另一方面可以对什么是支持向量有着更感性的认识。

前面说道，间隔最大化最终会转化成为

\min \frac{1}{2}||w||^{2}

s.t. y_{i}\left ( w \cdot x_{i}+b \right )-1\geq 0

这样一个凸二次规划问题，那么根据拉格朗日对偶性，可以通过求解对偶问题得到原始问题的最优解，首先构造拉格朗日函数：

L(w,b,a)=\frac{1}{2}||w||^{2}-\sum_{i=1}^{N}\alpha _{i}y_{i}(w\cdot x_{i}+b)+\sum_{i=1}^{N}\alpha _{i}

如果对拉格朗日对偶性不理解的可以查阅相关资料或者等我后续的更新

根据拉格朗日对偶性，原始问题可以转化对偶的极大极小问题,emmmm......原始问题是极小极大问题，至于为什么，请等我更新

\max _{\alpha } \min_{w,b}L(w,b,\alpha )

那么很直观的思路我们需要先求内部的极小问题，得到关于alpha的函数，然后再求外面的关于alpha的最大化

 

那么首先L(w,b,a)分别对w,b求偏导数，可以得：

w-\sum_{i=1}^{N}\alpha _{i}y_{i}x_{i}=0

-\sum_{i=1}^{N}\alpha _{i}y_{i}=0

将求导得到的结果代入到拉格朗日函数中，并进行整理，得到如下结果：

L(w,b,\alpha )=\tfrac{1}{2}\sum_{i=1}^{N}\alpha _{i}\alpha _{j}y_{i}y_{j}(x_{i}\cdot x_{j})-\sum_{i=1}^{N}\alpha _{i}y_{i}\left ( \left ( \sum_{j=1}^{N}\alpha _{j}y_{j}x_{j} \right )\cdot x_{i}+b \right )+\sum_{i=1}^{N}\alpha _{i}

L(w,b,\alpha )=-\tfrac{1}{2}\sum_{i=1}^{N}\alpha _{i}\alpha _{j}y_{i}y_{j}(x_{i}\cdot x_{j})+\sum_{i=1}^{N}\alpha _{i}

内层求最小值结束之后，就进行求外层的最大值即对\alpha的极大值。

\max_{\alpha } -\tfrac{1}{2}\sum_{i=1}^{N}\alpha _{i}\alpha _{j}y_{i}y_{j}(x_{i}\cdot x_{j})+\sum_{i=1}^{N}\alpha _{i}

s.t. \sum_{i=1}^{N}\alpha _{i}y_{i}=0

同样的，我们将求极大值问题转化为求极小值问题：

 

\min _{\alpha } \tfrac{1}{2}\sum_{i=1}^{N}\alpha _{i}\alpha _{j}y_{i}y_{j}(x_{i}\cdot x_{j})-\sum_{i=1}^{N}\alpha _{i}

s.t.      \sum_{i=1}^{N}\alpha _{i}y_{i}=0 且\alpha _{i}\geq 0

 

根据这个约束优化问题我们可以求得一组\alpha，并且可以利用\alpha将原问题的w,b顺利的求解出来，具体参照《统计学习方法》定理7.2

 

这里加上两点想法，关于核技巧和支持向量的看法：

 

1 核技巧体现在哪里？支持向量机哪里可以用到核技巧？

答：前面我们已经求出了w=\sum_{i=1}^{N}\alpha _{i}y_{i}x_{i}，那么将w代入到分离超平面的公式中可以得到，

\sum_{i=1}^{N}\alpha _{i}^{*}y_{i}(x\cdot x_{i})+b^{*}，进而得到分类决策函数：f(x)=sign\left ( \sum_{i=1}^{N}\alpha _{i}^{*}y_{i}(x\cdot x_{i})+b^{*}\right )

也就是说分类决策函数只依赖于输入x和训练样本输入的内积，此式子也成为线性可分支持向量机的对偶形式

有内积<xi,xj>就可以引入核技巧,并且可以将训练数据两两之间的内积提前算好放到一张表格中，加速计算，很有用！

更甚至，你都不需要求全部的训练数据的内积，只需要求支持向量的点之间的数据的内积就足够用了，为什么这么说呢？答案在第二问中。

2 你说的对偶形式可以对支持向量有着更好的理解？说好的理解呢？？？

答：我说对偶形式会对支持向量有更好的理解完全是骗你的，要不然你怎么会看这些复杂的推导呢，哈哈哈哈哈哈

不开玩笑了，也许我们可以从上述的一些推导中找出蛛丝马迹。

这里先给出结论就是 \alpha _{i}不为0的对应的xi的点都是支持向量，为什么这么说呢，看下式：

L(w,b,a)=\frac{1}{2}||w||^{2}-\sum_{i=1}^{N}\alpha _{i}{\color{Red} y_{i}(w\cdot x_{i}+b-1)}

这是我们之前得到的拉格朗日函数，只不过把ai提取出来合并到一起去了，那么所有是支持向量的点，红色部分其实是都是等于0的，因为我们支持向量的函数间隔为1,而那些不是支持向量的点求出的结果自然是大于1的，所以相减，必然大于0,不幸的是，我们这里求的是对于\alpha _{i}的极大化过程（参照前面的内部w,b极小化，外部\alpha _{i}极大化），而\alpha _{i}又必须是非负的，所以没办法啊，为了我们的极大化过程，只能将所有求出红色部分不等于0的点对应的\alpha _{i}全部设为0,这也就是为什么非0的\alpha _{i}对应的xi，yi一定是支持向量的道理，因为不是支持向量的统统被优化掉了。

 

还可以从另一方面理解，那就是KKT条件，KKT条件告诉我们，

\sum_{i=1}^{N}\alpha _{i}^{*}{{ y_{i}(w\cdot x_{i}+b-1)}}=0

而\alpha _{i}\geq 0和{{ y_{i}(w\cdot x_{i}+b-1)}}\geq 0是互补的KKT条件，那么当支持向量满足\alpha _{i}\geq 0时候，必然有{{ y_{i}(w\cdot x_{i}+b-1)}}= 0成立才能使得KKT条件继续成立，那么，仔细观察{{ y_{i}(w\cdot x_{i}+b-1)}}= 0此公式，我们发现，它就是支持向量点满足的方程，也就是说，只要\alpha _{i}\geq 0，那么它必然一定是支持向量！

 

写的比较仓促，有什么问题请留言，我会及时改正，感谢http://blog.pluskid.org/?p=682博主提供问题2第一个的宝贵思路！

 

posted @ 2018-08-06 18:42  西红柿炒蛋就加糖！  阅读(282)  评论(0)  编辑  收藏  举报