计算机图形学（三种画线算法）

第二章：光栅图形学算法

1、光栅显示器：光栅扫描式图形显示器简称光栅显示器，是画点设备，可看作是一个点阵单元发生器，并可控制每个点阵单元的亮度

2、由来：随着光栅显示器的出现，为了在计算机上处理、显示图形，需要发展一套与之相适应的算法。

3、研究内容：

1>直线段的扫描转换算法

2>多边形的扫描转换与区域填充算法

3>裁剪算法

4>反走样算法

5>消隐算法

一、直线段的扫描转换算法

1.为了显示一条直线，就在光栅显示器上用离散的像素点逼近直线，所以我们就要知道这些像素点的坐标

 

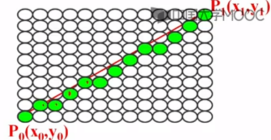
已知P0和P1，利用斜截式方程，y=kx+b,求出k=（y1-y0）/(x1-x0),b为截距

现在k,b已知，x,y未知，现在假设一个像素距离为y，即可求出y的值。

因为像素的坐标是整数，所以y值还要进行取整处理

2.在计算机中加法的运算更快，乘法较慢，故可以把上述方法优化来提高效率

1>数值微分法（DDA）

2>中点划线法

3>Bresenham算法

数值微分法（DDA）-----增量算法（只有一个加法）

 

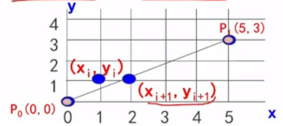
这个式子的含义是：当前步的y值等于前一步的y值加上斜率k（增量）

例子：

 

思考：x递增1，y递增k，是否适合任意的k？

可改进的点：

1>一般情况下，k都是小数，且每一步均要对y四舍五入，唯一改进的途径是把浮点运算变为整数加法！

2>方程还有两点式，一般式

当|k|<=1时，伪代码如下：

voidDDALine(int x0,int y0,int x1,int y1,int color){

Int x;

Float dx,dy,y,k;

dx=x1-x0;dy=y1-y0;

K=dy/dx;y=y0;

For(x=x0,x<=x1;x++){

Drawpixel(x,int(y+0.5),color);//drawpixel(x, y, color)在(x, y)像素点绘制颜色为color的点

Y=y+k;

}

}

中点画线法

 

采用直线的一般式方程：Ax+By+C=0  F(x,y)=0，其中a = y0 - y1， b = x1 - x0，c = x0y1 - x1y0

令F(x, y)=0则得出直线方程，代入 (x0, y0)和(x1, y1)，便可得到三个方程，可求出a,b,c的值

一条直线把平面分成了三个部分，直线上方，直线上，直线下方

 

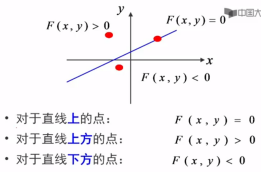
x方向上+1，y方向上加不加1需判断

 

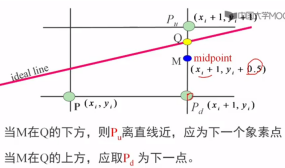
如何判断Q在M的上方还是下方？

把M点的坐标带入方程,其中a = y0 - y1， b = x1 - x0

 

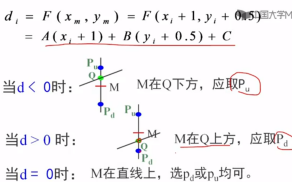
分析计算量？

两个乘法，四个加法，推导出d的增量公式

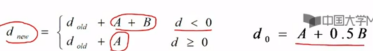d的初始值包含小数，因此可以用2d来代替d实现整数加法，所以d=2a+b

伪代码如下：

Void MidPointLine(int x0,int y0,int x1,int y1,int color){

Int a,b,delta1,delta2,d,x,y;

a=y0-y1;b=x1-x0;

d=2*a+b;

Delta1 = 2*a;

Delta2 =2*(a+b);

X = x0;

Y=y0;

//在对应的x,y像素点着色

putpixel(x,y,GREEN);

while(x<x1)

{

if(d<0)

{x++;y++;d+=delta2;}

else

{x++;d+=delta1;}

//在对应的x,y像素点着色

putpixel(x,y,GREEN);

}

Bresenham算法

每步的进化：

DDA把算法效率提高到每步只做一个加法

中点算法进一步把效率提高到每步只做一个整数加法

Bresenham算法提供了一个更一般的算法，该算法不仅有好的效率，而且有更广泛的适用范围

 

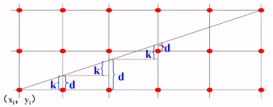
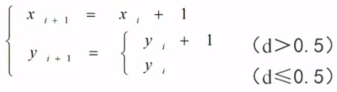
如何把算法的效率也提高到整数加法？

改进一：

令e=d-0.5

 

因为d的初值为0，

所以e的初值为-0.5，e=e+k,如果e>0,e=e-1

 

改进二：

 

在计算e值的情况下还是关于浮点数的计算，所以把浮点数化为整数。另外，k=dy/dx,再把dx取消，于是e`=e*2*△x,k`=k*2*△x

 

故e初=-△x,k=2*△y(要扩大多少倍，都扩大多少倍)，e=e+2*△y

 

如果e>0,e=e-2*△x

 

算法步骤为：

 

1. 输入直线的两端点P0（x0,y0）,P1(x1,y1).
2. 计算初始值，△x，△y，e=-△x,x=x0,y=y0.
3. 绘制点（x,y）
4. e更新为e+2△y,判断e的符号。若e>0,则(x,y)更新为(x+1,y+1),同时将e更新为e-2△x；

 

否则(x,y)更新为(x+1,y).

 

1. 当直线没有画完时，重复步骤3和4；否则结束。

 

伪代码如下：

 

Void BresenhamLine(int x0,int y0,int x1,int y1,int color){

 

Int e,x,y,dx,dy;

 

a=y0-y1;b=x1-x0;

 

e=-a;

 

X = x0;

 

Y=y0;

 

//在对应的x,y像素点着色

 

while(x<=x1)

 

{

 

putpixel(x,y,GREEN);

 

X++;

 

e+=2*dy;

 

if(e>=0)

 

{x++;y++;e-=-2a;}

 

//在对应的x,y像素点着色

 

putpixel(x,y,GREEN);

 

}

 

三种算法的总结：

 

DDA把算法效率提高到每步只做一个加法

 

中点算法进一步把效率提高到每步只做一个整数加法

 

Bresenham算法提供了一个更一般的算法，该算法不仅有好的效率，而且有更广泛的适用范围