【Leettcode】785.Is Graph Bipartite?二分图判断

There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:

存在一个 无向图 ，图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ，其中 graph[u] 是一个节点数组，由节点 u 的邻接节点组成。形式上，对于 graph[u] 中的每个 v ，都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性：

• There are no self-edges (graph[u] does not contain u).
• There are no parallel edges (graph[u] does not contain duplicate values).
• If v is in graph[u], then u is in graph[v] (the graph is undirected).
• The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.
• 不存在自环（graph[u] 不包含 u）。
  不存在平行边（graph[u] 不包含重复值）。
  如果 v 在 graph[u] 内，那么 u 也应该在 graph[v] 内（该图是无向图）
  这个图可能不是连通图，也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。

A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.

Return true if and only if it is bipartite.

二分图 定义：如果能将一个图的节点集合分割成两个独立的子集 A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为 二分图 。

如果图是二分图，返回 true ；否则，返回 false 。

 

Example 1:

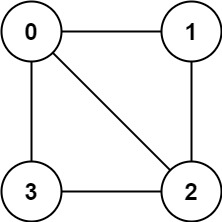
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.

解释：不能将节点分割成两个独立的子集，以使每条边都连通一个子集中的一个节点与另一个子集中的一个节点。

Example 2:

Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.

解释：可以将节点分成两组: {0, 2} 和 {1, 3} 。

Constraints:

• graph.length == n
• 1 <= n <= 100
• 0 <= graph[u].length < n
• 0 <= graph[u][i] <= n - 1
• graph[u] does not contain u.不会包含
• All the values of graph[u] are unique. 所有值互不相同
• If graph[u] contains v, then graph[v] contains u.

JAVA 广度优先搜索：

class Solution {
    public boolean isBipartite(int[][] graph) {
        //广度优先搜索
        //定义visited数组，初始值为0表示未被访问，1和-1表示两种不同的颜色
        int[] visited = new int[graph.length];
        //利用队列进行广度优先搜索
        Queue<Integer> queue = new LinkedList<>();
        //图中可能含有多个连通区域，需要判断是否存在顶点未被访问，若存在则从它开始再遍历
        for(int i=0;i<graph.length;i++){
            if(visited[i]!=0)
                continue;
            //i号结点未被访问过，入队
            queue.offer(i);
            visited[i] = 1;     //访问标记
            while(!queue.isEmpty()){
                int deQueue = queue.poll();   //队头结点出队
                for(int neighbor:graph[deQueue]){   //访问出队结点的邻接点
                    if(visited[deQueue]==visited[neighbor])
                        return false;   //邻接点颜色一致 不是二分图
                    if(visited[neighbor]==0){
                        visited[neighbor] = -visited[deQueue];  //与邻接点着相反颜色
                        queue.offer(neighbor);  //未访问的邻接点入队
                    }
                }
            }
        }
        return true;    //所有结点遍历完毕，未发现邻接点颜色一致，是二分图
    }
}

 JAVA 深度优先搜索：

class Solution {
    public boolean isBipartite(int[][] graph) {
        //深度优先搜索
        //定义visited数组，初值为0代表未访问，1和-1代表两种不同的着色
        int[] visited = new int[graph.length];
        //由于可能存在多个连通区域，需要遍历顶点邻接表
        for(int i=0;i<graph.length;i++){
            if(visited[i]==0 && !dfs(graph,i,1,visited))
                return false;
        }
        return true;
    }

    private boolean dfs(int[][] graph, int vertex, int color,int[] visited){
        //对某顶点vertex染色，先判断是否已染色
        if(visited[vertex]!=0){
            //判断已染的颜色与将染颜色是否一致，不一致则无法正确染色，返回false
            return visited[vertex] == color;   
        }
        
        //对当前顶点进行染色
        visited[vertex] = color;
        for(int neighbor:graph[vertex]){
            if(!dfs(graph,neighbor,-color,visited)){
                return false;
            }
        }
        return true;
    }
}