学习线段树总结
这几天在复习 qbxt 的知识,学到了线段树,就来总结一下。
线段树
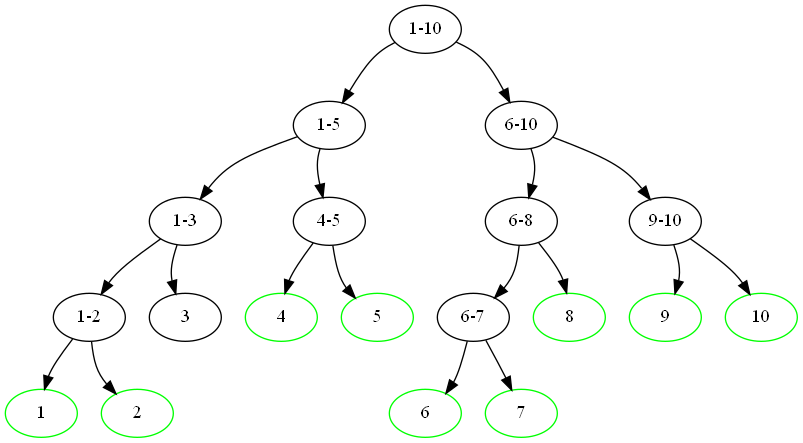
上面这张图显然是线段树,线段树就是一个处理区间的一个数据结构,将整个线段划分成一个树的结构,将长度不是 1 的段划分成两个子区间来求解,通过合并两个区间的信息来求解,这也是一个高效的数据结构。
总体时间复杂度为 \(\mathcal{O}(\log n)\)
- 适用范围:区间的最小值或最大值,区间的修改,区间求和
操作
在所有操作开始之前,可以观察到一个根节点为 \(p\) 的左儿子为 \(p^2\) ,右儿子为 \(p^2+1\)
inline int ls(int x){return x<<1;} // 左儿子 left sons
inline int rs(int x){return (x<<1)+1;} // 右儿子 right sons
建树
我们可以想到像树上 DFS 一样,可以一直访问儿子节点,直到儿子节点长度为 1 ,我们可以通过数据上的值去更改子节点的值,再有子节点来合并(更新)父节点的值。
void built(int l,int r,int p){
// 建树 [l,r] 为当前的区间,p 为当前的节点编号
lazy[p] = 1; // lazy_tag 后面会讲到
if(l == r){ // 如果 长度为 1
d[p] = a[l];
return;
}
int mid = l+(r-l)/2; // 递归求解
built(l,mid,ls(p));built(mid+1,r,rs(p));
d[p] = d[ls(p)] + d[rs(p)] ; // 由儿子更新父亲,合并
// 如果是求最大值,改成 d[p] = max(d[ls(p)],d[rs(p)]);最小值同样
}
区间查询
首先,我们可以想到还是像建树一样递归求解,如果这个区间在所要求的区间上了,直接返回,如果左儿子的子区间和原答案有交集,那么就递归到相应的节点上求解。那么思路就讲好了,代码怎么写呢?下面放上几张图就了解了
设所在区间为 \([l,r]\) , 查询区间为 \([s,t]\) 。

那么根据这张图可以很显然的推出所在区间在查询区间的判断方式:
if(s <= l && r <= t)
设中间位置为 \(mid = \dfrac{(l+r)}{2}\) 。
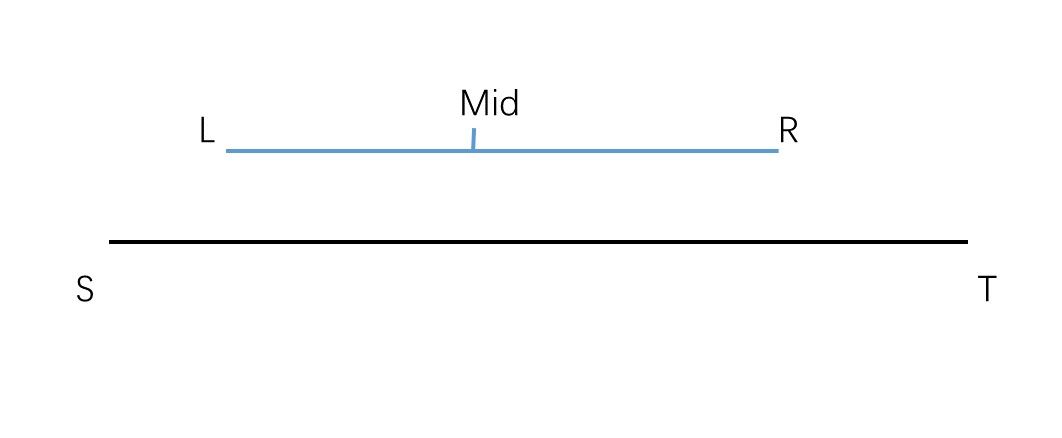
可以很简单的看出,进入左儿子的条件是:
if(mid >= s)
进入右儿子的条件是:
if(mid < t)
综上,我们可以得出查询代码:
LL query(int l,int r,int s,int t,int p){
// l,r 为当前的, s,t 为询问的
if(l>=s && r <= tt)
return d[p];
int mid = l+(r-l)/2;
pushdown(p,l,r);
LL sum = 0;
if(mid >= s)
sum += query(l,mid,s,t,ls(p)); // 如果是求最大值,就改成
// sum = max(quert(l,mid,s,t,ls(p)),sum); 最小值同样
if(tt > mid)
sum += query(mid+1,r,s,tt,rs(p));
return sum;
}
单点修改
在讲区间修改之前,我先来讲一下最基础的单点修改。单点修改也是递归找需要更改的点,然后再返回合并父节点的值
void update(int l,int r,int f,int c,int p){
// [l,r] 当前 p 节点的范围,f 是修改的点的编号, c 是修改的值
if(l == r){ // 如果递归到所达到的点了
d[p] = c;
// 如果是加上 c ,改成
// d[p] += c;
// 减去同理
return;
}
int mid = l + (r-l)/2;
if(mid >= f) // 如果所要修改的点在左儿子上,进入左儿子
update(l,mid,f,c,ls(p));
else
update(mid+1,r,f,c,rs(p));
d[p] = d[ls(p)] + d[rs(p)];
// 如果是求最大值,就改成
// d[p] = max(d[ls(p)] + d[rs(p)]);
// 最小值同理
return;
}
区间修改
-
懒标记
简单来说,就是通过延迟对节点信息的更改,从而减少可能不必要的操作次数。每次执行修改时,我们通过打标记的方法表明该节点对应的区间在某一次操作中被更改,但不更新该节点的子节点的信息。实质性的修改则在下一次访问带有标记的节点时才进行。
----- OI-Wiki
这段话深刻的阐释了懒标记的作用,如果不用懒标记时间复杂度将会达到 \(\mathcal{O}(n \log n)\) 有点慢,这样一来时间复杂度为 \(\mathcal{O}(\log n)\) 的。
听我这样一讲有点蒙先来看代码吧:
void update(int l,int r,int s,int tt,int c,int p){
// [l,r] 为当前的, [s,t] 为询问的
if(l >= s && r <= tt){
t[p] += (r-l+1)*c;lazy[p] += c //懒标记;
return;
}
int mid = l+(r-l)/2;
if(lazy[p] && l!=r){ // 懒标记的更新
t[ls(p)] += (mid-l+1)*lazy[p];t[rs(p)] += (r-mid) * lazy[p];
lazy[ls(p)] += lazy[p];lazy[rs(p)] += lazy[p];
lazy[p] = 0;
}
if(mid >= s)
update(l,mid,s,tt,c,ls(p));
if(tt > mid)
update(mid+1,r,s,tt,c,rs(p));
t[p] = t[ls(p)] + t[rs(p)];
}
举个例子吧:
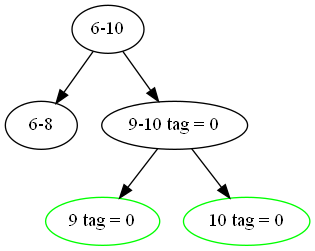
如果我想要更改 \([9,10]\) 的每个数加上 5,我们可以先直接在这个区间上改,并给它们打上标记。
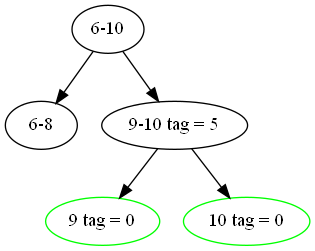
虽然,子节点没有更新值,但当我们要查询这两个子节点的信息时,我们会利用标记修改这两个子节点的信息,使查询的结果依旧准确。
现在,来查询一下 \([9,9]\) 的值,当递归到 \([9,10]\) 时,因为懒标记不为 0 ,所以将该区间的子区间更新并清零。
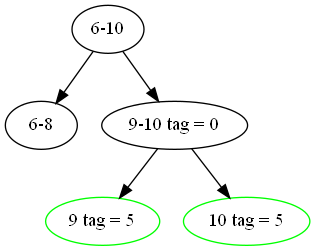
当然为了编写的简单性,修改懒标记可以写一个单独的函数 pushdown 。
带乘法的查询也同理,只是新加一个乘法懒标记而已
带懒标记的查询
LL query(int l,int r,int s,int tt,int p){
// l,r 为当前的, s,tt 为询问的
if(l>=s && r <= tt)
return t[p];
int mid = l+(r-l)/2;
if(lazy[p]){
t[ls(p)] += lazy[p] * (mid-l+1);t[rs(p)] += lazy[p] * (r-mid);
lazy[ls(p)] += lazy[p];lazy[rs(p)] += lazy[p];
lazy[p] = 0;
}
LL sum = 0;
if(mid >= s)
sum += query(l,mid,s,tt,ls(p));
// 如果是求最大值,就改成
// sum = max(quert(l,mid,s,t,ls(p)),sum); 最小值同理
if(tt > mid)
sum += query(mid+1,r,s,tt,rs(p));
return sum;
}
习题
基本上有了这些操作就可以写以下几道题目:
-
这道题是个纯模板题
-
这道题也差不多是个模板题,只是要注意:先乘后加 懒标记
-
单点修改的模板
-
单点修改,查询最大值的模板
-
HDU-1394 Minimum Inversion Number
线段树解决逆序对问题
-
POJ-3468 A Simple Problem with Integers
区间修改的模板题
模板题/好题未完待续 \(\dots \dots\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号