Lidar-Camera 联合标定算法

目录

• 初始参数求解
  • 2D雷达标定
  • 3D雷达标定
• 参数优化
  • 系统可观性
  • 充分旋转标定板

核心参考：旷视科技的知乎专栏-实践之Camera-Lidar标定
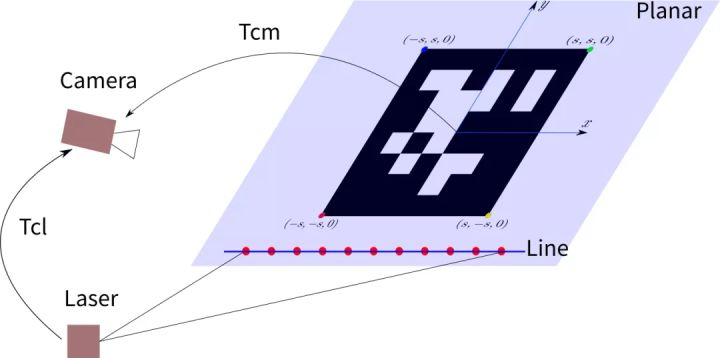
需要标定相机内参+相机&LiDAR外参，约束方法分为两种

方案	内容	备注
3D-3D	利用激光测量的三维激光点+相机测量的标定板三维坐标	本文讲解
3D-2D	利用激光测量的三维激光点+相机测量的图像二维特征（点特征，线段特征）	类似于多目摄像机的PnP算法，PnL

标定过程的通常做法是先利用少量观测求解外参数的初始值，然后利用多帧数据的约束进行最小二乘优化对初始值进行 refine

初始参数求解

假设标定板平面在相机坐标系 \(c\) 中的参数为 \(\pi ^ { c } = [ n ^ { c } , d ] \in \mathbb{R} ^ { 4 }\) ，其中 \(n^c \in \mathbb{R}^3\) 是平面的三维法向量， \(d\) 是相机坐标系原点到平面的距离。平面上的一个三维点在相机坐标系下的坐标为 \(P^c \in \mathbb{R}^3\) ，点在平面上满足：

\[n ^ { c ^{T} } P ^ { c } + d = 0 \]

\[P ^ { c } = R _ { cl }P ^ { l } + t _ {cl} \]

假设从激光坐标系 \(l\) 到相机坐标系之间的旋转和平移为 \(R_{cl}=R_{3\times 3}\) , \(t_{cl}=t_{3\times 1}\) 。如果知道激光坐标系中某个激光点 \(P^l\) 落在标定板上，则通过点在平面上这个约束能够构建关于外参数的方程：

\[n ^ { c ^{T} } ( R _ { c l } P ^ { l } + t _ { cl } ) + d ^ { c } = 0 \]

上述方程能够提供一个约束，通过多个这样的约束就能求解外参数。求解时，一个直观的想法是利用 g2o 或者 ceres 等优化工具构建非线性最小二乘进行优化求解。但是对于非线性最小二乘问题，需要知道外参数的一个初始值，如果初始值不准确，则有可能会优化到局部最小值。因此，一个合理的求解流程应该是闭式解提供初始值，对该初始值利用多帧数据进行优化，得到更准确的标定结果。
虽然平面约束对于 2D 激光和 3D 激光而言是一样的，但 2D 激光和 3D 激光闭式求解外参数的方式稍有不同。因为 3D 激光的激光点更多，从而可以直接计算激光点云的法向量，利用这个法向量简化外参数计算流程。

2D雷达标定

激光点从LiDAR坐标系到Camera坐标系公式为

\[P ^ { c } = R ^T_ { l c } ( P ^ { l } - t _ { lc } ) \]

考虑到，激光为 2D 激光，激光束形成的平面不妨假设为 xy 平面，即 \(z=0\) ，此时有 \(P^l=[ x , y , 0 ] ^ { T }\)，上式整理为

\[P ^ { c } = R ^T_ { l c } ( \left[ \begin{array} { l } { x } \\ { y } \\ { 0 } \end{array} \right] - t _ { t c } ) = R^T _ { l c } \left[ \begin{array} { l } { 1 } & { 0 } \\ { 0 } & { 1 } & { - t _ { c } } \\ { 0 } & { 0 } \end{array} \right] \left[ \begin{array} { l } { x } \\ { y } \\ { 1 } \end{array} \right]=H \hat{P}^l \]

\(H\) 具有9个参数，2D雷达具有2个约束，因此需要5组点得到基本数据 \(R^T_{lc}\)和\(t_c\)
P.S. \(R_{cl}\)为正交矩阵，因此需要进行正交化（Frobenious Norm）

3D雷达标定

在3D的情况下，输入不再是点，而是平面，对前方程进行改造可以得到如下公式 (式一不再存在位移t)

\[R _ { c l} n ^ { l } = n ^ { c } \]

\[n ^ { c ^{T} } ( R _ { c l } P ^ { l } + t _ { cl } ) + d ^ { c } = 0 \]

我们发现上式只与\(R _ { c l }\)有关，下式与\(R _ { c l }, t_{cl}\)有关，所以优先解决上式。由上式可得最小二乘模式

\[C=\sum_{i=1}^{N}||n_{i}^{c}-R_{cl}n_{i}^{l}||^{2}=\sum_{i=1}^{N}(n_{i}^{c}-R_{cl}n_{i}^{l})^{T}(n_{i}^{c}-R_{cl}n_{i}^{l})=\sum_{i=1}^{N}(n_{i}^{c^{T}}n_{i}^{c}+n_{i}^{l^{T}}n_{i}^{l}-2n_{i}^{c^{T}}R_{cl}n_{i}^{l}) \]

因为其他的因式都是确定的，为了让整体最小，就要关注其中的这个因式，希望它能够取到最大值

\[F=\sum_{i=1}^{N}n_{i}^{c^{T}}R_{cl}n_{i}^{l} \]

因为\(n_{1\times3}·R_{3\times3}·n_{3\times1}\)得到的是\(1\times1\)矩阵，一定等于自身的Trace，而Trace具有回转平移的性质，即\(\operatorname{Trace}(ABC)=\operatorname{Trace}(BCA)=\operatorname{Trace}(CAB)\)，因此有

\[F=\operatorname{Trace}(\sum_{i=1}^{N}n_{i}^{c^{T}}R_{cl}n_{i}^{l})=\operatorname{Trace}(\sum_{i=1}^{N}R_{cl}n_{i}^{l}n_{i}^{c^{T}})=\operatorname{Trace}(R_{cl}·\sum_{i=1}^{N}n_{i}^{l}n_{i}^{c^{T}})=\operatorname{Trace}(R_{cl}H) \]

对H进行SVD分解，可以得到\(H=UAV^{T}\)，其中\(U\)和\(V\)为\(3\times 3\)正定矩阵，\(V\)为\(3\times 3\)非负对角阵。而由某定理可知，\(R_{cl}\)应为\(R_{cl}=VU^{T}\)。得到\(R_{cl}\)后，带入下式可以用最小二乘法计算\(t_{cl}\)

\[P^{c}=R_{cl}P^{l}+t_{cl} \]

参数优化

使用LM算法进行优化（我的博客LM算法）
参数化使用\(SO_3\)或者四元数，可以查看博客旋转矩阵&四元数

\[\hat{R_{cl}},\hat{t_{cl}}=\arg\min_{R_{cl},t_{cl}}\sum_{i=1}^{N}\frac{1}{N_{i}}\sum_{m=1}^{Ni}||n_{i}^{c^{T}}(R_{cl}P_{im}^{l}+t_{cl})+d_{i}^{c}||^{2} \]

利用标定板边缘直线约束来标定3D激光^[1]；

对2D激光的多种标定板的有效约束的讨论^[2]

同时，把激光的点想象成一个采样方式，2D激光就是确定一条线，对线进行采样，从这一群点能够还原得到一条最置信的线，而这个线对平面的约束只有2。同理，3D激光就是一个面，对面进行采样，从这群点能够得到一个最置信的平面，而这个面的约束有3。

系统可观性

参考文献^[3]的第二章

TODO 没看懂

充分旋转标定板

既然采集数据时只平移标定板不行，那是否意味着简单旋转一下标定板就可以了呢？比如标定板只绕着 y 轴旋转。这里可通过设置不同的旋转矩阵去验证 H 矩阵是否有零空间。通过简单修改代码（注释或反注释设置旋转矩阵的那几行代码），运行后会发现：标定时需要充分旋转 x 和 y 两个轴，标定过程中标定板只旋转一个轴一样会存在零空间基底。

这意味着拿着标定板旋转时，需要充分旋转 roll 和 pitch。更直白一点，假设在长方形的标定板中心画了个十字线，那请绕着十字线的两个轴充分旋转，比如绕着竖轴旋转，然后还要绕着横轴旋转。

---

1. Automatic Extrinsic Calibration of a Camera and a 3D LiDAR using Line and Plane Correspondences,arXiv ↩︎

2. Wenbo Dong, A Novel Method for the Extrinsic Calibration of a 2D Laser Rangefinder and a Camera,arXiv ↩︎

3. 8 ↩︎