拓扑排序
根据所给的有向图给出一个按照特定顺序排序的序列，对于任意两个点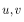
如果在他们之间存在一条路径，则u必须在v的前面。
- BFS
- DFS
BFS求解
step1.首先把所有入度为0的节点放入队列中
step2.若队非空，则每一次取出一个节点放入到序列中
step3.将该节点所有出度节点的入度-1（我们可以想象成把原来那个节点给删除了）
step4.检查所有出度节点的入度是否为0，若为0，则放入队列中
step5.返回第2步
最后我们就得到了一个拓扑排序序列
伪代码：
DFS求解
对于所给的有向无环图，我们对所有点进行DFS，并按照完成时间进行排序。随后我们逆序输出该序列获得逻辑序列。
正确性证明：
对于任意一条边<u,v>,其中u在v前面，我们要保证他们的完成时间f(u)和f(v)满足f(u)>f(v)。此时我们按照所给形式进行从u到v进行搜索，有以下几种情况：
1.v未被搜索，那么最后的完成时间一定是f(u)>f(v)
2.v未被搜索，那么此时u未被完成，最后的完成时间满足f(u)>f(v)
3。v正在被处理，并不存在这种情况，否则存在一条环路，与题目要求不符
综上所述，该方法可行。
下面给出伪代码
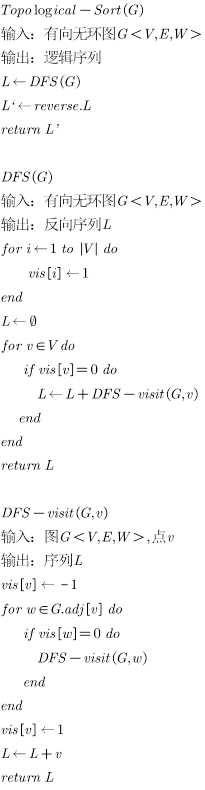
强连通分量检测
定义：
1.强连通分量是顶点的子集
2.强连通分量的内部相互可达
3.额外增加任意一个顶点，不保证相互可达
算法设计：
第一步：将图上所有的边反转，获得反向图。
第二步：在上进行DFS，并按照完成时间获得序列L
第三步：按照L相反的顺序进行DFS，得到强连通分量
伪代码：
正确性证明：
我们令每一个强连通分量为一个点，则可以得到一个新的有向图
该有向图性质如下：
1.至少存在一个点满足出度为0
2.删除每个出度为0的点后，总存在新的出度为0的点
证明：
对于1，若不满足，则该有向图存在环。则不符合强联通分量的最大性
对于2，若不满足，则该有向图的子图存在环。
而对于第二次DFS而言，我们发现他的搜索循序按照出度为0的点的顺序搜索
证明：
先讨论第一次的DFS搜索，对于在反向图里面的强连通分量u和v，且存在一条从u到v的路径。则必定有f(u)>f(v)。即在L序列里面，u出现在v的后面。
而对于第二次的DFS，由于采用L逆序搜索，我们先搜索u，而此时有从v到u的路径。所以符合我们上面给出的搜索顺序。
又因为对于每一个出度为0的点（我们回归到强连通分量进行分析）DFS不仅可以将它内部所有的点都搜索一遍。还因为出度为0，所以不会将非该强连通分量的点搜索。所以算法成立。
最小生成树
- prim算法
- kruskal算法
Prim算法
算法思想：
首先引入一个问题：众所周知kc是个懒b，他平时会出没在如下地方：宿舍，宿舍的床上，新主楼（被迫组会），篮球场，教学楼。现在我们希望在这五个地方修建一些kc专属路径保证kc可以在任意两个地方间穿梭（虽然他平时都是在床上就完成了所有的事情）。我们会告诉你每两个地方修建所需欢乐豆（然而kc并不会打斗地主），请你给出一个花费欢乐豆最少的方案。
针对这个问题，我们可以进行如下建模。我们把宿舍，宿舍的床，新主楼，篮球场和教学楼抽象成一个个节点。另一方面，我们把在两个地方之间的专属路径抽象成一条边，修建该边所花费欢乐豆抽象成该边的权。所以此时转化成F228（kc上算法课（打游戏睡觉吃早饭吃午饭吃下午茶吃晚饭吃夜宵刷牙洗脸洗澡泡澡冲澡 ）学习算法的地方）地区方言即为：我们要找到给定图的最小生成树。
具体怎么实现呢，我们先看看对于最小生成树有什么特性：
对于割集(A,V-A)，我们称横跨该割权值最小的边为轻边。则轻边一定属于一个最小生成树。接下来给出证明：假设结论不成立，那么该轻边不属于任何一个最小生成树。根据最小生成树的定义，我们一定有另一条(x,y)边属于一个最小生成树且横跨该割，且w(x,y)>w(u,v)。那么包含边(x,y)的最小生成树加上边（u,v）后形成环路。此时去除边(x,y)，添加边(u,v)，形成另一个生成树。则w(T')=w(T)-w(x,y)+w(u,v)。由于w(x,y）<w(u,v)，则w(T')>w(T)。说明（x,y）不属于任何一个最小生成树。原命题得证。
根据这个性质，我们有如下启发：面对于两个集合：形成生成树的集合和待形成生成树的集合。我们选用他们之间权重最小的那条边，以此类推。或者说，那条边代表着两个集合最短的距离。我们每次都选用这个最短的距离，从而形成一个最小生成树。
根据上面的讨论，我们可以得到如下策略：
step1:给出基点，规定基点的距离为0。
step2:检测所有点是否都完成，若不是，则选出所有点中距离生成树点集中距离最小的点，并记录该点的前驱节点
step3:根据选出点，更新所有点到该点的距离
step4:标记该点为已完成点。回到step2。
下面给出伪代码
输入：图G=<V,E,W>
输出：最小生成树L
时间复杂度分析：我们将整个的过程分为三个大部分，初始化阶段，节点选择阶段与节点更新阶段。
对于初始化阶段，显而易见时间复杂度为O(V)。对于节点选择阶段和节点更新阶段，我们先看对于每一次来讲，节点选择的时间复杂度为O(V),节点更新的时间复杂度为O（deg(u)），对于二者每一次的总时间复杂度为O(V+deg(u))。对于V次的遍历，二者的总时间复杂度为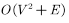
。那么总的时间复杂度为
。
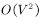事情看似到此为止了，kc同学也可以安心的躺在床上开组会了（bushi）。但平方是一个很恶心的东西，它会坐飞机到带火的评测数据上，疯狂打出TLE。那么有什么方法可以进行优化呢？
我们发现，貌似比较浪费生命的地方在于寻找出最小距离那里，我们需要遍历所有的节点去得到最后的最小值。但是根据祸不及家人的原则，为什么因为数据存储的形式并非最优从而损害了总的时间复杂度？所以说不妨换一种数据结构，让查找最小值变得更方便。
Entertainment time:什么数据结构可以让查找最小值变得更方便？猜猜我是谁？
ok兄弟们，全体目光向我看齐，看我看我，我宣布个事！我是个优先队列！
所以便有了如下的改进形式：
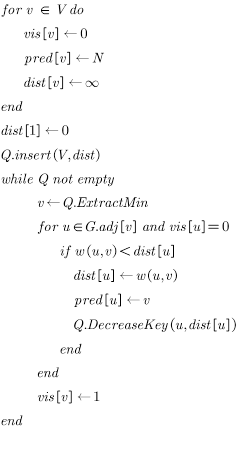
这次我们采用优先队列的方式去存储节点信息，这么看虽然我们损失了一定的时间去修改，但是我们减少了寻找最小值边所需要的时间。我们接下来来具体分析
首先初始化的时间复杂度为O(|V|),之后我们在选择与更新阶段，我们先分析每一次的时间复杂度，可见每一次的选择阶段为O(logV)，每一次的更新时间复杂度为O(deg(u)logV)。那么总的选择时间复杂度为O(VlogV)，更新时间复杂度为O(|E|log|V|),综上，总的时间复杂度为O(|E|log|V|)。
kc同学在得到了你的prim后非常兴奋，同时在从宿舍到新主楼的路上把人家车撞了一个坑，被人家找上门了（悲伤的故事&&具体数学背大锅）
kruskal算法
算法思想：
我们继续上面讨论的最小生成树问题。除了Prim算法外，还有一种处理方式叫Kruskal算法。该算法采用另一套体系。想称为最小生成树の王のKruskal想：既然我要做的是总权值最小的生成树。那为什么不能每次取出最小的边权值呢？另一方面，为了防止最后像-OH和-H一样成环（好像是吧我也忘了）他在每做一次取边时都要检查是否会成环。多多重复，百炼成钢！最终，他得到了一个最小生成树！Words can not express how exciting he is!(六级前夕写下，不过我忘了报了)
那么这么做一定能保证每次取到的边都是同一个最小生成树的边吗？下面给出相关证明：
原有的边集A将原图分为了很多个子树，此时我们选择了一条权值最小且使得原树不成环的边L（x,y）。且L横跨割（ V’ , V-V’ ）。根据我们上面Prim算法中同样的证明，该边与A同属于一个最小生成树的子集。
此时我们知道我们应该怎么做了：
我们此时已经完成第一步了，接下来的问题是：如何高效且准确的判断两个节点是否在同一个子树下以及如何合并子树？
不急，为了解决这个问题，我们引入一个新的数据结构：并查集（恭喜，你的禅境花园多了一株新的植物）
并查集表示的是元素的所属。比如忍界大战中为了证明自己的身份就可以穿着任何一个村的村服。这样在战场中就自动分为了五个集合。每个元素属于一个集合（假如没有谁睡过头了忘穿衣服就来发动忍术了）。而在平时和平时期也可以说自己是根的部下，往根上一查哦原来是木叶村的组织。从而也将它自动归为了木叶村这个集合。
这两种方式其实说明了并查集的两种实现方式。第一种是每个元素记录自己的根节点。第二种则是记录自己的父节点。两种形式的根节点均记录自己。不用情况下两种方式各有利弊，
（后续出了并查集教程会细说）在Kruskal算法中，我们采用记录父节点的方式。
那么此时，我们来着手这两个问题：
1.如何验证两个节点在不在同一个子树下？
答案显而易见，对于两个节点我们只需要网上一步一步的查找父节点，直到查找到二者的根节点。此时若根节点相同，则在同一子树下，反之则不在。
下面给出查找根节点的伪代码
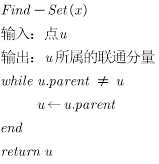
2.如何合并两个节点？
方法一：我们可以直接把一个节点作为另一个节点的父节点。但是这么做我们再进行查找时所消耗的时间增多。
方案二：我们把一个节点的根节点作为另一个节点根结点的子结点。为了保证查找效率，我们将树高小的树安插在树高高的树的下面。
综上所述，我们采用方案二的实现方式
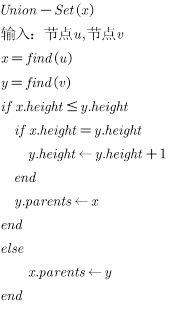
此外，我们还需要创建并查集，那么初始状态下他们应该各自为政，即
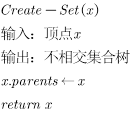
根据以上介绍，我们最终得到了kruskal算法的最终形态
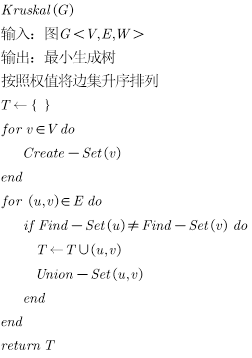
时间复杂度分析
首先给出Create-Set(x),Find-Set(x),Union-Set(x)的时间复杂度：
Create-Set(x)=O(1)
Find-Set(x)=O(h)
Union-Set(x)=O(h)
其中，h为树高，那么h和节点数V有什么关系呢？
通过数学归纳法可以证得：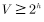
所以
Create-Set(x)=O(1)
Find-Set(x)=O(log|V|)
Union-Set(x)=O(log|V|)
接下来进行整体分析:对于初始化阶段，我们所需要的时间为排序O(|E|log|E|),创建并查集O(|V|),对于查找&&合并树阶段，每一次的时间复杂度为O(log|V|)+O(log|V|)=O(log|V|)所以合并树阶段总的时间复杂度为O(|E|log|V|)。又有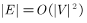
,所以总的时间复杂度为O(|E|log|V|),和Prim算法一样
单源最短路径
- Dijkstra
- Bellman-Ford
Dijkstra
算法思想：
单元最短路径问题是为了解决求一个点到所有点的最短路径问题。我们之前谈过可以用BFS解决这种问题。具体做法是先搜索具体目标点为1的点，再搜索距离目标点为2的点…以此类推，直到更新完所有的节点。但是使用BFS的前提条件为每个边都是等价的，及该图为无权图。那么面对有权图（网络）时，我们就需要改变算法。这里，我们使用Dijkstra算法。
该算法的思想如下：对于任意一个节点a，它有对原点s的实际最小距离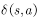
，同时我们对它到原点的最小距离有一个估计距离dist[u]。每次我们取估计距离最小的那个节点并确定该估计距离为实际最小距离。然后更新与该点联通节点的估计距离，以此完成所有点的更新。
那么这时候就有人要素察觉了，为什么你找到的估计距离最小的点就是实际最小距离呢？下面给出证明：
对于第一个除了原点以外的点的查找与更新，该算法必然成立
我们假设第m个节点依然成立，而到了第m+1个节点时，该方法找到的节点u并非最短路径，即。此时必定存在另一条最短路径<s…x,y….u>，其中边（x,y）横跨已查询最短路径节点集合与其他节点集合。
对于该路径为到u的最短路径，那么<s…x,y>必定为到y的最短路径。那么此时有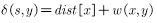
同时y已经完成了松弛操作，所以有
综上，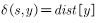
。此时有
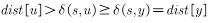,而我们的算法每次只选取距离最短的点，所以我们不会去选u，而是去选y。综上所述，第m+1个点依然成立，故算法成立。
其实上面的论述也很好说明了为什么Dijkstra只支持边权非负。当边权为负数时上述讨论中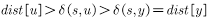
性质不成立，因为y到u间可能存在负边的情况，故只支持边权为正值时。
下面给出伪代码
时间复杂度分析:初始化阶段为O(|V|)，接下来循环|V|次，对于每一次的循环，查找最小边阶段为O(|V|),更新阶段为O(deg(u))那么总的时间复杂度为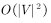
。
类似的，我们可以利用优先队列对查找阶段进行优化
时间复杂度分析：初始化阶段的时间复杂度为O(|V|)+O(|V|log|V|),对于每一步的操作，搜索时间复杂度为O(log|V|),更新的时间复杂度为O(deg(u)log|V|)。那么总的搜索时间复杂度为O(|V|log|V|),总的更新时间复杂度为O(|E|log|V|)。又有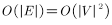
，故总的时间复杂度为O(|E|log|V|)
Bellman-Ford
上面已经讨论了当权值不全为正的时候不可以使用Dijkstra。也就是说我们需要应用另外一种策略来完成最短路径的查询，由此引出Bellman-Ford算法。
对于权值不全为正的图，我们延续原来的松弛操作，只不过这次我们每一次都要进行所有边的松弛，直到所有的点都松弛不动为止。注意，我们还应考虑一个问题：边权含有负值的有向环，在一定情况下该环会无限制的松弛下去。所以我们需要去解决两个问题：
- 如何去对所有边进行松弛
- 如何找出无限松弛下去的有向环
对于第一个问题我们很好解释，只要每一次都对所有边依次做松弛即可。而对于第二个问题，我们也有了对应的解决办法。只需要设置一个临界值，当超过这个临界值却依然还在松弛，我们就可以判定它是可以无限松弛下去的负环。但是怎么去规定这个值，既能保证在规定遍历结束后所有点都处于最短路径的同时，还尽可能的小？
通过推理发现对于任何一个给定源头可达的点，我总存在一条简单路径（这条路径不会大于|V|-1）。所以我最大需要|V|-1次循环来完成所有点的更新，这就是我们需要的临界值。
下面给出伪代码：
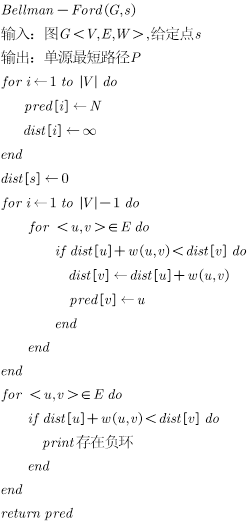
最后我们来分析一下时间复杂度：对于初始化阶段时间复杂度为O(|V|)，对于更新阶段时间复杂度为O(|E||V|)，最后对于检测阶段时间复杂度为O(|E|)。所以总的时间复杂度为O(|V||E|)
浙公网安备 33010602011771号