【学习笔记】【算法】FHQ-Treap

部分改编自此文。

听说 FHQ-Treap 完爆 Splay，不知道是不是真的（

定义

Treap，即二叉搜索树（BST）+ 堆（Heap）。

Treap 主要维护的东西有两个：

权值 \(val\)，利用此生成 BST。
随机值 \(rnd\)，利用此生成 Heap。

本算法相比 BST 的精妙之处就在于，添加了堆使得 BST 实现随机平衡，从而实现理论复杂度。

FHQ-Treap 的主要功能为：

分裂：按照 \(val\) 将一颗树分裂为两颗。
合并：按照 \(rnd\) 将两棵树合并成一颗。

其他功能全部是基于这两种基本操作的。

本文中的 Heap 维护的是小根堆。

然后让我们直入正题。

核心操作

定义

const int N = 10005;

struct node{
    int l, r;  // 左右孩子
    int val;   // BST 的权值
    int rnd;   // Heap 的随机值
    int size;  // 此树的大小
} t[N];

int root = 0, n = 0;  // 根节点, 最新节点的下标

当然不一定只有这几个，只是这几个是必需的。

newnode

顾名思义，就是创建一个新的点。

inline int newnode(int v=0)
{
	tot++;
	t[tot].val=v;
	t[tot].rnd=rand();
	t[tot].size=1;
	return tot;
}

此处如果函数不填值则默认为 \(0\)，返回量为新点的编号。

pushup（不是俯卧撑）

主要功能为上传维护 \(size\)。

inline void pushup(int k) {
    t[k].size = t[t[k].l].size + t[t[k].r].size + 1;
}

与大多数的 pushup 相同，是在回溯时进行操作，同时也不止可以维护 \(size\)，具体看题目要求。

pushdown 因为不是必需所以没写，但操作时间也是下搜前，维护的东西也要在场上看，在这里就不细讲了。

分裂 split

温馨提示：不要打成 spilt（

函数为 split(int k,int v,int &x,int &y)。其中 \(k\) 为当前点，\(v\) 为分裂时所需的数值，\(x\) 为分裂出的左树的根节点，\(y\) 为分裂出的右树的根节点，左树和右树都为 Treap，并且所有在左树上的节点的 \(val\) 必须全部小于右树上的 \(val\)。一般分裂有两种，按照分裂出的树规定的大小来分裂以及按照 \(val\) 来分裂。

我们先讲第一种，即规定分裂的树的大小。此处默认规定的为左树。我们的目标为：将这棵树拆成两颗，并且使左树的 \(size=v\)。假如目前搜到的节点为 \(u\)，则有两种情况：

若左子树的 \(size\) 为不大于 \(k\)，那说明我们要分裂出的左树会把 \(u\) 的整个左子树和当前点都包括。那么就要使 \(x=k\)，并向下搜索右子树，使搜到的新 \(x\) 成为 \(u\) 的右儿子。代码为 x=k,split(t[k].r,v-t[t[k].l].size-1,t[k].r,y)。要注意 \(v\) 要减去左子树和 \(u\) 的 \(size\)。
若左子树的 \(size\) 为大于 \(k\)，那说明我们要分裂出的左树会在 \(u\) 的左子树之中。那么就要使 \(y=k\)，并向下搜索左子树，使搜到的新 \(y\) 成为 \(u\) 的左儿子。代码为 y=k,split(t[k].l,v,x,t[k].l)。

附完整代码：

void split(int k, int v, int &x, int &y) {
	if (!k) {
		x = y = 0;
		return;
	}
	pushdown(k);
	if (t[t[k].l].size < k) {
		x = k;
		split(t[k].r, v - t[t[k].l].size - 1, t[k].r, y);
	} else {
		y = k;
		split(t[k].l, v, x, t[k].l);
	}
	pushup(k);
}

接下来是第二种，即按 \(val\) 来分裂。我们的目标为，左树的所有点的 \(val\) 皆不大于 \(v\)。同样两种情况：

若 \(u\) 的 \(val\) 不大于 \(v\)，则说明整个左子树的值都小于 \(v\)。那么就使 \(x=k\)，然后继续往右子树找就好了。大体与第一种差不多。
若 \(u\) 的 \(val\) 小于 \(v\)，与第一种情况一样处理，就不赘述了。

附完整代码：

void split(int k, int v, int &x, int &y) {
	if (!k) {
		x = y = 0;
		return;
	}
	pushdown(k);
	if (t[k].val <= k) {
		x = k;
		split(t[k].r, v, t[k].r, y);
	} else {
		y = k;
		split(t[k].l, v, x, t[k].l);
	}
	pushup(k);
}

第二种分裂操作的动态示意图如下：

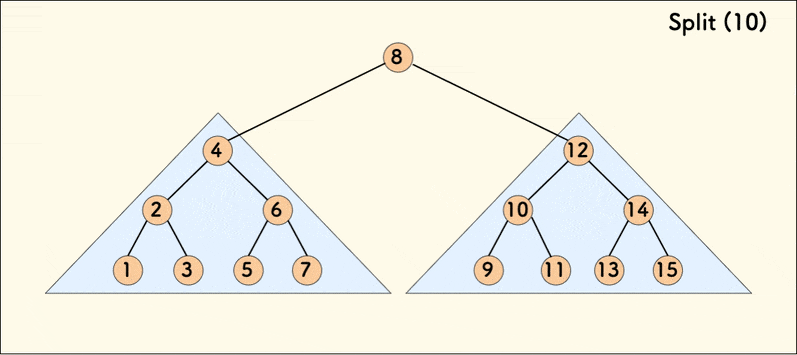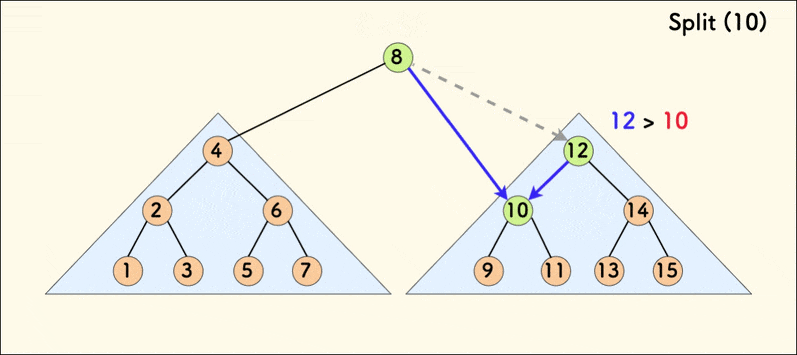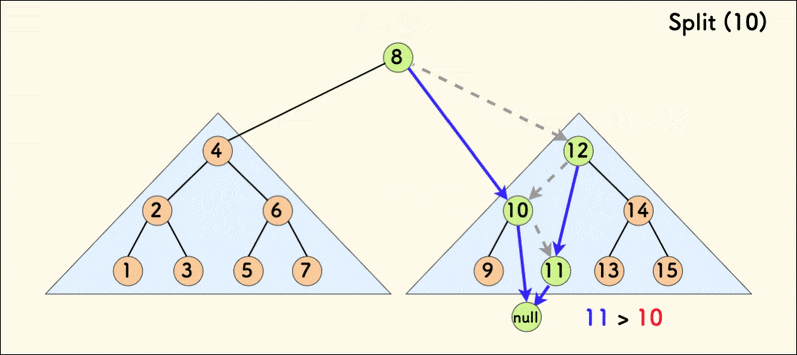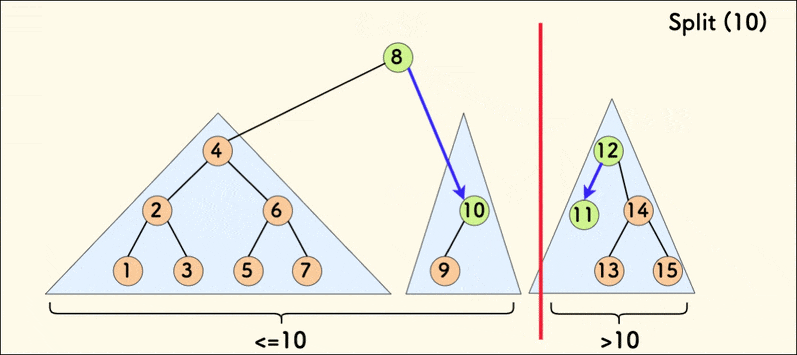
若树是相对平衡的，则 split 操作的时间复杂度为 \(O(n \log n)\)。

当然，很重要的一点是，split 操作不会改变树的中序遍历。想证明也很简单，假设 \(u\) 的右儿子从原来的右儿子变成了指向一个新的 \(x\)，可 \(x\) 本就来源于 \(u\) 的右子树，因此二者在中序遍历上的相对位置没有改变。这对于所有点都适用，既然没有相对位置被改变，那么中序遍历也就没被改变。如图：

合并 merge

合并就只有一种了。

合并函数为 merge(int x,int y)，含义为：合并 \(x\) 与 \(y\) 两颗 Treap，形成一颗新 Treap，并返回新 Treap 的根的下标。

合并的前提为 \(x\) 中的所有 \(val\) 皆小于 \(y\)。

先给出代码：

int merge(int x, int y) {
    if (!x || !y) return x + y;
    if (t[x].rnd < t[y].rnd) {
        t[x].r = merge(t[x].r, y);
        pushup(x);
        return x;
    } else {
        t[y].l = merge(x, t[y].l);
        pushup(y);
        return y;
    }
}

然后进行解释。这里就给出第一个 if 的解释，第二个也可以推出来。

既然 \(x\) 的 \(rnd\) 比 \(y\) 小，所以对于此处的合并，要让 \(x\) 作为新树的新根。既然 \(y\) 的 \(val\) 比 \(x\) 大，那么就要让 \(y\) 成为 \(x\) 右子树的一部分。因此继续让 \(y\) 与 \(x\) 的右子树合并，形成 \(x\) 的新右子树。

\(x\) 的 \(rnd\) 比 \(y\) 大的情况同理，不多说了。

值得注意的是，\(y\) 能和 \(x\) 的右子树合并，也满足了 \(val\) 皆小于 \(y\) 这一性质。

附动态示意图：

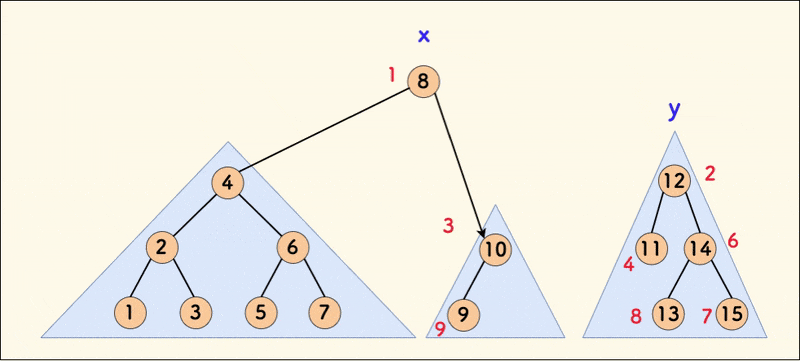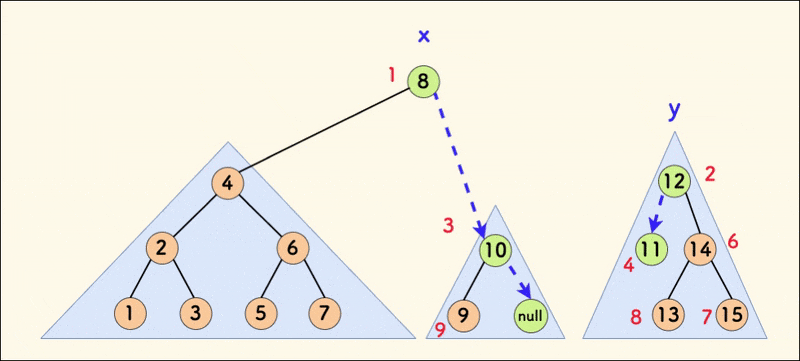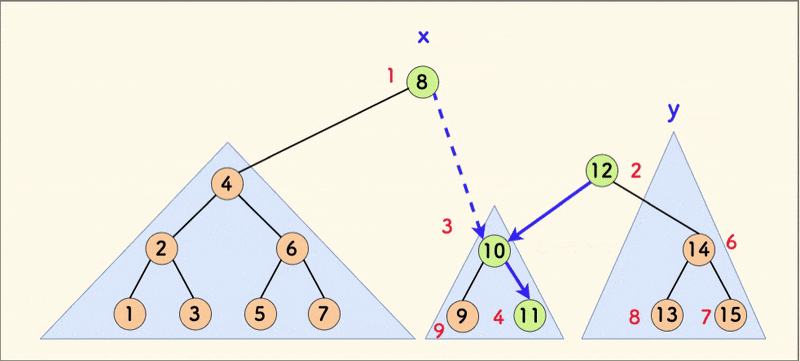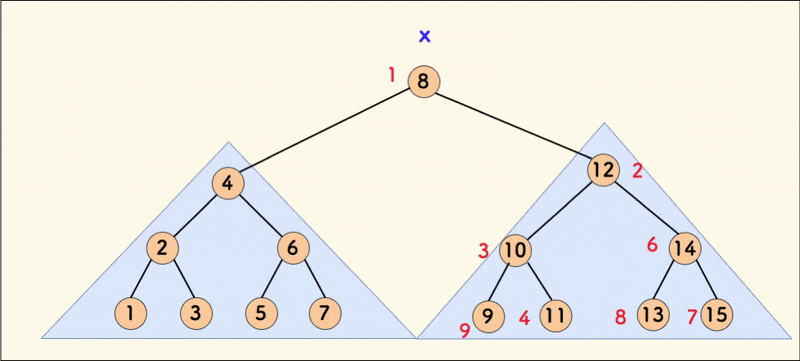
若树是相对平衡的，则 merge 操作的时间复杂度为 \(O(n \log n)\)。

同样，merge 操作不会影响中序遍历，与 split 是一个道理。

常用操作

插入 insert

插入一个大小为 \(v\) 的节点，需要以下三步：

将现在的 Treap 按照 \(v\) 分开。
生成一个新的 \(val\) 为 \(v\) 的点，将其也视为一个 Treap。
将这三个 Treap 合并。

不过，合并前提为 \(x\) 中的所有 \(val\) 皆小于 \(y\) 这一条不要忘掉。

附出代码：

void insert(int v) {
    int x, y;
    split(root, v, x, y);
    int z = newnode(v);
    root = merge(merge(x, z), y);
}

删除 del

与 insert 是一个道理，只是反过来，就不过多解释了。

void del(int v) {
    int x, y, z;
    split(root, v, x, z);
    split(x, v - 1, x, y);
    y = merge(t[y].l, t[y].r);
    root = merge(merge(x, y), z);
}

排名 rnk

即返回权值 \(v\) 在树中的排名。通俗点讲，就是小于 \(v\) 的数 \(+1\)。

只需要按照 \(v-1\) 分裂出左子树 \(x\)，答案就是 \(x.size+1\)。

搞完再合并回去就行了。

int rnk(int v) {
    int x = 0, y = 0;
    split(root, v - 1, x, y);
    int ans = t[x].size + 1;
    root = merge(x, y);
    return ans;
}

第 p 小 topk

即查找第 p 小的权值。

利用二叉搜索树的性质，若此点左子树的 \(size\) 恰好为 \(p-1\)，那么此点就是第 \(p\) 小。否则比 \(p-1\) 大往左子树搜，比 \(p-1\) 小往右子树搜第 \(p-左子树.size-1\) 小的点。

int topk(int k, int p) {
    int ls = t[t[k].l].size;
    if (p-1 == ls) return t[k].val;
    if (p-1 < ls) return topk(t[k].l, p);
    return topk(t[k].r, p - ls - 1);
}

前驱，后继

前驱函数 get_pre(v) 的含义是：找出树中严格小于 v 的最接近的权值。

后继函数 get_suc(v) 的含义是：找出树中严格大于 v 的最接近的权值。

这里讲解一下前驱函数。

只要按 \(v-1\) 分裂子树，然后在分裂出的 \(x\) 上查找 topk(x,t[x].size)，就是前驱的答案。

后继也是一样的，就不说了。

代码：

int get_pre(int v) {
    int x = 0, y = 0;
    split(root, v - 1, x, y);
    int ans = topk(x, t[x].size);
    root = merge(x, y);
    return ans;
}
int get_suc(int v) {
    int x = 0, y = 0;
    split(root, v, x, y);
    int ans = topk(y, 1);
    root = merge(x, y);
    return ans;
}

那么基础的部分就写完了。

可持久化 FHQ-Treap

看着很简单，实则也不难（

以 Luogu P3835 为例。

可以发现需要保存版本的只有 split 和 merge 操作。

那我们只需要在 split 和 merge 进行操作时给他开个新点来保存就可以了，这样就实现了可持久化！

具体看下面的代码：

void split(int k, int v, int &x, int &y) {
	if (!k) {
		x = y = 0;
		return;
	}
	pushdown(k);
	if (t[k].val <= k) {
		int x=newcode();  //
		r[x] = r[k];  //
		split(t[x].r, v, t[x].r, y);
		pushup(x);
	} else {
		int y=newcode();  //
		r[y] = r[k];  //
		split(t[k].l, v, x, t[k].l);
		pushup(y);
	}
}

可以看到，这里的 split 直接在修改的当前点新开了一个点来保存修改后的情况。而 merge 也是同理：

int merge(int x, int y) {
    if (!x || !y) return x + y;
    if (t[x].rnd < t[y].rnd) {
		int k=newcode();  //
		r[k] = r[x];  //
        t[k].r = merge(t[k].r, y);
        pushup(k);
        return k;
    } else {
		int k=newcode();  //
		r[k] = r[y];  //
        t[k].l = merge(x, t[k].l);
        pushup(k);
        return k;
    }
}

最后，merge 操作会返回一个新的根，这个根就是当前版本的根。然后可持久化部分就搞定了~

还有一部分区间操作的操作，以及例题的讲解，咕了。

posted @ 2024-12-27 16:59 ayaka0928 阅读(205) 评论(2) 收藏举报

刷新页面返回顶部

ayaka的博客

学无止境呢。