各种反演难题训练集合
1.loj[6181]某个套路求和题
题意:
从前有个 alpha1022,他在看某本奇妙的书的时候想到了这样一个函数:
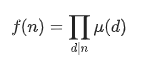
然后就有了这样一个问题:

解体思路:
观察发现,$f(i)$的值只有3种:0,-1,1。所以我们可以枚举不同值的方案数来得到答案。
首先考虑最好想的情况:值为0。易证当仅当一个数i有平方因子时才会为0.
然后对于一个数n,考虑(-1)的指数。假设i的质因子个数为m。指数根据组合数知识可以得到:$\sum_{i=0}^{m}i\binom{m}{i}$
对于上面的式子,当i取值k和m-k的时候组合数的值相同,所以合并一下可以得到:$\frac{1}{2}\sum_{i=0}^{m}m\binom{m}{i}$
根据二项式定理可以得到:指数为$m2^{m-1}$。
分析发现只有m为1时,也就是说只有n为质数的时候$f(i)$值才是-1,其余情况都是1。
于是可以考虑算出无平方因子的数的个数,然后减去质数的贡献。
注意是质数的贡献而不是质数的个数的原因是我们一开始算全部答案的时候默认i为质数时答案为1,而实际上答案是-1,差为2,所以贡献是质数的个数*2。
至于质数的贡献显然与质数的个数有关,因此min25筛可以解决后半部分。
对于无平方因子的数的个数,根据莫比乌斯函数的定义,我们知道答案就是$\sum_{i=1}^{n}\mu ^2(i)$。
直接算复杂度不对,我们考虑狄利克雷卷积或者莫比乌斯反演。
设$g(x)$表示x的最大平方因子的值。
显然$\sum_{i=1}^{n}\mu ^2(i)=\sum_{i=1}^{n}[g(i)=1]$
由于狄利克雷卷积中$Id∗1=σ1$
所以$\sum_{i=1}^{n}[g(i)=1]=\sum_{i=1}^{n}\sum_{k|g(i)}\mu (k)$
$=\sum_{d=1}^{n}\mu (d)\sum_{k|g(i)}$
$=\sum_{d=1}^{n}\mu (d)\sum_{k^2|i}$
$=\sum_{d=1}^{n}\mu (d)\frac{n}{d^2}$
至于这个东西我们发现n大于$\sqrt n$的时候对答案不会有任何贡献,因此枚举范围最大到$\sqrt n$即可。
这道题我们就愉快的AC啦~。
#include <bits/stdc++.h> #define inc(i,a,b) for(register int i=a;i<=b;i++) using namespace std; int miu[200010],vis[200010],prime[200010],num,sg[200010]; const int p=998244353; void pre(int n){ inc(i,1,n) miu[i]=1; inc(i,2,n){ if(vis[i]) continue; miu[i]=-1; for(int j=2*i;j<=n;j+=i){ vis[j]=i; if((j/i)%i==0) miu[j]=0; else miu[j]*=-1; } } inc(i,1,n) vis[i]=0; vis[1]=1; inc(i,1,n){ if(vis[i]==0){ prime[++num]=i; sg[num]=sg[num-1]+1; } for(register int j=1;j<=num&&prime[j]*i<=n;j++){ vis[i*prime[j]]=1; if(i%prime[j]==0)break; } } } long long n,sqrtn; long long ans=0,w[2000010],ind1[2000010],ind2[2000010],tot,g[2000010]; int main(){ cin>>n; sqrtn=sqrt(n); pre(sqrtn); for(long long i=1;i<=sqrtn;i++) ans=((ans+miu[i]*(n/(i*i))%p)+p)%p; for(long long i=1;i<=n;){ long long j=n/(n/i); w[++tot]=n/i; g[tot]=w[tot]-1; if(n/i<=sqrtn) ind1[n/i]=tot; else ind2[n/(n/i)]=tot; i=j+1; } inc(i,1,num){ //cout<<i<<endl; inc(j,1,tot){ if(1ll*prime[i]*prime[i]>w[j]) break; long long k=((w[j]/prime[i]<=sqrtn)?(ind1[w[j]/prime[i]]):(ind2[n/(w[j]/prime[i])])); g[j]-=g[k]-sg[i-1]; } } //cout<<"ac"; cout<<((ans-2*g[1])%p+p)%p<<endl; }
总结:对于$\sum_{i=1}^{n}\mu ^2(i)$我们可以考虑枚举最大平方因子。
2.loj[6244]七选五
题意:
首先我们可以注意到,无论标准答案p是什么都不会影响我们要求的东西,所以我们不妨假设p为{1,2,3,...,k}。也就是$p_i=i$
这时候我们会发现,从k+1一直到n这(n-k)个数无论放在什么位置对和的贡献都是0,所以我们考虑设函数$f(x)$表示从1到x+(n-k)个数中有序的选取x个数,且选出的序列是一个错排的方案数。
这里简单说一下错排在这里的定义:不存在一个i使得$i=p_i$。
显然的,答案就是$C_k^xf(k-x)$ 意义就是考虑哪x位与$p_i$相同,剩下的k-x+n-k个数错排的方案数就是刚才我们定义函数的意义。
因为$f(x)$不好直接求出来,所以我们考虑二项式反演。
我们设$g(x)$表示从1到x+(n-k)个数中有序的选取x个数的方案数。
显然的,根据排列数定义我们得到:$g(x)=P_{x+n-k}^{x}$
考虑$f()$和$g()$的意义上的关系,我们得到:$g(x)=\sum_{i=0}^{x}C_x^{i}f(i)$,意义就是枚举有哪几个位置相同,然后乘上其它位不变但把这几位换成错排的方案数。
最后根据二项式反演定理之二:$g(x)=\sum_{i=0}^{x}C_x^if(i)\Leftrightarrow f(x)=\sum_{i=0}^{x}(-1)^{x-i}C_x^ig(i)$
提前预处理出$g(i)$,我们就可以做到$O(n)$的求出f(k-x)。
这道题就轻松AC了。
#include <bits/stdc++.h> #define inc(i,a,b) for(register int i=a;i<=b;i++) const int p=1e9+7; using namespace std; long long KSM(long long a,long long b){ long long res=1; while(b){ if(b&1) res=res*a%p; a=a*a%p; b/=2; } return res; } long long n,k,x,fac[1000010]; long long P(long long n,long long m){ if(!m) return 1; if(m>n) return 0; return fac[n]*KSM(fac[n-m],p-2)%p; } long long g[1000010]; long long C(long long n,long long m){ if(!m) return 1; if(m>n) return 0; return fac[n]*KSM(fac[m],p-2)%p*KSM(fac[n-m],p-2)%p; } int main(){ cin>>n>>k>>x; fac[0]=1; inc(i,1,1000000) fac[i]=fac[i-1]*i%p; inc(i,0,k-x) g[i]=P(i+n-k,i)%p; long long ans=0; inc(i,0,k-x){ long long tmp=(k-x-i)%2; if(tmp!=0) tmp=-1; else tmp=1; ans=((ans+C(k-x,i)*tmp%p*g[i]%p)%p+p)%p; } ans=ans*C(k,x)%p; cout<<ans; }
总结:遇到不会算的组合数,我们可以考虑二项式反演。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号