快速数论变换(NTT)

说讲解NTT之前，我们先说简单一下FFT和卷积。

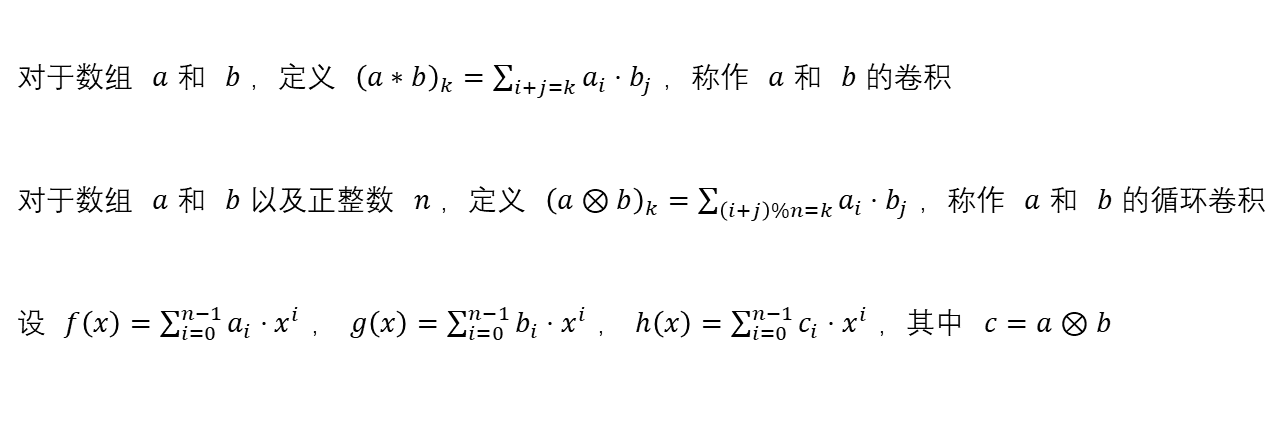
由此可见，我们的FFT最大的用处便是处理卷积问题。比如说CF993E

但在如今的OI界，取模之风逐渐替代了高精之风。我们使用已经过时的double其实并不是什么明智之举。有什么解决它的好办法呢？

有倒是有，但是需要提前学习原根这一概念。

原根：

虽然只看定义会感觉很迷惑，但有一点很明显:并不是所有的数都有原根。具体的：只有2,4,$p^k$,$2p^k$有原根，其中p是除了2以外的任意质数。k是任意正整数。

光有定义什么都做不到，我们需要前人推出来的性质。

性质1：如果g是n的原根，那么$g^0,g^1,...,g^{\phi(n)-1}$在模n的意义下均不同。

性质2：对于互质的正整数 𝑔,𝑛 ，设$ 𝑝_1,𝑝_2,⋯,𝑝_𝑘 $为 𝜑(𝑛) 的所有质因数，若 𝑔 是 𝑛 的原根，则对于 ∀𝑖∈[1,𝑘] ，有$g^{\frac{𝜑(𝑛)}{𝑝_𝑖}}\not\equiv 1(mod$ $n)$

由性质2可以得到：对于一个正整数，如果它有原根，那么它最小的一个原根通常很小，所以我们可以从小到大枚举正整数，然后用上个性质检验。、

 

 

 

快速数论变换NTT:

 NTT 和 DFT 最大的差别就在于主单位根的选取，根据原根的性质，如果 𝑝 为质数，那么在 $𝔽_𝑝 $上$ 𝑔^{(𝑝−1)/𝑛}$就是 𝑛 次主单位根。

 

 

 

能被写成 $𝑡⋅2^𝑘+1$形式的质数也被叫作 NTT 模数，常见的 NTT 模数有：469762049、998244353、1004535809

 

现在我们会在 𝑝 为 NTT 模数的时候，做 𝔽_𝑝 上的 NTT 了，那么如果模数不是 NTT 模数该怎么办呢？

 

 

假设 𝑝 不是 NTT 模数，设 𝑎𝑛𝑠=𝑎∗𝑏 ，我们要求 𝑎𝑛𝑠%𝑝 ，那么我们可以取互不相同的 NTT 模数 𝑞_1,𝑞_2,⋯,𝑞_𝑘 ，通过 NTT 求出 𝑎𝑛𝑠%𝑞_1,𝑎𝑛𝑠%𝑞_2,⋯𝑎𝑛𝑠%𝑞_𝑘 ，然后用中国剩余定理求出 𝑎𝑛𝑠%𝑝

 

 

至于要取几个 NTT 模数，只要保证 ∏_(𝑖=0)^𝑘▒𝑝_𝑖  大于 𝑎∗𝑏 数组里的最大值即可。一般情况下取 469762049、998244353、1004535809 就足够了，所以这种方法也被称为三模 NTT

 

 

#include <bits/stdc++.h>
#define inc(i,a,b) for(register int i=a;i<=b;i++)
using namespace std;
int n,m;
long long a[4000010],b[4000010];
const int p=998244353;
long long KSM(long long a,long long b){
    long long res=1;
    while(b){
        if(b&1) res=res*a%p;
        a=a*a%p;
        b/=2;
    }
    return res;
}
int rev[4000010],num,limit=1;
void NTT(long long *now,int type){
    inc(i,0,limit-1) if(i<rev[i]) swap(now[i],now[rev[i]]);
    for(int mid=1;mid<limit;mid<<=1){
        long long g=KSM(3,(p-1)/(mid<<1))%p;
        if(type==-1) g=KSM(g,p-2)%p;
        for(int l=0,r=(mid<<1);l<limit;l+=r){            
            for(long long w=1,j=0;j<mid;j++,w=w*g%p){
                long long x=now[l+j],y=w*now[l+j+mid]%p;
                now[l+j]=(x+y)%p;
                now[l+j+mid]=(x-y+p)%p;
            }
        }
    }
}
int main(){
    cin>>n>>m;
    inc(i,0,n) scanf("%lld",&a[i]);
    inc(i,0,m) scanf("%lld",&b[i]);
    while(limit<=(n+m)) limit<<=1,num++;
    inc(i,0,limit-1) rev[i]=((rev[i>>1]>>1)|((i&1)<<(num-1))); 
    //cout<<11111;
    NTT(a,1); NTT(b,1);
    inc(i,0,limit-1) a[i]=(a[i]*b[i])%p;
    NTT(a,-1);
    long long inv=KSM(limit,p-2);
    inc(i,0,n+m) printf("%lld ",a[i]*inv%p);
}