后缀自动机

简介

后缀自动机，是一个能够解决许多字符串相关问题的，十分强力的数据结构。
不要被博客的链接迷惑了，后缀自动机是 Suffix Automaton 。

后缀自动机可以存储下一个字符串的所有子串，并且做到线性时空复杂度。
准确来说，对于一个长度为 $n$ 的字符串构造后缀自动机，其中至多有 $2n-1$ 个节点与 $3n-4$ 条转移边。

定义

后缀自动机是一个DFA（确定性有限自动机或确定性有限状态自动机）。它接受且只接受 $s$ 的所有子串。

展开来说的话，可以概括成这么几点：

1. 后缀自动机是一个有向无环图。其中的节点叫做状态，边叫做转移。
2. 图中包含一个初始节点 $t_0$ ，任何节点都可以由之经过一系列的转移到达。
3. 每一个转移都标有一个字母，且从某一个节点出发的每一个转移都是不同的。
4. 自动机存在多个终止状态。如果我们从初始状态 $t_0$ 出发，最终转移到了一个终止状态，则路径上的所有转移连接起来一定是字符串 $s$ 的一个后缀。 $s$ 的每个后缀均可用一条从 $t_0$ 到某个终止状态的路径构成。
5. 在所有满足上述条件的自动机中，后缀自动机的结点数是最少的。

子串

一个字符串的后缀自动机包含关于这个字符串子串的所有信息。
更准确地来说，对于任意从初始节点 $t_0$ 开始的路径，我们将其转移边上的字符拿下来按顺序排列，都可以得到原字符串的一个子串。
这里需要注意：一条路径对应一个子串，但是一个子串不一定只对应一条路径。

性质

结束位置 endpos

对于字符串 $s$ 的一个子串 $t$ ，我们记其在字符串 $s$ 中的所有结束位置为 $\operatorname{endpos}(t)$ 。例如对于字符串 $aabbabd$ ，我们有 $\operatorname{endpos}(ab)=\{ 2,4 \}$。
两个子串 $t_1$ 与 $t_2$ 的endpos集合可能相等。这样，所有字符串 $s$
的非空子串都可以根据其endpos集合分为若干等价类。
而我们知道，后缀自动机中的每个状态对应一个或多个endpos相同的子串，即一个等价类。
这就很好地解释了上面所说的除了最小性之外的所有性质。

基于endpos，我们可以得到一系列重要结论：

引理1： 字符串 $s$ 的两个非空子串 $u$ 和 $v$ （假设 $|u| \leq |v|$ ）的endpos相同，当且仅当字符串 $u$ 在 $s$ 中的每次出现，都是以 $v$ 后缀的形式存在的。

证明：自己画图看看。既然 $u$ 与 $v$ 的endpos已经相同了，那么说明两者拥有相同的后缀（不理解就画图！）。而当 $|u| \leq |v|$ 时， $u$ 显然为 $v$ 的一个后缀。

引理2： 考虑两个非空子串 $u$ 与 $v$ （仍然假设 $|u| \leq |v|$ ）。两者的endpos满足这样的一个关系：

$$\begin{cases} \operatorname{endpos}(v) \subseteq \operatorname{endpos}(u) & \text{if } u \text{ is a suffix of } v\\\\ \operatorname{endpos}(v) \cap \operatorname{endpos}(u) = \varnothing & \text{otherwise} \end{cases}$$

证明：如果 $\operatorname{endpos}(u) \cap \operatorname{endpos}(v) \neq \varnothing$ ，那么结合我们刚刚证明完的引理1，我们可以知道 $u$ 是 $v$ 的一个后缀。既然 $u$ 是 $v$ 的一个后缀了，那么对于所有 $v$ 出现的地方， $u$ 也会出现，即 $\operatorname{endpos}(u) \subseteq \operatorname{endpos}(v)$ 。而如果 $u$ 的长度小于 $v$ 且 $u$ 还不是 $v$ 的后缀，那么 $v$ 出现的地方 $u$ 一定不会出现，即 $\operatorname{endpos}(u) \cap \operatorname{endpos}(v) = \varnothing$ 。

引理3: 对于任意一个endpos等价类（或者一个状态），其包含的所有子串都是最长子串的连续后缀。

证明：我们考虑等价类中两个子串：最长的，记为 $u$ ；最短的，记为 $v$ 。如果 $u=v$ 那么显然不用证明。如果不是，那么对于长度在区间 $\[ |u| , |v| \]$ 内的子串。根据引理1，在这个等价类中，必定存在子串有 $v$ 为后缀且同时为 $u$ 的后缀。

后缀链接 link

根据引理3，我们可以知道对于任意状态，其中包含的字串都是其中最长子串的一段连续后缀。这段连续后缀不一定可以覆盖 $\[ 1,|\text{最长子串}| \]$ 这一整个区间，但一定是连续的。
我们可以将其看做是不断将最长子串的首个字符删去得到子串的一个过程。

而当我们不断删去，直到删去最短子串的首个字符的时候，我们会发现我们已经离开了这个状态。
我们可以根据这样一个走向创建一系列的新边。
这些新边就被称为link边，也叫做后缀链接。
有些地方也叫fa/father边。

引理4： 所有后缀链接构成一棵根节点为 $t_0$ 的树。

证明：根据后缀链接的定义及引理3，我们可以看出，当前状态的后缀链接到达的是严格更短的字符串。而沿着后缀链接走，最后总能到达代表着空字符串的 $t_0$ 。

我们将后缀链接与endpos关联一下。
根据引理2，我们可以得出，两个endpos等价类不是互相包含，就是互不相交。根据这个包含关系，我们可以列出一棵endpos等价类的树。
对应在后缀自动机上就是对状态建树。

引理5： 通过 $\operatorname{endpos}$ 集合构造的树（每个子节点的子集都包含在父节点的子集中）与通过后缀链接构造的树相同。

证明：是树的证明上面有了，我们看一下对于两者相同的证明。
考虑任意非 $t_0$ 的状态 $u$ 及其后缀链接 $\operatorname{link}(u)$ 。根据引理2和后缀链接的定义，我们可以知道 $\operatorname{endpos}(u) \varsubsetneqq \operatorname{endpos}(\operatorname{link}(u))$ 。这样，我们在建树的时候，就会在 $u$ 与 $\operatorname{link}(u)$ 之间连一条边。

构建

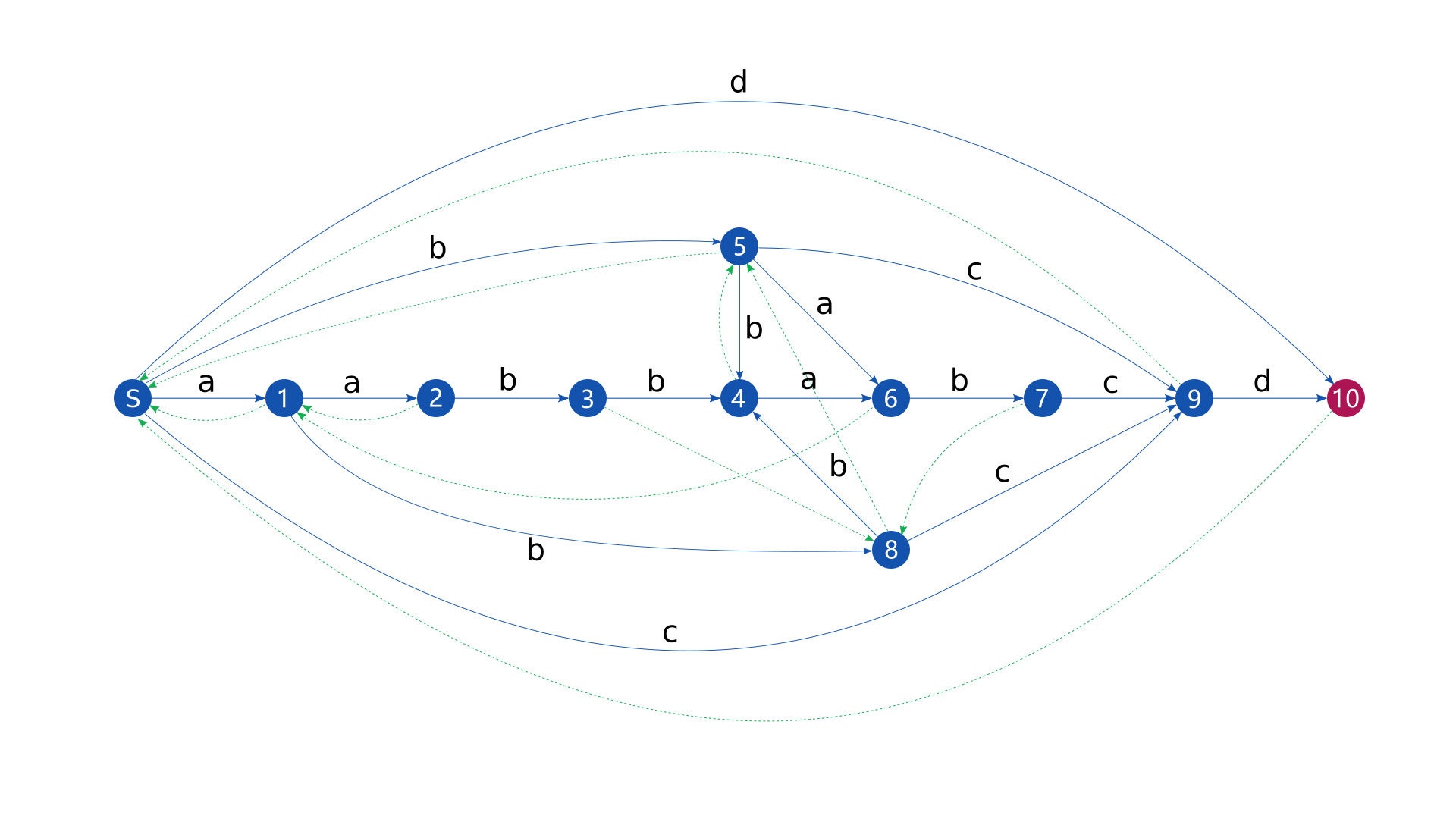
下面是对字符串 $aabbabcd$ 构建后缀自动机得到的结果。
其中，蓝色(#1453AD)的边代表的是转移，绿色(#14AD53)的边代表的是后缀链接。
蓝色(#1453AD)的点代表状态，紫色(#AD1453)的点代表终止状态。

算法

构建后缀自动机的算法是个在线算法。我们逐个加入字符串中的每个字符，并在每一步中相应地维护刚刚得到的后缀自动机。
为了保证线性的空间复杂度，我们只保存len与link的值。终止状态的值可以在构建完自动机之后求出。

在最开始，整个后缀自动机只会包含一个节点： $t_0$ ，编号为0。我们指定len[0] = 0，link[0] = -1。这里的$-1$表示的是一个虚拟的状态。
然后我们就可以向后缀自动机内添加字符了。

我们向后缀自动机内添加一个字符 $c$ 的算法流程如下：

我们令last为先前对应整个字符串的状态（一开始我们设last = 0）。

创建一个新的状态cur，并使len[cur] = len[last] + 1。

从状态last开始，不断遍历后缀链接。
如果还没有到字符 $c$ 的转移，我们就添加一个指向cur的转移。
如果在某个点已经存在到字符 $c$ 的转移，我们就停下来，并将这个状态记为p。
如果没有找到这样的状态p，我们最终会到达虚拟状态$-1$，这时我们使link[cur] = 0并退出。

如果我们找到了一个状态p，其可以通过字符 $c$ 转移，我们将这样转移到的状态标记为q。
现在我们考虑我们找到的q是否满足len[p] + 1 = len[q]这个条件。

如果满足，那么我们就只需要使link[cur] = q并退出。

如果不满足，那么情况就会变得复杂。
我们需要复制一个状态q，标记为nq。nq将会获得q除了len以外的所有信息。我们将len[nq]赋值为len[p] + 1。之后，我们使link[cur] = link[q] = nq。
之后，使用后缀链接从p往回走，并把沿途所有指向q的转移重定向至nq。

最后，我们将last的值更新为cur。

寻找终止状态

如果我们还想要知道哪些状态是终止状态而那些不是，我们可以在构建完 $s$ 对应的后缀自动机之后再进行寻找。

我们从刚才最后一步得到的last处开始遍历后缀链接，直到最终到达初始节点。
我们将沿途的所有状态都标记为终止状态，因为他们存储着原字符串 $s$ 的至少一个后缀。

证明

这里我们引用一下OI-Wiki上的证明。

{% note 正确性证明 %}

• 若一个转移 $(p,q)$ 满足len[p] + 1 =len[q]，则我们称这个转移是 连续的。否则，即当len[p] + 1 < len[q]时，这个转移被称为 不连续的。从算法描述中可以看出，连续的、不连续的转移是算法的不同情况。连续的转移是固定的，我们不会再改变了。与此相反，当向字符串中插入一个新的字符时，不连续的转移可能会改变（转移边的端点可能会改变）。
• 为了避免引起歧义，我们记向后缀自动机中插入当前字符 $c$ 之前的字符串为 $s$。
• 算法从创建一个新状态cur开始，对应于整个字符串 $s+c$。我们创建一个新的节点的原因很清楚。与此同时我们也创建了一个新的字符和一个新的等价类。
• 在创建一个新的状态之后，我们会从对应整个字符串 $s$ 的状态通过后缀链接进行遍历。对于每一个状态，我们尝试添加一个通过字符 $c$ 到新状态cur的转移。然而我们只能添加与原有转移不冲突的转移。因此我们只要找到已存在的 $c$ 的转移，我们就必须停止。
• 最简单的情况是我们到达了虚拟状态 $-1$，这意味着我们为所有 $s$ 的后缀添加了 $c$ 的转移。这也意味着，字符 $c$ 从未在字符串 $s$ 中出现过。因此cur的后缀链接为状态 $0$。
• 第二种情况下，我们找到了现有的转移 $(p,q)$。这意味着我们尝试向自动机内添加一个 已经存在的 字符串 $x+c$（其中 $x$ 为 $s$ 的一个后缀，且字符串 $x+c$ 已经作为 $s$ 的一个子串出现过了）。因为我们假设字符串 $s$ 的自动机的构造是正确的，我们不应该在这里添加一个新的转移。然而，难点在于，从状态cur出发的后缀链接应该连接到哪个状态呢？我们要把后缀链接连到一个状态上，且其中最长的一个字符串恰好是 $x+c$，即这个状态的len应该是len[p] + 1。然而还不存在这样的状态，即len[q] > len[p] + 1。这种情况下，我们必须通过拆开状态q来创建一个这样的状态。
• 如果转移 $(p,q)$ 是连续的，那么len[q] = len[p] + 1。在这种情况下一切都很简单。我们只需要将cur的后缀链接指向状态q。
• 否则转移是不连续的，即len[q] > len[p] + 1，这意味着状态q 不只对应于长度为len[p] + 1的后缀 $s+c$，还对应于 $s$ 的更长的子串。除了将状态q拆成两个子状态以外我们别无他法，所以第一个子状态的长度就是len[p] + 1了。
  我们如何拆开一个状态呢？我们 复制 状态q，产生一个状态nq，我们将len[nq] 赋值为len[p] + 1。由于我们不想改变遍历到q的路径，我们将q的所有转移复制到nq。我们也将从nq出发的后缀链接设置为q的后缀链接的目标，并设置q的后缀链接为nq。
  在拆开状态后，我们将从cur出发的后缀链接设置为nq$。
  最后一步我们将一些到q转移重定向到nq。我们需要修改哪些转移呢？只重定向相当于所有字符串 $w+c$（其中 $w$ 是p的最长字符串）的后缀就够了。即，我们需要继续沿着后缀链接遍历，从结点p直到虚拟状态 $-1$ 或者是转移到不是状态q的一个转移。

{% note 操作次数线性证明 %}
首先我们假设字符集大小为 常数。如果字符集大小不是常数，SAM 的时间复杂度就不是线性的。从一个结点出发的转移存储在支持快速查询和插入的平衡树中。因此如果我们记 $\Sigma$ 为字符集，$\left|\Sigma\right|$ 为字符集大小，则算法的渐进时间复杂度为 $O(n\log\left|\Sigma\right|)$，空间复杂度为 $O(n)$。然而如果字符集足够小，可以不写平衡树，以空间换时间将每个结点的转移存储为长度为 $\left|\Sigma\right|$ 的数组（用于快速查询）和链表（用于快速遍历所有可用关键字）。这样算法的时间复杂度为 $O(n)$，空间复杂度为 $O(n\left|\Sigma\right|)$。

所以我们将认为字符集的大小为常数，即每次对一个字符搜索转移、添加转移、查找下一个转移。这些操作的时间复杂度都为 $O(1)$。

如果我们考虑算法的各个部分，算法中有三处时间复杂度不明显是线性的：

• 第一处是遍历所有状态last的后缀链接，添加字符 $c$ 的转移。
• 第二处是当状态q被复制到一个新的状态nq时复制转移的过程。
• 第三处是修改指向q的转移，将它们重定向到nq的过程。

我们使用后缀自动机的大小（状态数和转移数）为 线性的 的事实（对状态数是线性的的证明就是算法本身，对转移数为线性的的证明将在稍后实现算法后给出）。

因此上述 第一处和第二处 的总复杂度显然为线性的，因为单次操作均摊只为自动机添加了一个新转移。

还需为 第三处 估计总复杂度，我们将最初指向q的转移重定向到nq。我们记v = longest[p]，这是一个字符串 $s$ 的后缀，每次迭代长度都递减——因为字符串 $s$ 的位置每次迭代都单调上升。这种情况下，如果在循环的第一次迭代之前，相对应的字符串 $v$ 在距离last的深度为 $k$ $(k \ge 2)$ 的位置上（深度记为后缀链接的数量），那么在最后一次迭代后，字符串 $v+c$ 将会成为路径上第二个从cur出发的后缀链接（它将会成为新的last的值）。

因此，循环中的每次迭代都会使作为当前字符串的后缀的字符串longest[link[link[last]]]的位置单调递增。因此这个循环最多不会执行超过 $n$ 次迭代，这正是我们需要证明的。

代码

洛谷板子题代码如下：

#define _CRT_SECURE_NO_WARNINGS
#include<bits/stdc++.h>
using namespace std;
const int N = 2000010;
int tot = 1, last = 1;
struct Node
{
	int len, fa;
	int s[26];
}node[N];
char str[N];
long long f[N];
long long ans;
int h[N], e[N], ne[N], idx;
void extend(int c)
{
	int p = last, np = last = ++tot;
	f[tot] = 1;
	node[np].len = node[p].len + 1;
	for(; (p) && (!node[p].s[c]); p = node[p].fa)node[p].s[c] = np;
	if(!p)
	{
		node[np].fa = 1;
	}
	else
	{
		int q = node[p].s[c];
		if(node[q].len == node[p].len + 1)
		{
			node[np].fa = q;
		}
		else
		{
			int nq = ++tot;
			node[nq] = node[q];
			node[nq].len = node[p].len + 1;
			node[q].fa = node[np].fa = nq;
			for(; (p) && (node[p].s[c] == q); p = node[p].fa)node[p].s[c] = nq;
		}
	}
	return;
}
void add(int a, int b)
{
	e[idx] = b, ne[idx] = h[a], h[a] = idx++;
	return;
}
void dfs(int u)
{
	for(int i = h[u]; ~i; i = ne[i])
	{
		dfs(e[i]);
		f[u] += f[e[i]];
	}
	if(f[u] > 1)ans = max(ans, f[u] * node[u].len);
	return;
}
int main()
{
	scanf("%s", str);
	for(int i = 0; str[i]; i++)extend(str[i] - 'a');
	memset(h, -1, sizeof(h));
	for(int i = 2; i <= tot; i++)add(node[i].fa, i);
	dfs(1);
	printf("%lld\n", ans);
	return 0;
}

应用

检查字符串是否出现

给定一个字符串 $S$ 和多个模式串 $P$ ，我们需要检查模式串 $P$ 是否作为 $S$ 的一个子串出现过。

我们首先给字符串 $S$ 构建后缀自动机。构建完了之后，我们从初始节点 $t_0$ 开始，不断向遍历trie树一样遍历后缀自动机。由于字符串 $S$ 内的每个字串都是其某个后缀的前缀，所以我们仅从初始节点开始遍历即可。
如果遍历完整个自动机都没有完全匹配，那么就说明模式串没有在原字符串里面出现过，反之亦然。

如果我们在这样历的同时记录下最大匹配长度，那么还可以得到模式串在字符串内匹配的最大前缀长度。

求不同子串个数

给定一个字符串 $S$ ，计算其不同子串的个数。

对其构造后缀自动机。
字符串 $S$ 中的每一个子串都相当于是自动机中的一些路径。因此不同字串的个数就等于自动几种以 $t_0$ 为起点的不同路径的条数。
考虑到后缀自动机是一个有向无环图，不同路径的条数可以通过动态规划来计算。
OIwiki上给的方法是这样的：

令 $d_v$ 为从状态 $v$ 开始的路径数量（包括长度为零的路径），则我们有如下递推方程：

$$d_v = 1 + \sum_{w:(v,w,c)\in DAWG} d_w$$

即， $d_v$ 可以表示为所有 $v$ 的转移的末端的和。
所以不同字串的个数为 $d_{t_0}-1$ （因为需要去掉空字串）

我个人更喜欢另一种方法：
利用后缀自动机的树形结构，每个节点对应的子串数量就是len[i] - len[link[i]]，对自动机所有节点求和即可。
这个在洛谷上有例题：Luogu P3804

其他的应用可以见OIwiki。

__EOF__

本文作者：Kaiser Wilheim
本文链接：https://www.cnblogs.com/kaiserwilheim/p/16005436.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！