bzoj2120 / P1903 [国家集训队]数颜色 / 维护队列(带修改莫队)
带修改的莫队
在原有指针$(l,r)$上又添加了时间指针$t$
贴一段dalao的解释
带修改的莫队,和原版莫队相比,多了一个时间轴
原版莫队是将区间(l,r)视为点(l,r),带修改的即加一维时间轴(l,r,t)
对于t轴的移动可以保存每次修改,如果修改在(l,r)间则更新
分块方法可以参照原版莫队,先将l分块,再讲r分块,同一块的按t排序
块大小为
可以达到最快的理论复杂度
,证明如下
设分块大小为a,莫队算法时间复杂度主要为t轴移动,同r块l,r移动,l块间的r移动三部分
t轴移动的复杂度为
,同r块l,r移动复杂度为
,l块间的r移动复杂度为
三个函数max的最小值当a为
取得,为
给出一个并不严格的假证明
每次查询时:
$t$轴每次最多移动$t$次。而$l,r$指针在块上的组合共$n^{2}/a^{2}$种,故复杂度$O(n^{2}t/a^{2})$
$l$轴每次最多移动$2a$次,最多$n$次。复杂度$O(na)$
$r$轴每次最多移动的次数是一个递减的等差数列:$n,n-a,n-2a.....$,最多共移动$((n+a)(n/a)/2)$次。所以复杂度就是$O(n^{2}/a)$辣
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cmath> using namespace std; void read(int &x){ static char c=getchar();x=0; while(c<'0'||c>'9') c=getchar(); while('0'<=c&&c<='9') x=x*10+(c^48),c=getchar(); } #define N 50005 struct data{int x,y,t,id;}a[N]; struct modi{int id,pre,now;}d[N]; int Len,n,m,Q,T,L,R,tot,b[N],c[1000005],ans[N]; inline int bel(int x){return (x-1)/Len+1;} bool cmp(data A,data B){ if(bel(A.x)!=bel(B.x)) return bel(A.x)<bel(B.x); if(bel(A.y)!=bel(B.y)) return bel(A.y)<bel(B.y); return A.t<B.t; } int main(){ char opt[3]; int q1,q2; read(n);read(m); register int i; for(i=1;i<=n;++i) read(b[i]); for(i=1;i<=m;++i){ scanf("%s",opt),read(q1),read(q2); if(opt[0]=='Q') a[++Q]=(data){q1,q2,T,Q}; else d[++T].pre=b[q1],d[T].id=q1,d[T].now=b[q1]=q2; } Len=ceil(exp((log(n)+log(T))/3));//bzoj酱紫写会RE,直接sqrt(n)就好辣 虽然复杂度没办法保证.... for(i=T;i;--i) b[d[i].id]=d[i].pre; sort(a+1,a+Q+1,cmp); L=R=1; T=0; c[b[1]]=tot=1; for(int i=1,Id;i<=Q;++i){ while(L<a[i].x) tot-=(c[b[L]]==1),--c[b[L]],++L; while(L>a[i].x) --L,tot+=(c[b[L]]==0),++c[b[L]]; while(R<a[i].y) ++R,tot+=(c[b[R]]==0),++c[b[R]]; while(R>a[i].y) tot-=(c[b[R]]==1),--c[b[R]],--R; while(T<a[i].t){ ++T; Id=d[T].id; if(L<=Id&&Id<=R) tot-=(c[b[Id]]==1),--c[b[Id]]; b[Id]=d[T].now; if(L<=Id&&Id<=R) tot+=(c[b[Id]]==0),++c[b[Id]]; } while(T>a[i].t){ Id=d[T].id; if(L<=Id&&Id<=R) tot-=(c[b[Id]]==1),--c[b[Id]]; b[Id]=d[T].pre; --T; if(L<=Id&&Id<=R) tot+=(c[b[Id]]==0),++c[b[Id]]; } ans[a[i].id]=tot; } for(i=1;i<=Q;++i) printf("%d\n",ans[i]); return 0; }
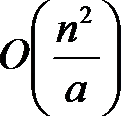

 浙公网安备 33010602011771号
浙公网安备 33010602011771号