转置卷积的操作介绍解读

本文大部分参考自> https://zhuanlan.zhihu.com/p/548904297 > 并进行了精简与修改，仅供学习使用。

一、卷积参数：

二维离散卷积：N=2；

输入大小：\(i_1=i_2=i\)；

卷积核大小：\(k_1=k_2=k\)；

两个方向的步长：\(s_1=s_2=s\)；

两个方向的padding数目：\(p_1=p_2=p\)；

二、卷积的操作方法：

卷积神经网络通过局部感受野捕捉输入数据（如图像）的边缘、纹理等低级特征，并逐层组合为高级特征（如物体形状）。‌

卷积的计算方法主要包括离散卷积的滑动窗口乘积求和（适用于图像处理）和连续卷积的积分运算，具体步骤涉及翻转、平移、乘积和求和/积分。

定义卷积核‌：选择一个大小为m \(\times\) n的矩阵（如3 \(\times\) 3的滤波器），称为卷积核或kernel。‌

‌滑动窗口操作‌：从输入矩阵左上角开始，将卷积核与对应位置的子矩阵逐元素相乘后求和，结果填入输出矩阵的对应位置。‌
公式： \(g(i,j)=\sum_{y=1}^n\sum_{x=1}^mf(x,y) \cdot h(x,y)\) ，
其中f为输入，h为卷积核。‌

边缘处理‌：若窗口超出输入矩阵边界，可采用补零、对称填充或忽略边缘像素。‌

例如对于图2.1，对于一个4 \(\times\) 4的输入图像，使用3 \(\times\) 3的卷积核进行卷积提取特征，则会得到一个2 \(\times\) 2的特征图输出。Padding表示额外填补图像边界的宽度，Stride表示滑动步长，实际对卷积核的作用请看2.4节的图4.5；

2.1 Padding=0，Stride=1

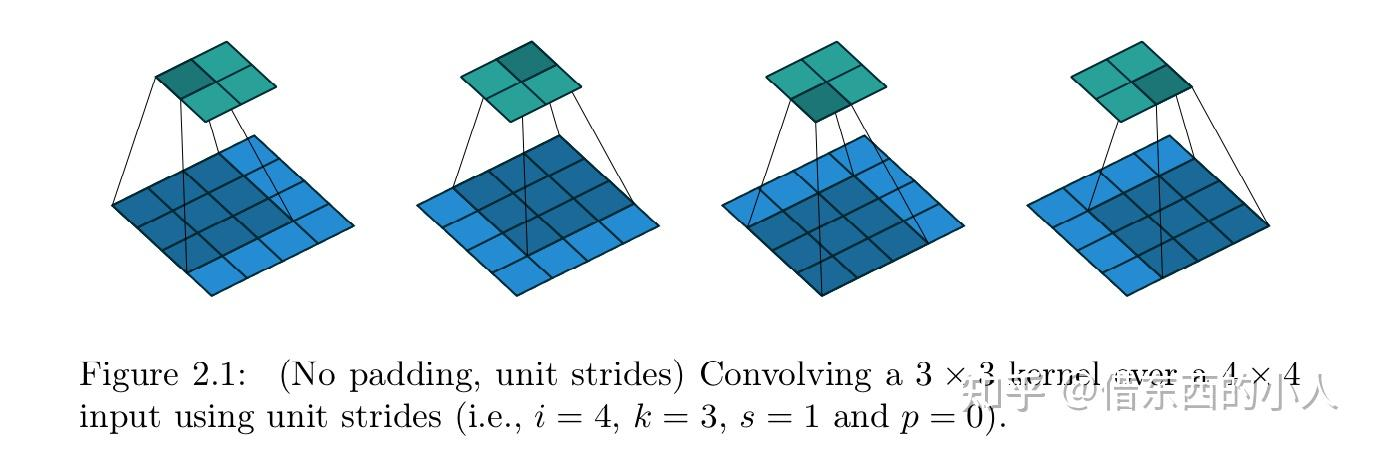
输出特征图大小：\(o=i-k+1\)

2.2 Padding=p，Stride=1

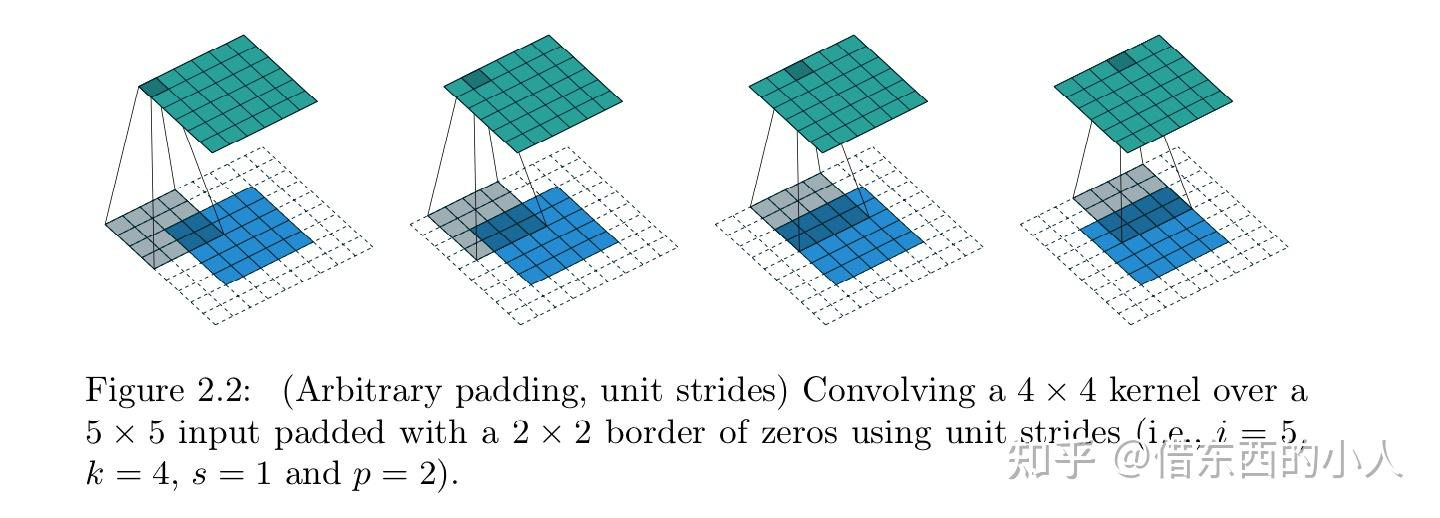
输出特征图大小：\(o=i-k+2p+1\)

特别的，half padding指 \(2p=k-1\) ，这样得到的输出与输入size一致。full padding指 \(p=k-1\) 。

2.3 Padding=0，Stride≠1

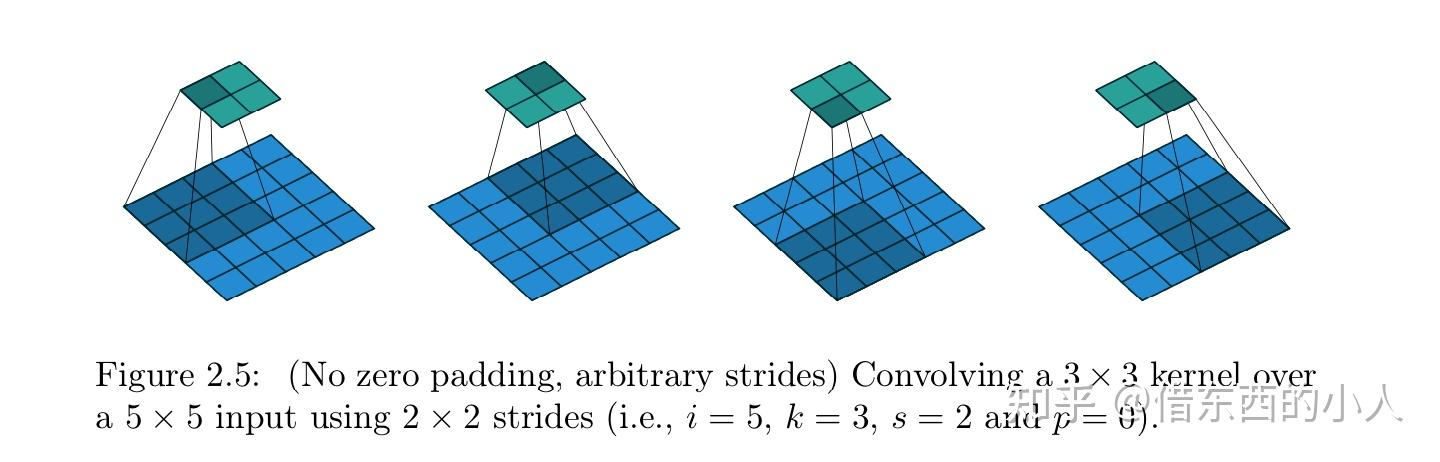
输出特征图大小：\(o=[\cfrac{i-k}{s}]+1\)

特别的，这也被称为池化运算。对输入特征图进行降维压缩的操作，其本质是采样。池化操作通过选择某种方式（如最大值或平均值）来压缩输入数据的空间维度，以加快神经网络的运算速度并减少计算量。最大池化通常用于突出前景和提取纹理信息，而平均池化则有助于保留背景信息。

2.4 转置卷积

常见的转置卷积有两种：
（1）一种是认为转置卷积是上采样的一种，其他几种上采样方法分别是最近邻插值、双线性插值和反池化，它们一起构成了上采样的方法；
（2）另一种理解是认为转置卷积和上采样属于并列关系，就像pytorch的调用方法一样，上采样和转置卷积的API不同，如下所示：

torch.nn.Upsample(size=None, scale_factor=None, mode='nearest', align_corners=None)

torch.nn.ConvTranspose1d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1, padding_mode='zeros')

转置卷积的操作方法：

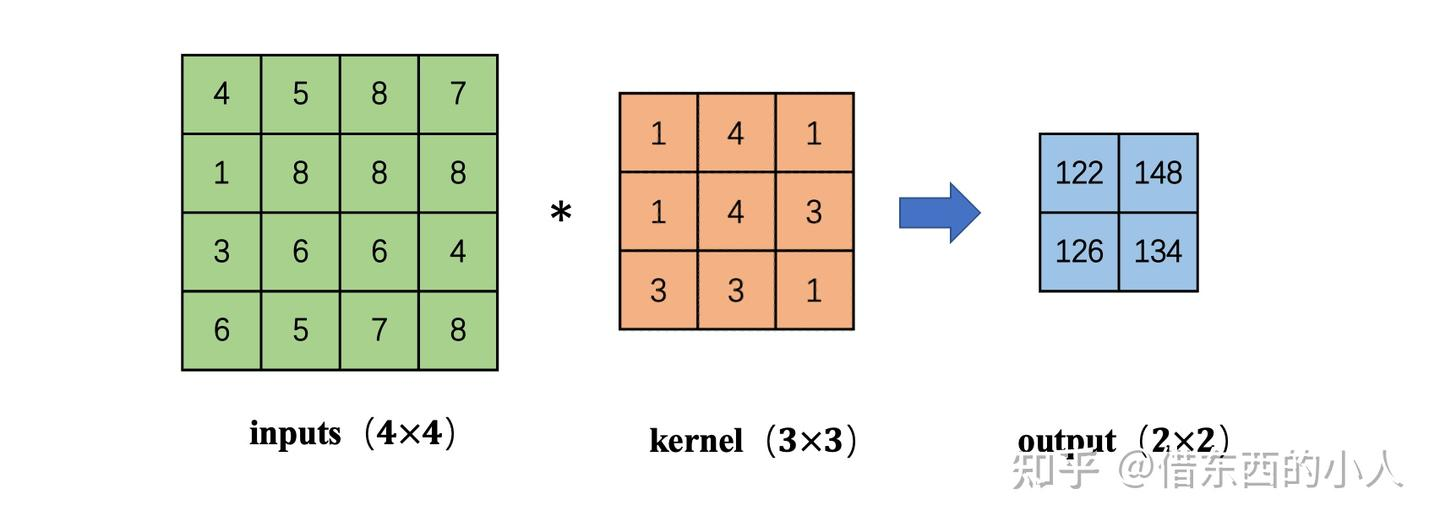
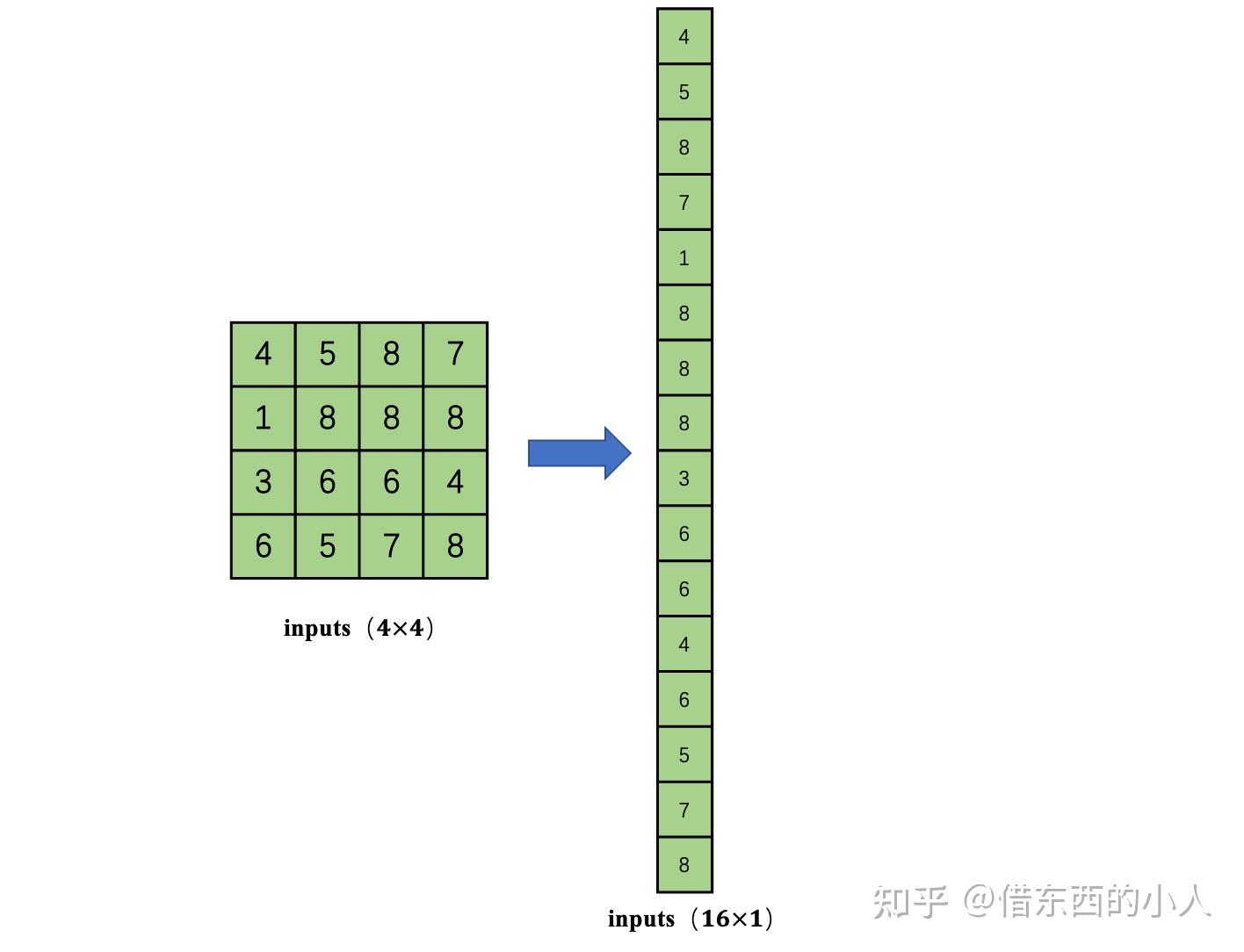
1.输入列展开

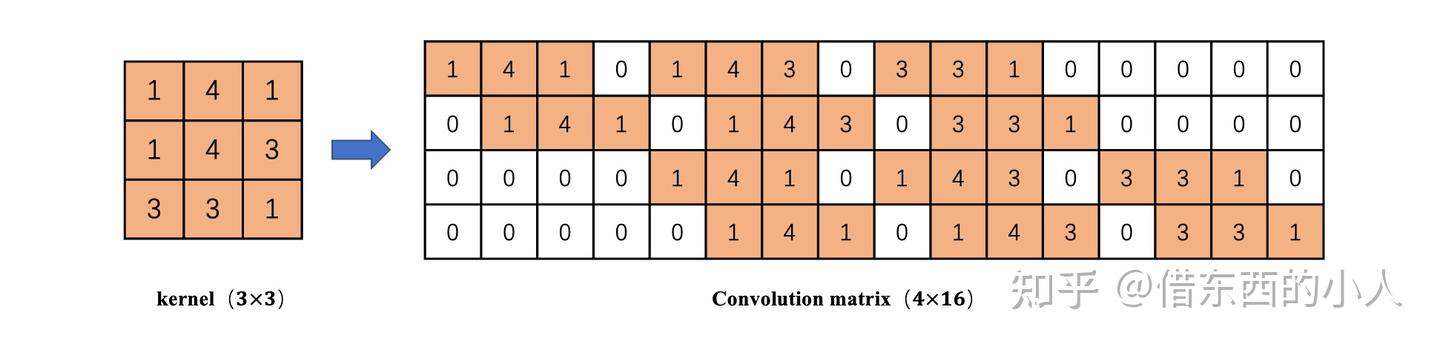
2.卷积核行展开

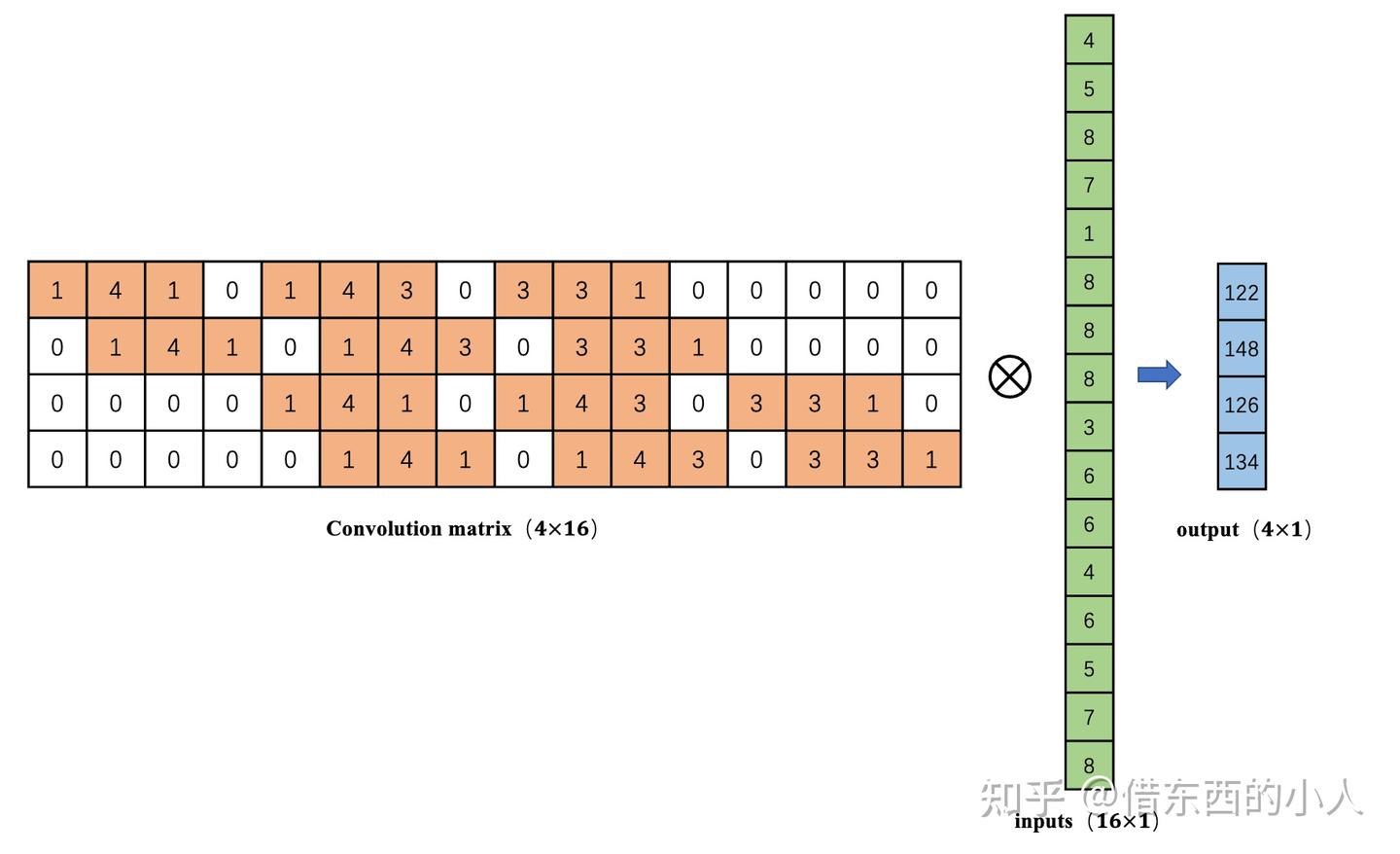
3.叉乘计算可以将16维压缩到4维

4.转置卷积的目的则在于，如何从4维倒推回16维的输入向量。

一个非常直观的做法是：对卷积矩阵求转置，再去计算矩阵相乘，这样就可以从输出特征图计算得到更高分辨率的输入特征图。

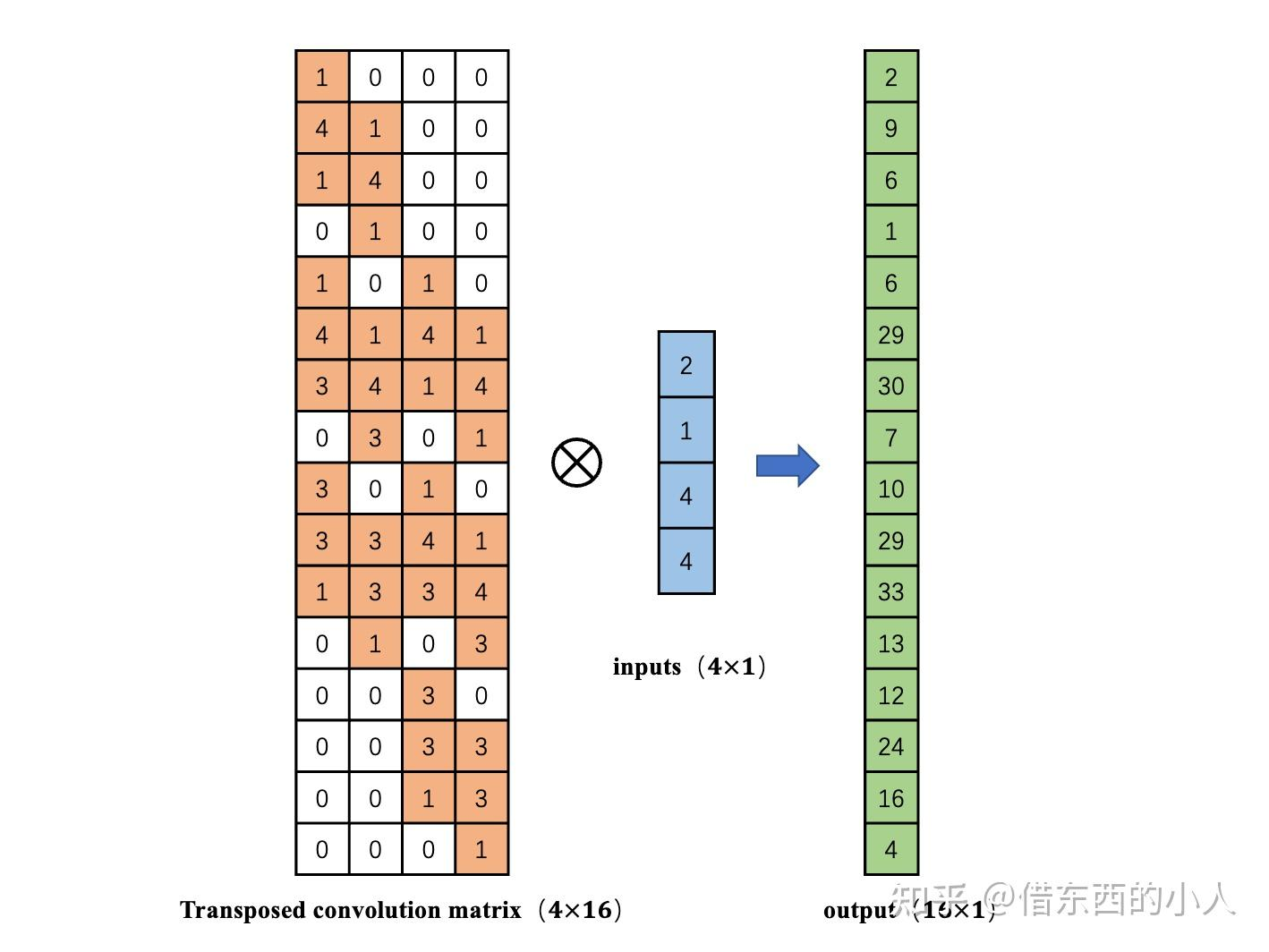
值得注意的是：

根据转置矩阵我们只能得到哪些位置的像素值应该是0，每个数值对应卷积核哪个位置的值，而这些数值要根据网络学习得到，而不是单纯的转置或逆；（补充：实际上）

这也是为什么有些人不赞同转置卷积被称为反卷积的原因；

转置卷积的计算方法：

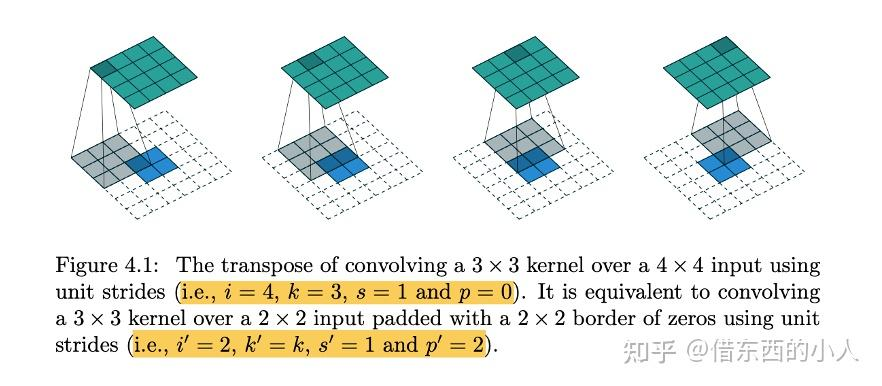
如图4.1，一个3 \(\times\) 3的卷积核作用在4 \(\times\) 4的输入图上得到2 $\time! 2的特征输出，就等价于3 $\time! 3的卷积核作用在padding=2的2 $\time! 2的输入图上得到4 \(\times\) 4 的输出特征。

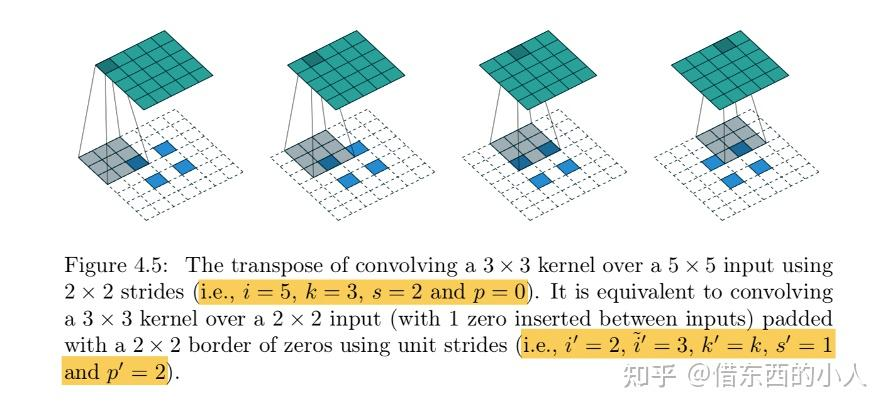
补充一个stride=2的案例

三、棋盘效应

我们在2.4小节介绍了一个比较特殊的卷积操作，转置卷积。该卷积核主要是用来实现上采样的算子操作，但该算子存在一定的缺陷，这就是本节要介绍的“棋盘效应”。

什么是棋盘效应？当在解码器中使用转置卷积作为上采样方法时，输出的feature map出现了如下图所示明显的网格状，这就有可能是转置卷积导致的“棋盘效应”：

这往往会导致这样的图片输出出现，不难看到有许多网格状的伪影：

Deconvolution and Checkerboard Artifacts > https://distill.pub/2016/deconv-checkerboard/ > 一文给出了解释，这是由不均匀重叠（uneven overlaps）导致的，当kernel size不能被stride整除时，我们容易看到如下图的不均匀重叠现象

拓展到二维上，这就演变成了棋盘效应。而且重要的是，在二维上这种增强重叠部分输出的情况由2倍会变为4倍。尽管卷积网络会通过调整权重来相消这种伪影，但实际情况中它们往往会使伪影叠加放大，从而在多种尺度上产生明显的视觉瑕疵。

另外有一种情况是，即使转置卷积已然被构建成了一种均匀覆盖的设计，

作者认为，转置卷积就是一种有问题的上采样方式：

·在最佳情况下，转置卷积是脆弱的：即使卷积核尺寸经过精心选择，它也非常容易表示出会产生伪影的函数。

·在最坏情况下，产生伪影就是转置卷积的默认行为。

在这里我们给出常见的两个解决办法：

1.确保反卷积的卷积核大小能被步长整除，这能大幅度缓解棋盘效应的出现（问题在于无法消除！）；

2.分离上采样与特征学习，先使用插值方法（如最近邻、双线性）将特征图放大，再用标准卷积层提取新空间尺度下的特征，训练更稳定（问题在于参数量增大，训练速度降低！）；

x = F.interpolate(x, scale_factor=2, mode='bilinear', align_corners=False)

x = nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1)(x)

特别地，pixelshuffle是方法1的一种等价的方法，即sub-pixel convolution> Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network >。简单来说，原文的主要思想在于将所有卷积都在低分辨率特征图上进行，最后通过一个特殊的层——Sub-Pixel Convolution——将通道信息重排到空间维度，实现上采样。该卷积方法的原理是先通过普通卷积扩展通道数（如放大 r² 倍），然后将通道维度上的值“搬”到空间维度上，实现分辨率放大。该方法在后续的超分方法上都有广泛使用。

点击查看代码

LR Input (H, W) 
    → Conv layers (在低分辨率上提取特征) 
    → 输出: (r² × C, H, W)   
    → Sub-Pixel Convolution (PixelShuffle)
    → 输出: (C, r×H, r×W)