Codeforces Round #315 (Div. 1) B. Symmetric and Transitive(Bell数的应用)(好题)
大致题意:
A set ρ of pairs (a, b) of
elements of some set A is called a binary relation on set A.
For two elements a and b of
the set A we say that they are in relation ρ,
if pair 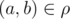 ,
in this case we use a notation
,
in this case we use a notation  .
.
Binary relation is equivalence relation, if:
-
It is reflexive (for any a it is true that
 );(自反律)
);(自反律) -
It is symmetric (for any a, b it
is true that if
 ,
then
,
then 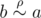 );
(交换律)
);
(交换律) -
It is transitive (if
 and
and 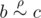 ,
than
,
than  ).(传递律)
).(传递律)

给出了等值Binary relation的定义,给定数的全集{1。2,3...,n}求有多少个ρ 集合满足等值关系中的2。3两条而不满足第一条
题意真是难理解...
思路:
仅仅要有某个元素a满足了2,3两条,就一定由  和
和 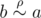 推出
推出 ,所以这个元素就满足了第一条
,所以这个元素就满足了第一条
同理假设这个集合中的每一个元素满足2,3条那么每一个元素都满足第一条也就是此集合成为了等值Binary relation。
所以为了不成为等值Binary relation,必须至少有一个元素x不满足全部关系。也就是不參与构成了某个二元组,除x外的元素恰好构成了等值Binary relation。
所以本题的答案就是 sigama(i:0,n-1){ C(n,i)*(这i元素构成的等值Binary relation的个数) }
如今问题变成i个元素能够构成多少个等值Binary relation
这个问题能够用递推解决,求dp[i],对于第i个元素必须满足这三个条件才行,所以必须让第i个元素与i-1个元素中的k个元素“混合”才行
比方{(a~b),(b~a),(a~a)}混入c后要满足等值Binary relation则变成{(a~b),(b~a),(b~c),(c~b),(a~c),(c~a),(a~a),(b~b),(c~c)}仅仅有唯一的混合结果
所以dp[i] = sigma(k:0,i-1){ C(i-1,k)*dp[i-1-k] } = sigma(k:0,i-1){ C(i-1,i-1-k)*dp[i-1-k] } = sigma(k:0,i-1){ C(i-1,k)*dp[k] }
会发现这就是Bell数的递推公式
所以求“i个元素能够构成多少个等值Binary relation”这个问题等价与“i的集合的划分方法的数目",比如:
集合{a, b, c}有5种不同的划分方法:
- {{a}, {b}, {c}}
- {{a}, {b, c}}
- {{b}, {a, c}}
- {{c}, {a, b}}
- {{a, b, c}};
每一个块中都是前面所说的混合构造成等值Binary relation,所以知道bell数的会非常easy解决此问题。到此问题已经圆满解决
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <iostream>
#include <cstring>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <string>
#include <vector>
#include <cstdio>
#include <ctime>
#include <bitset>
#include <algorithm>
#define SZ(x) ((int)(x).size())
#define ALL(v) (v).begin(), (v).end()
#define foreach(i, v) for (__typeof((v).begin()) i = (v).begin(); i != (v).end(); ++ i)
#define reveach(i, v) for (__typeof((v).rbegin()) i = (v).rbegin(); i != (v).rend(); ++ i)
#define REP(i,n) for ( int i=1; i<=int(n); i++ )
#define rep(i,n) for ( int i=0; i< int(n); i++ )
using namespace std;
typedef long long ll;
#define X first
#define Y second
typedef pair<int,int> pii;
template <class T>
inline bool RD(T &ret) {
char c; int sgn;
if (c = getchar(), c == EOF) return 0;
while (c != '-' && (c<'0' || c>'9')) c = getchar();
sgn = (c == '-') ? -1 : 1;
ret = (c == '-') ?
0 : (c - '0');
while (c = getchar(), c >= '0'&&c <= '9') ret = ret * 10 + (c - '0');
ret *= sgn;
return 1;
}
template <class T>
inline void PT(T x) {
if (x < 0) {
putchar('-');
x = -x;
}
if (x > 9) PT(x / 10);
putchar(x % 10 + '0');
}
const int N = 4000+123;
const int MOD = 1e9+7;
int bell[N][N];
int C[N][N];
int main(){
bell[0][0] = 1;
REP(i,N-10)
REP(j,i){
if(j == 1) bell[i][j] = bell[i-1][i-1];
else bell[i][j] = (bell[i][j-1]+bell[i-1][j-1])%MOD;
}
REP(i,N-10) {
C[i][i] = C[i][0] = 1;
REP(j,i-1) C[i][j] = (C[i-1][j-1]+C[i-1][j])%MOD;
}
int n;
while(~scanf("%d",&n)){
ll ans = 0;
rep(i,n) ans = (ans+C[n][i]*(ll)bell[i][i])%MOD;
PT(ans),puts("");
}
}
作为弱渣第一次遇过bell数,如今补充记录一些经常使用的基础知识:
Stirling数,第一类有点难理解不在此记录
第二类Stirling数是 个元素的划分成k个非空集合的方法数目。经常使用的表示方法有
个元素的划分成k个非空集合的方法数目。经常使用的表示方法有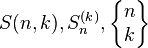 。
。
- 给定
 ,有递归关系
,有递归关系
证明递推式:考虑第n个物品。n能够单独构成一个非空集合,此时前n-1个物品构成k-1个非空的不可辨别的集合,有 种方法;也能够前n-1种物品构成k个非空的不可辨别的集合,第n个物品放入随意一个中。这样有
种方法;也能够前n-1种物品构成k个非空的不可辨别的集合,第n个物品放入随意一个中。这样有 种方法。
种方法。
Bell数:n的集合的划分方法的数目。
由定义能够得出它和第二类stirling数的关系: ,即划分成k个非空集合
,即划分成k个非空集合
有两个递推关系能够求bell数:
1.
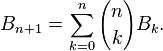
上述组合公式的证明:
能够这样来想,B_{n+1}是含有n+1个元素集合的划分的个数。考虑元素
如果他被单独划分到一类,那么还剩下n个元素。这样的情况下划分个数为 。
。
如果他和某一个元素被划分为一类,那么还剩下n-1个元素。这样的情况下划分个数为 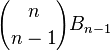 。
。
如果他和某两个元素被划分为一类,那么还剩下n-2个元素,这样的情况下划分个数为  ;
;
依次类推。得到了上述组合公式
2.依据贝尔三角形递推(较方便形象)
用下面方法建构一个三角矩阵(形式类似杨辉三角形):
- 第一行第一项是1(
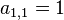 )
) - 对于n>1,第n行第一项等同第n-1行最后一项。
(
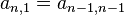 )
) - 对于m,n>1,第n行第m项等于它左边和左上方的两个数之和。(
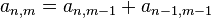 )
)
结果例如以下:(OEIS:A011971)
每行首项是贝尔数。
摘自:
https://zh.wikipedia.org/wiki/%E8%B4%9D%E5%B0%94%E6%95%B0
https://zh.wikipedia.org/wiki/%E6%96%AF%E7%89%B9%E7%81%B5%E6%95%B0



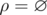 .
In other words, for a single element
.
In other words, for a single element 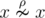 .
.

 浙公网安备 33010602011771号
浙公网安备 33010602011771号