深度学习梯度与反向传播

梯度与反向传播

1、梯度(方向向量)

1.1 什么是梯度

梯度：是一个向量，导数+变化最快的方向(学习的前进方向)

目标：通过梯度调整(学习)参数$w$,尽可能的降低$loss$

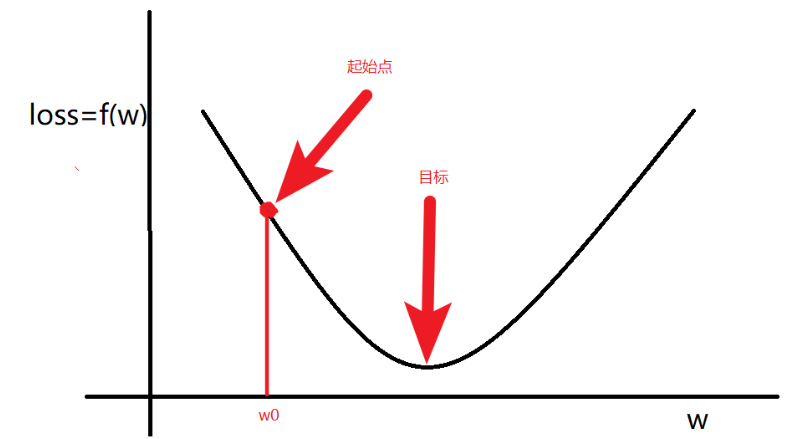
一般的，随机初始一个$w0$,通过优化器在学习率和梯度的调整下，让$loss$函数取到最小值。

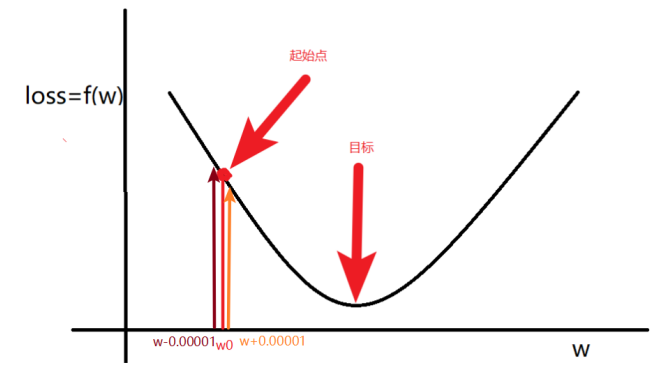
1.2 $w$的更新方法

1.计算$w$的梯度

\[\nabla w=\frac{f(w+0.000001)-f(w-0.000001)}{2*0.000001} \]

2.更新$w$

\[w=w-\alpha\nabla w \]

其中，$\nabla w < 0$意味着w将增大，$\nabla w > 0$意味着w将减小

总结：梯度就是多元函数参数的变化趋势（参数学习的方向），只有一个自变量时称为导数

1.3 偏导数与梯度计算

我们可以连结⼀个多元函数对其所有变量的偏导数，以得到该函数的梯度（gradient）向量。设函数为:

\[f:\mathbb{R}^n\to\mathbb{R}，\mathbf{x}=[x_1,x_2,\ldots,x_n]^\top \]

其输⼊是⼀个 $n$ 维向量 $x$，并且输出是一个标量。函数$f(x)$相对于$x$的梯度是⼀个包含$n$个偏导数的向量:

\[\nabla_{\mathbf{x}}f(\mathbf{x})=\left[\frac{\partial f(\mathbf{x})}{\partial x_1},\frac{\partial f(\mathbf{x})}{\partial x_2},\ldots,\frac{\partial f(\mathbf{x})}{\partial x_n}\right]^\top \]

假设$x$为$n$维向量，在微分多元函数时经常使⽤以下规则:

\[\bullet\text{ 对于所有}\mathbf{A}\in\mathbb{R}^{m\times n},\text{ 都有 }\nabla_{\mathbf{x}}\mathbf{A}\mathbf{x}=\mathbf{A}^\top \]

\[\bullet\text{ 对于所有}\mathbf{A}\in\mathbb{R}^{n\times m}\text{,都有 }\nabla_\mathbf{x}\mathbf{x}^\top\mathbf{A}=\mathbf{A} \]

\[\bullet\text{ 对于所有}\mathbf{A}\in\mathbb{R}^{n\times n}\text{,都有 }\nabla_\mathbf{x}\mathbf{x}^\top\mathbf{A}\mathbf{x}=(\mathbf{A}+\mathbf{A}^\top)\mathbf{x} \]

\[\bullet\nabla_{\mathbf{x}}\|\mathbf{x}\|^2=\nabla_{\mathbf{x}}\mathbf{x}^\top\mathbf{x}=2\mathbf{x} \]

公式证明：矩阵求导公式的数学推导（矩阵求导——基础篇） - 知乎 (zhihu.com)

1.4、链式法则

然而，上⾯⽅法可能很难找到梯度。这是因为在深度学习中，多元函数通常是复合（composite）的，所以我们可能没法应⽤上述任何规则来微分这些函数。幸运的是，链式法则使我们能够微分复合函数。让我们先考虑单变量函数。假设函数$ y = f(u)$ 和$ u = g(x)$ 都是可微的，根据链式法则：

\[\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}. \]

现在让我们把注意力转向一个更一般的场景, 即函数具有任意数量的变量的情况。假设可微分函数 $y$ 有变量$u_1,u_2,\ldots,u_m$,其中每个可微分函数$u_i$ 都有变量$x_1,x_2,\ldots,x_n$。注意, $y$是$x_1,x_2\mathbb{Q}\ldots,x_n$ 的函数。对于任意$i=1,2,\ldots,n$, 链式法则给出:

\[\frac{dy}{dx_i}=\frac{dy}{du_1}\frac{du_1}{dx_i}+\frac{dy}{du_2}\frac{du_2}{dx_i}+\cdots+\frac{dy}{du_m}\frac{du_m}{dx_i} \]

2、反向传播算法

2.1 反向传播解释

假设有函数为：

\[J(a,b,c)=3(a+bc),\text{合}u=a+v,v=bc \]

梯度计算图为：

反向传播计算：

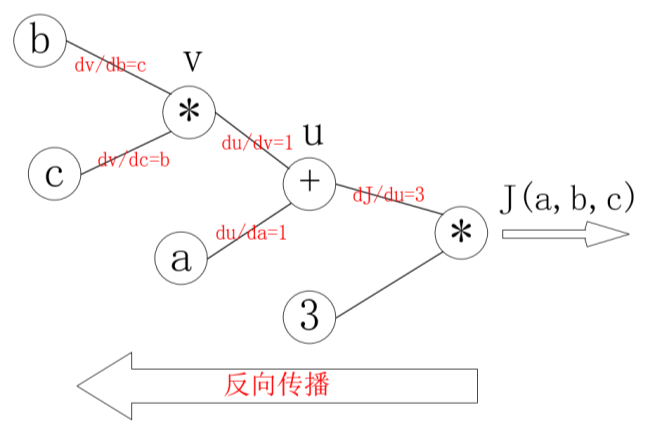
那么反向传播的过程就是一个上图的从右往左的过程，自变量$a,b,c$各自的偏导就是连线上的梯度的乘积。

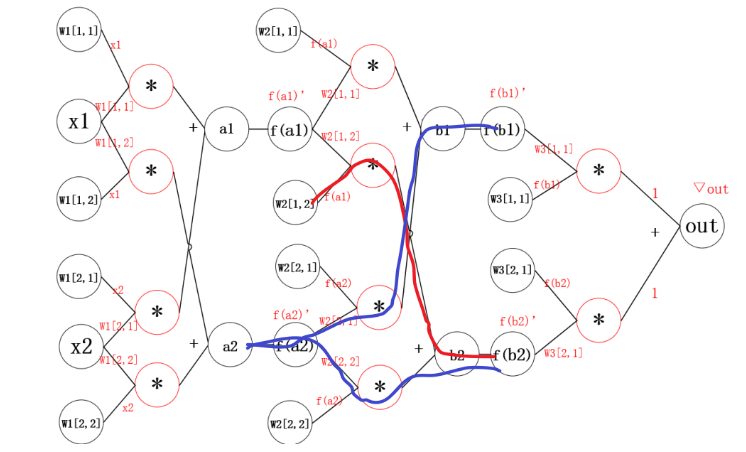
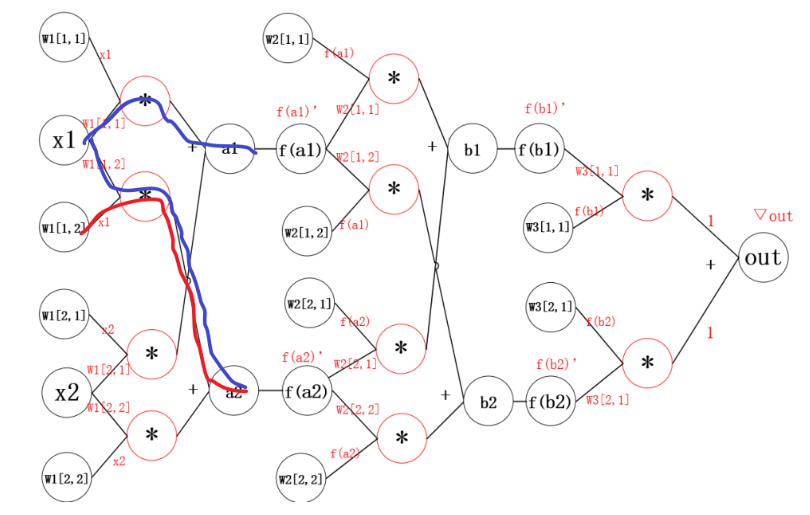
\[\begin{aligned} &\frac{dJ}{da} =3\times1 \\ &\frac{dJ}{db} =3\times1\times c \\ &\begin{aligned}\frac{dJ}{dc}\end{aligned} =3\times1\times b \end{aligned} \]

2.1 神经网络中的反向传播距举例

反向传播的思想就是对其中的某一个参数单独求梯度，之后更新。更新参数之后，继续反向传播。

3、线性回归举例

下面，我们使用一个自定义的数据，来使用torch实现一个简单的线性回归

假设我们的基础模型就是y = wx+b，其中w和b均为参数，我们使用y = 3x+0.8来构造数据x、y，所以最后通过模型应该能够得出w和b应该分别接近3和0.8

准备数据
计算预测值
计算损失，把参数的梯度置为0，进行反向传播
更新参数

import torch
from matplotlib import pyplot as plt


#1. 准备数据 y = 3x+0.8，准备参数
x = torch.rand([50])
y = 3*x + 0.8

w = torch.rand(1,requires_grad=True)
b = torch.rand(1,requires_grad=True)
print('初始w={}，b={}'.format(w,b))

def loss_fn(y,y_predict):
    loss = (y_predict-y).pow(2).mean()
    # 下述同等写法：[i.grad.data.zero_() for i in [w,b] if i.grad is not None]
    for i in [w,b]:
        # 每次反向传播前把梯度置为0
        # 在默认情况下， PyTorch会累积梯度，我们需要清除之前的值
        if i.grad is not None:
            i.grad.data.zero_()
    # 根据损失，反向传播计算梯度
    loss.backward()
    return loss.data

def optimize(learning_rate):
    # print(w.grad.data,w.data,b.data)
    # 由梯度与学习率，优化参数w，b的值
    w.data -= learning_rate* w.grad.data
    b.data -= learning_rate* b.grad.data

# 3000次epoch训练
for epoch in range(3000):
    #2. 计算预测值
    y_predict = x*w + b

    #3.计算损失，把参数的梯度置为0，进行反向传播
    loss = loss_fn(y,y_predict)

    if epoch%500 == 0:
        print(epoch,loss)
    #4. 更新参数w和b
    optimize(0.01)

# 绘制图形，观察训练结束的预测值和真实值
predict =  x*w + b

#使用训练后的w和b计算预测值
plt.scatter(x.data.numpy(), y.data.numpy(),c = "r")
plt.plot(x.data.numpy(), predict.data.numpy())
plt.show()

print("w",w)
print("b",b)

posted @ 2023-10-02 17:24 饮一杯天上水阅读(368) 评论(0) 收藏举报

jzYe