0.PTA得分截图

1.本周学习总结(5分)
学习总结,请结合树的图形展开分析。
1.1 二叉树结构
1.1.1 二叉树的2种存储结构
树的顺序存储和链式存储结构,并分析优缺点。
树的顺序存储结构
完全二叉树:按从上至下、从左到右顺序存储,n个结点的完全二叉树的结点父子关系
非根节点(序号i>1)的父结点的序号是 [i/2]
结点(序号为i)的左孩子结点的序号是2i([2i<=n] ,否则没有左孩子)
结点(序号为i)的右孩子结点的序号是2i+1([2i+1<=n] ,否则没有右孩子)
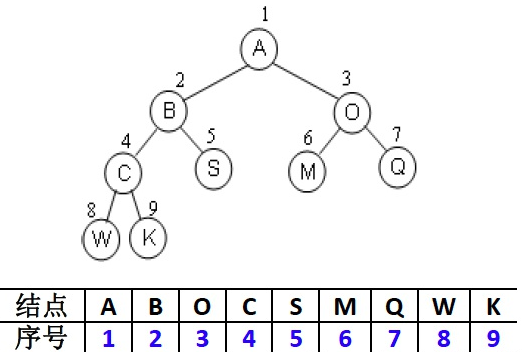
而一般树用顺序存储结构,较容易造成空间上的浪费。
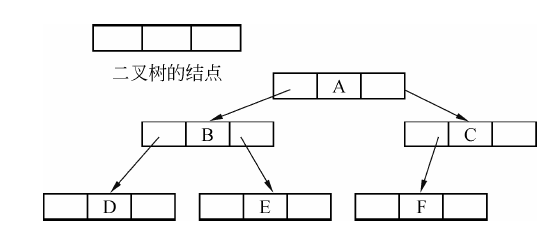
树的链式存储结构
每个结点的结构的代码定义
typedef struct TreeNode *BinTree;
struct TreeNode{
ElementType Data;
BinTree Left;
BinTree Right;
}
结构:
如图,从一个头结点开始,左孩子的指针指向一个子树,右孩子的一个指针指向一个子树,从而构成整棵树。
这就是利用链表的结构,来存储的树。
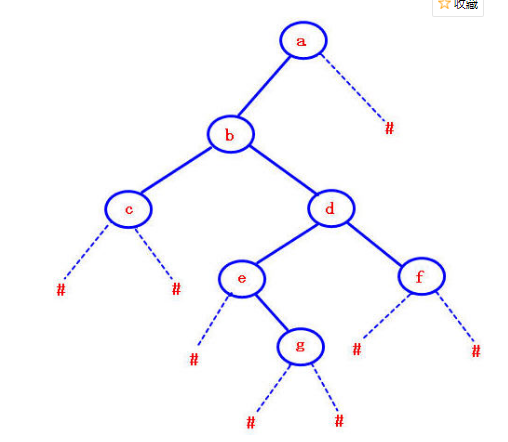
1.1.2 二叉树的构造
总结二叉树的几种构造方法。分析你对这些构造方法的看法。务必介绍如何通过先序遍历序列和中序遍历序列、后序遍历序列和中序遍历序列构造二叉树。
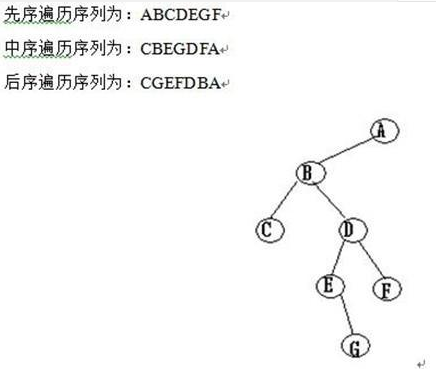
如图二叉树,前中后三种遍历都是利用递归的结构来进行遍历的,而先序遍历是先访问根节点,之后再访问其左子树跟右子树,同理中序遍历是先左子树
然后再进行根节点的访问跟右子树的访问,而后序则是先左右子树,后根节点。
而转换成构造,无非也是一种遍历,先创建一个树结点,然后看序列来创建左子树或者右子树,或者给根节点赋值。
先序遍历序列
代码实现
BTree CreatTree(char* str)//创建二叉树
{
if (str[i] == '#' || !str[i])
{
i++;
return NULL;
}
BTree T;
T = new TNode;
T->data = str[i++];
T->lchild = CreatTree(str);
T->rchild = CreatTree(str);
return T;
}
如果,则先创建根节点a,然后赋值,之后进入左子树的构造,在左子树里重复该模式,知道遇到#,构建右子树。
中序遍历序列
中序遍历是先进入左子树的构建,一直到#,然后才开始给根节点赋值,所以a就会在原来c的位置,进入右子树的构建,还是会优先构建左子树,所以c会出现在e的位置。
后序遍历序列
后序遍历如上所述,则先进入左右子树的构建,则赋值a后,因为原来的b有右子树,所以b结点并不会出现在原来的位置,而是会先进行左右子树的遍历,直到到达原来的g的位置,因为g的左右并无节点了,然后赋值后往上赋值,到原来的d的位置,但却不进行赋值,先构建右子树。
- 如此便是前中后三种序列的构建,实际的应用中,只需更改下赋值跟递归的顺序,差别其实不大。
1.1.3 二叉树的遍历
总结二叉树的4种遍历方式,如何实现。
二叉树的遍历(traversing binary tree)是指从根结点出发,按照某种次序依次访问二叉树中所有的结点,使得每个结点被访问依次且仅被访问一次。
四种遍历方式分别为:先序遍历、中序遍历、后序遍历、层序遍历。
先序遍历
前序遍历首先访问根结点然后遍历左子树,最后遍历右子树。在遍历左、右子树时,仍然先访问根结点,然后遍历左子树,最后遍历右子树。
若二叉树为空则结束返回,否则:
(1)访问根结点。
(2)前序遍历左子树。
(3)前序遍历右子树 。
已知后序遍历和中序遍历,就能确定前序遍历。
void preorder(BinTree BT)
{
if (!BT)
return;
if (!BT->Left && !BT->Right)
printf(" %c", BT->Data);
preorder(BT->Left);
preorder(BT->Right);
}
中序遍历
中序遍历首先遍历左子树,然后访问根结点,最后遍历右子树。若二叉树为空则结束返回,否则:
(1)中序遍历左子树
(2)访问根结点
(3)中序遍历右子树
已知前序遍历和后序遍历,不能确定中序遍历。
void inorder(BinTree BT)
{
if (!BT)
return;
inorder(BT->Left);
if (!BT->Left && !BT->Right)
printf(" %c", BT->Data);
inorder(BT->Right);
}
后序遍历
后序遍历是二叉树遍历的一种。后序遍历指在访问根结点、遍历左子树与遍历右子树三者中,首先遍历左子树,
然后遍历右子树,最后遍历访问根结点,在遍历左、右子树时,仍然先遍历左子树,然后遍历右子树,最后遍历根结点。
(1)若二叉树为空,结束
(2)后序遍历左子树
(3)后序遍历右子树
(4)访问根结点
void postorder(BinTree BT)
{
if (!BT)
return;
postorder(BT->Left);
postorder(BT->Right);
if (!BT->Left && !BT->Right)
printf(" %c", BT->Data);
}
层序遍历
层序遍历,主要运用队列的结构,来对一层一层的结点先后进行遍历,如果是同一层的结点,就先入队,然后读完上一层后,
就继续出队下一层的结点,然后再将下一层结点的左子树跟右子树的结点入队,再输出,以便能够达到保存一层层的结点进行输出
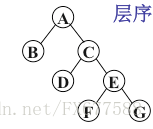
图的思维过程:
A入队
访问队首A,左儿子不为空,B入队,右儿子不为空,C入队,A出队
访问队首B,左右儿子为空,不用操作,B出队
访问队首C,同步骤2
访问队首D,同步骤3
访问队首E,同步骤2
访问队首F,同步骤3
访问队首G,同步骤3
遍历结果 ABCDEFG
void LevelTraversal(BinTree T)
{
if (!T)
{
cout << "NULL";
return;
}
BinTree p;
queue<BinTree>q;
q.push(T);
int flag = 1;
while (!(q.empty()))
{
p = q.front();//头结点
q.pop();//弹出头结点
if (flag)//访问结点
{
cout << p->Data;
flag = 0;
}
else if (!flag)
cout << " " << p->Data;
if (p->Left != NULL)
q.push(p->Left);
if (p->Right != NULL)
q.push(p->Right);
}
}
1.1.4 线索二叉树
线索二叉树如何设计?
按照某种遍历方式对二叉树进行遍历,可以把二叉树中所有结点排序为一个线性序列。在该序列中,除第一个结点外每个结点有且仅有一个直接前驱结点;
除最后一个结点外每一个结点有且仅有一个直接后继结点。这些指向直接前驱结点和指向直接后续结点的指针被称为线索(Thread),加了线索的二叉树称为线索二叉树。
建立线索二叉树,或者说对二叉树线索化,实质上就是遍历一颗二叉树。在遍历过程中,访问结点的场所是检查当前的左,右指针域是否为空,将它们改为指向前驱结点或后续结点的线索。
为实现这一过程,设指针pre始终指向刚刚访问的结点,即若指针p指向当前结点,则pre指向它的前驱,以便设线索。
另外,在对一颗二叉树加线索时,必须首先申请一个头结点,建立头结点与二叉树的跟结点的指向关系,对二叉树线索化后,还需建立最后一个结点与头结点之间的线索。

iThrNodeType *pre;
BiThrTree InOrderThr(BiThrTree T)
{ /*中序遍历二叉树T,并将其中序线索化,pre为全局变量*/
BiThrTree head;
head=(BitThrNodeType *)malloc(sizeof(BiThrType));/*设申请头结点成功*/
head->ltag=0;head->rtag=1;/*建立头结点*/
head->rchild=head;/*右指针回指*/
if(!T)head->lchild=head;/*若二叉树为空,则左指针回指*/
else{head->lchild=T;pre=head;
InThreading(T);/*中序遍历进行中序线索化*/
pre->rchild=head;
pre->rtag=1;/*最后一个结点线索化*/
head->rchild=pre;
};
return head;
}
void InThreading(BiThrTree p)
{/*通过中序遍历进行中序线索化*/
if(p)
{InThreading(p->lchild);/*左子树线索化*/
if(p->lchild==NULL)/*前驱线索*/
{p->ltag=1;
p->lchild=pre;
}
if(p->lchild==NULL)/*后续线索*/
{p->rtag=1;
p->rchild=pre;
}
pre=p;
InThreading(p->rchild);/*右子树线索化*/
}
}
中序线索二叉树特点?如何在中序线索二叉树查找前驱和后继?
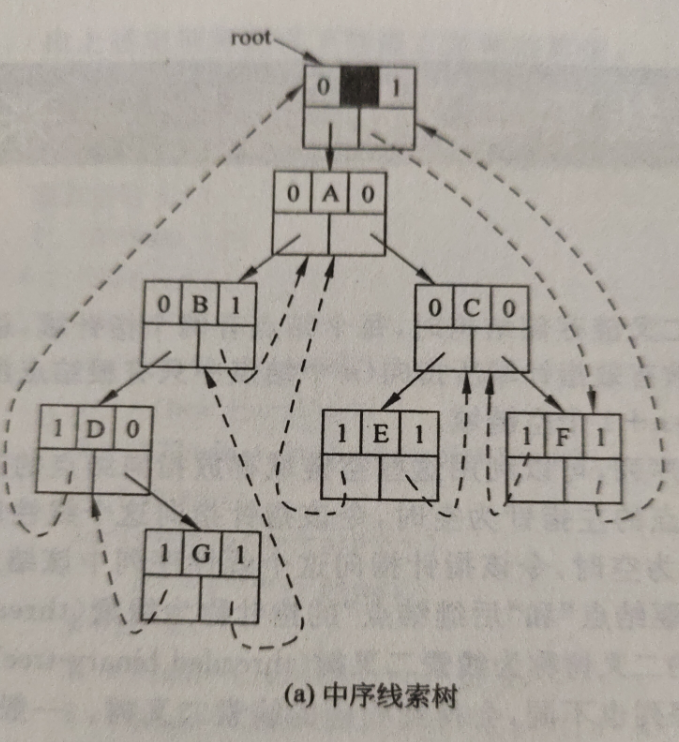
左指针为空时指向的便是前驱,右指针为空时指向的便是后继
1.1.5 二叉树的应用--表达式树
介绍表达式树如何构造
- 依次读取表达式;
- 如果是操作数,则将该操作数压入栈中;
- 如果是操作符,则弹出栈中的两个操作数,第一个弹出的操作数作为右孩子,第二个弹出的操作数作为左孩子;然后再将该操作符压入栈中。
这样下去,就可以建立一颗完整的表达式树。
如何计算表达式树
从操作数的栈中弹出两个数,再从操作符的栈中弹出一个符号,进行计算,得出的数再压入数栈中
如此循环,直至栈中清空,得出的最后一个数即为该表达式计算出来的结果。
1.2 多叉树结构
1.2.1 多叉树结构
主要介绍孩子兄弟链结构
孩子兄弟链表示法树的一种存储方式,每个结点由三部分组成:存储数据元素值的数据部分、指向它的第一个子结点的指针、指向它的兄弟结点的指针。
typedef struct node
{
char data;
struct node *sublist; //孩子链指针
struct node *link;//兄弟链指针
}BTNode;
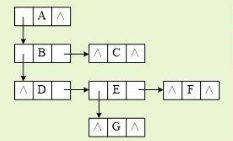
如此,以父节点指向第一个子节点,该层的其他结点存储为链表结构,即第一个子节点指向后续的结点。
这样存储方便了树的结构的构造,在多叉树的应用中,不需要在结构体中添加太多指向后继结点的指针元素。
但其劣势也很明显,不方便找到父亲结点。
1.2.2 多叉树遍历
介绍先序遍历做法
二叉树的先序遍历是优先输出根节点,后继续递归进入下一层的左孩子。
多叉树的遍历也类似,
1.访问根节点,
2.进行第一个孩子的优先的递归遍历,后进行后面其余孩子的递归遍历。
两者皆用递归的结构,且原理类似。
1.3 哈夫曼树
1.3.1 哈夫曼树定义
什么是哈夫曼树?,哈夫曼树解决什么问题?
给定n个权值作为n个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。
哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
霍夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树。所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数)。
树的路径长度是从树根到每一结点的路径长度之和,记为WPL=(W1L1+W2L2+W3L3+...+WnLn),N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,...n)。
可以证明霍夫曼树的WPL是最小的。
这种结构被用于电报的编码中,让使用频率高的用短码,使用频率低的用长码,以优化整个报文编码。
1.3.2 哈夫曼树构建及哈夫曼编码
结合一组叶子节点的数据,介绍如何构造哈夫曼树及哈夫曼编码。
哈夫曼树的树结构为二叉树,采用自下而上的构建方式
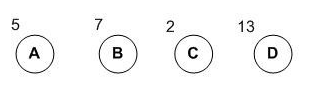
如图数据,找到两个最小的权的数据进行合并成一个子树
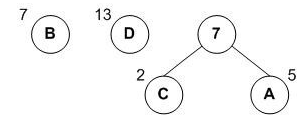
重复以上,再找到两个最小数进行合并

第三次进行合并

构成了最小带权路径的哈夫曼树
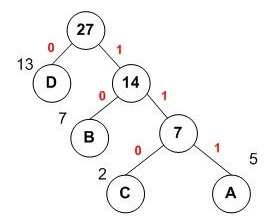
用0标注左枝干,1标注右枝干
则编码即为,头结点,到各字母的所经过的边的值的合并。
A,B,C,D对应的哈夫曼编码分别为:111,10,110,0。
1.4 并查集
在计算机科学中,并查集是一种树型的数据结构,用于处理一些不交集(Disjoint Sets)的合并及查询问题。有一个联合-查找算法(union-find algorithm)定义了两个用于此数据结构的操作:
Find:确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。
Union:将两个子集合并成同一个集合。
由于支持这两种操作,一个不相交集也常被称为联合-查找数据结构(union-find data structure)或合并-查找集合(merge-find set)。其他的重要方法,MakeSet,用于建立单元素集合。有了这些方法,许多经典的划分问题可以被解决。
为了更加精确的定义这些方法,需要定义如何表示集合。一种常用的策略是为每个集合选定一个固定的元素,称为代表,以表示整个集合。接着,Find(x) 返回 x 所属集合的代表,而 Union 使用两个集合的代表作为参数。
结构声明如下
typedef struct node {
int data; //结点对应人的编号
int rank; //结点秩:子树的高度,合并用
int parent; //结点对应双亲下标
} UFSTree; //并查集树的结点类型
初始化
void MAKE_SET(UFSTree t[],int n)//初始化并查集树
{
int i;
for(i=1;i<=n;i++)
{
t[i].data=0; //数据为该人的编号
t[i].rank=0; //秩初始化为0
t[i].parent=i;//双亲初始化指向自己
}
查找一个元素的集合
int FIND SET (UFSTree t[], int x) { //在x所在的子树中查找集合编号
if (x!=t[x]. parent) //双亲不是自己
return(FIND-SET(t,t[x] . parent); //递归在双亲中找x
else
return(x); //双亲是自己,返回x
}
合并两个元素各自所属的集合
void UNION(UFSTree t[], int x, int y) //将x和y所在的子树合并
{
x=FIND-SET(t,x); //套找*所在分离集合树的编号
y=FIND SET(t,y); //查找y所在分离集合树的编号
if (t[x].rank > t[y].rank) //y结点的秩小于x结点的秩
t[y].parent=x; //将y连到x结点上,*作为y的双亲结点
else //y结点的秩大于等于x结点的科
{
t[x].parent=y; //将x连到y结点上,y作为x的双亲结点
if (t[x].rank==t[y]. rank) //x和y结点的秩相同
t[y].rank++; //y结点的秩增
}
}
1.5.谈谈你对树的认识及学习体会。
2.PTA实验作业(4分)
此处请放置下面2题代码所在码云地址(markdown插入代码所在的链接)。如何上传VS代码到码云
2.1 输出二叉树每层节点
2.1.1 解题思路及伪代码
主要是利用队列的结构,使树按照层次来进行输出
伪代码
if 该树为空
输出NULL
创建树节点p , 队列q
h记录层数,next 保存队列进队的下一层的层数,n为遍历的该层的层数
for h =1 to 队列不为空
输出h
while 队列不为空且i<n
出队一个树节点赋给p
if p为有数据的结点
输出p的值
然后进行p的左右孩子的出队并且next++
i++
End While
n = next 将下层结点的数保存的该层进行下一轮遍历
next =0
end for
2.1.2 总结解题所用的知识点
所用的是树的构造还有树的层次遍历,队列的应用
2.2 目录树
2.2.1 解题思路及伪代码
2.2.2 总结解题所用的知识点
3.阅读代码(0--1分)
找1份优秀代码,理解代码功能,并讲出你所选代码优点及可以学习地方。主要找以下类型代码:
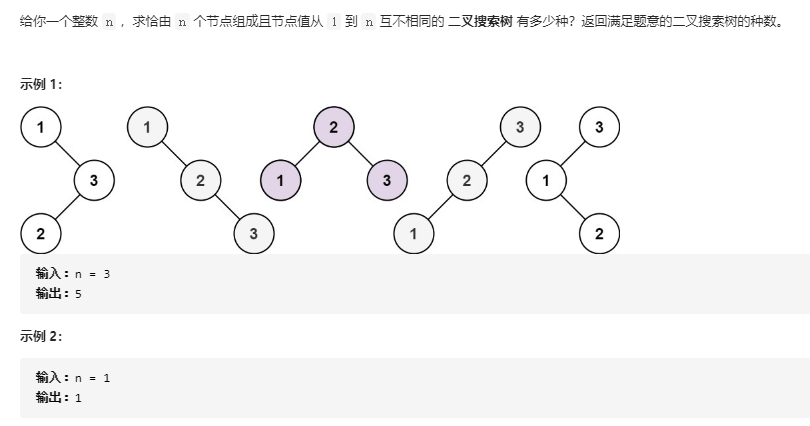
3.1 不同的二叉搜索树
可截图,或复制代码,需要用代码符号渲染。
int numTrees(int n) {
int G[n + 1];
memset(G, 0, sizeof(G));
G[0] = G[1] = 1;
for (int i = 2; i <= n; ++i) {
for (int j = 1; j <= i; ++j) {
G[i] += G[j - 1] * G[i - j];
}
}
return G[n];
}
3.2 该题的设计思路及伪代码
请用图形方式展示解决方法。同时分析该题的算法时间复杂度和空间复杂度。
动态规划法:
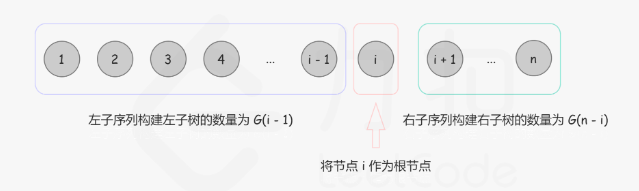
以i作为根节点,0-i-1作为左子树的根,i+1 -n 作为右子树的根
G(n): 长度为 n 的序列能构成的不同二叉搜索树的个数。
F(i, n)F(i,n): 以 i 为根、序列长度为 n 的不同二叉搜索树个数 (1≤i≤n)。
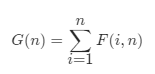

所以从头开始算G[]的值直至算至G[n]。
伪代码
定义数组G[]储存不同长度的搜索树的种类数量
初始化G
for 2 to n
for 1 to i
根据公式计算G[I]的值
返回G[n]

3.3 分析该题目解题优势及难点。
难点主要是对公式的推理分析,类似于前面所学的斐波那系数都是从头开始计算的,这种都是依赖与数学
的方式,找出规律整合出表达式。解题也给我提供了一种新的思路,不一定要用穷举的方式来做出题目,还可以对数据的结构进行分析,然后整合出更高效的表达计算方式。

 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号