NJUPT南京邮电大学数据结构实验一（线性表的基本运算及多项式的算术运算）

（仅提供思路，请勿照抄）

一、实验目的：
1、掌握线性表的两种基本存储结构及其应用场合：顺序存储和链接存储。
2、掌握顺序表和链表的各种基本操作算法。
3、理解线性表应用于多项式的实现算法。
实验内容及要求：
内容：实现顺序表和单链表的基本运算，多项式的加法和乘法算术运算。
要求：能够正确演示线性表的查找、插入、删除运算。实现多项式的加法和乘法运算操作。

二、算法设计
1.整体思路

2.多项式的相关操作：一元多项式的创建、输出、撤销以及两个一元多项式相加和相乘
流程图如下：

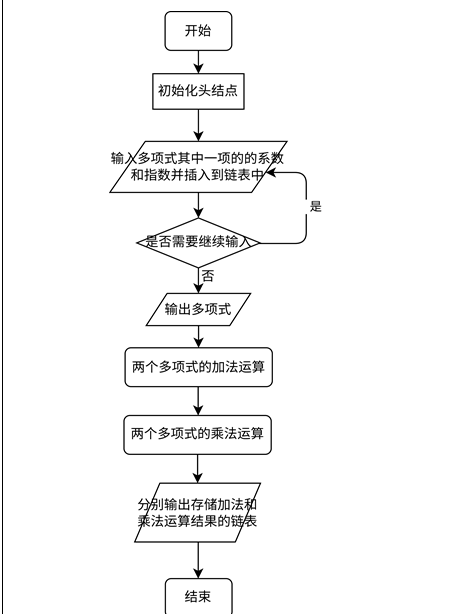
3.核心函数的解释及函数间的调用关系：
main函数里定义了一个顺序表list并调用Seq函数实现顺序表的相关操作
定义了一个表头结点的链表list2并调用Linked函数实现带表头结点的链表的相关操作
定义了多项式p1,p2,p3,p4并调用poly函数实现多项式的相关操作

①Seq函数：
调用InitSeq函数实现顺序表的初始化
调用InsertSeq函数实现顺序表的输入、插入元素（以插入0-9十个元素为例）
调用OutputSeq函数实现顺序表的输出
调用FindSeq函数实现顺序表的元素查找（以查找顺序表中下标为3的数为例）
调用DeleteSeq函数实现顺序表的元素删除（以删除0为例）
调用OutputSeq函数输出删除元素后的顺序表
调用DestroySeq函数实现顺序表的撤销

②Linked函数：
调用InitLinked函数实现带表头结点的链表的初始化
调用InsertLinked函数实现链表的输入、插入元素（以插入0-9十个元素为例）
调用OutputLinked函数实现链表的输出
调用FindLinked函数实现链表的元素查找（以查找链表中第三个元素为例）
调用DeleteLinked函数实现链表的元素删除（以删除0为例）
调用OutputLinked函数输出删除元素后的链表
调用DestroyLinked函数实现链表的撤销

③poly函数：
调用第一次init函数实现一元多项式p1的初始化和输入：在init函数内部调用insert函数进行多项式的项插入，调用print函数输出使得使用者能实时得知自己先前的输入结果
调用第二次init函数实现一元多项式p2的初始化和输入
调用print函数分别输出一元多项式p1和p2

加法和乘法的实现：
法1：借助数组来实现一元多项式的加法和乘法
调用pre函数做加法和乘法前的预处理：将输入的两个多项式的系数和指数用数组a、b存储
（在pre函数内部，分别遍历两个链表p1和p2，以多项式的指数为下标，系数为值存储到数组中，并用amax和bmax分别存储两个多项式里各项中最大的指数）
调用plus1函数实现p1和p2两个多项式的加法，并将和存储到p3函数中：在plus1函数内部从0开始，一直遍历ab数组到amax和bmax中的最大值，并将结果存放在链表p3之中）
调用time1函数实现p1和p2两个多项式的乘法，并将积存储到p4函数中：在time1函数内部二重循环遍历a数组和b数组，并将结果先存储在ti数组里，循环结束最后再存放到链表p4之中）

法2：直接使用链表来实现一元多项式的加法和乘法
plus2函数：先初始化p3的头结点，然后使用两个pNode指针a，b分别指向p1和p2的表头结点，然后一直循环，只有当两个指针都为空时才结束循环。循环内部进行判断，当一个指针为空时，把另一个指针指向的多项式的项插入至存放和的链表p3之中，当两个指针都非空时，判断哪个项的指数小，就插入至p3之中，若相等，直接将和插入到p3中，a，b指针指向下一项。（插入是调用的insert函数）
time2函数：先初始化p4的头结点，然后使用两个pNode指针a，b分别指向p1和p2的表头结点，然后使用二重循环，内部循环为p2链表，一直循环至b=NULL，外部循环为p1链表，一直循环至a=NULL，循环内部将a和b指向的项相乘并插入至存放和的链表p4之中。（插入是调用的insert函数）

最后调用destroy函数撤销p1和p2

3.分析算法的时间复杂度：
①和②主要是书上的代码，稍微修改了一点

①Seq函数：——时间复杂度：O(n)
调用InitSeq函数实现顺序表的初始化——时间复杂度：O(n)
调用InsertSeq函数实现顺序表的输入、插入元素——时间复杂度：O(n)
调用OutputSeq函数实现顺序表的输出——时间复杂度：O(n)
调用FindSeq函数实现顺序表的元素查找——时间复杂度：O(1)
调用DeleteSeq函数实现顺序表的元素删除（以删除0为例）——时间复杂度：O(n)
调用OutputSeq函数输出删除元素后的顺序表——时间复杂度：O(n)
调用DestroySeq函数实现顺序表的撤销——时间复杂度：O(1)

②Linked函数：——时间复杂度：O(n)
调用InitLinked函数实现带表头结点的链表的初始化——时间复杂度：O(1)
调用InsertLinked函数实现链表的输入、插入元——时间复杂度：O(n)
调用OutputLinked函数实现链表的输出——时间复杂度：O(n)
调用FindLinked函数实现链表的元素查找——时间复杂度：O(n)
调用DeleteLinked函数实现链表的元素删除——时间复杂度：O(n)
调用OutputLinked函数输出删除元素后的链表——时间复杂度：O(n)
调用DestroyLinked函数实现链表的撤销——时间复杂度：O(n)

③poly函数：——时间复杂度：O(n^2)或O(n3)
调用insert函数进行多项式的项插入——时间复杂度：O(n)
调用print函数进行多项式的输出——时间复杂度：O(n)
调用init函数实现一元多项式p1和p2的初始化和输入（时间复杂度不定，具体看用户的输入，用户输入一次是O（n）的时间复杂度）

加法和乘法的实现：
法1：借助数组来实现一元多项式的加法和乘法
调用pre函数做加法和乘法前的预处理——时间复杂度：O(n)
调用plus1函数实现p1和p2两个多项式的加法——时间复杂度：O(n)
调用time1函数实现p1和p2两个多项式的乘法——时间复杂度：O(n^2)
法2：直接使用链表来实现一元多项式的加法和乘法
调用plus2函数实现p1和p2两个多项式的加法——时间复杂度：O(n^2)
调用time2函数实现p1和p2两个多项式的乘法——时间复杂度：O(n^3)
最后调用destroy函数撤销p1和p2——时间复杂度：O(n)

4、实验结果与结论
（1）测试数据及运行结果
顺序表和链表的样例：

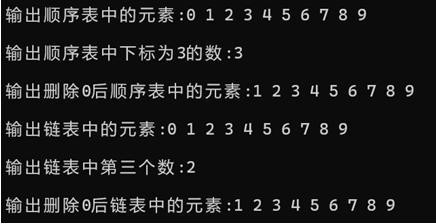
多项式的测试样例：

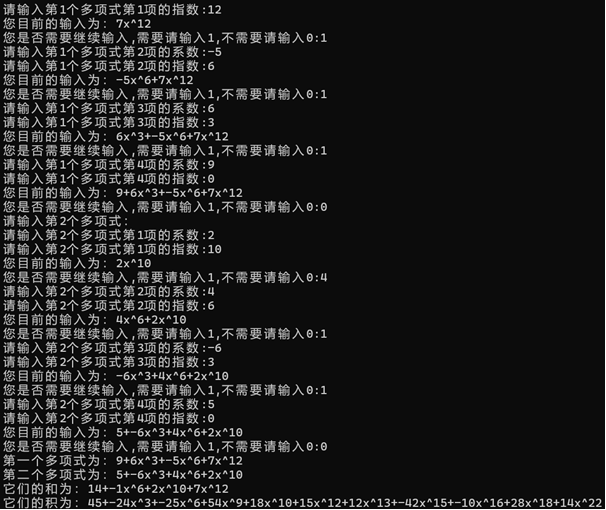
（2）实验相关结论
对于线性表的两种存储结构：顺序存储结构和链式存储结构
从时间复杂度上来看链表元素查找和撤销的时间复杂度比顺序表时间复杂度高，但是顺序表所占用的空间会更大一点，因为顺序表需要预分配一定长度的储存空间，还有空间溢出的问题。
另一个方面就是同样是Find元素查找函数，链表求的是第x个元素，比如存储0-9的链表，第3个元素是2；而顺序表的下标是从0开始的，存储0-9的顺序表，下标是3的元素就是3。
对于多项式的加法和乘法，我选择了两种方法，一种是法1：借助数组来实现一元多项式的加法和乘法，另一种是法2：直接使用链表来实现一元多项式的加法和乘法，法1的时间复杂度比法2低但是空间复杂度比法2高，属于是空间换时间的一种方法。两种方法都可以实现多项式的计算，具体采用哪一种还是看具体的需要。

三、实验小结
(一)实验中遇到的主要问题及解决方法
1.顺序表和链表
在顺序表和链表的代码撰写过程中，主要参考的是书上的代码，但是完全照抄书上代码的话肯定会报错，有几个地方需要修改：把Status、ERROR、OK等直接改为int、0、1使代码编写效率更高，还有需要区分开顺序表和链表的函数名称，虽然功能类似，于是我在原来的名称后面分别加上Seq和Linked加以区分，还有我用Seq和Linked函数替代main函数，并且其中调用的Init、Insert、Find、Output、Delete函数不能按照书上直接写Output(&list)，会报错，因为这几个函数都有返回值，所以需要改为if(Output(&list)==0)return;

2.多项式
输入问题：在编写多项式的相关代码的过程中，首先面临的问题是输入问题，如何去输入多项式？我最后决定以输入为标志，类似于do-while的方式，使用变量flag当作标志，每次输入多项式的一项之后输入flag，如果flag为1就继续循环，如果是0就跳出循环。

插入问题：如何将输入的多项式中的一项插入到链表中呢？这个地方我也调试了挺久的，有很多大大小小的问题，各种越界报错死循环。最后是使用指针p指向表头结点，然后用while循环从头结点开始寻找插入的位置，如果插入的结点的指数小于等于指针所指向的结点指数，就跳出循环，否则指向下一个。找到插入的位置之后，再进行判断如果两项指数相等就直接系数相加，否则插入新结点。

加法乘法算法问题：对于多项式的加法和乘法，我首先想到的是法1：借助数组来实现一元多项式的加法和乘法，将输入的两个多项式以数组的方法存储，相加时相同下标直接相加，相乘时直接相乘并按下标加入到另一数组之中，非常的方便，但是空间复杂度较高。

后来我又想到了另一种方法2：直接使用链表来实现一元多项式的加法和乘法，使用两个指针a，b分别指向两个多项式的表头结点，然后一直循环，只有当两个指针为空时才结束循环。在循环内部，对指针指向的多项式的项进行加和乘的操作，然后正好可以调用之前init函数所编写调用过的insert函数进行插入，大大提高了代码编写效率，但是这种方法的时间复杂度较高。

（二）实验心得
写代码需要有耐心且细心，面对编译失败时，多使用printf输出中间过程变量，或者使用单步调试功能，查找出来究竟哪里出了问题，然后进行修改。对于算法，如果时间复杂度或者空间复杂度太高，思考有无改进或者另一种思维的算法来提高效率。最终具体选择哪种方法需要看具体工程问题的需要。