BUAA-OO-2021 第三单元作业

BUAA OO 第三单元总结

设计策略与性能分析

本单元作业的核心就两个部分：数据的增删改查，简单图论。

关于数据的增删改查，大部分是根据 \(\text{id}\) 操作的，题目已经保证了 \(\text{id}\) 的唯一性。所以用 \(\text{HashMap}\) 模拟就好，所有操作 \(O(\) 常数\()\) 的时间复杂度就可以解决，没什么难点。

有一个需要注意的是 \(\text{Person}\) 收到的 \(\text{messages}\)，需要维护在头部插入新元素和查询前 \(4\) 个元素这两种操作，本人用了 \(\text{LinkedList}\) 维护，时间复杂度 \(O(1)\)。

另外题目还有一个查询 \(\text{query_name_rank}\) 的操作，该操作暴力遍历的时间复杂度是 \(O(|s|\ast n)\)，\(|s|\) 表示名字长度。不过题目限制了 \(|s|\le 10\) 且 \(\text{query_name_rank}\) 的出现次数 \(\le 333\)，所以还可以接受，如果放宽这些限制可能需要考虑平衡树或者字典树来维护。另外 \(\text{Java}\) 中的 \(\text{TreeSet}\) 虽然可以做到名次查询但不能用于本次操作，因为名字是允许有重复的但 \(\text{TreeSet}\) 不支持可重集。

关于图论，本单元作业涉及的操作有加边、维护图的连通性、最短路计算。由于没有删边操作，所以并查集维护连通性即可。路径压缩版和按秩合并版并查集均可，本人选择了路径压缩并查集，因为该类并查集代码量较少。然后题目还有询问连通块的数量，这个其实可以维护并查集的时候顺便维护。

关于最短路算法，直接 Dijkstra 算法即可，注意要用堆优化的版本，时间复杂度 \(O(m\log m)\)。如果用 \(O(n^2)\) 的 Dijkstra 算法会 \(\text{TLE}\)。

另外本单元作业的 \(\text{query_group_value_sum}\) 也是一个比较容易 \(\text{TLE}\) 的操作，如果按指导书的写法就是 \(O(n^2)\)。本人选择枚举该 \(\text{group}\) 中每个人的连边，再判断该边所连的另一个人是否属于该组来计算贡献，时间复杂度 \(O(n+m)\)。实际上也可以在每次 \(\text{add_to_group},\text{del_from_group},\text{add_relation}\) 操作时动态维护每个组的 \(\text{value_sum}\)，不过本人觉得这样会导致代码的可维护性下降，同时 \(O(m)\) 的时间复杂度已经满足了题目需求，所以并没有采取该方案。同理本人也从代码可维护性考虑没有动态维护每个组的平均年龄和年龄方差。

测试策略

本人在本单元强测互测中没有出现任何 \(\text{BUG}\)，同时在第一次作业成功 \(\text{hack}\) 两次，第二次作业成功 \(\text{hack}\) 一次。

本人第一次作业没有使用任何自测，第二次作业、第三次作业均使用了对拍测试。

本人没有用 \(\text{JUnit}\) 进行单元化测试的原因是 \(\text{JUnit}\) 要求测试者构造覆盖性较强的测试样例，首先这比较费时，其次我们对自己的代码进行测试时一般具有很强的主观性，通常自己写代码时没考虑的情况测试的时候也不会考虑。所以个人感觉编写代码的人和编写 \(\text{JUnit}\) 测试的人非同一人时才会有较好的 \(\text{Debug}\) 效果，而本单元测试条件有限，所以就放弃 \(\text{JUnit}\) 了。

于此相比，对拍就显得简便高效。不过对拍程序并没有帮本人 \(\text{de}\) 出任何 \(\text{BUG}\)，但帮助参加对拍的同学找出了不少 \(\text{BUG}\)，后来就演变成用自己的程序帮别人找 \(\text{BUG}\) 了，感觉自己成了小型自动测评机。

互测的时候采用黑盒测试，先用对拍程序 \(\text{hack}\) ，但总 \(\text{hack}\) 不到人，感觉自己房间的人都没什么明显错误。然后就是构成极端数据卡掉 \(O(n^2)\) 算法，这就是本人的主要 \(\text{hack}\) 手段。

架构设计

架构基本根据课程组给定 \(\text{JML}\) 进行的设计即可。

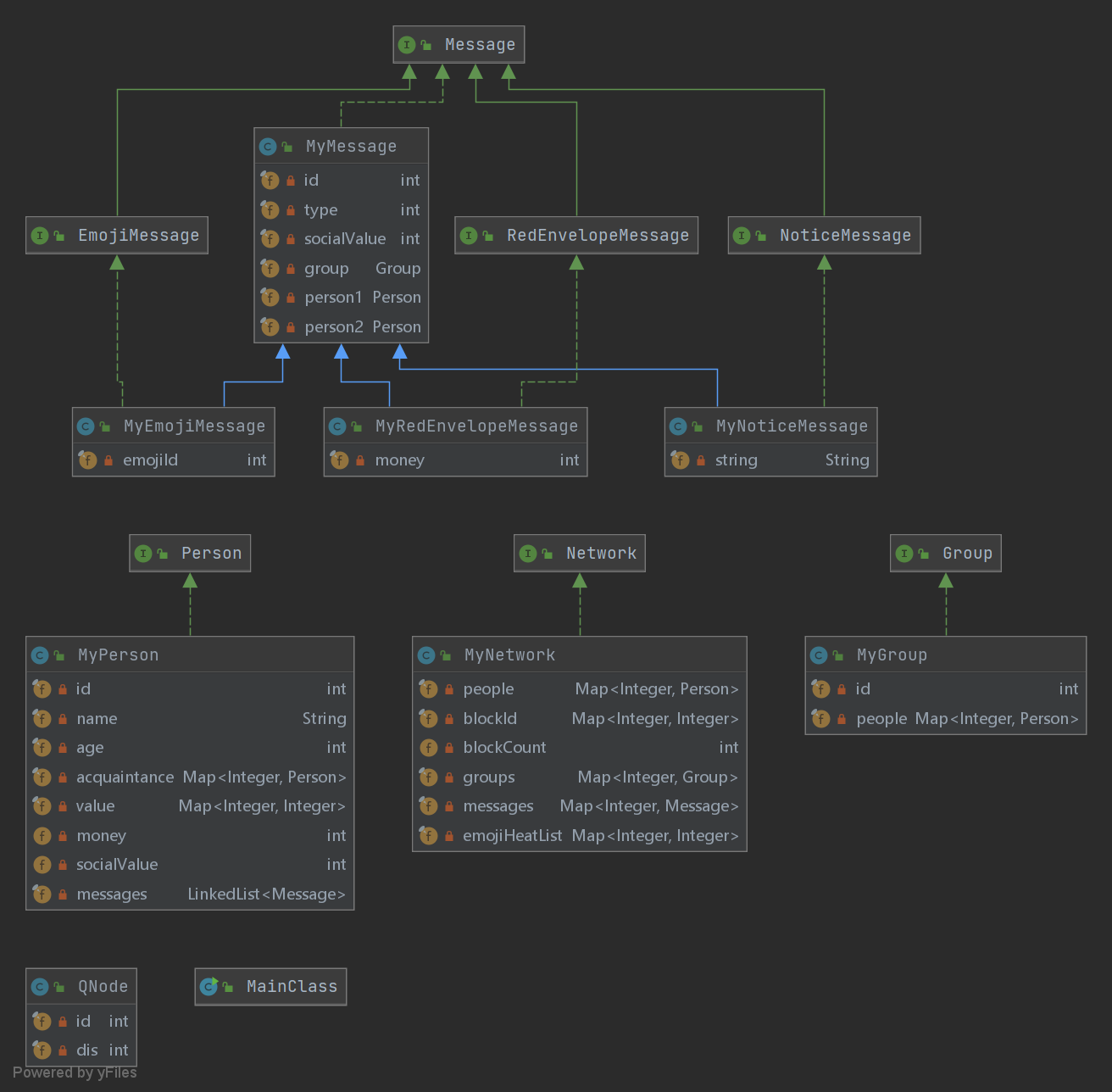
关于图的边用 \(\text{HashMap}\) 存储即可，至于连通性与最短路的问题在前面已经提过了。下面给出第三次作业的类图，其中唯一一个课程组给定的 \(\text{JML}\) 中没有的类 \(\text{QNode}\) 是堆优化 Dijkstra 算法需要用到的结点。

心得体会

本单元作业主要锻炼了本人的 \(\text{JML}\) 阅读能力以及对方法、数据规格的理解。作业代码本身的难度感觉比前两个单元低了不少，毕竟只需要根据 \(\text{JML}\) 进行简单模拟，然后稍微控制一下方法的时空间复杂度即可。