AStar 启发函数设计（老物）

作为我出山的第一篇日志，怎么也得写篇对得起我身份和地位的文章吧?

先容我吐槽一下不小心发的贴图，那个只是我不小心收藏了隔壁兄弟班的课表就别大家这么热情的 BB 我感到很有压力，额，废话不多说，立刻进入正题吧。

简单说一下 AStar （A*）算法，这是一种根据启发函数图遍历算法雏形。

举个栗子，如果你身处迷宫，但你知道出口的方向，那么你应该会尝试往出口方向前进，那么，第一种启发函数就被确定了，取出周围的点，根据一个欧拉距离运算来确定各个点距离出口还有多远，从而选择距离较近的点进行移动，这就是一种由启发函数进行导向的算法模型，假若还不了解什么是启发式搜索请自行移步到百度百科。

好滴，其实上面只是作为自己的一种理解让大家好明白我接下来要说明的内容是关于哪些方面的，如果不是计算机专业的同学看到这里，请自觉跳到最底通过看图例来感受一下启发式函数搜索的魅力吧(笑)。

通常的 A* 算法

通常的A*算法主要有两种估值函数，曼哈顿距离以及距离消耗步数进行结合，最终得到权值 F 可以做为下一步将要移动的位置，举个图例就是:

注:右图左上角为图形边界 30*30 ，右下角为搜索次数，起始点为(12，5)，终止点为(12，24)。最终搜索到的点为 423*4 （最大值）。
根据上图我们可见，通常 A* 寻路可以获得最短路径，但我这里的想法是应用在游戏寻路中，为了达到这个目的我不得不做出一些牺牲。
在做这个的优化的时候先在原有的基础上进行调整吧!

基础 A* 所用启发式函数为：

F = G + H
G = 移到到该处所需要走的步数
H = abs(this->x - Goal.x) + abs(this->y - Goal.y);
this 为当前位置的一个点，其中含有X，Y坐标信息，Goal为其所指向的目标点。

所以根据这个 F(x， y)我们可以得到上图的搜索情况，接着进行第一次简单优化。

首先我们构造的一个优先队列将所有搜索到的点入队依次按照 F 值排列，则这里可以提高 H 值的比重，让搜索向着目标方向进行，以减少点的进队，须知道一点就是每当搜索到一个点的时候就意味着有可能要对该点进行不大于 4 (基于 4 方向移动)的点展开搜索，这就是优化的方向，减少点进入优先队列，从而提高搜索效率。那么我现在做第一次优化。

F = sideMAX * H + G;//sideMAX为两边界的较大值

那么这时候的结果如下:
再来个图栗子吧~

此时，搜索会更加倾向于目标点从而一定程度上忽略了 G 值，这样搜索就会强调在大体方向，这样就完成了第一次优化，可喜可贺。
但是，我不认为这样就能够让大家满意了，我既然这么自信的发上来，那肯定是有点小九九的啦。

首先我要说明一点，曼哈顿距离 H = abs(this->x - Goal。x) + abs(this->y - Goal。y); 。

对目标距离并不敏感，因为它的值分布图是呈现菱形由目标点向外扩散的，那么，这就意为这个菱形的边的距离等效，在移动的时候会将这菱形的所有边长均录入优先队列，那么怎么办呢?（注:下文将构成菱形边长的所有点称为等效点）
首先，更换曼哈顿距离计算，将其换成欧拉距离（简单点说就是平面直角坐标系里的两点间距离公式）

D = sqrt(pow(Goal。x - this->x， 2) + pow(Goal。y - this->y， 2)); // sqrt 为开平方，pow(X，2) 为 X^2 方。

然而，这又有何卵用呢?首先，根据欧拉距离得到的等效点不同于曼哈顿的菱形，它的比较好看，就像一个圆形一样一圈圈由目标点扩散出去。

Let's look at it!

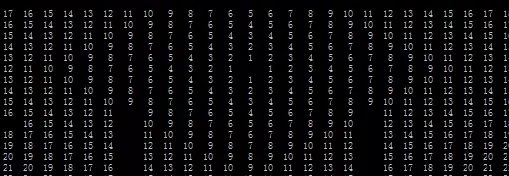
以上是曼哈顿距离值的情况

continue!

以下是欧拉距离值的情况

你会发现有一些些不同，首先欧拉数据类型比较小，存在浮点数，这就导致了它不能和 G 值共存(忘了 G 值意义的往回看看)，而曼哈顿为整数，呈现出有棱有角的形式。从图上看欧拉距离更趋近于圆形而非菱形，这就导致了在一些凹障碍的时候，两个的表示会不太一样，现在我们看看接下来的优化，好滴，这就再举个栗子!

左图为 F = G + sideMAX * H， 右图为F = D;

起始点为 (12，10) ，终止点为 (12，24) 。

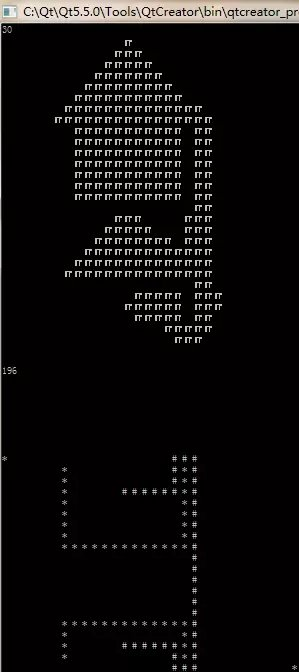
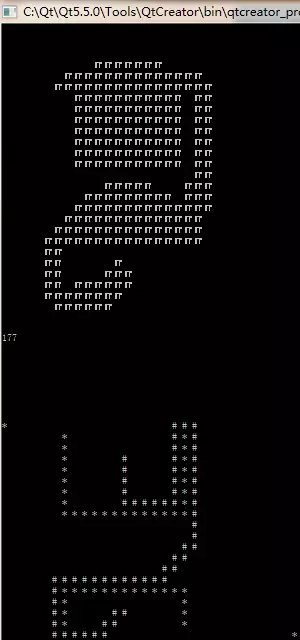
接着简单说明一下两者的区别的各个的优势，这也是我发这篇文章的最最主要的目的，先看左图搜索次数，其上图表示搜索了点的分布情况，这里我们在其右下角有一个路线的统计，这个 196 是统计着所有搜索过的路径，简单点看图，对，就左图中上图的方块数量，那个数量就等同于该值，这就可以作为两者的效率的一种简单的比较了(请允许我不用 O(N) 之类的说法)，那么开始好好说明一下吧~

效率上右图要比左图快得多，但由于不能和 G 值配套使用导致了其无法得到最短路径，这就是两者的区别，至于左图上方的尖角，那就是曼哈顿距离生成的菱形所导致的，这里我进行下一步优化~

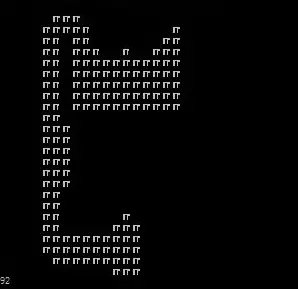
具体的启发式函数，就留给想知道的同学啦，虽然我也不太清楚有几个同学会喜欢研究这类玩意啦，但作为我出山开端，怎么也得给点拿得出手的东西吧~后续还有一些研究就放着了，待我成果能够确定下来为止我再进一步发出来吧 =- = ~