说说 HeapSort 堆排序思想,以及个人优化方案。(老物)
听说你要排上亿个数据之 HeapSort ?
前言 : 来来来,今天我们来说说一个用来排大量数据所用的基础比较排序吧~
注:阅读本文学习新技能的前置要求为:了解什么是二叉树及其数组性质,如果未达到要求的同学请直接看完图默默点右上角的×就好=- =~
在那之前我们先来看一个图
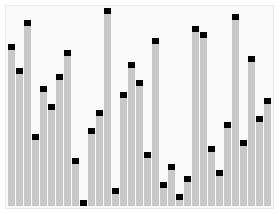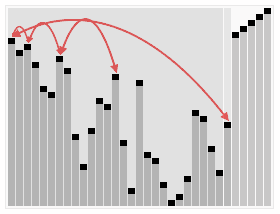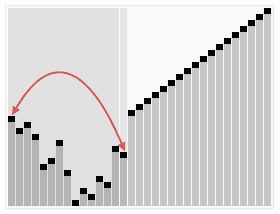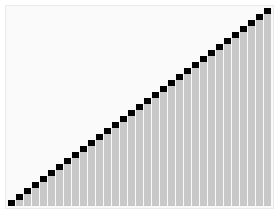
嗯,是不是很好玩?这玩意就是所谓的 HeapSort (堆排序)
而我们今天就来说说怎么像图例所示那样来进行我们的排序操作吧~
所谓的 HeapSort 呢,就是在一直做一件事,这件事用高雅点的名词就叫: HeapAdjust (调整最大堆)
在说明最大堆之前先提问,什么是堆呢?
沙堆,土堆,石堆,这些事物的特点是什么呢?
就好比金字塔,内容物是从底下到顶逐渐减少的.而我所说的最大堆,就是在说这样的一种堆
并且其最大堆的内容物(沙土石头或称 Key )呈现出其堆顶的价值(数值)最大,然后向下逐级递减.
那么,怎么产生这样的最大堆呢?
下面我贴一段来自于百度百科的代码吧~
百度百科 - 堆排序
// array 是待调整的堆数组, i 是待调整的数组元素的位置, length 是数组的长度
// 本函数功能是:根据数组 array 构建大根堆
void HeapAdjust(int array[], int i, int length)
{
for(int Child, Temp; 2 * i + 1 < length; i = Child)
{
//子结点的位置 = 2 *(父结点位置)+ 1
Child = 2 * i + 1;
//得到子结点中较大的结点
if(Child + 1 < length && array[Child + 1] > array[Child]) ++Child;
//如果较大的子结点大于父结点那么把较大的子结点往上移动,替换它的父结点
if(array[i] < array[Child]) Temp = array[i], array[i] = array[Child], array[Child] = Temp;
//否则退出循环
else break;
}
}
//堆排序算法
void HeapSort(int array[], int length)
{
int i;
// 调整序列的前半部分元素,调整完之后第一个元素是序列的最大的元素
// length / 2 - 1 是最后一个非叶节点,此处"/"为整除
for(i = length / 2 - 1; i >= 0; --i) HeapAdjust(array, i, length);
// 从最后一个元素开始对序列进行调整,不断的缩小调整的范围直到第一个元素
for(i = length - 1; i > 0; --i)
{
// 把第一个元素和当前的最后一个元素交换,保证当前的最后一个位置的元素都是在现在的这个序列之中最大的
array[i] ^= array[0], array[0] ^= array[i], array[i] ^= array[0];
// 不断缩小调整heap的范围,每一次调整完毕保证第一个元素是当前序列的最大值
HeapAdjust(array, 0, i);
}
}
所有要做的工作就在这里面,看上去是挺精简的了我觉得=- =.
那我们来说说它是怎么工作的吧~
首先 HeapSort 这个函数要做第一次预处理工作,这个工作的目的就是要把这个数组调整为最大堆
即倒序执行 HeapAdjust
但是并不是倒数第一个开始执行,而是倒数第二层中存在子节点的树结点开始(length / 2 - 1)。
这是什么意思呢?
这是因为HeapAdjust操作原理为:
首先选出其左右结点中较大的结点,然后将其与其父结点相比较,若大于则Swap之(此时构建最大堆).
然后对当前子结点执行上面的重复操作.
好的,当倒序到0的时候,就成功将这个最大堆建立起来了,现在需要做什么呢?
现在已知的条件是,顶端为这个堆的最大值,那么,这个最大值与数组最后一个元素交换(边界减一),
但此时这个最大堆又需要重新维护了,接着怎么做呢?
这时候就要立刻请出 HeapAdjust 大人,你要告诉它,你要调整的元素位置和它的边界。
让它把当前这个元素重新再调整为最大值,嗯,至此,感谢万能的 HeapAdjust 大人。
好吧,这就是堆排序的所有操作思想了.
至此,该篇已经结束,下面的是我个人的隐藏内容(/w \)(真有人会看到这里?没在开我玩笑吧~)
能看到这里的同学基本都是深爱着计算机的同学了,既然能看到这里,就让我来说点细节的问题吧~
其实,百度百科提供的代码很LOW的,下面就放出我的代码吧~
void HeapAdjust(int arr[], int pos, int len)
{
int keypos = (pos << 1) + 1, KeyElement = arr[pos];//keypos 为其左子节点位置, KeyElement 为当前需要调整位置的元素.
while(keypos < len)//检查左子结点是否越界.
{
if (keypos + 1 < len && arr[keypos] < arr[keypos + 1]) keypos++;//若右结点存在且比左结点更大则替换
if (KeyElement > arr[keypos]) break;//若不存在比KeyElement更大的的子结点则中断调整位置
arr[pos] = arr[keypos], pos = keypos, keypos = (pos << 1) + 1;//将当前节点覆盖其父节点,同时更新当前结点为其子节点
}
arr[pos] = KeyElement;//最后确定位置后归位
}
到这里就是我的改进版,接着,还有牺牲空间 N 的进一步优化。
while (true)
{
//因数组数据特殊性,当树结点单枝时一定存在左结点(pos + 1 >= max),则pos不变动
if(arr[pos] < arr[pos + 1] && pos + 1 < max) pos++;//若右结点存在且大于则替换为右结点
//将进一步移动到其子节点
arr[pos - 1 >> 1] = arr[pos], pos = (pos << 1) + 1;
//left and right node all is zero to break;
if (pos > max || (!arr[pos] && !arr[pos + 1]))
{
//assume zero is side element
arr[pos - 1 >> 1] = 0;
break;
}
}
目前还没发现有人和我做一样的改进诶嘿嘿,改进的原理为:
将堆顶元素抽走,接着下面的左右子结点较大的元素将被提上来,最后到了底(边界)时,将其赋值为0,在这之后,但凡两子节点为 0 (side element) 时将中断进一步对其子节点调整的操作。
理论上分析,这种牺牲空间N的做法比传统的(大量重复的 HeapAdjust )更为节省操作,代价就只需要浪费 N 的空间来存放数据.
这里小小提及一下现在C++的 STL sort()
它采用的是 QuickSort、 HeapSort 、 InsertionSort 的结合
总称 Introsort (内省排序)。
本文最后真挚地感谢 LYC 小队的 Y 同学日夜陪我研究和折腾,还有修改,表示没有他一同参与我感觉会很乏味的说,至于 L 同学则跑去打机了,先前 Astar 把他玩坏了,还是给他自由玩耍的空间好了= -=~
本想把改进的代码发布到 wiki 的,但现在想想还是留在这个没人关注的空间等到某天用上了再让它面世吧 =- = ~
两年后,嗯,当年的我学的都是些啥玩意!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号