二分图
最近一直在做图论专题,想出一篇图论算法总结,当然,这是后话了,今天先学二分图。
基本知识
二分图,又称二部图,是一类结构特殊的图。它的顶点集可以划分为两个互不相交的子集,使得图中的每条边都连接这两个集合之间的一对点,而不会连接同一集合内部的点。——OI wiki
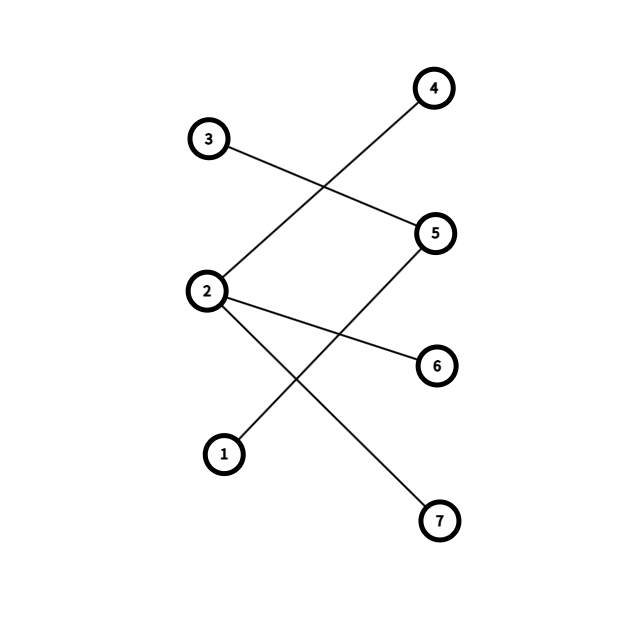
很明显能看出这个图分为左右两部分(当然不一定所有的图都是左右,可以上下,也可以是凌乱的,但你只要能将其整理出来可以分成如定义中的满足要求的两个集合,他就属于二分图),所以这是一个比较典型的二分图。
二分图的判定
如果给你一幅图(一般是无向图),让你去判断他是不是一个二分图应该如何做呢?
这里涉及到了二分图的几个性质,十分简单,我们从定义中就可以体会出来:
对于一个二分图 \(G\) 来说:
- \(G\) 一定是可以被用且仅用两种颜色着色的。
(什么是着色?听过四色定理吗?就是确保相邻的节点染上不同的颜色) - \(G\) 一定不存在奇环(就是奇数长度的环),因为如果存在,明显无法满足性质 \(1\)。
所以我们只需要简单利用这两条性质,就可以判断一个图是不是二分图了。
这是 OI wiki 的说法,但如果翻译成简单的语言,就是说我们拿到一个图,然后,对它进行以下操作:
存图
后面还会讲,这里先说最基础的
//我们以最简单的存图(链式前向星)为例。
cin >> n >> m;
for(ll i = 1;i <= m;i++){
ll u,v,w;
cin >> u >> v;
add(u,v);
add(v,u);
}
遍历未染色节点
我们遍历整个图上的节点,如果发现没染色过的点,那我们就 DFS 进行染色。
ll col[N] , ans /*,sum[2]*/;
for(ll i = 1;i <= n;i++){
if(!col[i]){ //未被染色
//sum[1] = sum[0] = 0;
col[i] = 1 + (1 ^ 1);
dfs(i , 1 ^ 1);
// ans += min(sum[1] , sum[0]); 按题目要求处理
}
}
DFS 节点染色
然后简单进行深搜,不过多赘述。
inline void dfs(ll x , ll c){
sum[c]++;
for(ll i = first[x];i;i =edge[i].next){
ll v = edge[i].to;
if(!col[v]){
col[v] = 1 + (c ^ 1);
dfs(v , c^1);
}else{
if(col[v] == c + 1){
cout << "Impossible";
exit(0);
}
}
}
}
如果发现一个节点染过色了,且和当前节点颜色相同,那就说明存在奇环,肯定不是二分图。
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define ll long long
#define dbug(x) (void)(cerr << #x << " = " << x << endl)
ll n,m;
const int N = 1e5+86;
struct node{
ll next , to , w;
}edge[N*2];
ll first[N] , cnt;
inline void add(ll u,ll v){
cnt++;
edge[cnt].to = v;
edge[cnt].next = first[u];
first[u] = cnt;
}
ll col[N] , ans , sum[2];
inline void dfs(ll x , ll c){
sum[c]++;
for(ll i = first[x];i;i =edge[i].next){
ll v = edge[i].to;
if(!col[v]){
col[v] = 1 + (c ^ 1);
dfs(v , c^1);
}else{
if(col[v] == c + 1){
cout << "Impossible";
exit(0);
}
}
}
}
int main() {
cin >> n >> m;
for(ll i = 1;i <= m;i++){
ll u,v,w;
cin >> u >> v;
add(u,v);
add(v,u);
}
for(ll i = 1;i <= n;i++){
if(!col[i]){
sum[1] = sum[0] = 0;
col[i] = 1 + (1 ^ 1);
dfs(i , 1 ^ 1);
ans += min(sum[1] , sum[0]);
}
}
cout << ans;
return ~~ (0 ^ 0);
}
上述过程那就是二分图染色的基本流程了,除了可以用于二分图判断,还可以对题目具体要求进行相关处理,这部分内容较为简单,所以我们只来着重讲一讲其中的存图部分。
对于一个题来说,出题人肯定会设置一个情景,每道题的输入格式也因题而异,那为了让这个题不那么容易看出是一个二分图的话,他一般就不会直接给你一个图论题,那这个时候我们就要对题面输入进行客制化的处理(绝大多数情况就是这个图的节点编号是重复使用的,具体我说的是什么意思,随便找一道题看看自己体会)。
我们介绍一种方法,将节点重新分区编号,没错就是这么暴力,如果两个部分的节点编号相同的话,我们就将其中一部分的点的编号整体下标向后挪动一个分区。
注意,此时的数组大小也要成倍增加。
ll n;
cin >> n; //一个简单的例子
for(ll i = 1;i <= 2 * n;i++){
ll a,b;
cin >> a >> b;
add(i , a + 2 * n);
add(i , a + 3 * n);
add(i , b + 2 * n);
add(i , b + 3 * n);
}
二分图最大匹配
匹配 或是 独立边集 是一张图中不具有公共端点的边的集合。
显然,一般图的匹配问题我们会涉及到网络费用流,带花树算法等等等等,就比较困难了,但是在二分图中,最大匹配问题还是比较好解决的。
前置知识
对于图 \(G\) 和它的一个匹配 \(M\)(一定要理解这是一个相对概念),我们可以定义如下两种(简单)路径:
- 交错路(alternating path)是由匹配边与非匹配边交错而成的路径;
- 增广路(augmenting path)是始于未匹配点且终于未匹配点的交错路。
我们不难发现,从定义来看,一条交错路内部必定暗含这一个匹配,所以找到一条交错路,就能找到一个匹配(因为他是相对概念,现有一个匹配,对于这个匹配才会有一条交错路)。
而增广路呢,我们也可以发现,对于一个匹配,增广路始于未匹配点,终于未匹配点,且他是一条交错路,那我们不难发现,原匹配在以它对应增广路为全集的补集也是一个匹配,可能有些绕,翻译过来就是,如果对于一个匹配我们能找到他的增广路径,那我们一定可以在这个图中找到比这个匹配更大的一个匹配。
所以如何找到最大匹配,在二分图中就转换为了找增广路径。
Berge 引理:对于图 \(G\) 和它的一个匹配 \(M\),匹配 \(M\) 是最大匹配,当且仅当不存在相对于匹配 \(M\) 的增广路。
实现流程
解决这个问题,我们要学习一下一个新的算法,叫做 Kuhn 算法。
我看到网络上许多博客说这是匈牙利算法,也不能说错误,只不过匈牙利算法解决的是二分图最大权匹配,我们所使用的 Kuhn 算法解决最大匹配问题,其实质就是一部分或者说狭义上的匈牙利算法。
这个算法的实质就是 DFS。为了求出最大匹配,算法依次枚举所有顶点,求出从它出发的一条增广路,并进行 DFS 增广。
这里不难发现,我们如果规定都从二分图左部选取未匹配的点,然后进行增广,最后如果是一条增广路一定会再次回到左部的另一个未匹配点。或者说,从左部的未匹配点出发的增广路(或者任何一条交错路)中,只能沿着非匹配边从左部点到达右部点,再沿着匹配边从右部点到达左部点。
因此,我们只需要处理一半,即只在左部选取未匹配点进行增广。
代码实现
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define ll long long
#define dbug(x) (void)(cerr << #x << " = " << x << endl)
const int N = 5e4+86;
struct node {
ll next, to;
} edge[N];
ll first[N], cnt;
inline void add(ll u, ll v) {
cnt++;
edge[cnt].next = first[u];
edge[cnt].to = v;
first[u] = cnt;
}
ll ans;
ll oside[N], book[N];
inline bool find(ll x) {
book[x] = 1;
for (ll i = first[x] ; i; i = edge[i].next) {
ll v = edge[i].to;
if (!oside[v] || (!book[oside[v]] && find(oside[v]))) {
oside[v] = x;
return true;
}
}
return false;
}
int main() {
ll n, m, e;
cin >> n >> m >> e;
for (ll i = 1; i <= e; i++) {
ll u, v;
cin >> u >> v;
add(u, v + n);
}
for (ll i = 1; i <= n; i++) {
for (ll j = 1; j <= n + m; j++) {
book[j] = 0;
}
if (find(i)) ans++;
}
cout << ans;
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号