数列详解

前言

本来这篇文章是不会诞生的，因为在我眼中，数列本应是一个很简单的知识点，很多常见的数列本应作为常识而众人皆知，但最近在偶然情况下发现很多人竟然都没听说过斐波那契数列，例如一位姓王的同学……

于是这篇文章就诞生了，博主搜罗大量论文文献，网站详解，综合于此，旨在一文讲透初中大部分数列知识。

对数列的认识

定义

数列（sequence of number），是以正整数集（或它的有限子集）为定义域的一列有序的数。数列中的每一个数都叫做这个数列的项。排在第一位的数称为这个数列的第 \(1\) 项（通常也叫做首项），排在第二位的数称为这个数列的第 \(2\) 项，以此类推，排在第 \(n\) 位的数称为这个数列的第 \(n\) 项，通常用 \(a_n\) 表示。——引自百度百科

从这段文字中，我们需要认识很多熟悉的概念。

• 项：即数列中的每一个数
• 项数：数列中项的个数
• 首项：数列的第一项
• 尾项：也称末项，数列的最后一项（注意：很多的数列项数为 \(+\infty\) ，即无穷数列，此时并没有一个严格意义上的尾项，多数时候尾项只针对于一个数列被我们所研究的区间段的最后一个）

表示

数列常用{}来表示，例如{0,1,2,3,4,5…}可表示自然数列。

有人会说，这不就是集合吗？

这种说法便是大错特错的，数列的表示方法和集合是有本质性区别的，最明显的区别就是数列具有顺序性。

举个例子：

{1,2,3}和{3,2,1}可以表示同一个集合，但却表示了完全不同的两个数列，这便是数列的顺序性。

另外，数列中的数不具有集合的互异性，也就是说，数列中可以出现相同的数。

再如：

{0,1,0,1,0…}就是一个合法的数列，但不能称之为一个集合，因为其中含有相同重复出现的数。

性质

数列的规则性

除了上述提到的顺序性和可重复性，数列还有一个重要的性质，即规则性

注意，这是数列的学习中最重要的一个内容。

对于一个数列，他通常会存在一个规则，也就是用于计算每一项值的方法，若不存在这样的一个规则，那这个数列的研究大概率是没有任何价值的。

例如：

对于一个公差为 \(2\) 的等差数列{1,3,5,7…}（也就是正数奇数数列）：

我们便可以轻而易举的得出其适用的规则是：从 \(1\) 开始，每项加 \(2\)。

注意我的用词——规则是，而有时候，会表述成一个规则是，这表示并不是唯一的规则，一个数列一般给出形式是带有省略号的，我们在无法确定数列中的全部元素时，规则有时并不只有一个（但上述例子已经指明是确切的奇数数列，所以规则确实是唯一的）。

例如数列{3,5,7…}，这只是一个普通的数列，并没有过的进行描述，言外之意就是：

这个数列若继续往后写，可以写成{3,5,7,11,13,17,19…}，这时对这个数列的规则就可以表述成除了 \(2\) 以外的所有素数，但如果他继续写成了{3,5,7,9,11,13,15…}，是不是就又变成了我们所熟知的正数奇数数列，只不过不包含数字 \(1\)，这可是完全不同的两个数列。

因此，数列的规则不具有单一性，所以最好说："数列的一个规则是"，而不要说："数列的规则是" （除非我们知道那规则是唯一的正确规则）。

数列规则的表示

• 通项公式

  对于这个规则，我们需要用一个公式来表示他，一般是一个含有 \(n\) 的代数式，\(n\) 就表示任何一项的序数，这也就是我们常说的通项公式。

  通项公式是我们研究数列的得力助手，对于一个数列，只要推导出了他的通项公式，就可以较为轻易的求出他的许多信息。

  还是例如我们的正数奇数序列：{1,3,5,7…}

  他的规则是：从 \(1\) 开始，每项加 \(2\)。

  那我们用含 \(n\) 的代数式可以把上述规律表示为：\(a_n=2n-1\)，

  这便是通项公式。

• 递推公式

  递推公式不如通项公式实用，甚至我感觉有很多人都没有听过这一名词，但从某些角度，递推公式也是不可缺少的。

  为什么这么说呢，因为递推公式具有更普遍性，凡是有通项公式的数列，都会有其递推公式，但没有通项公式的数列，有的也会有递推公式，注意，也不是全部，有些数列的规律性不明显，也没有递推公式，例如我们所熟知的素数数列{2,3,5,7,11,13…}

  那么什么是递推公式呢？如果一个数列的第 \(n\) 项与它前一项或几项的关系可以用一个式子来表示，那么这个公式叫做这个数列的递推公式。

  实践出真知，著名的斐波那契数列的递推公式就可以表示为：\(a_n=a_{n-1}+a_{n-2}\) （注意，其实是片面的，详细请在“常见数列详解”见）。

  而他的通项公式却是：

  \(\begin{align} {a_n =\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^{n}-\left(\frac{1-\sqrt{5}}{2}\right)^{n}\right]} \end{align}\)

  所以，在一些特定的数列中，递推公式表示会简便一些，但要明白一点，递推公式靠人力是无法求出一些较大的值的，所以常需借助计算机辅助，这一性质，就注定了递推公式的实用性远不如通项公式。

基本运算

数列的基本运算，常见的有两种：求和与求第 \(n\) 项

求和

这个运算十分暴力，就是将数列中的元素都加起来的和。

求和分为求全部和、求区间和、求级数。

这里我们不得不提一下数列的分类。

数列按照元素个数，可分为两类：有穷数列和无穷数列，这一概念非常好理解，一个数列若项数为 \(+\infty\)，则称其为无穷数列，否则为有穷数列。

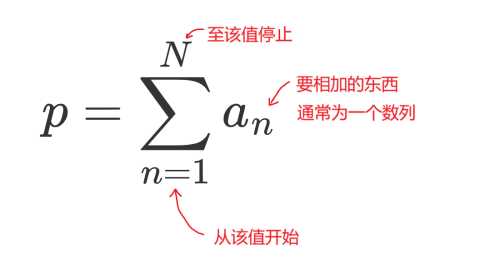
我们常用符号 \(\sum\) 来表示数列的求和运算，读作Sigma，这个符号的意思就是”加起来“，我们可以用一张图来了解一下该符号的使用：

再举一个例子：

给出一个数列 {\(a_n\)} 为{2,4,6,8,10…}，此时：

\( \begin{align} p = \sum_{n=2}^5{a_n} = 4+6+8+10 = 28 \end{align} \)

该式即表示求数列中第 \(2\) 项到第 \(5\) 项的和，即 \(a_2+a_3+a_4+a_5\)。

虽然可能比较难以理解，但由于实用性不是很高，就不再说了，想深入了解的可以自行查找资料

全部和

而求和的运算中，求全部和只能针对与有穷数列，也非常简单，这里不做过多解释。

级数

级数这一概念非常有趣，这个词的解释就是无穷个有规律的项的和，即无穷数列的所有元素之和我们称之为级数，注意，这个词听起来好像是一个数列的名字，但其实它是指数列的和。

一个无穷数列的级数可以表示为：

\( \begin{align} p = \sum_{n=1}^\infty{a_n} \end{align} \)

级数可以分为两种，即收敛性级数和发散性级数。

• 收敛性

  通常情况下，级数并没有一个可计算的值，但一些级数的总和非常趋近于一个有限值，这类级数便能叫做收敛的。

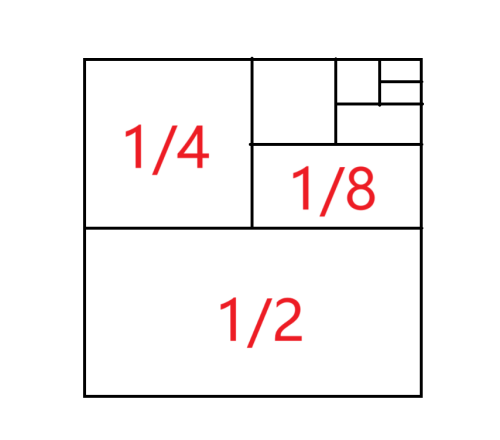
  举个例子，数列\(\left\{ \frac{1}{2},\frac{1}{4},\frac{1}{8},\frac{1}{16}… \right\}\)

  这个数列非常神奇，我们用一张图来表示一下这个数列的来源：

  

  这个数列的和便是：
  \( \begin{align} p = \sum_{n=1}^\infty{\frac{1}{2^n}} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} … = 1 \end{align} \)​

  有人可能已经看出来了，结合这个数列的实际意义，假设大正方形面积为 \(1\) ，那么这些小的矩形面积之总和会无限的趋近于 \(1\)​。

• 发散性

  这个便比较常见了，若一个数列并不收敛，级数便叫做发散的。

  就例如一个很普通的自然数列{1,2,3,4…}，它的级数就很难用一个有限的值来表示，而是接近于 \(+\infty\)。

  像这类发散性的级数，非常之常见，故它的级数也没有太大的研究价值，便也不过多赘述了。

区间和

这便是求和部分的重点内容了，因为如果题目中给定一个数列，求全部和和级数一般是不现实的，在考试题目中，最常见的就是等差数列和等比数列求和，这一部分会在后面的“常见数列详解”中提到。

在题目中，通常会给定一个数列 {\(a_n\)} ，若将这个数列的第 \(i\) 项记作 \(a_i\) 的话，给定两个整数 \(l\) 和 \(r\) ，要求 \(a_l\) 到 \(a_r\) 的区间和，用符号语言表示：

\( \begin{align} p = \sum_{n=l}^r{a_n} \end{align} \)

至此，求和部分结束。

求第 \(n\) 项

这亦是一个重点考题，从考察频率上看，甚至要多于求和部分。

但是，这一部分也非常简单，就一个要点：推导出通项公式。

若一个数列并没有通项公式，那求第 \(n\) 项便会难上加难，一般来说不会轻易考察。

我们来举一个例子详细说明一下如何求第 \(n\) 项。

再例如正数奇数数列（老演员了）：{1,3,5,7……}

通项公式轻易可推导为 \(a_n=2n-1\)

则求第 \(n=5\) 项时，可表述为：\(a_5=2\times 5 -1 = 9\)

则第五个奇数是 \(9\) ，是不是非常简单。

总的来说，求第 \(n\) 项，就是将对应的 \(n\) 值代入通项公式求值。

引申一下，那如何求一个数 \(n\in\) {\(a_n\)} 在数列的第几位呢，即若给定一个数，保证他处于数列中，那他在这个数列的第几位呢？

也很简单，列一个方程就好了，例如我要求 \(201\) 在正数奇数数列中的位置，就将 \(a_n\) 用 \(201\)代替列出方程求解就好了：

\( \begin{align} a_n = 2n-1 \\ 201 = 2n - 1 \\ n = 101 \end{align} \)

即说明，\(201\) 处在第 \(101\)​ 位。

那么求第 \(n\) 项部分到此为止，进入更为实用的常见数列详解部分。

常见数列详解

等差数列

定义

这无疑是我们在数列的学习中最重要的数列，也是最为常见的数列，例如自然数列，奇数数列，偶数数列……

一般形式表示为{a,a+d,a+2d,a+3d…}。

下一个定义：等差数列就是相邻两项之差为常数的数列，该常数称为公差，这一定义可用递推公式表示为：\(a_n - a_{n-1} = d(n \ge 2)\)，\(d\) 为常数。

简单的说，就是从第一个数开始，每次加一个等值，直到永远（所以说，等差数列一般是一个无穷数列）。

通项公式

一般有三种表示形式（实用程度依次递减）：

• \(a_n = a_1 + (n-1)d\)
• \(a_n = pn + q\)
• \(a_n=a_m + (n-m)d\)​

这里提供给一种较易理解的推导方式：

以该数列 {\(a_n\)} 为例{3,5,7,9…}：

先知道其公差 \(d\) 为 \(2\) （十以内加减法不会就不用学习本文章了），求出当\(n = 1\) 时 \(d\times n\) 的值为 \(2\)，与 \(a_1\) 作差为 \(3 - 2 = 1\)，所以通项公式即可表示为 \(a_n = 2n + 1\)。

其中 \(n\) 的系数 \(2\) 即为公差，后面加的 \(1\) 就是与第一项作的差。

计算公式

有些人小学或许还听说过求末项公式，求公差公式等等，但其实完全没必要记这些，因为都可以利用通项公式计算，而且效率可能更高，真正需要记忆的，是以下列出的这些。

求和

表示为：

\( \begin{align} \sum_{k=0}^{n-1}{(a + kd)}=\frac{n}{2}(2a+(n-1)d) \end{align} \)​

推导这个公式很有意思，首先，我们设数列的和为 \(S\)，则 \(S = a + (a+d)+…+(a+(n-2)d)+(a+(n-1)d)\)

接下来，我们运用加法交换律（这不至于不会吧？）将 \(S\) 反着加一遍：\(S = (a+(n-1)d)+(a+(n-2)d)+(a+d)+a\)

将两次的结果相加得到

	\(S\)	\(=\)	\(a\)	\(+\)	\((a+d)\)	\(+\)	…	\(+\)	\((a+(n-2)d)\)	\(+\)	\((a+(n-1)d)\)
\(+\)	\(S\)	\(=\)	\((a+(n-1)d)\)	\(+\)	\((a+(n-2)d)\)	\(+\)	…	\(+\)	$(a+d) $	\(+\)	\(a\)
	\(2S\)	\(=\)	\((2a+(n-1)d)\)	$+ $	\((2a+(n-1)d)\)	$+ $	…	$+ $	\((2a+(n-1)d)\)	\(+\)	\((2a+(n-1)d)\)

会发现最后的结果每一项都是一样的！！

所以：

\( \begin{align} 2S & = n(2a+(n-1)d) \\ S & = \frac{n}{2}(2a+(n-1)d) \end{align} \)

或许有人看不懂，那这个公式也可等价于高斯求和公式，即首项加末项的和乘项数的积的一半：

\( \begin{align} Sum = \frac{(a_l+a_r)\times (l-r+1)}{2} \end{align} \)​
这个就不给予推导过程，因为基本人人都会，属于小学必学知识。

求中项

我们先给出一个定义，若 \(a\)，\(b\)，\(c\) 三个数按这个顺序排列成等差数列，那么 \(b\) 叫 \(a\) ，\(c\) 的等差中项，而 \(a\)，\(b\)，\(c\) 成等差数列的充分必要条件是\(b=\frac{a+c}{2}\)​，这一公式也称之为等差数列中项公式。

等差数列公式也可以表示为： \(a_n = \frac{a_{n-1}+a_{n+1}}{2}\)。

这就是说，在一个等差数列中，从第\(2\)项起，每一项（有穷等差数列的末项除外）都是它的前一项与后一项的等差中项。

我们给出一道例题：

我们在 \(2\) 和 \(6\) 之间插入一个数 \(A\) ，可以使{2,A,6}构成一个等差数列，请求这个数 \(A\)。

我们可以很轻松的求出：

\( \begin{align} A= \frac{2+6}{2} = 4 \end{align} \)​

等比数列

定义

等比数列是指从第二项起，每一项与它的前一项的比值等于同一个常数的一种数列，这个常数叫做公比，注意等比数列首项不能为零，公比也不能为零，递推公式可表示为 \(a_n = a_{n-1} r\)。

等比数列一般形式为：{\(a\)，\(ar\)，\(ar^2\)，\(ar^3\)，\(ar^4\)…}

其中 \(a\) 是首项，\(r\) 是项与项之间的比，即公比。

通项公式

求通项公式时，我们就可以观察一下，发现等比数列每一项都由两个部分组成，即每一项都是第一项的值与一个常数的次方的积组成，即可以表示为 \(a_1\) 与 \(r^k (k\in N^{*})\) 的乘积，经观察得出，\(k\) 与 \(n\) 的关系是 \(k=n-1\) ，所以通项公式便是：\(a_n=a_1r^{n-1}\)

计算公式

求和

若一个等比数列 {\(a_n\)} 的首项为 \(a_1\) ，公比为 \(r\)，则有：
\( \sum_{k=0}^{n-1}{(ar^k)}=\left\{ \begin{aligned} & na_1(r=1)\\ & a_1\left( \frac{1-r^n}{1-r} \right)(r \ne 1) \end{aligned} \right. \)

我们来推导一下，

若一个等比数列 {\(a_n\)} 公比 \(r\) 为 \(1\) ，则会发现该数组为{a,a,a,a…} ，即所有项都相等且都等于首项，所以求和公式为：\(S_{a_n} = na_1\)。

而当 \(r \ne 1\) 时，我们仍然利用类似于等差数列求和推导方法：

首先，我们设数列的和为 \(S\)，则 \(S = a + ar+ar^2+…+ar^{n-2}+ar^{n-1}\)

接下来，将 \(S\) 乘 \(r\)：\(Sr = ar+ar^2+ar^3+…+ar^{n-1}+ar^{n}\)​。

你或许会注意到，\(S\) 和 \(Sr\) 很像，于是将他们相减：

	\(S\)	\(=\)	\(a\)	$+ $	\(ar\)	\(+\)	\(ar^2\)	\(+\)	…	\(+\)	\(ar^{n-1}\)
$ -$	\(Sr\)	\(=\)		$- $	\(ar\)	$- $	\(ar^2\)	\(-\)	…	\(-\)	\(ar^{n-1}\)	$- $	\(ar^n\)
	\(S-Sr\)	\(=\)	\(a\)	\(+\)	\(0\)	+	\(0\)	\(+\)	…	\(+\)	\(0\)	\(-\)	\(ar^n\)

会发现最后中间的项全部互相抵消。

所以对最后减去的结果变形：

\( \begin{align} S-Sr &= a-ar^n \\ S(1-r) &= a(1-r^n) \\ S & = a \left( \frac{1-r^n}{1-r}\right) \end{align} \)​

这便是我们要推导的公式了。

求级数

当且仅当在无穷等比数列中，此时 \(n\) 不断趋近于 \(+\infty\) ，所以若当 \(r < 1\) 时，\(r^n\) 便逐渐趋近于 \(0\)，这很好理解，当一个数乘一个小于 \(1\) 的数时便会缩小，例如 \(10 \times 0.1 = 1 < 10\)，所以乘无穷个的话，就会趋近于零，此时求级数公式便是：

\( \begin{align} \sum_{k=0}^{\infty}{(ar^k)} = a\left( \frac{1}{1-r}\right) \end{align} \)

实际应用

要利用等比公式，这里有一个非常经典的论题，即 \(0.\dot{9}\) 是否等于 \(1\)。

我们可以来证明一下，看这一个等比数列 {\(a_n\)} 为{0.9,0.09,0.009…}。

我们可以发现，这个数列首项 \(a_1\) 为 \(0.9\) ，公比 \(r\) 为 \(0.1\)（即每次缩小十倍）。

同时我们也惊奇的发现，这一无穷数列的级数便为 \(0.\dot{9}\)，这很好理解。

但若我们利用等比数列求级数公式进行计算：

\( \begin{align} \sum_{k=0}^{\infty}{\left(0.9\times 0.1^k \right)} & = 0.9\left(\frac{1}{1-0.1}\right) \\ & = 0.9\left(\frac{1}{0.9}\right) & = 1 \end{align} \)

可见， \(0.\dot{9}\) 确实等于 \(1\)。

斐波那契数列

注意这是本文章之重点，也是写本文章之初衷（请回顾前言）。

定义

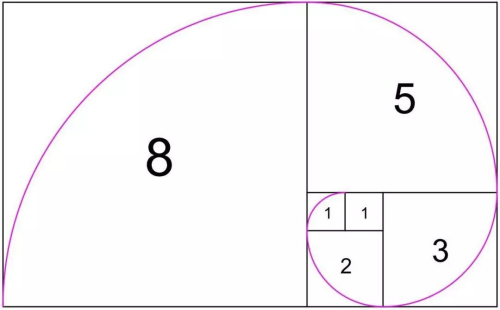
斐波那契数列就是这一数列：{0,1,1,2,3,5,8…}

即为下一项为上两项的和，注意，只有这一数列是斐波那契数列，满足该规律但不是这一数列的，只能称之为类斐波那契数列。

按照这些数为边长画正方形，便可以得到斐波那契矩形：

故斐波那契数列数列之别名之一又叫做黄金分割数列。

同时，数学家斐波那契是运用兔子繁殖来引入该数列的，便也可以叫做兔子数列。

我们来介绍一下这一问题：假定一对大兔子每月能生一对小兔子，且每对新生的小兔子经过一个月可以长成一对大兔子，具备繁殖能力，如果不发生死亡，且每次均生下一雌一雄，一开始有一对小兔子，问一年后共有多少对兔子？

我们可以通过列表来解决：

时间（月）	0	1	2	3	4	5	6	7	8	9	10	11	12
幼兔（对）	1	0	1	1	2	3	5	8	13	21	34	55	89
成兔（对）	0	1	1	2	3	5	8	13	21	34	55	89	144
总兔（对）	1	1	2	3	5	8	13	21	34	55	89	144	233

注意看，总兔的对数是不是就是我们熟知的斐波那契数列？

我们再给出一个数学函数定义，也可看作其递推公式：

\( Fib(n)=\left\{ \begin{aligned} & 0 \left(n = 0\right)\\ & 1 \left(n = 1\right)\\ & Fib(n-2)+Fib(n-1) \left(n > 1\right) \end{aligned} \right. \)

通项公式推导

斐波那契数列的通项公式在前文就已经提到过了，我们再来认识一下。

\(\begin{align} {a_n =\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^{n}-\left(\frac{1-\sqrt{5}}{2}\right)^{n}\right]} \end{align}\)

虽然他看起来很麻烦，但是我们还是得证明一下，注意，博主确实只是一个初三学生，没有能力自己推导，只能借鉴他人思路，希望原作者理解（但绝不是照搬）。

我们先从递推公式入手吧：
\( \begin{align} F(n) = F(n-1) + F(n-2) \end{align} \)

它也可以看作：
\( \begin{align} F(n) = aF(n-1) + bF(n-2) \end{align} \)

可以确定的是，当 \(a = b = 1\) 的时候，就是斐波那契数列，那我们就可以先求出这个式子的通项公式。

1. 先将等式两边同时加上 \(xF(n-1)\)

   \( \begin{align} F(n) + xF(n-1) & = aF(n-1) + bF(n-2) + xF(n-1) \\ & = (a+x)F(n-1) + bF(n-2) \\ & = (a+x)F(n-1) + (a+x)\frac{b}{a+x}F(n-2)\\ & = (a + x)\left[ F(n-1) + \frac{b}{a+x}F(n-2)\right] \end{align} \)

2. 我们再引申出一个新的数列，\(G(n) = F(n)+xF(n-1)\)，我们发现必然能够找到一个常量 \(x\)， 使得这一新数列是一个等比数列，且公比为 \(a + x\)，则有（说实话，这步博主自己推完都难以理解）
   先有新数列得出以下两式：
   \( \begin{align} G(n) = F(n)+xF(n-1) \end{align} \)
   \( \begin{align} G(n-1) = F(n-1) + xF(n-2) \end{align} \)
   又因为等比数列的后一项等于前一项乘公比得出下面式子：
   \( \begin{align} G(n) & =G(n-1) \times (a+x)\\ & = (a+x)(F(n-1)+xF(n-2)) \end{align} \)
   再结合之前的推出：
   \( \begin{align} G(n) = F(n)+xF(n-1) = (a + x)\left[ F(n-1) + \frac{b}{a+x}F(n-2)\right] \end{align} \)
   最后联立方程：
   \( \begin{align} (a + x)\left[ F(n-1) + \frac{b}{a+x}F(n-2)\right] &= (a+x)(F(n-1)+xF(n-2)) \\ \frac{b}{a+x} &= x \\ x^2 + ax - b &= 0 \end{align} \)

   带入求根公式求根：
   \( \begin{align} x_1 &= \frac{-a-\sqrt{a^2+4b}}{2} \\ x_2 &= \frac{-a+\sqrt{a^2+4b}}{2} \end{align} \)

   当\(a = b = 1\) 的时候就分别等于：
   \( \begin{align} x_1 &= \frac{ - 1 - \sqrt{5}}{2} \\ x_2 &= \frac{- 1 + \sqrt{5}}{2} \end{align} \)

3. 根据等比数列的前项和后项的关系\(\frac{a_n}{a_{n-1}}=r\)​：

   令公比 \(r = a+x\) 即可知：
   \( \begin{align} \frac{F(n)+xF(n-1)}{F(n-1)+xF(n-2)} = r \end{align} \)

4. 累乘起来：
   \( \begin{align} \frac{F(n)+xF(n-1)}{F(n-1)+xF(n-2)} \times \frac{F(n-1)+xF(n-2)}{F(n-2)+xF(n-3)} \times …\times \frac{F(2)+xF(1)}{F(1)+xF(0)} \\ = \frac{F(n)+xF(n-1)}{F(1)+xF(0)} = r^{n-1} \end{align} \)

5. 再令 \(p = F(1) + xF(0)\)得出：
   \( \begin{align} F(n) + xF(n-1) = r^{n-1}(F(1)+xF(0)) = r^{n-1}p \end{align} \)

6. 再通过上面的方法，引入一个变量 \(y\) ，使得 \(F(n)+yr^n\) 是一个公比为 \(-x\) 的等比数列，等式两边同时加上 \(yr^n\)：

   \( \begin{align} F(n) + xF(n-1) & = r^{n-1}(F(1)+xF(0)) = r^{n-1}p \\ F(n) & = -xF(n-1) + r^{n-1}p \\ F(n) + yr^n & = -xF(n-1) + r^{n-1}p+yr^n \\ F(n) + yr^n & = -x \left[ F(n-1) + \frac{r^{n-1}p+yr^n}{-x} \right] \end{align} \)

7. 于是便得出
   \( \begin{align} yr^{n-1} = \frac{r^{n-1}p+yr^n}{-x} \end{align} \)
   同样累乘起来：
   \( \begin{align} \frac{F(n)+yr^n}{F(n-1)+yr^{n-1}} \times …\times \frac{F(1)+yr}{F(0)+y} = \frac{F(n)+yr^n}{F(0)+y} = (-x)^n \end{align} \)

8. 我们计算一下 \(y\) 的值，等式两边同时除去 \(r^{n-1}\) 得到：
   \( \begin{align} y & = \frac{p+yr}{-x} \\ & = - \frac{p}{x + r} \\ & = - \frac{ F(1) + xF(0)}{2x + a} \end{align} \)

9. 最后化简累乘的结果，再带入所有算完的值进行求解就能得到：
   \( \begin{align} F(n) & = (-x)^n \times (F(0)+y)-yr^n \\ & = (-x)^n \frac{2x+1-x-1}{2x+1}+\frac{x+1}{2x+1}(x+1)^n \\ & = \frac{(x+1)^{n+1} - x^{n+1}}{2x+1} \\ \end{align} \)
   \( \begin{align} {F(n) =\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^{n}-\left(\frac{1-\sqrt{5}}{2}\right)^{n}\right]} \end{align} \)

完结撒花~

后言

这篇文章对于一个即将面临中考的初三学生来说，绝对可以称得上鸿篇巨制了，总码字量达到了一万三千字符左右，历时 \(8\) 天，每天平均工作时长可达 \(5\) 个小时，查阅资料近 \(20\) 篇，其中不乏有一些文章推导过程对于初中生来说太过简略，需要自己重新推导，可谓呕心沥血之作，希望可以帮到大家。