[整理]字符串全家桶之从普及组到切黑题(零基础最友好向)
字符串串恶心心
0.前言
本篇博客创作初衷是对于一些看起来没那么简单、显然的算法(例如哈希算法,虽然应用也很多,但基本原理是很浅显的,故没有放在本篇博客中)做一些尽量让新人看得懂、理解得清楚的讲解。本篇博客会尽量使用浅显易懂、生动形象的语言来诠释某个算法或数据结构,同时穿插代码以便于理解;有些较易的证明或较显然的性质在文中略去,也是由于希望读者能够积极思考的缘故。由于作者就是一个对于字符串算法理解得尤其不清楚的人,所以写下这篇博客花费了作者不少心血去重新学习、理解一些算法,如果它对在学某个算法却一直理解不清楚的你起到了一丝微薄的帮助,那么请给作者点赞支持吧!
内容主要按照知识点相关性排列,难度不一定递增,标题前加 * 的为拓展内容,建议在第一遍阅读时略读或跳过。
由于个人整理,知识点难免有不全、缺漏之处,如果您发现了作者遗漏了某些算法,或是对于某些算法的讲解不够深入,希望能在评论区留下您的意见和建议。
1.KMP、*扩展 KMP、Trie 和 AC 自动机
难度:普及~省选
1.0 KMP
既然题目这么说了,那么我们当然要从普及组难度的讲起。
KMP 用于求解单模式匹配问题。
为什么暴力不可行,是因为它没有吸取之前的教训,由于从一个位置失配意味着这个位置之前的全部匹配,所以我们可以根据这个跳过那些不可能的位置。
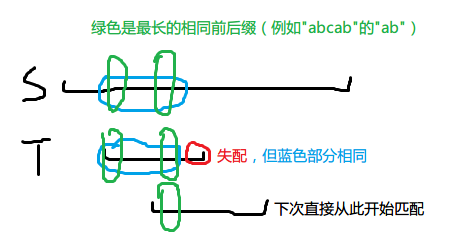
我们发现这个绿色部分(以下记作 \(\text{nxt}\) 数组)非常强,那么如何求它呢?
考虑如何递推出它,发现它有美妙的性质:
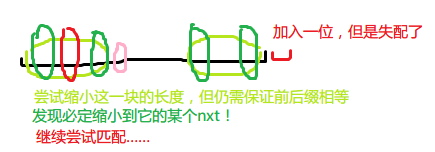
不难分析出这个过程是 \(\mathcal O(n)\) 的。
模板题核心代码如下(由于年代久远码风与现在有较大的不同):
int len1,len2,j,nxt[1000010];
char s1[1000010],s2[1000010];
int main(){
cin>>s1+1>>s2+1;
len1=strlen(s1+1),len2=strlen(s2+1);
for(int i=2;i<=len2;i++){
while(j&&s2[i]!=s2[j+1])j=nxt[j];
if(s2[j+1]==s2[i])j++;
nxt[i]=j;
}
j=0;
for(int i=1;i<=len1;i++){
while(j>0&&s2[j+1]!=s1[i])j=nxt[j];
if(s2[j+1]==s1[i])j++;
if(j==len2){
cout<<i-len2+1<<endl;
j=nxt[j];
}
}
for(int i=1;i<=len2;i++)cout<<nxt[i]<<" ";
return 0;
}
1.1 Trie
Trie 是一个很好理解的数据结构,它是对多个字符串信息的一种压缩。
一张图就可以讲明 Trie 树的结构,对 "he","her","his","him","dark","dash" 构建的 Trie 树长这样:

其中节点的编号没有意义,边表示字符,从根节点向下走,遇到结束标记(图中加粗的节点)就代表有一个字符串结束。
容易发现它的节点数为 \(\mathcal O(n|s|)\)(其中 \(n\) 为字符串个数,\(|s|\) 为字符串长度)。
1.2 AC 自动机
AC 自动机(Aho-Corasick Automaton,顾名思义是あほ算法),可简称 ACAM,是在 Trie 树上运用 KMP 的思想进行多模式匹配。
先来介绍自动机的概念。自动机是一个数学模型,我们在 OI 中基本上接触的是确定性有限状态自动机(DFA)。
一个自动机由字符集、状态集合、起始状态、接受状态集合和转移函数构成,它可以看做一张 DAG,状态相当于图上的节点,而转移函数相当于有向边。
输入一个字符串,按照转移函数一个一个字符地转移,如果最终到达的是接受状态则接受这个字符串,反之不接受。
例:我们刚刚讲的 Trie 是一个自动机,它接受且仅接受指定的字符串集合。
回到 ACAM。它有一个关键的概念叫做 \(\text{fail}\) 指针,实际上和 KMP 中的 \(\text{nxt}\) 数组定义差不多:它指到当前状态的最长后缀。
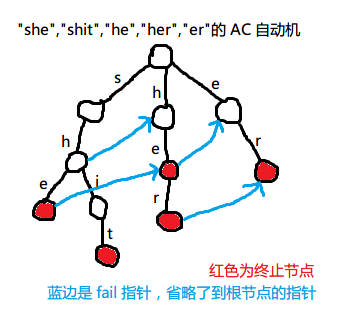
加入一个字符时的求解过程和 KMP 是类似的:沿着父节点的 \(\text{fail}\) 指针向上,直到跳到的节点拥有该字符的儿子,连向这个儿子。
但是一次次跳 \(\text{fail}\) 指针太慢了,我们可以 BFS 来优化这个过程。
简单版核心代码如下(同样是年代久远的代码):
int tot;
struct Node{
int fail,ed,son[26];
}tr[1000010];
il void Insert(string s){//建Trie树
int len=s.length(),now=0,tmp;
for(rg int i=0;i<len;i++){
tmp=s[i]-'a';
if(!tr[now].son[tmp])tr[now].son[tmp]=++tot;
now=tr[now].son[tmp];
}
tr[now].ed++;
}
il void Fail(){//求失配指针
queue<int> q;
for(rg int i=0;i<26;i++){//第二层都指向根节点,先处理出来
if(tr[0].son[i]){
tr[tr[0].son[i]].fail=0;
q.push(tr[0].son[i]);
}
}
while(!q.empty()){
int now=q.front();q.pop();
for(rg int i=0;i<26;i++){
if(tr[now].son[i]){//跳父亲的fail
tr[tr[now].son[i]].fail=tr[tr[now].fail].son[i];
q.push(tr[now].son[i]);
}else tr[now].son[i]=tr[tr[now].fail].son[i];
}
}
}
il int Find(string s){//匹配
int len=s.length(),now=0,tmp,ans=0;
for(rg int i=0;i<len;i++){
tmp=s[i]-'a',now=tr[now].son[tmp];
for(rg int j=now;j&&tr[j].ed!=-1;j=tr[j].fail){
ans+=tr[j].ed,tr[j].ed=-1;
}
}
return ans;
}
*1.3 扩展 KMP
扩展 KMP 又称为 Z 算法,它的核心是 Z 函数:对于一个字符串 \(s\),\(z(i)\) 表示 \(s\) 与 \(s[i,n]\) 的最长公共前缀长度,下面我们可以看到,它是可以 \(\mathcal O(n)\) 计算的。
我们依然去递推这个东西,其实这里的递推方式(大部分直接转移、小部分均摊线性暴力)很像 4.0 中要讲的 Manacher 算法,如果不理解接下来的递推方式不妨先看看那部分,再将它们放到一起对比学习。
对于一个 \(i\) 我们称区间 \([i,i+z(i)-1]\) 为 \(i\) 的匹配段或 Z-box,计算的时候我们需要维护右端点最靠右的 Z-box(设为 \([l,r]\)),这样我们就可以分情况讨论 \(i\) 与 \(r\) 的关系(如下图)。
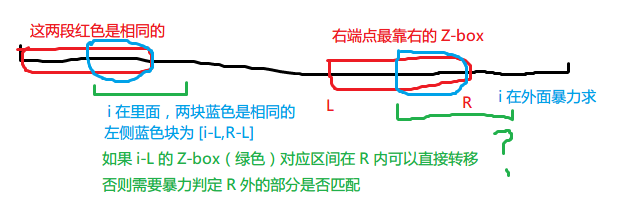
两个字符串匹配是大同小异的(这一点和 KMP 相似)。
模板题核心代码:
const int N=20000010;
int n,m,z[N],lcp[N];
LL ans;char s[N],t[N];
signed main(){
scanf("%s%s",s+1,t+1),n=strlen(s+1),m=strlen(t+1);
z[1]=m,ans=m+1;
for(rg int i=2,l=0,r=0;i<=m;i++){
if(i<=r)z[i]=min(z[i-l+1],r-i+1);
while(i+z[i]<=m&&t[i+z[i]]==t[z[i]+1])z[i]++;
if(i+z[i]-1>r)l=i,r=i+z[i]-1;
ans^=(LL)i*(z[i]+1);
}
cout<<ans<<endl,ans=0;
for(rg int i=1;i<=min(n,m);i++,lcp[1]++){
if(s[i]!=t[i])break;
}ans=lcp[1]+1;
for(rg int i=2,l=0,r=0;i<=n;i++){//与上面是几乎相同的,甚至可以封装到一个函数里,不过我这里懒就没封
if(i<=r)lcp[i]=min(z[i-l+1],r-i+1);
while(i+lcp[i]<=n&&s[i+lcp[i]]==t[lcp[i]+1])lcp[i]++;
if(i+lcp[i]-1>r)l=i,r=i+lcp[i]-1;
ans^=(LL)i*(lcp[i]+1);
}
cout<<ans<<endl;
KafuuChino HotoKokoa
}
while 循环一定会导致 \(r\) 增加,所以均摊下来是 \(\mathcal O(n)\) 的。
1.4 应用
例题 \(1.0\):[NOI2014]动物园
这个题的答案限制太多了,我们先考虑求一个没有长度限制的 \(\text{num}\)。有一个暴力的想法就是直接跳 \(\text{nxt}\) 数组看跳了多少次,不过我们发现可以在递推 \(\text{nxt}\) 时顺便求出来,所以就解决了弱化版的问题。现在考虑加上这个一半长度限制怎么办,我们发现一个等价的做法就是每次暴力跳 \(\text{nxt}\) 直到长度小于一半。
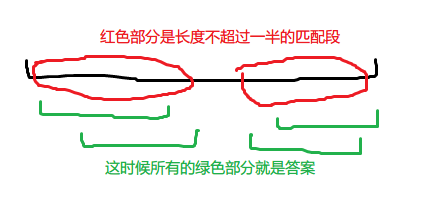
计算答案那部分的核心代码:
for(rg int i=2,j=0;i<=n;i++){
while(j&&s[i]!=s[j+1])j=nxt[j];
if(s[i]==s[j+1])j++;
while((j<<1)>i)j=nxt[j];
ans=(LL)ans*(num[j]+1)%p;
}
在实际应用中,以上几种算法一般不会单独使用,而是作为 dp 等算法的辅助工具。
例题 \(1.1\):[JSOI2007]文本生成器
在 OI 中我们经常会遇到 ACAM 上 dp 的问题,它有一个常见套路就是设 \(f_{i,j}\) 为第 \(i\) 个点、第 \(j\) 个字符的答案,然后再带一些附加信息便于转移。这道题中我们要求至少经过一个结束标记,于是可以设 \(f_{i,j,0/1}\) 表示第 \(i\) 个点、第 \(j\) 个字符、没有/有经过结束标记的方案数。那么答案就是 \(\sum f_{u,m,1}\),转移需要从父亲转移到儿子,再特判到达一个结束标记的情况,时间复杂度大概是 \(\mathcal O(nm^2|\Sigma|)\)?。
需要注意特殊处理后缀关系,建自动机时如果一个点的 \(\text{fail}\) 指针指向的点有结束标记,那么这个串也需要打标记。
例题 \(1.2\):[BJOI2019]奥术神杖
我们发现这个答案式子实在是太难受了,尝试通过取对数把它转化成加法:\(\dfrac1c\sum\ln v_i\),然后这东西可以二分,答案可行等价于 \(\sum(\ln v_i-mid)>0\),然后在自动机上 dp,需要注意 dp 时记录决策点以便输出方案。
2.后缀数组和后缀自动机
难度:省选~NOI
2.0 后缀数组简介
对于一个字符串,将它的所有后缀排序得到一个 \(\text{sa}\) 数组表示排名对应的后缀,\(\text{rk}\) 数组表示后缀的排名,这两个数组是互逆的。
我们还可以通过 \(\text{sa}\) 得到另一个很有用的数组 \(\text{height}\),它表示排名相邻的两个后缀的最长公共前缀,求法也会在下面提到。
2.1 倍增
我们根据后缀的性质,可以倍增在 \(\mathcal O(n\log n)\) 的时间内求解。
考虑先排序第一个字符,再倍增排序的长度。只排一个字符是很简单的,但是加上第二个字符怎么排呢?我们需要重新排序一遍吗?
显然是不用的,假设我们已经排好了前 \(k\) 位想要排接下来的 \(k\) 位,我们发现第 \(i\) 个后缀的后 \(k\) 位就是第 \(i+k\) 个后缀的前 \(k\) 位。
所以说我们可以用第 \(i\) 个后缀前 \(k\) 位作为第一关键字,第 \(i+k\) 个后缀前 \(k\) 位作为第二关键字进行排序,这样就完成了一次倍增。
最终的复杂度是倍增的 \(\mathcal O(\log n)\) 乘上排序的 \(\mathcal O(n\log n)\),如果使用基数排序(没接触过的读者可以自行查找资料学习)可以优化到 \(\mathcal O(n\log n)\)。
下面对于倍增法的代码进行重点讲解,这里也是很多人容易记不住或理解不了的部分,在代码中给出了较为详细的注释。
const int N=200010;
int n;char s[N];
int m,sa[N],rk[N],c[N],y[N];
//sa和rk与上文一致,c是基数排序用到的桶,y用于临时存储第二关键字
il void Sort(){//这个函数实现的是双关键字基数排序,rk为第一关键字,y为第二关键字
for(rg int i=1;i<=m;i++)c[i]=0;
for(rg int i=1;i<=n;i++)c[rk[i]]++;
for(rg int i=2;i<=m;i++)c[i]+=c[i-1];
for(rg int i=n;i;i--)sa[c[rk[y[i]]]--]=y[i];
//如果不理解这里请自行查阅资料
}
il void SA(){
for(rg int i=1;i<=n;i++)rk[i]=s[i],y[i]=i;//先只排第一个字符
Sort();
for(rg int k=1;k<=n;k<<=1){//倍增,k意同上文
int num=0;
for(rg int i=n-k+1;i<=n;i++)y[++num]=i;
for(rg int i=1;i<=n;i++)if(sa[i]>k)y[++num]=sa[i]-k;
//以上两行是一个优化:先把第二关键字为空的放进去,再放剩下的
Sort(),swap(rk,y);//备份rk作为下次的第二关键字
rk[sa[1]]=num=1;
for(rg int i=2;i<=n;i++){
//两个关键字均相同或有不相同
if(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k]){
rk[sa[i]]=num;
}else rk[sa[i]]=++num;
}
if(num==n)break;//已经能够区分所有后缀
m=num;
}
}
*2.2 SA-IS
想学线性求 SA 的算法,但由于看不懂 DC3 的论文,又听说 SA-IS 跑得像香港记者,所以就抛弃 DC3 投入 SA-IS 的怀抱了。
我们首先会在字符串结尾加入一个哨兵节点 \(\texttt{#}\),然后再对于每个后缀进行分类:一个后缀是 S 型或 L 型当且仅当它小于或大于它的下一个后缀,一个字符的类型是它对应的后缀的类型。特别地,我们认为后缀 \(\texttt{#}\) 是 S 型的。
例如字符串 \(\texttt{abbccbabb#}\) 的每个后缀的类型就是 \(\texttt{SSSLLLSLLS}\)。
容易发现 \(s[i]<s[i+1]\) 或 \(s[i]>s[i+1]\) 时 \(s[i\dots n]\) 必然是 S 型或 L 型,否则直接继承 \(s[i+1\dots n]\) 的类型即可,于是我们可以线性递推出每个后缀的类型(记作 \(t\) 数组)。
下面我们有 LMS 字符和 LMS 子串的概念:LMS 字符是左边为 L 型的 S 型字符(或者说是一段 S 型字符中最靠左的一个),LMS 子串是 LMS 字符分割出的串(包含两端的 LMS 字符本身),将 LMS 子串出现的位置记作 \(p\) 数组。
我们想要对 LMS 子串进行排序,就要定义比较方式:在比较字典序的基础上,比较每个字符的类型,因为两个字符相同时显然 S 型的更大。
现在我们把所有 LMS 子串排序、离散化得到一个 \(s_1\) 数组。

如图,\(\texttt{*}\) 标记的是 LMS 字符,右侧是桶排序的结果。
然后我们惊奇地发现,这个 \(s_1\) 有一个保序性:\(s_1\) 中相邻后缀的大小关系等价于原串中对应位置后缀的大小关系!
由于 LMS 子串至少间隔一个字符,所以 \(s_1\) 的长度会减半,我们就缩小了问题规模。现在假设我们已经求出了 \(s_1\) 的后缀数组 \(\text{sa}_1\),考虑如何求出原串的后缀数组 \(\text{sa}\)。
考察 SA 的结构:由于它将后缀排好了序,所以首字母相同的后缀一定是一个连续段,而且这一段内部的 S 型后缀和 L 型后缀也是分别连续的(由于 L 型后缀小于 S 型后缀,所以 L 型后缀集中在前面),我们可以把这些连续段看成一个个桶。
那么现在我们有了一个从 \(\text{sa}_1\) 导到 \(\text{sa}\) 的方法:
- 确定 S 桶的起始位置。把 \(\text{sa}_1\) 中的所有后缀加入对应位置的 S 桶中;
- 确定 L 桶的起始位置。从左往右扫一遍 \(\text{sa}\),如果 \(s[\text{sa}[i]-1]\) 为 L 型则将 \(\text{sa}[i]-1\) 从右侧加入 L 桶中;
- 重新确定 S 桶的起始位置。从右往左扫一遍 \(\text{sa}\),如果 \(s[\text{sa}[i]-1]\) 为 S 型则将 \(\text{sa}[i]-1\) 从左侧加入 S 桶中。
简要证明一下这样做的正确性。第一步由于排出来的不是最终结果所以无需证明,只需要知道它将已经排好序的 LMS 子串按顺序加入了新的数组。对于第二步,由于后缀 \(i\) 只会被后缀 \(i-1\) 导入,而后缀 \(i-1\) 是 L 型后缀,所以由大小关系易知每个 L 型后缀都会被加入;又因为 \(s[i-1\dots n]>s[i\dots n]\) 且 \(s[i\dots n]\) 先被导入,所以导入的 L 后缀一定是排好序的。对于第三步,证明与第二步类似。
现在我们已经几乎得到了 SA-IS 算法了,唯一的问题是如何快速排序 LMS 子串。我们当然可以写一个很麻烦的东西来完成它(事实上,这就是另一个线性算法 KA 的流程。但是举个例子,对字符串进行基数排序的代码复杂度是可想而知的……),但是 SA-IS 告诉我们,这一步也可以用诱导排序完成。
实现也很简单,只需将第一步改为将 LMS 字符放入桶中即可。为了证明它的正确性,下面引入 LMS 前缀的概念:LMS 前缀是从当前字符到第一个位置大于等于它的 LMS 字符这一段构成的子串,容易发现 LMS 字符的 LMS 前缀是它本身,LMS 前缀的类型是开头字符的类型。
对于第一步,放入后一定是有序的。对于第二、第三步,只需要数学归纳然后反证即可。
由于每次都是 \(\mathcal O(|s|)\) 的,而每次 \(s\) 的长度减半,所以总复杂度为 \(\mathcal O(|s|)\)。
看了上面的过程可能会觉得很混乱,所以下面给出模板题核心代码便于理解(坑点只是卡了我的地方,可能对读者没有什么杀伤力):
const int N=2000010;
int n,s[N];bool t[N];//0:L型 1:S型
int sa[N],rk[N],p[N],b[N],c[N];
//加入L/S桶
#define L(x) sa[c[s[x]]++]=x
#define S(x) sa[c[s[x]]--]=x
//诱导排序,需要先加入LMS后缀
//坑点:注意传入s的头指针
il void IS(int *sa,int *s,bool *t,int *b,int n,int m){
//此处c数组作为L桶左端点,需要注意边界
for(rg int i=1;i<=m;i++)c[i]=b[i-1]+1;
//坑点:sa[i]>1
for(rg int i=1;i<=n;i++)if(sa[i]>1&&!t[sa[i]-1])L(sa[i]-1);
//此处c数组作为S桶右端点
for(rg int i=1;i<=m;i++)c[i]=b[i];
for(rg int i=n;i;i--)if(sa[i]>1&&t[sa[i]-1])S(sa[i]-1);
}
//主体过程
void SAIS(int *s,bool *t,int *p,int *b,int n,int m){
//#为S型
t[n]=1;int tot=0,num=1,*s1=s+n+1;fill(rk+2,rk+1+n,0);
//分类
for(rg int i=n-1;i;i--)t[i]=s[i]==s[i+1]?t[i+1]:s[i]<s[i+1];
//记录LMS字符
for(rg int i=2;i<=n;i++)if(t[i]&&!t[i-1])p[rk[i]=++tot]=i;
//fill可换成memset,此处仅作卡常
fill(sa+1,sa+n+1,0);
for(rg int i=1;i<=n;i++)b[s[i]]++;
for(rg int i=1;i<=m;i++)b[i]+=b[i-1];
//此处c数组作为S桶右端点
for(rg int i=1;i<=m;i++)c[i]=b[i];
//加入所有LMS字符,进行第一轮排序
for(rg int i=tot;i;i--)S(p[i]);
IS(sa,s,t,b,n,m);
//离散化新数组
for(rg int i=1,x=0,lst=0;i<=n;i++){
if(x=rk[sa[i]]){
for(rg int j=p[x],k=p[lst];j<=p[x+1];j++,k++){
if(s[j]^s[k]){
num++;break;
}
}
s1[lst=x]=num;
}
}
//是否各不相同
if(num<tot)SAIS(s1,t+n+1,p+tot+1,b+m+1,tot,num);
else for(rg int i=1;i<=tot;i++)sa[s1[i]]=i;
//同上,先加入LMS后缀
for(rg int i=1;i<=tot;i++)s1[i]=p[sa[i]];
for(rg int i=1;i<=m;i++)c[i]=b[i];
fill(sa+1,sa+n+1,0);
for(rg int i=tot;i;i--)S(s1[i]);
IS(sa,s,t,b,n,m);
}
原论文中提到它可以用约 \(100\) 行来实现,可以看出只要压行压得好这个数字是很宽松的,我实现时(不带注释)用了约 \(40\) 行,仅比倍增法多了十几行。但很遗憾的是,根据洛谷和 UOJ 的评测结果来看,由于常数巨大它比我的倍增法快不了多少
2.3 后缀自动机简介与构造方法
后缀自动机(SAM)可以理解成一个将原字符串所有后缀的信息高度压缩的一个图,后面会提到它的点数和边数仅为 \(\mathcal O(n)\)。
SAM 与 SA 并没有什么关系,甚至比 SA 简单不少(指模板题难度和代码复杂度),如果你不能理解 SA 也请继续往下看(然后发现更加理解不了 SAM)。
先来介绍几个概念。
定义一个字符串的 \(\text{endpos}\) 为它在原串中的所有结束位置。例如对于字符串 \(\texttt{abcabcc}\),\(\text{endpos}(\texttt{abc})=\{3,6\},\text{endpos}(\texttt{c})=\{3,6,7\}\)。
显然 \(\text{endpos}\) 的包含关系代表了字符串的后缀关系,而不包含的 \(\text{endpos}\) 集合一定不交。
然后我们发现 \(\text{endpos}\) 集合的包含关系(称为后缀链接 \(\text{fa}\))构成了一棵树(称为后缀链接树或 Parent 树),每个点的父亲是它最长的 \(\text{endpos}\) 集合与该点不同的后缀。
我们还有一个 \(\text{len}\) 用于表示该点对应的最长字符串长度。
接下来考虑如何构建 SAM,我们增量构造,考虑插入一个新字符 \(c\) 时会发生什么。
首先整个串由于长度加了一肯定要作为一个新的状态和上一个状态连边的,然后我们需要看其他后缀怎么转移过来。
我们先沿着上一次的状态在 Parent 树上向上跳,每次都加入一个到 \(c\) 的转移,直到这个点已经存在 \(c\) 的转移(设这个点为 \(p\))。
如果 \(p\) 没有跳到根,那么说明我们找到了一个转移 \(p\xrightarrow{c}q\),也就是我们找到了一个 \(s\) 的后缀 \(x\) 满足 \(x+c\) 在 \(s\) 中出现过。
如果这个转移满足 \(\text{len}(p)+1=\text{len}(q)\),意味着 \(q\) 对应的最长串就是 \(x+c\),去掉 \(c\) 之后得到的 \(x\) 一定包含了前面的所有后缀。
否则情况就有亿些麻烦了,由于 \(c\) 的后缀链接必须连到最大长度为 \(\text{len}(p)+1\) 的状态上而 \(q\) 对应了一个比 \(x+c\) 长的状态,所以需要分出来一个 \(q'\),让 \(\text{len}(q')=\text{len}(p)+1\)。也就是说,原来的 \(q\) 对应的某些 \(y+c\) 的 \(y\) 不是 \(s\) 的后缀,我们需要把长度比较大的拿出来,在 \(q'\) 中保存更短的后缀 \(x+c\)。
那么怎么处理这个新点的转移和后缀链接呢?根据刚刚的分析,我们应该把 \(q\) 和 \(c\) 的后缀链接都变为 \(q'\),然后沿着 \(p\) 的后缀链接上跳,这时那些原本连向 \(q\) 的都不能转移了,应该先连到 \(q'\) 上。
这样,我们就完成了 SAM 的构造。
我们来整理一下算法的过程(起始节点为 \(1\)):
可能嵌套得有些迷惑,请仔细阅读。
正确性基本上已经顺带证了,它的空间复杂度(状态数和转移数)是线性的,那么时间均摊也是线性的。
*2.4 广义后缀自动机
普通的 SAM 可以解决一个字符串上的问题,而我们需要在多个字符串上解决同样的问题时就需要用到广义后缀自动机(GSAM),由于是多个串我们需要在 Trie 上建立(另说一句,GSAM 有很多假做法包括但不限于用特殊字符拼接、每个串分别插入 SAM 等等,它们通常能达到和 GSAM 一样的正确性,但是时间会有危险)。
我们在普通的 SAM 上有 \(\text{endpos}\)、后缀链接和 \(\text{len}\) 等概念,如何在 Trie 上体现这些呢?我们在普通 SAM 上插入的是一串 \(\text{len}\) 递增的节点,在 Trie 上我们把深度看成 \(\text{len}\) 的话就是按照 BFS 序在父亲上插入一串 \(\text{len}\) 不减的节点。
这里可能说得有些迷惑,其实它和刚刚假做法里的分别插入是差不多的,只不过借助 Trie 压缩了前缀使得复杂度正确。
它可以用于求解许多 SAM 能够求解的东西,例如多个字符串的本质不同子串数也是 \(\sum(\text{len}(u)-\text{len}(\text{fa}(u)))\)。
模板题核心代码如下,请注意 SAM 中变化的地方:
const int N=1000010;
int n;char s[N];
struct SAM {
struct Node {
int fa,len,ch[26];
}tr[N<<1];
int tot=1;
il int Extend(int c,int lst){
int p=lst,cur=++tot;
tr[cur].len=tr[p].len+1;
for(;p&&!tr[p].ch[c];p=tr[p].fa)tr[p].ch[c]=cur;
if(!p)tr[cur].fa=1;
else {
int q=tr[p].ch[c];
if(tr[q].len==tr[p].len+1)tr[cur].fa=q;
else {
int nq=++tot;tr[nq]=tr[q],tr[nq].len=tr[p].len+1;
tr[q].fa=tr[cur].fa=nq;
for(;p&&tr[p].ch[c]==q;p=tr[p].fa)tr[p].ch[c]=nq;
}
}
return cur;
}
il void Clear(){
for(rg int i=1;i<=tot;i++){
tr[i].fa=tr[i].len=0;
memset(tr[i].ch,0,sizeof(tr[i].ch));
}
tot=1;
}
}S;
struct Trie {
struct Node {
int ch[26],ed,c,fa;
}tr[N];
int tot=1,pos[N];
il void Insert(char *s){
int n=strlen(s+1),p=1;
for(rg int i=1;i<=n;i++){
if(!tr[p].ch[s[i]-97]){
tr[p].ch[s[i]-97]=++tot;
tr[tot].fa=p,tr[tot].c=s[i]-97;
}
p=tr[p].ch[s[i]-97];
}
tr[p].ed++;
}
il void BFS(){
queue<int> q;
for(rg int i=0;i<26;i++){
if(tr[1].ch[i])q.push(tr[1].ch[i]);
}
pos[1]=1;
while(!q.empty()){
int u=q.front();q.pop();
pos[u]=S.Extend(tr[u].c,pos[tr[u].fa]);
for(rg int i=0;i<26;i++){
if(tr[u].ch[i])q.push(tr[u].ch[i]);
}
}
}
}T;
int main(){
Read(n);
for(rg int i=1;i<=n;i++)scanf("%s",s+1),T.Insert(s);
T.BFS();LL ans=0;
for(rg int i=2;i<=S.tot;i++){
ans+=S.tr[i].len-S.tr[S.tr[i].fa].len;
}
cout<<ans<<endl;
KafuuChino HotoKokoa
}
另外,也可不显式构建 Trie,而是直接按照 Trie 的结构在线插入 SAM,具体来说,需要在前面分别插入的错误写法基础上加入两处特判。
我们需要特判什么呢?首先一个简单的特判是判断节点是否已经插入过,如果插入过直接返回。假做法里还有什么问题呢?
我们发现,假做法中的每次暴力插入会插出来一些奇奇怪怪的空节点,例如当有转移但 \(\text{len}(q)\ne\text{len}(p)+1\) 时,我们发现 \(\text{len}(cur)=\text{len}(p)+1\) 而它的最小长度为 \(\text{len}(q')+1=\text{len}(p)+2\),也就是说这个点没有储存任何一个串的信息,是一个空节点。空节点一般不会影响正确性,但是在某些题中可以构造数据卡掉它,故我们特判掉会产生空节点的情况。
il int Extend(int c,int lst){
int p=lst;
if(tr[p].ch[c]){
int q=tr[p].ch[c];
if(tr[q].len==tr[p].len+1)return q;//需要的节点已经插入过
else {//防止空节点,直接分裂
int nq=++tot;tr[nq]=tr[q],tr[nq].len=tr[p].len+1;
tr[q].fa=nq;
for(;p&&tr[p].ch[c]==q;p=tr[p].fa)tr[p].ch[c]=nq;
return nq;
}
}
int cur=++tot;
tr[cur].len=tr[p].len+1;
for(;p&&!tr[p].ch[c];p=tr[p].fa)tr[p].ch[c]=cur;
if(!p)tr[cur].fa=1;
else {
int q=tr[p].ch[c];
if(tr[q].len==tr[p].len+1)tr[cur].fa=q;
else {
int nq=++tot;tr[nq]=tr[q],tr[nq].len=tr[p].len+1;
tr[q].fa=tr[cur].fa=nq;
for(;p&&tr[p].ch[c]==q;p=tr[p].fa)tr[p].ch[c]=nq;
}
}
return cur;
}
由于不需要显式建 Trie,在线做法比离线做法快了一倍。
2.5 应用
2.5.0 SA 部分
很多题目用 SA 和 SAM 都可以做,所以接下来大概是先分别讲完两个东西的基础应用再混着讲一些题目。
然而由于 SAM 好写且功能强大所以大部分题采用了 SAM 做法
SA 的一个应用是求最小循环移位,例题 \(2.0\):[JSOI2007]字符加密。
对于循环移位的问题我们的常用套路是倍长原串,然后就可以直接进行后缀排序。
接下来我们重点讲解 \(\text{height}\) 数组的求法及用途。
首先根据 \(\text{height}\) 的定义我们容易发现 \(\text{height}(\text{rk}(i))\ge \text{height}(\text{rk}(i-1))-1\),然后我们根据这个性质暴力求解。
它可以求本质不同的子串个数,只需要用所有子串减去重复的 \(\text{height}\) 即可。
SA 还可以搭配并查集食用,例题 \(2.1\):[NOI2015]品酒大会。
由于 \(k\) 相似拥有很好的性质,所以我们从大到小枚举 \(\text{height}\),把一样的并查集合起来,记录集合中的最值和大小。
2.5.1 SAM 部分
关于 SAM,它死了很明显可以进行字符串匹配。
然后它还可以求本质不同的子串个数,由于每个子串都相当于自动机中的一些路径,所以不同子串的个数相当于起点开始的不同路径条数,这个可以 dp 计算。另外,还可以利用 Parent 树,每个点包含的子串数量是 \(\text{len}(u)-\text{len}(\text{fa}(u))\),它们的出现次数都是 \(\text{siz}(u)\)。
例题 \(2.2\):[SDOI2016]生成魔咒(子串计数)、例题 \(2.3\):[TJOI2019]甲苯先生和大中锋的字符串(出现次数)。类似地还可以计算不同子串的总长度。
SAM 还有一大应用是求两个串的最长公共子串。具体来说,假设现在要求 \(s\) 和 \(t\) 的最长公共子串,我们需要先建出 \(s\) 的 SAM,然后把 \(t\) 扔上去匹配。如果有当前字符的转移就转移下去,否则一直跳后缀链接跳到有这个转移为止,再找不到就只能重新开始一段了。
*2.5.2 GSAM 部分
其实上面也提到了,GSAM 的性质和 SAM 几乎一致,许多用 SAM 做的题可以原封不动搬到 GSAM 上做多串版本。与普通 SAM 不同的是,GSAM 的一个节点可能存储了多个串的信息无法分离,如果要求维护 \(\text{endpos}\) 集合需要对每个串分别维护。
例题 \(2.4\):[HAOI2016]找相同字符
由于不同位置算不同答案,我们需要记录 \(\text{endpos}\) 集合大小,建出 GSAM 分别维护两个串的 \(\text{endpos}\) 集合大小(设为 \(\text{siz}_s\)、\(\text{siz}_t\)),答案就是 \(\sum\text{siz}_s(u)\text{siz}_t(u)(\text{len}(u)-\text{len}(\text{fa}(u)))\)。
2.5.3 综合部分
例题 \(2.5\):[AHOI2013]差异
这题有一个做法是 SA 加单调栈,不过看起来太麻烦了,我们可以直接用 SAM 解决它。
我们看这个式子的形式就很像一个树上路径,所以肯定会往 Parent 树上想。我们发现 Parent 树上两个点的 LCA 代表了它们的最长公共后缀,那么我们发现把边权赋值为 \(\text{len}(u)-\text{len}(\text{fa}(u))\) 就可以把问题转化成树上所有路径边权和之和,这个分别计算每条边的贡献即可。但是原题问的是最长公共前缀啊?我们似乎求了一个错误的东西?其实不是的,因为很容易证明前缀的最长公共后缀与后缀的最长公共前缀是等价的。
例题 \(2.6\):[ZJOI2015]诸神眷顾的幻想乡
这个题一看可能毫无头绪,我们之前用 SAM 之类的维护的都是祖孙之间的信息,而树上路径可能会很奇形怪状。但是我们发现题目给出了一个重要的条件:叶节点不超过 \(20\) 个,所以我们可以暴力换根建 GSAM 统计了。
SAM 还经常与其他数据结构如线段树等结合变为毒瘤题。
例题 \(2.7\):[NOI2018]你的名字读者们梦寐以求的黑题终于来了
考虑一个弱化版 \(l=1,r=|s|\),我们可以补集转化一下变成求 \(s\) 和 \(t\) 的本质不同公共子串数量。我们对两个串都建出 SAM,然后按照上面的方法求出以 \(t\) 的每个点结尾的最长公共子串的长度,记作 \(\text{lcs}(i)\)。接下来对于 \(t\) 的 SAM 的每个节点分别考虑和 \(s\) 的公共子串数量即可做到不重不漏。我们设节点 \(u\) 的 \(\text{endpos}\) 集合中第一个出现的是 \(\text{fst}(u)\)(它可以在添加字符时顺便求出),那么容易发现长度比 \(\text{lcs}(\text{fst}(u))\) 大的都不能匹配,也就是贡献为 \(\max\{\text{len}(u)-\max\{\text{len}(\text{fa}(u)),\text{lcs}(\text{fst}(u))\},0\}\)。
现在我们可以考虑取一段区间怎么做了。我们可以沿用上面的思路,把 \(\text{endpos}\) 集合放到线段树上,每个点与自己的儿子合并,匹配 \(\text{lcs}\) 时判断节点对应的 \(\text{endpos}\) 集合有没有在给定区间里的。具体实现比较繁琐,可以阅读以下代码结合注释理解(其实如果你真正理解了 SAM 这题在思维难度上还是挺简单的):
const int N=1000010;
int n,m,q;char s[N],t[N];
struct SAM {//SAM板子
struct Node {
int fa,len,fst,ch[26];//fst意同上文
}tr[N];
int tot=1,lst=1;
il void Extend(int c,int pos){
int p=lst,cur=++tot;lst=cur,tr[cur].fst=pos;//整串第一次出现在当前位置
tr[cur].len=tr[p].len+1;
for(;p&&!tr[p].ch[c];p=tr[p].fa)tr[p].ch[c]=cur;
if(!p)tr[cur].fa=1;
else {
int q=tr[p].ch[c];
if(tr[q].len==tr[p].len+1)tr[cur].fa=q;
else {
int nq=++tot;tr[nq]=tr[q],tr[nq].len=tr[p].len+1;
tr[q].fa=tr[cur].fa=nq;
for(;p&&tr[p].ch[c]==q;p=tr[p].fa)tr[p].ch[c]=nq;
}
}
}
il void Clear(){
for(rg int i=1;i<=tot;i++){
tr[i].fa=tr[i].len=tr[i].fst=0;
memset(tr[i].ch,0,sizeof(tr[i].ch));
}
tot=lst=1;
}
};
SAM s1,s2;
struct Node {//权值线段树
int l,r,wei;
}tr[N*50];
int tot,rt[N];
int Merge(int u,int v,int l=1,int r=n){
if(!u||!v)return u+v;
int k=++tot;tr[k].wei=tr[u].wei+tr[v].wei;
if(l==r)return k;
ls=Merge(tr[u].l,tr[v].l,l,nmid);
rs=Merge(tr[u].r,tr[v].r,nmid+1,r);
return k;
}
void Modify(int &k,int pos,int l=1,int r=n){
if(!k)k=++tot;
tr[k].wei++;
if(l==r)return;
if(pos<=nmid)Modify(ls,pos,l,nmid);
else Modify(rs,pos,nmid+1,r);
}
int Query(int k,int L,int R,int l=1,int r=n){
if(!k)return 0;
if(L<=l&&r<=R)return tr[k].wei;
int res=0;
if(L<=nmid)res+=Query(ls,L,R,l,nmid);
if(nmid<R)res+=Query(rs,L,R,nmid+1,r);
return res;
}
struct Edge {
int to,nxt;
}e[N<<1];
int hd[N],cnt;
il void ade(int u,int v){
e[++cnt].to=v,e[cnt].nxt=hd[u],hd[u]=cnt;
}
void DFS(int u){//把子树合并上来
for(rg int i=hd[u];i;i=e[i].nxt){
int v=e[i].to;
DFS(v),rt[u]=Merge(rt[u],rt[v]);
}
}
int lcs[N];
il void LCS(int l,int r){//lcs意同上文
int p=1,len=0;
for(rg int i=1;i<=m;i++){
while(1){
if(s1.tr[p].ch[t[i]-97]){//有这个转移而且在给定范围内
if(Query(rt[s1.tr[p].ch[t[i]-97]],l+len,r)){//注意fst属于endpos,所以要加上长度
p=s1.tr[p].ch[t[i]-97],len++;break;
}
}
if(!len)break;
len--;//注意由于区间限制直接跳到父亲可能会遗漏一些情况,有一个点卡了这里
if(len==s1.tr[s1.tr[p].fa].len)p=s1.tr[p].fa;
}
lcs[i]=len;
}
}
int main(){
scanf("%s",s+1),n=strlen(s+1);
for(rg int i=1;i<=n;i++){//记录每个新加入节点的endpos
s1.Extend(s[i]-97,i),Modify(rt[s1.lst],i);
}
for(rg int i=2;i<=s1.tot;i++)ade(s1.tr[i].fa,i);
DFS(1),Read(q);//合并
for(rg int i=1,l,r;i<=q;i++){
scanf("%s",t+1),m=strlen(t+1),Read(l),Read(r);
s2.Clear();
for(rg int j=1;j<=m;j++)s2.Extend(t[j]-97,j);
LCS(l,r);
LL ans=0;
for(rg int j=2;j<=s2.tot;j++){
ans+=max(0,s2.tr[j].len-max(\//刚刚提到的式子
s2.tr[s2.tr[j].fa].len,lcs[s2.tr[j].fst]));
}
cout<<ans<<endl;
}
KafuuChino HotoKokoa
}
*3.子序列自动机
难度:题目过少,暂不明
我们现在想要构造出一个图,从它上面可以像其他自动机一样匹配,那么一个最为暴力的方案就是起点连到每个点,每个点向后面的所有点及终点连边。但是我们发现有很多边是没必要连的,例如,我们可以对于每个点的出边,指向相同字符的只保留第一个。
在具体实现中,我们记录每种字符出现的位置,对于模式串的每个字符依次二分找到最近的位置即可。
模板题核心代码:
const int N=100010;
int n,q,m,s[N];
vector<int> pos[N];
int main(){
Read(n),Read(n),Read(q),Read(m);
for(rg int i=1;i<=n;i++)Read(s[i]),pos[s[i]].pub(i);
for(rg int k=1,l;k<=q;k++){
Read(l);bool ff=1;int lst=0;
for(rg int i=1;i<=l;i++)Read(s[i]);
for(rg int i=1;i<=l;i++){
auto x=upper_bound(pos[s[i]].begin(),pos[s[i]].end(),lst);
if(x==pos[s[i]].end()){
ff=0;break;
}else lst=*x;
}
cout<<(ff?"Yes":"No")<<endl;
}
KafuuChino HotoKokoa
}
*4.Manacher 和回文自动机
难度:提高~省选
4.0 Manacher
Manacher 是一种用于求解一个字符串的回文子串的神奇算法。
回文串分为奇数长度和偶数长度,但我们发现偶数长度的可以通过添加辅助字符等方式转化为奇数,所以我们接下来只讨论长度为奇数,也就是以某个字符为对称中心的回文串。
现在我们要求出以每个位置为对称中心的最长回文串的半径长度,而朴素的算法是 \(O(n^2)\) 的,我们还是需要考虑尽可能多地利用已经求出的信息,假设我们记录了右端点最靠右的回文子串,那么如图:
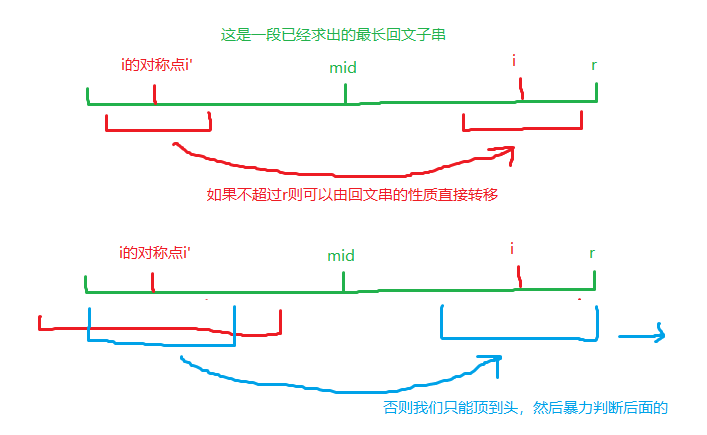
显然右端点是单调递增的,所以复杂度是 \(\mathcal O(n)\)。
模板题核心代码:
const int N=22000010;
int len=1,ans=1,r,mid,p[N];
char c,s[N];
int main(){
s[0]='#',s[len]='@',c=getchar();
while(c<'a'||c>'z')c=getchar();
while(c>='a'&&c<='z'){
s[++len]=c,s[++len]='@',c=getchar();
}
for(rg int i=1;i<=len;i++){
if(i<=r)p[i]=min(p[(mid<<1)-i],r-i+1);//先更新到最右
while(s[i-p[i]]==s[i+p[i]])++p[i];//然后暴力看外面的部分
if(i+p[i]>r)r=i+p[i]-1,mid=i;//更新右端点及答案
if(p[i]>ans)ans=p[i];
}
cout<<ans-1<<endl;
return 0;
}
4.1 回文自动机
回文自动机(PAM),也可以叫做回文树,它存储了一个字符串的所有回文子串。
PAM 也是由状态之间的转移边和后缀链接构成,每个状态代表了一个回文子串,转移边是在该节点代表的串的两端加一个相同的字符(因为是回文串),后缀链接指向的是该节点的最长回文后缀。与 Manacher 不同,这里我们将奇串和偶串分开建两个根会更好考虑,偶根的后缀链接是奇根,奇根不需要后缀链接(必然不会失配)。
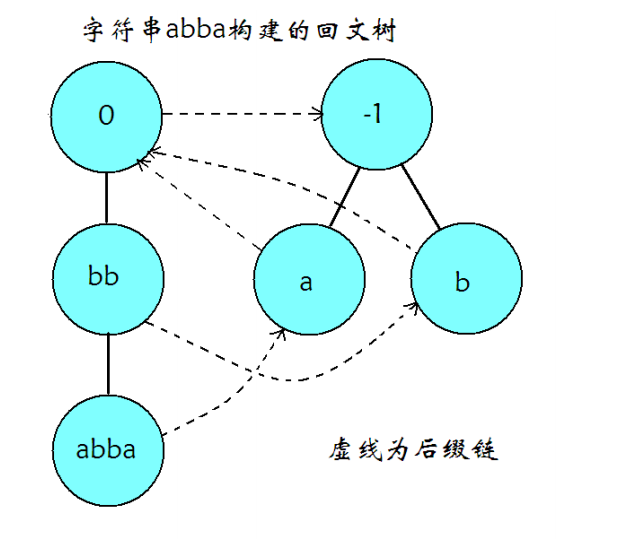
(嫖个图,这便是 PAM 的基本构造了)
与 SAM 一样,我们考虑如何增量构造它。
这里的构造方式非常简单,我们只需要从上一个字符的最长回文子串开始不断跳后缀链接跳到可行的回文子串即可(图中的 \(A\)),而这个新节点的后缀链接应指向这个串的最长回文后缀,我们同样可以直接跳后缀链接跳到 \(B\)。
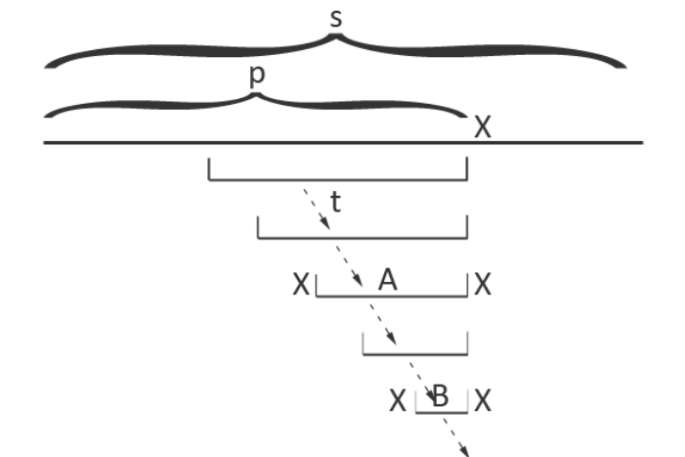
我们有一个定理是说一个字符串的本质不同回文子串个数不超过它的长度,由数学归纳法易证。所以 PAM 的状态数对应也是线性的,由于每个节点只代表一个不同的回文子串,所以到它的转移数也是线性的。
容易发现它的节点个数(去除两个根)就是本质不同的回文子串个数,以某个点结尾的本质不同回文子串个数就是它在 Parent 树上的深度。
模板题核心代码:
const int N=500010;
char s[N];int n,k;
struct Node {
int fa,dep,len,ch[26];
}tr[N];
int tot=1,lst=1;//0为偶根,1为奇根
il int Find(int pos,int u){//跳后缀链接
while(s[pos-tr[u].len-1]!=s[pos])u=tr[u].fa;
return u;
}
il void Extend(int pos,int c){//添加字符,过程在上面说得很清楚了
int cur,p=Find(pos,lst);
if(!tr[p].ch[c]){
tr[cur=++tot].len=tr[p].len+2;
int q=Find(pos,tr[p].fa);tr[cur].fa=tr[q].ch[c];
tr[cur].dep=tr[tr[cur].fa].dep+1,tr[p].ch[c]=cur;
}
lst=tr[p].ch[c];
}
int main(){
tr[1].len=-1,tr[0].fa=1;//注意初始化
scanf("%s",s+1),n=strlen(s+1);
for(rg int i=1;i<=n;i++){
s[i]=(s[i]-97+k)%26+97;
Extend(i,s[i]-97);
cout<<(k=tr[lst].dep)<<" ";
}
KafuuChino HotoKokoa
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号