The 2025 ICPC Asia East Continent Online Contest (II)
A
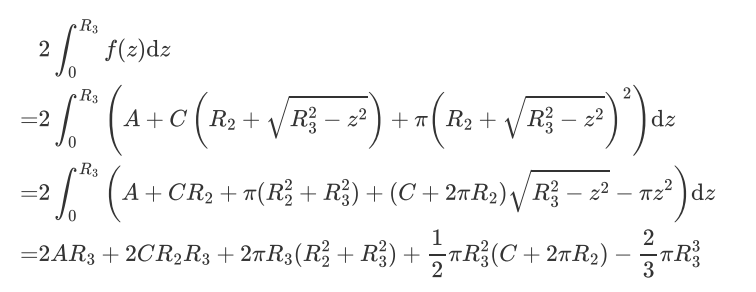
const int N=1e5+10;
const double pi=acos(-1);
struct node{
int x,y;
node(){x=y=0;}
node(int xx,int yy){x=xx,y=yy;}
bool operator==(const node&rhs)const{return x==rhs.x&&y==rhs.y;}
double operator*(const node&rhs)const{return 1.0*x*rhs.y-1.0*y*rhs.x;}
node operator+(const node&rhs)const{return node(x+rhs.x,y+rhs.y);}
node operator-(const node&rhs)const{return node(x-rhs.x,y-rhs.y);}
bool operator<(const node&rhs)const{return x!=rhs.x?x<rhs.x:y<rhs.y;}
}a[N],h[N];
double dis(node x,node y){return sqrt(1.0*(x.x-y.x)*(x.x-y.x)+1.0*(x.y-y.y)*(x.y-y.y));}
int st[N],top=0;
bool vis[N];
void sol()
{
int n=read();double R2=read(),R3=read();
for(int i=1;i<=n;i++)a[i].x=read(),a[i].y=read();
for(int i=1;i<=n+1;i++)st[i]=0;
for(int i=1;i<=n;i++)vis[i]=0;top=0;
sort(a+1,a+n+1);n=unique(a+1,a+n+1)-a-1;
st[++top]=1;
for(int i=2;i<=n;i++)
{
while(top>=2&&(a[st[top]]-a[st[top-1]])*(a[i]-a[st[top]])<=0)vis[st[top--]]=0;
vis[i]=1;
st[++top]=i;
}
int tmp=top;
for(int i=n-1;i;i--)if(!vis[i])
{
while(top>tmp&&(a[st[top]]-a[st[top-1]])*(a[i]-a[st[top]])<=0)vis[st[top--]]=0;
vis[i]=1;
st[++top]=i;
}
for(int i=1;i<=top;i++)h[i]=a[st[i]];
int cnt=top-1;
double A=0,C=0;
for(int i=1;i<=cnt;i++)C+=dis(h[i],h[i+1]);
for(int i=1;i<=cnt;i++)A+=h[i]*h[i+1]/2;
double Ans=2.0*A*R3+2.0*C*R2*R3+2*pi*R3*(1.0*R2*R2+1.0*R3*R3)+0.5*pi*R3*R3*(C+2*pi*R2)-2.0/3.0*pi*R3*R3*R3;
printf("%.9Lf\n",Ans);
}
int main()
{
int T=read();
while(T--)sol();
return 0;
}
B
考虑层分别做
这是一个匹配问题,可以行列连边,然后上下界费用流
不会写咋办?正难则反,考虑保留最多的,限制从 \(S\) 到 \(i\) 至少流 \(1\) 变成 \(S\) 到 \(i\) 至多流 \(c-1\),\(c\) 表示这一行有几列是能用的,列同理,最大费用流即可。
namespace MCMF
{
const int N=5e3+10,M=1e5+10,inf=0x3f3f3f3f3f3f3f3f;
int head[N],ver[M],nxt[M],tot=1,edge[M],cost[M];
bool vis[N];
void init(){memset(head,0,sizeof(head));tot=1;}
void add0(int x,int y,int z,int c)
{
ver[++tot]=y,edge[tot]=z,cost[tot]=c;
nxt[tot]=head[x],head[x]=tot;
}
void add(int x,int y,int z,int c)
{
// printf("add(%lld, %lld, %lld, %lld)\n",x,y,z,c);
add0(x,y,z,c),add0(y,x,0,-c);
}
int dis[N],cur[N];
bool spfa(int s,int t)
{
memset(dis,-0x3f,sizeof(dis));
memcpy(cur,head,sizeof(head));
queue<int> que;que.push(s),dis[s]=0;
while(!que.empty())
{
int x=que.front();que.pop();
vis[x]=0;
for(int i=head[x];i;i=nxt[i])
{
int y=ver[i],z=edge[i],c=cost[i];
if(z&&dis[x]+c>dis[y])
{
dis[y]=dis[x]+c;
if(!vis[y])vis[y]=1,que.push(y);
}
}
}
return dis[t]>=0;
}
int res=0;
int dfs(int x,int t,int limit)
{
if(x==t||!limit)return limit;
int flow=0,rlow=0;vis[x]=1;
for(int &i=cur[x];i;i=nxt[i])
{
int y=ver[i],z=edge[i],c=cost[i];
if(z&&!vis[y]&&dis[x]+c==dis[y])
{
rlow=dfs(y,t,min(limit,z));
if(rlow)flow+=rlow,limit-=rlow,edge[i]-=rlow,edge[i^1]+=rlow,res+=rlow*c;
if(!limit)break;
}
}
vis[x]=0;
return flow;
}
pii dinic(int s,int t)
{
int ans=0;res=0;
while(spfa(s,t))
{
int x=0;
while(x=dfs(s,t,inf))ans+=x;
}
// ans:maxflow res:mincost
return mp(ans,res);
}
}
using namespace MCMF;
const int NN=1010;
int val[NN],L,W,H;
char a[NN][NN],b[NN][NN],c[NN][NN];
int id(int i,int j,int k){return ((i-1)*W+j-1)*H+k;}
struct node{
int x,y,z;
node(){x=y=z=0;}
node(int xx,int yy,int zz){x=xx,y=yy,z=zz;}
};
void sol()
{
L=read(),W=read(),H=read();
for(int i=1;i<=L*W*H;i++)val[i]=read();
for(int i=1;i<=H;i++)scanf("%s",a[i]+1);
for(int i=1;i<=H;i++)scanf("%s",b[i]+1);
for(int i=1;i<=W;i++)scanf("%s",c[i]+1);
bool flag=1;
ll ans=0;
vector<node>Ans;
for(int k=1;k<=H;k++)
{
init();
tot=1;
memset(head,0,sizeof(head));
int s=0,t=L+W+1;
for(int i=1;i<=L;i++)
{
if(!(a[k][i]^48))continue;
int cnt=0;
for(int j=1;j<=W;j++)
{
if(!(b[k][j]^48))continue;
cnt+=c[j][i]^48;
}
if(!cnt){flag=0;break;}
add(s,i,cnt-1,0);
}
if(!flag)break;
for(int j=1;j<=W;j++)
{
if(!(b[k][j]^48))continue;
int cnt=0;
for(int i=1;i<=L;i++)
{
if(!(a[k][i]^48))continue;
cnt+=c[j][i]^48;
}
if(!cnt){flag=0;break;}
add(j+L,t,cnt-1,0);
}
if(!flag)break;
int sum=0;
for(int i=1;i<=L;i++)for(int j=1;j<=W;j++)if((a[k][i]^48)&&(b[k][j]^48)&&(c[j][i]^48))
{
sum+=val[id(i,j,k)];
add(i,j+L,1,val[id(i,j,k)]);
}
pii tmp=dinic(s,t);
for(int x=1;x<=L;x++)
{
for(int i=head[x];i;i=nxt[i])
{
int y=ver[i],z=edge[i];
if(!y)continue;
if(z)Ans.pb(node(x,y-L,k));
}
}
ans+=sum-tmp.se;
}
if(!flag){puts("NO");return;}
puts("YES");
printf("%lld\n%lld\n",ans,(int)Ans.size());
for(node it:Ans)printf("%lld %lld %lld\n",it.x,it.y,it.z);
}
signed main()
{
int T=read();
while(T--)sol();
return 0;
}
C
队友写的,回头补
D
肯定是从大到小选,分开考虑每个点的贡献,最后二项式定理能推出来一个式子,\(\mathcal O(n)\) 即可。
E
队友写的,回头补
H
考虑长度为 \(l\) 的链,容斥可以求出有多少种排列方式使得选择的 最短的操作序列 是 \(l\)。
然后 \(\mathcal O(n^2)\) 求出树上有多少个长度为 \(i\) 的链即可。
J
队友写的,回头补
K
外子树 dp
考虑 \(f(i,j)\) 表示 \(i\) 子树内,包含 \(i\),大小为 \(j\) 的连通块数量,\(g(i,j)\) 表示子树外,\(f\) 树形背包求出,\(g\) 可通过 \(f\) 转移。
精细处理上界(\(sz_i\))可将 \(g\) 和 \(f\) 做到一个复杂度。
const int N=3010,M=N<<1,mod=998244353;
void Add(int &x,int y){x+=y;if(x>=mod)x-=mod;}
void Sub(int &x,int y){x-=y;if(x<0)x+=mod;}
int head[N],ver[M],nxt[M],tot=0;
void add(int x,int y)
{
ver[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
vi mul(vi a,vi b)
{
vi ans(a.size()+b.size()-1,0);
for(int i=0;i<(int)a.size();i++)for(int j=0;j<(int)b.size();j++)Add(ans[i+j],1ll*a[i]*b[j]%mod);
return ans;
}
int sz[N],Ans;vi f[N],g[N],pre[N],suf[N];
void dfs(int x,int fa)
{
sz[x]=1;
f[x]=vi{0,1};
vi son;
for(int i=head[x];i;i=nxt[i])
{
int y=ver[i];if(y==fa)continue;
son.pb(y);
dfs(y,x);
sz[x]+=sz[y];
f[y][0]=1,f[x]=mul(f[x],f[y]),f[y][0]=0;
}
}
void dfs1(int x,int fa)
{
int cnt=0;vi son;
for(int i=head[x];i;i=nxt[i])
{
int y=ver[i];if(y==fa)continue;
son.pb(y),cnt++;
}
for(int i=0;i<cnt;i++)
{
int y=son[i];
f[y][0]=1;
if(i==0)pre[i]=f[y];
else pre[i]=mul(pre[i-1],f[y]);
f[y][0]=0;
}
for(int i=cnt-1;~i;i--)
{
int y=son[i];
f[y][0]=1;
if(i==cnt-1)suf[i]=f[y];
else suf[i]=mul(suf[i+1],f[y]);
f[y][0]=0;
}
if(!fa)g[x]=vi(1);
g[x][0]=1;
for(int i=0;i<cnt;i++)
{
int y=son[i];
g[y]=mul(g[x],vi{0,1});
g[y].resize(sz[y]+1);
if(i)g[y]=mul(g[y],pre[i-1]),g[y].resize(sz[y]+1);
if(i<cnt-1)g[y]=mul(g[y],suf[i+1]),g[y].resize(sz[y]+1);
}
g[x][0]=0;
for(int y:son)dfs1(y,x);
}
void dfs2(int x,int fa)
{
for(int i=1;i<(int)f[x].size();i++)Add(Ans,f[x][i]);
for(int i=head[x];i;i=nxt[i])
{
int y=ver[i];if(y==fa)continue;
dfs2(y,x);
for(int j=1;j<(int)min(g[y].size(),f[y].size());j++)Sub(Ans,1ll*g[y][j]*f[y][j]%mod);
}
}
void sol()
{
int n=read();
tot=0;for(int i=1;i<=n;i++)head[i]=0;
for(int i=1;i<n;i++)
{
int u=read(),v=read();
add(u,v),add(v,u);
}
for(int i=1;i<=n;i++)vi().swap(f[i]),vi().swap(g[i]),vi().swap(pre[i]),vi().swap(suf[i]);
Ans=0;dfs(1,0),dfs1(1,0),dfs2(1,0);
printf("%d\n",Ans);
}
int main()
{
// freopen("1.in","r",stdin);
int T=read();
while(T--)sol();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号