LOJ#10045. 「一本通 2.2 练习 1」Radio Transmission

UPD：更新了一种推导方法，但原推导方法没有删除。

为下文表述方便，这里做出一些约定：

1. 字符串下标从 \(1\) 开始
2. \(l\) 代表题目给定字符串 \(s\) 的长度；
3. \(\operatorname{next}\) 代表 KMP 算法的失配函数，\(\operatorname{next}(i)\) 表示 \(s_{1\dots i}\) 的最长公共前缀后缀的长度；
4. 对于两个字符串 \(s_1,s_2\)，\(s_1+s_2\) 代表将两个字符串拼接起来，如 \(\mathtt{abc}+\mathtt{defg}=\mathtt{abcdefg}\)。

---

题目传送门

推导方法一：

令最短循环节为 \(s_1\)，字符串结尾残缺的一段循环节为 \(s_2\)，\(s_2\) 变成循环节需要补上的串为 \(s_3\)。根据定义，可得 \(s_1=s_2+s_3\)。

有了上面的定义，这道题给出的字符串 \(s\) 就可以表示为 \(s_1,s_1,\dots,s_1,s_2\) 的形式。将 \(s\) 中的所有 \(s_1\) 拆成 \(s_2\) 和 \(s_3\)，此时 \(s=s_2,s_3,s_2,s_3,\cdots,s_2,s_3,s_2\)。

通过这一些列拆分，我们很容易得出 \(s\) 的最长公共前缀后缀：\(\rlap{\overbrace{\phantom{s_2,s_3,s_2,s_3,\cdots,s_2}}^{\text{prefix}}}s_2,s_3,\underbrace{s_2,s_3,\cdots,s_2,s_3,s_2}_{\text{suffix}}\)

观察发现当 \(s\) 扔掉后缀（suffix）后，剩下 \(s_2\) 和 \(s_3\)，放在一起就是 \(s_1\)，也就是我们要求的循环节。

综上，最短循环节长度为 \(l-\operatorname{next}(l)\)。

---

推导方法二：

请确保用 KMP 算法做完 POJ2406 了之后再读这个推导方法。

从 POJ2406 这道题，我们知道：对于一个长度为 \(l\) 的字符串 \(s\)（假设它的下标从 \(1\) 开始），它的最短循环节长度是 \(l-\operatorname{next}(l)\)。

虽然这道题的字符串是不完整的，但上面的结论仍然成立。下面我们来推导一下为什么：

令 \(s=\mathtt{abcabcabc}\)，这时 \(s_{1\dots 6}=s_{4\dots 9}\)，\(\operatorname{next}(9)=6\)。
去掉 \(s\) 的最后一个字符 \(\mathtt c\)，此时 \(s=\mathtt{abcabcab}\)，\(s_{1\dots 5}=s_{4\dots 8}\)，\(\operatorname{next}(8)=5\)。
再去掉 \(s\) 的最后一个字符 \(b\)，此时 \(s=\mathtt{abcabca}\)，\(s_{1\dots 4}=s_{4\dots 7}\)，\(\operatorname{next}(7)=4\)。

发现什么规律了吗？每当我们将 \(s\) 的长度减一，\(\operatorname{next}(l)\) 也会随着减一，\(l-\operatorname{next}(l)\) 一直不变，算出的一直是完整字符串的答案。

配合着图再仔细理解一下：

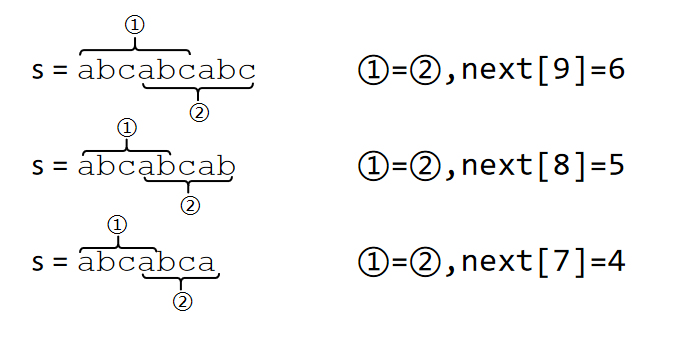
至于 \(\operatorname{next}(l)\) 为什么会随着长度递减，多看看这张图大概就理解了……

说了这么多，来看看这道题的完整代码：（其实核心代码只有一行qaq）

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e6;
char s[N+10];
int nxt[N+10],n;
void init()
{
	memset(nxt,0,sizeof(nxt));
	int n=strlen(s);
	for(int i=1;i<n;i++)
	{
		int j=nxt[i-1];
		while(j && s[i]!=s[j]) j=nxt[j-1];
		if(s[i]==s[j]) j++;
		nxt[i]=j;
	}
}
int main()
{
	scanf("%d%s",&n,s);
	init();
	printf("%d\n",n-nxt[n-1]);
	return 0;
}