二叉树的中序遍历 递归与非递归

94. 二叉树的中序遍历

给定一个二叉树的根节点 root ，返回它的 中序 遍历。

示例 1：

输入：root = [1,null,2,3]

输出：[1,3,2]

示例 2：

输入：root = []

输出：[]

示例 3：

输入：root = [1]

输出：[1]

示例 4：

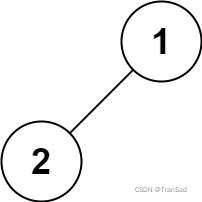
输入：root = [1,2]

输出：[2,1]

示例 5：

输入：root = [1,null,2]

输出：[1,2]

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

思路：

  二叉树的前中后序遍历是算法与数据结构的必备基础了。

  因为在学习算法和数据结构早期，我们就是通过这几种不同的遍历顺序来学习递归的。首先讲一下递归的实现：①定义base case ②根据那种遍历，写顺序（中序遍历就是“左右中”的顺序即可。）

代码（递归）：

class Solution(object):

    def inorderTraversal(self, root):

        res=[]

        def zhong(root):

            if not root:return#base case

            zhong(root.left)#左

            res.append(root.val)#中

            zhong(root.right)#右

        zhong(root)

        return res

注意到有个进阶要求: 递归算法很简单，你可以通过迭代算法完成吗？

  其实用非递归的方式实现二叉树的遍历并不算是偏难要求，在面试过程中，用非递归实现二叉树的前中后序遍历是很高频的问题。

  我们可以通过栈来辅助实现非递归形式下的二叉树遍历。虽然前中后序遍历的递归方法并不是非常相似（如果要去理解如何迭代的思路迭代话），但经过特定的总结和整合，我们现在可以只用一个模板，只改一个地方来实现非递归下三种不同的遍历方式。

  接下来这个模板是我在众多模板中分析得到的最简单明了的一种，我不打算从逻辑上去解释这个过程了，只需要记下这个模板，后续不管是那种顺序的遍历，都可以直接用这么一段代码非递归地实现。

代码（非递归）：

class Solution(object):

    def inorderTraversal(self, root):

        stack=[root]#

        res=[]#结果列表

        while(stack):

            node = stack.pop()#栈，弹出

            if isinstance(node,TreeNode):#判断node是一个节点还是一具体值

                stack.extend([node.right,node.val,node.left])#重点

            elif isinstance(node,int):#如果是具体值

                res.append(node)#添加进结果列表

        return res

  就是这么一段模板，可以去理解，但理解过后的几个月你又会忘掉（我就是这样）。直接从代码上来看，这段模板还是非常好记忆的。在一个栈里初始化我们的根节点root，不断地弹出栈，判断弹出元素的类型，如果是节点类型的话就按一定顺序把它的值和他的左右节点压入栈，如果是int类型的话，直接把值压入栈。

  唯一要注意的一点是，我们这里是中序遍历，中序遍历的顺序是“左中右”，在这里我们压入栈的时候，要改成相反的顺序，即“右中左”。

  同理，如果是前序遍历，本该是“中左右”，压入顺序是“右左中”；如果是后序遍历，本该是“左右中”，压入顺序是“中右左”，其他处代码一模一样。这就是这套非递归实现不同种遍历模板的强大之处，强烈建议记住。