常用算法的总结——链表

链表常用算法：快慢指针、利用HashMap、栈

如：

1 快慢指针

1) 输入链表头节点，奇数长度返回中点，偶数长度返回上中点
2) 输入链表头节点，奇数长度返回中点，偶数长度返回下中点
3) 输入链表头节点，奇数长度返回中点前一个，偶数长度返回上中点前一个
4) 输入链表头节点，奇数长度返回中点前一个，偶数长度返回下中点前一个

第一题代码如下，其他同理：

// head头
public static Node mi d0rUpMi dNode(Node head) {
    if (head == nu11|I head.next == nu11Il| head.next.next == nu1l) {
　　　　return head;
　　}
　　Node slow = head . next;
　　Node fast = head. next . next; 
　　while (fast.next != nu11 && fast. next.next != nu11) {
　　　　slow = slow. next;
　　　　fast = fast. next. next;
　　}
　　return slow;
}

2 给定一个单链表的头节点head，请判断该链表是否为回文结构。

1) 哈希表方法特别简单——利用栈

public static boolean isPalindrome1 (Node head) {
　　Stack<Node> stack = new Stack<Node>( );
　　Node cur = head;
　　while (cur != nu1l) {
　　　　stack. push(cur);
　　　　cur = cur. next;
　　}
　　while (head != nu1l) {
　　　　if (head.value != stack. pop().value) {
　　　　　　return false;
　　　　}
　　　　head = head. next;
　　}
　　return true;
}

2) 改原链表的方法就需要注意边界了

3) 利用快慢指针的算法：先让快指针到终点，慢指针到中点，然后让指向中点的慢指针指向null，后半部分全部倒转，后面的指向前面的，最后由终点和起点开始往中间遍历，只要有一步不相等就返回false，最后由如果需要恢复则将其恢复成原样，代码如下（包含了最后恢复成原样的步骤）：

public static boolean isPalindrome3(Node head) {
        if (head == null | head.next == null) {
            return true;
        }
        Node n1 = head;
        Node n2 = head;
        while (n2.next != null && n2.next.next != null) { // find mid node
            n1 = n1.next; // n1 -> mid
            n2 = n2.next.next; // n2 -> end
        }
        n2 = n1.next; // n2 -> right part first node
        n1.next = null; // mid.next -> null
        Node n3 = null;
        while (n2 != null) { // right part convert
            n3 = n2.next; // n3 -> save next node
            n2.next = n1; // next of right node convert
            n1 = n2;//n1move
            n2 = n3;//n2move
        }
        n3 = n1; // n3 -> save last node
        n2 = head;// n2 -> left first node .
        boolean res = true;
        while (n1 != null && n2 != null) { // check palindrome
            if (n1.value != n2. value) {
                res = false;
                break ;
            }
            n1 = n1.next; // left to mid
            n2 = n2.next; // right to mid
        }
        n1 = n3.next;
        n3.next = null;
        while (n1 != null) { // recover list
            n2 = n1. next;
            n1.next = n3;
            n3 = n1;
            n1 = n2;
        }
        return res;

    }

 3 

将单向链表按某值划分成左边小、中间相等、右边大的形式

　　方法：把链表放入数组里，在数组上做partition ，代码如下：

public static Node listPartition1(Node head, int pivot) {
        if (head == null) {
            return head;
        }
        Node cur = head;
        int i = 0;
        while (cur != null) {
            i++;
            cur = cur.next;
        }
        Node[] nodeArr = new Node[i];
        i = 0;
        cur = head;
        for (i = 0; i != nodeArr.length; i++) {
            nodeArr[i] = cur;
            cur = cur.next;
        }
　　　　//将数组进行交换，大于pivot的放pivot左边，反之放右边
        arrPartition(nodeArr, pivot);
        for (i = 1; i != nodeArr.length; i++) {
            nodeArr[i - 1].next = nodeArr[i];
        }
        nodeArr[i - 1].next = null;
        return nodeArr[0];
    }

public static int[] arrPartition(int[] arr, int L, int R, int p) {
    int less = L - 1;
    int more = R + 1;
    while(L < more) {
        if(arr[L] < p) {
            swap(arr, ++less, L++);
        } else if (arr[L] > p) {
            swap(arr, --more, L);
        } else {
            L++;
        }
    }
    return new int[] { less + 1, more - 1 };
}

public static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

 

4 利用HashMap

一种特殊的单链表节点类描述如下
class Node {
　　int value;
　　Node next;
　　Node rand;
　　Node(int val) { value = val;

}
rand指针是单链表节点结构中新增的指针，rand可 能指向链表中的任意一个节 点，也可能指向null。
给定一个由Node节点类型组成的无环单链表的头节点head,请实现一个函数完成这个链表的复制，并返回复制的新链表的头节点。

代码如下：

    public static Node copyListWithRand1 (Node head) {
        HashMap<Node, Node> map = new HashMap<Node, Node>();
        Node cur = head;
        while (cur != null) {
            map . put(cur, new Node( cur.value));
            cur = cur.next;
        }
        cur =
                head;
        while (cur != null) {
            // cur 老
            // map.get(cur) 新
            map.get(cur).next = map. get(cur.next);
            map. get(cur).rand = map. get(cur.rand);
            cur = cur.next ;
        }
        return map . get(head);
    }

[进阶] 时间复杂度O(N)，额外空间复杂度0(1)

方式2：保证时间复杂度的前提下，不使用大的空间

public static Node copyListWithRand2(Node head) {
        if (head == null) {
            return null;
        }
        Node cur = head;
        Node next = null;
        // copy node and link to every node
        // 1-> 2
        //1->1'->2
        while (cur != null) {
            // cur老
            next = cur.next;
            cur.next = new Node(cur.value);
            cur.next.next = next;
            cur = next;
        }
        cur = head;
        Node curCopy = null;
        // set copy node rand 搞定rand结点
        //1->1'->2->2'
        while (cur != null) {
            // cur老
            // cur.next  新copy
            next = cur.next.next;
            curCopy = cur.next;
            curCopy.rand = cur.rand != null ? cur.rand.next : null;
            cur = next;
        }
        //返回结果的头结点要为head的下一个
        Node res = head.next;
        cur = head;

        // split，搞定next结点
        while (cur != null) {
            next = cur.next.next;
            curCopy = cur.next;
            cur.next = next;
            curCopy.next = next != null ? next.next : null;
            cur = next;

        }
        return res;

    }

5 相交链表

给定两个可能有环也可能无环的单链表，头节点head1和head2。请实现一个函数，如果两个链表相交，请返回相交的第一个节点。如果不相交，返回null

[要求]如果两个链表长度之和为N，时间复杂度请达到O(N)，[进阶]额外空间复杂度请达到O(1)。

5.1 无环情况下解法：head1、end1为第一个链表的头结点、尾结点，head2、end2为第二个链表的头结点、尾结点，判断end1是否为end2，不是则直接返回null（两者必不相交）；是的话，长链表先走长链表比短链表长的部分（如长链表为100，短链表为80，则长链表先走20步），然后同时走，他们一定会在第一个结点相遇，代码如下：

    //如果两个链表都无环，返回第-一个相交节点，如果不想交，返回null
    public static Node noLoop(Node head1, Node head2) {
        if (head1 == null || head2 == null) {
            return null;
        }
        Node cur1 = head1;
        Node cur2 = head2;
        //n为差值
        int n = 0;
        while (cur1.next != null) {
            n++;
            cur1 = cur1.next;
        }
        while (cur2.next != null) {
            n--;
            cur2 = cur2.next;
        }
        //此时cur1、cur2分别到达链表1、2的末尾，
        if (cur1 != cur2) {
            return null;
        }

        // n :链表1长度减去链表2长度的值
        cur1 = n > 0 ? head1 : head2; //谁长，谁的头变成cur1
        cur2 = cur1 == head1 ? head2 : head1; //谁短，谁的头变成cur2
        n = Math.abs(n);
        //先走差值的步骤
        while (n != 0) {
            n--;
            cur1 = cur1.next;
        }
        //再同时一块走
        while (cur1 != cur2) {
            cur1 = cur1.next;
            cur2 = cur2.next;
        }
        return cur1;

    }

5.2 有环的情况下解法

分析：①两条不想交的有环链表；②两条相交点为同一点；③相交点为不同点；三种情况图示如下：②其实和无环情况一样，只需要把cur1、cur2到达末尾改成到达公共结点即可

 

 

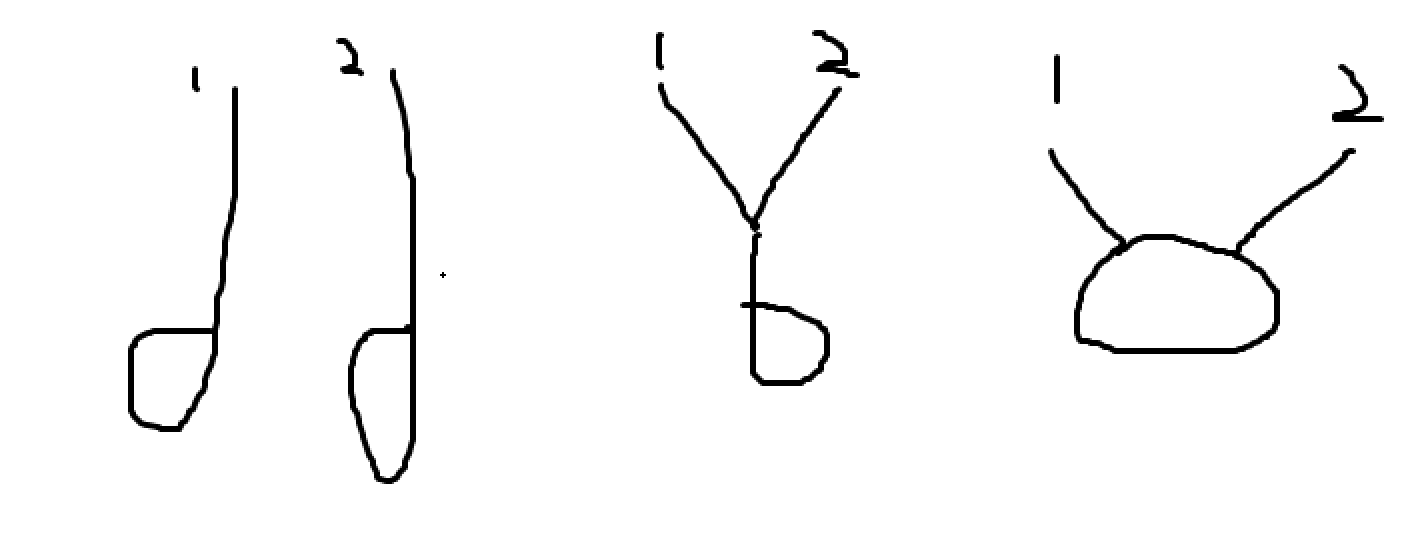
代码如下：

/** 两个有环链表， 返回第一个相交节点，如果不想交返回null
     * @param head1 1的头
     * @param loop1 1的入环
     * @param head2 2的头
     * @param loop2 2的入环
     * @return 返回相交结点，情况③的话有两个，返回任意一个即可
     */
    public static Node bothLoop(Node head1, Node loop1, Node head2, Node loop2) {
        Node cur1 = null;
        Node cur2 = null;
        //这部分的代码其实和无环的类似，只不过把while循环的终止条件改成到达入环的结点
        if (loop1 == loop2) {//说明相交点在环外，为情况②
            cur1 = head1;
            cur2 = head2;
            int n = 0;
            while (cur1 != loop1) {
                n++;
                cur1 = cur1.next;
            }
            while (cur2 != loop2) {
                n--;
                cur2 = cur2.next;
            }
            cur1 = n > 0 ? head1 : head2;
            cur2 = cur1 == head1 ? head2 : head1;
            n = Math.abs(n);
            while (n != 0) {
                n--;
                cur1 = cur1.next;
            }
            while (cur1 != cur2) {
                cur1 = cur1.next;
                cur2 = cur2.next;
                return cur1;
            }
        }
        else {//情况①和情况③
            cur1 = loop1.next;
            //开始从入环结点处开始遍历这个环，
            // 如果找到另外一个入环结点，则为情况③，返回任意一个入环结点即可
            while (cur1 != loop1) {
                if (cur1 == loop2) {
                    return loop1;
                }
                cur1 = cur1.next;
            }
            //如果没找到，则说明为情况①，返回null
            return null;

        }
    }

5.3 汇总有环和无环情况

总的方法如下：

public static Node getIntersectNode(Node head1, Node head2) {
        if (head1 == null|| head2 == null) {
            return null;
        }
        //getLoopNode()为获取入环结点的方法
        Node loop1 = getLoopNode (head1);
        Node loop2 = getLoopNode (head2);
        //如果两个链表的入环结点都为空，则说明二者都为无环链表
        if (loop1 == null && loop2 == null) {
            return noLoop( head1, head2);
        }
        //如果两个链表的入环结点都不为空，则说明二者都为有环链表
        if (loop1 != null && loop2 != null) {
            return bothLoop(head1, loop1, head2, loop2);
        }
        //其他情况都不可能相交
        return null;
    }

5.4 里面的获取入环结点的方法如下（其实这也是一道简单的面试题，代码省略了）：

链表是否有环，有则找到入环结点，没有则返回null

解法一：HashSet

利用HashSet的唯一性，遍历链表，不存在则放入，存在则说明有环，没有环一定会返回null，图示如下：

 

 

 

 

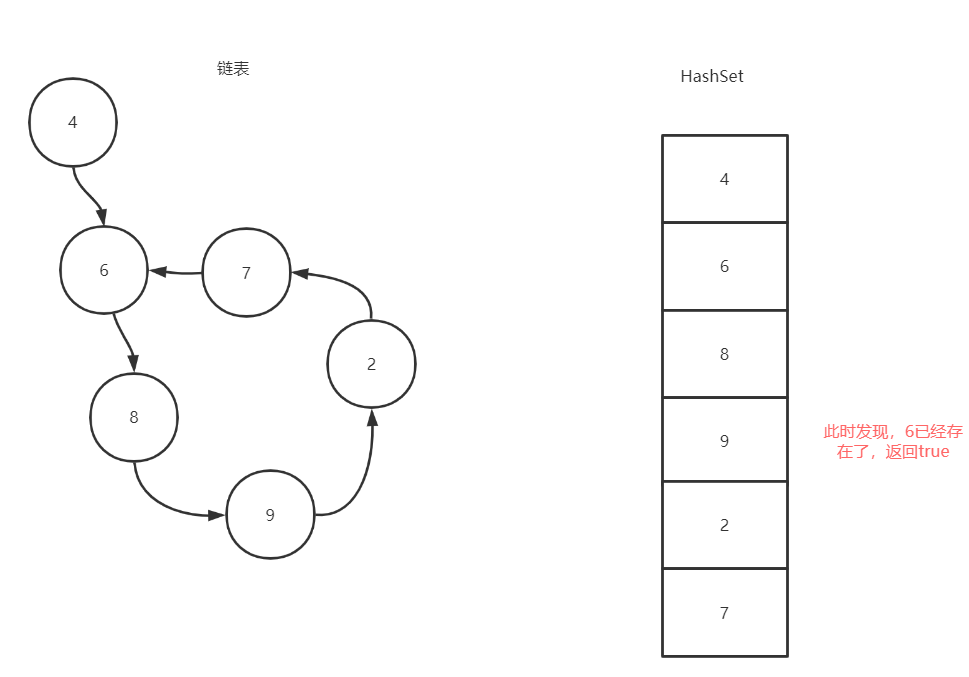
 解法二：快慢指针

慢指针走一步，快指针走两步，那么一定会在某个点相遇，此时让快指针回到开头，变成一次走一步，两者同时出发（此时慢指针在相遇的点），两个慢指针就必然会在入环的点相遇

 

6 删除链表结点

能不能不给单链表的头节点，只给想要删除的节点，就能做到在链表上把这个点删掉?

抖机灵的做法：给出要删除的结点，把该节点的next赋值给该节点，然后让该节点跨过下一个结点，让next指针指向下下一个节点

其实这样本质上并没有把自己删除掉，除此之外，尾巴结点删除不掉

其实这样是不行的，只能给出头结点才能解决。