H - Crystalfly

传送门

题意:
给一棵 n 个点带点权的树从 1 号点出发，每个点的点权可以吃一次，要求最大化吃到的点权和。每个点还有另一个值\(t_i\)当你走到这个点的相邻节点时，这个点会被开始倒计时，如果在倒计时结束前还没能吃到这个点，那这个点的点权会消失（注意，可以经过，只是吃不到点权）。 其中 1 <= \(t_i\) <= 3

---

思路:
1 <= t <= 3就可以有两种结果
儿子节点1 <= t <= 2只有一个点可以经过
儿子节点1 <= t <= 3可以进行一次来会操作

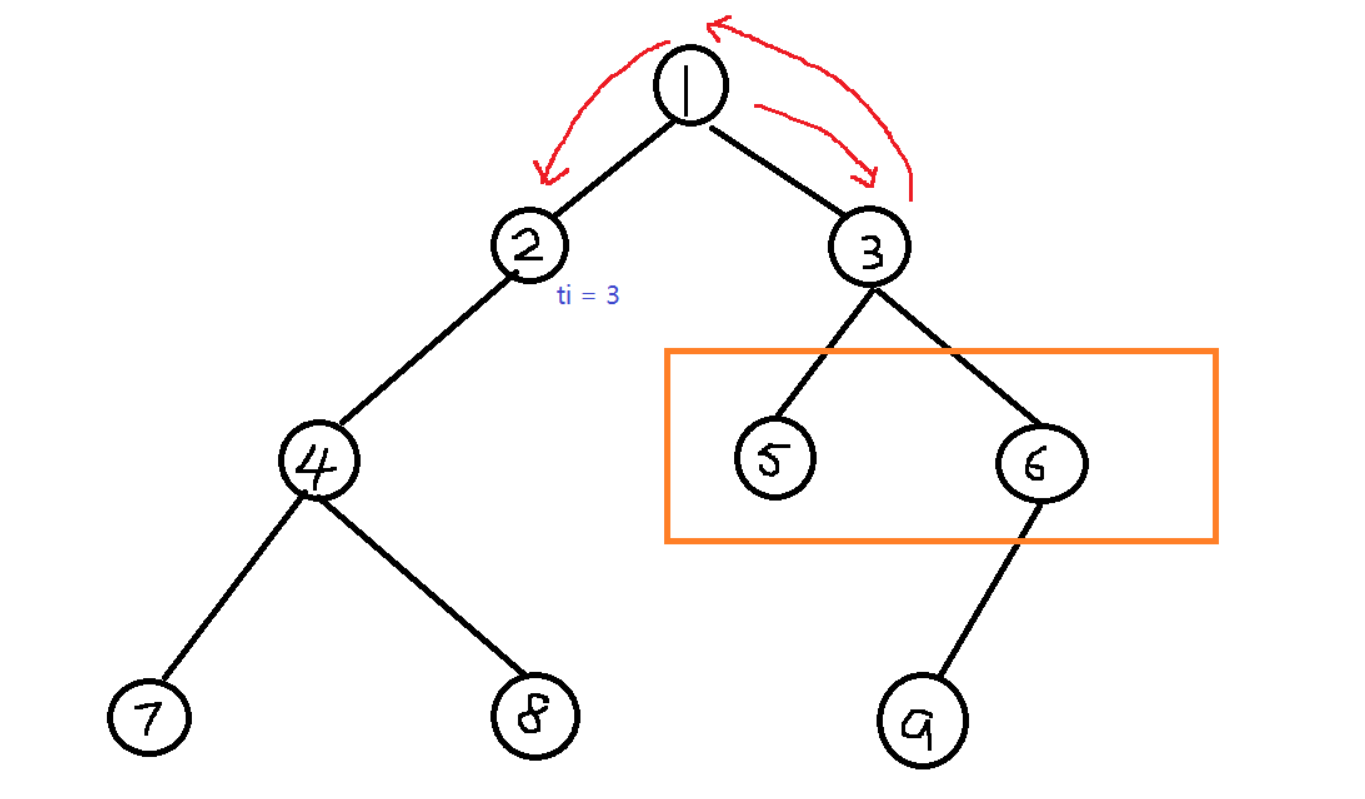
对于这棵树每个根就两种状态，就是绕还是不绕，可以先考虑不绕，不绕的话就是对于一个根来说根 + 儿子的max, 然后设dp方程，dp[i]代表第i个节点不包括i这个节点的最大权值，设1 <= j <= m为他的儿子，那么dp[i] = \(\sum\limits_{j = 1}^{j = m}\)dp[j] + max(a[j]), 这个就是转移过程，然后考虑绕的话，首先就是t[j] >= 3, 首先考虑那个来回的贡献，来回的贡献，就相当于那个贡献来回点的儿子全都是取不到的 - sum[j], sum[i]代表i儿子的下层的所有dp[j]的和，所以就是-dp[j] + sum[i] + a[j]这个就是这个来回点的贡献，还要加上那个t[i] == 3的那个点的a[i]，然后左右的取max, 然后这里有一个思想，如果已经选了一个点了，那接下来选的肯定是剩下的里面贡献最多的，所以这里可以先预处理出来，最后都取max

是在不懂看这个
题解

总结:
树上dp, 就是通过题目观察条件，然后写代码

点击查看代码

#include <bits/stdc++.h>
#define endl '\n'
#define IOS ios::sync_with_stdio(false);
using namespace std;

typedef long long ll;
const ll MAXN = 1e5 + 10;
ll T, n;
ll a[MAXN], t[MAXN], sum[MAXN], dp[MAXN];
vector<int> edge[MAXN];

void init()
{
	for (int i = 1; i <= n; ++i)
		sum[i] = 0, dp[i] = 0, edge[i].clear();
}

void dfs(int x, int fa)
{
	ll mx = 0;
	for (int i = 0; i < edge[x].size(); ++i)
	{
		int y = edge[x][i];
		if (y == fa)
			continue;
		dfs(y, x);
		mx = max(mx, a[y]);
		sum[x] += dp[y];
	}
	dp[x] = sum[x] + mx;
	if (edge[x].size() <= 1)	//叶子节点
		return;
	pair<int, int> amx[2];
	for (int i = 0; i < edge[x].size(); ++i)
	{
		int y = edge[x][i];
		if (y == fa)
			continue;
		int now = -dp[y] + sum[y] + a[y];
		if (now > amx[0].first)
			swap(amx[0], amx[1]), amx[0] = make_pair(now, y);
		else if (now > amx[1].first)
			amx[1] = make_pair(now, y);
	}
	for (int i = 0; i < edge[x].size(); ++i)
	{
		int y = edge[x][i];
		if (y == fa)
			continue;
		if (t[y] == 3 && amx[0].second == y)
			dp[x] = max(dp[x], sum[x] + a[y] + amx[1].first);
		else if (t[y] == 3)
			dp[x] = max(dp[x], sum[x] + a[y] + amx[0].first);
	}
}

int main()
{
	IOS; cin.tie(0), cout.tie(0);
	cin >> T;
	while (T--)
	{
		cin >> n;
		init();
		for (int i = 1; i <= n; ++i)
			cin >> a[i];
		for (int i = 1; i <= n; ++i)
			cin >> t[i];
		for (int i = 1, x, y; i <= n - 1; ++i)
			cin >> x >> y, edge[x].push_back(y), edge[y].push_back(x);
		dfs(1, 0);
		cout << dp[1] + a[1] << endl;
	}
	return 0;
}
/*
1
5
1 10 100 1000 10000
1 2 1 1 1
1 2
1 3
2 4
2 5
*/