Zero Path

传送门
题意：
一张二维图，每个坐标都只可能是1， -1，问是否可以从（1， 1）-> (n, m)，每次只能向右或者向下移动，是否可以到（n, m）点时路径总和为0，如果可以输出YES， 如果不可以输出NO

思路：
通过观察可以发现，经过的格子数量必然是n + m - 1, 所以n + m - 1为偶数时才有可能，所以n + m为偶数直接输出NO， 接下来不难想到dp求出从（1, 1）-> (n, m)的最大值和最小值，但是一般只能想到这里了，可以观察发现，min > 0或者max < 0是绝对不可能的，那只要考虑min <= 0 && 0 <= max的情况，考虑值的变动当然是在原先二维图中路径的变动，原先二维图中的路径变动，从一个改变一个格子的情况对值的影响有三种，-2，0，2，因为min和maxx必然是偶数，所以接下来的问题就是考虑min是否能够转移到max,如果可以转移，那么上面的式子就是YES的情况，考虑像这样的都可以进行斜向移动，那么就必然能够移动到max的路径，（任何路径都能够移动到），如果非要有严格的证明，那就一句话，每个格子都能在他的可以移动到的位置上进行选择，从而组合路径。
下面是更好的证明

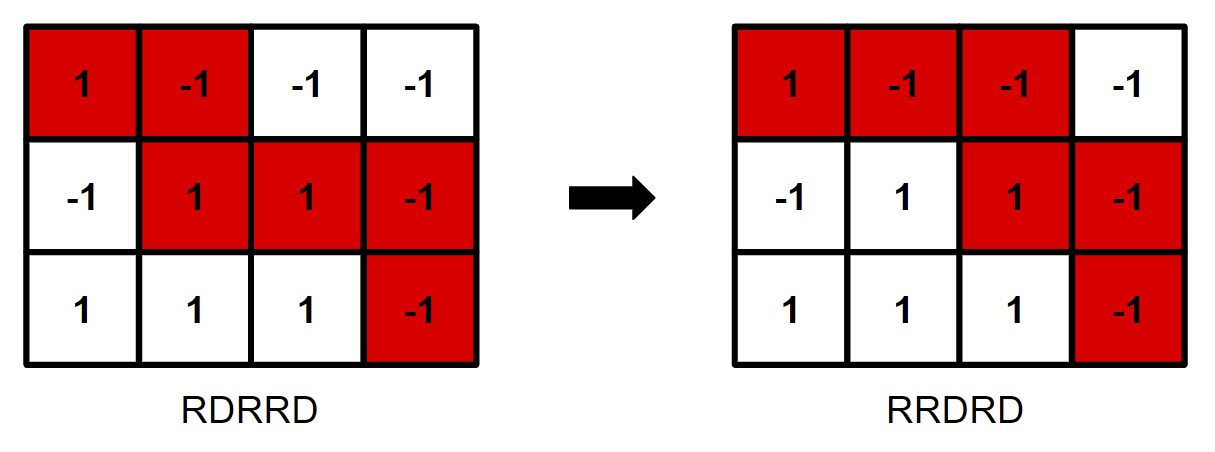
• 从最后一个字符往前推移，每一个点都只可能是从右或者上转移过来，如下图所示，可以将路径转换为一个字符串，那就考虑是否可以从左边的字符串变为右边的字符串，观察D的位置是可以进行左右移动的，所以左边的是可以变为右边的，证毕
  

点击查看代码

#include <bits/stdc++.h>
#define endl '\n'
#define IOS ios::sync_with_stdio(false);
using namespace std;

typedef long long ll;
const int N = 1e3 + 10;
int T, n, m;
int arr[N][N];
int dpmin[N][N], dpmax[N][N];

int main()
{
	//IOS; cin.tie(0), cout.tie(0);
    cin >> T;
    while (T--)
    {
        cin >> n >> m;
        for (int i = 1; i <= n; ++i)
        {
            for (int j = 1; j <= m; ++j)
            {
                cin >> arr[i][j];
            }
        }
        if ((n + m) % 2 == 0)   //因为他移动的格子数量肯定为 n + m - 1
        {
            cout << "NO" << endl;
            continue;
        }
        dpmin[1][1] = arr[1][1];
        dpmax[1][1] = arr[1][1];
        for (int i = 2; i <= m; ++i)    //先对第一行进行讨论
        {
            dpmin[1][i] = dpmin[1][i - 1] + arr[1][i];
            dpmax[1][i] = dpmax[1][i - 1] + arr[1][i];
        }
        for (int i = 2; i <= n; ++i)    //再对第一列进行讨论
        {
            dpmin[i][1] = dpmin[i - 1][1] + arr[i][1];
            dpmax[i][1] = dpmax[i - 1][1] + arr[i][1];
        }
        for (int i = 2; i <= n; ++i)    //对剩下的部分进行dp转移
        {
            for (int j = 2; j <= m; ++j)
            {
                dpmin[i][j] = min(dpmin[i - 1][j] + arr[i][j], dpmin[i][j - 1] + arr[i][j]);
                dpmax[i][j] = max(dpmax[i - 1][j] + arr[i][j], dpmax[i][j - 1] + arr[i][j]);
            }
        }
        //经过上述证明如果min <= 0 <= maxx, 就是ok
        if (dpmin[n][m] <= 0 && 0 <= dpmax[n][m])
        {
            cout << "YES" << endl;
        }
        else 
        {
            cout << "NO" << endl;
        }
    }
	return 0;
}