力扣练习——20 接雨水 II

1.问题描述

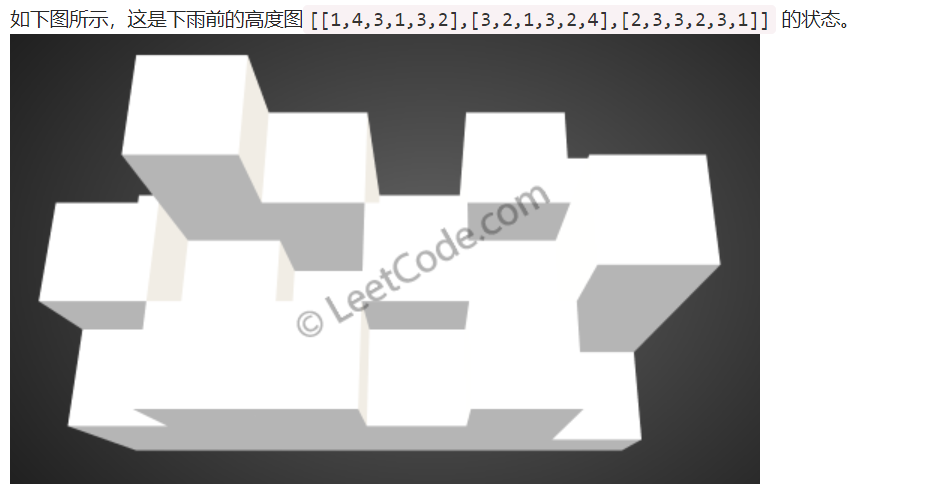
给你一个 m x n 的矩阵，其中的值均为非负整数，代表二维高度图每个单元的高度，请计算图中形状最多能接多少体积的雨水。

 

示例：

给出如下 3x6 的高度图:

[

  [1,4,3,1,3,2],

  [3,2,1,3,2,4],

  [2,3,3,2,3,1]

]

返回 4 。

 

 

 

 

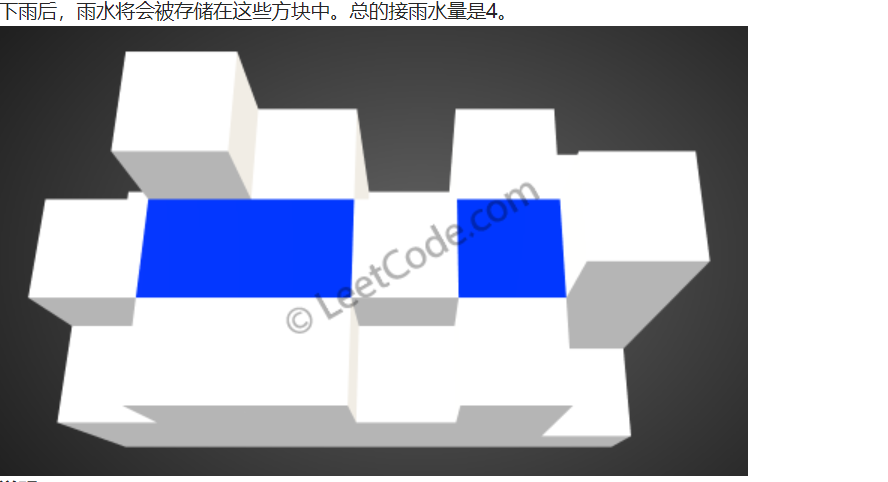
说明：

• 1 <= m, n <= 110

• 0 <= heightMap[i][j] <= 20000

 

可使用以下代码，完成其中的trapRainWater函数，其中形参heightMap为上述的二维高度图，返回接到的雨水量。

#include<iostream>

#include<stack>

#include<vector>

using namespace std;

 

class Solution {

public:

    int trapRainWater(vector<vector<int> >& heightMap)

    {

             //填充本函数完成功能  

    }

};

 

int main()

{

    int m, n,data;

    vector<vector<int> > heights;

    cin>>m>>n;

    for(int i=0; i<m; i++)

    {

        vector<int> row;

        for(int j=0; j<n; j++)

        {

            cin>>data;

            row.push_back(data);

        }

        heights.push_back(row);

    }

 

    int res=Solution().trapRainWater(heights);

    cout<<res<<endl;

    return 0;

}

 

2.输入说明 :

首先输入高度图的行列数m和n

然后输入m行，每行n个非负整数，表示heightMap的元素值，以空格分隔。

• 1 <= m, n <= 110

• 0 <= heightMap[i][j] <= 20000

 3.输出说明

输出一个整数，表示结果。

4.范例

输入

3 6
1 4 3 1 3 2
3 2 1 3 2 4
2 3 3 2 3 1

输出

4

5.代码

#include<iostream>

#include<stack>
#include<queue>
#include<vector>

using namespace std;



class Solution {

public:

    int trapRainWater(vector<vector<int> >& heightMap)

    {
        //木桶思想,参考题解https://leetcode.cn/problems/trapping-rain-water-ii/solution/jie-yu-shui-ii-by-leetcode-solution-vlj3/
        //1.特殊情况
        //heightMap.size()代表输入矩阵的行数，heightMap[0].size()代表列数；若最多只有两行或者两列，则都是四周最外层的方块，根本不可能接到雨水
        if (heightMap.size() <= 2 || heightMap[0].size() <= 2)
            return 0;
        //2.定义
        int m = heightMap.size();//行数
        int n = heightMap[0].size();//列数
        priority_queue<pair<int,int>, vector <pair<int,int>>, greater <pair<int,int>>>pq;//优先级队列
        //3.访问标记初始化
        //参考https://blog.csdn.net/BShanj/article/details/113817328
        vector<vector<bool>> visited(m, vector<bool>(n, false));
        //4.周边方块标记处理
        for (int i = 0; i < m; i++)
        {
            for (int j = 0; j < n; j++)
            {
                if (i == 0 || i == m - 1 || j == 0 || j == n - 1)
                {
                    visited[i][j] = true;
                    //最外层接水量water[i][j]=heightMap[i][j]
                    pq.push({ heightMap[i][j],i*n + j });//这里second存储的是该方块在以列排序中的位置，相当于从第一类第一个元素开始，往后以S型串成串
                }
            }
        }
        //5.处理中心部分
        //假设方块的索引为 (i,j)，方块的高度为heightMap[i][j]，方块接水后的高度为water[i][j]
        //方块 (i,j)(i,j) 的接水后的高度为：water[i][j]=max(heightMap[i][j],min(water[i-1][j],water[i][j-1],water[i+1][j],water[i][j+1]))
        int res = 0;
        int direction[]={ -1,0,1,0,-1 };//左，上，右，下四个方位
        while (!pq.empty())//非空时
        {
            pair<int, int> cur = pq.top();
            pq.pop();
            //遍历这个方块四周的水位高度
            for (int k = 0; k < 4; k++)
            {
                int nx = cur.second / n + direction[k];//注意，这里cur.second/n代表的是原方块的横坐标
                int ny = cur.second%n + direction[k + 1];//cur.second%n代表原方块的纵坐标
                if (nx >= 0 && nx < m&&ny >= 0 && ny < n && !visited[nx][ny])//这里要保证nx,ny均在正常范围内
                {
                    //当前方块的高度比周围的方块要高，容器内水的高度取决于最外层高度最低的方块
                    if (heightMap[nx][ny] < cur.first)//cur.first就是当前出队列的那个方块的高度heightMap[i][j]
                        res += cur.first - heightMap[nx][ny];//方块（i,j）实际接水量为water[i][j]-heightMap[i][j]
                    visited[nx][ny] = true;
                    pq.push({ max(heightMap[nx][ny], cur.first), nx * n + ny });
                }
            }
        }

        return res;

    }

};



int main()

{

    int m, n, data;

    vector<vector<int> > heights;

    cin >> m >> n;

    for (int i = 0; i < m; i++)

    {

        vector<int> row;

        for (int j = 0; j < n; j++)

        {

            cin >> data;

            row.push_back(data);

        }

        heights.push_back(row);

    }



    int res = Solution().trapRainWater(heights);

    cout << res << endl;

    return 0;

}