小波分析与应用--听课笔记 Lecture 3(18)
连续小波变换
连续小波变换的定义
- 小波 Wavelet
设\(f(t)\in L^{2}(R),\psi(t)\in L^{2}(R)\)为小波函数,\(f(t)\)为连续小波变换,定义为\(Wf(u,s)=\left \langle f,\psi_{u,s} \right \rangle=\int_{-\infty}^{+\infty}f(t)\frac{1}{\sqrt{s}}\psi * (\frac{t-u}{s})dt,u\in R^{1},s>0\)
- Maxican hat
\(\psi(t)=\frac{2}{\sqrt{3}}\pi^{-\frac{1}{4}}(1-t^{2})e^{-\frac{t^{2}}{2}}\)
频域\(\hat{\psi}(\omega)=\frac{\sqrt{8}\pi^{\frac{1}{4}}}{\sqrt{3}}\omega^{2}e^{-\frac{\omega^{2}}{2}}\)
- 小波变换的时频字典
对小波\(\psi(t)\)进行伸缩和平移,可得到一簇小波函数,这就是连续小波变换的时频字典。
\(D=\left \{ \psi_{u,t}(t)=\frac{1}{\sqrt{s}}\psi(\frac{t-u}{s}) \big| u\in R,s>0 \right \}\)
其中,\(s\)为尺度或者伸缩参数,\(u\)为平移参数。系数\(\frac{1}{\sqrt{s}}\)保证\(\psi_{u,s}(t)\)与\(\psi(t)\)具有相同的能量,即\(\left \| \psi_{u,s}(t) \right \|^{2}=\left \| \psi(t) \right \|^{2}\) - \(\psi_{u,s}(t)\)视频窗口的可调节性。
连续小波变换的物理解释--从信号处理的观点
对任意给定的参数\(s>0\),令
\(\bar{\psi}_ {s}(t)=\frac{1}{\sqrt{s}}\psi^{* }(-\frac{t}{s})\)
则连续小波变换可以重写如下卷积形式
\(Wf(u,s)=f*\bar{\psi}_ {s}(u)\)
假定\(\psi(t)\)的频率中心为\(\omega^{* }\),带宽为\(\sigma_{\omega}\)。根据\(\hat{\bar{\psi}}_ {s}(\omega)=\sqrt{s}\hat{\psi}^{* }(s\omega)\)知,\(\bar{\psi}_ {s}(t)\)的频率中心为\(\frac{\omega^{* }}{s}\),带宽为\(\frac{\sigma_{\omega}}{s}\)
时频窗特点
\(\psi(t): (0,\omega^{* })\)
\(\psi_{u,s}(t):u,\frac{\omega^{* }}{s},s\sigma_{t},\sigma_{* }/s\)
时频窗口的特点,适用两种
- 信号中的快变成分(例如,陡峭的前沿和后沿、尖脉冲和瞬态信号等)
这类成分属于宽带高频成分。对这种信号分析,一般要求时间分辨率高,以适应快变成分时间间隔短的要求,对频率分辨率可以适当放宽。因此,需要很少用位于时频平面高端的时宽窄而带宽打的分析窗。 - 信号中慢变成分
这类成分属于窄带低频成分。对于这类信号的分析,一般要求频率的分辨率高,而时间的分辨率可以放宽。因此,需要使用位于时频平面低端的时宽大而带宽窄的分析窗。
时频窗口的恒Q性质
设\(\psi(t)\)为小波函数,它的频率中心和带宽分别为\(\omega^{* },\sigma_{\omega}\),则\(\psi(t)\)的品质因子Q定义为
\(Q=\frac{\omega^{* }}{\sigma_{\omega}}\)
- 实际应用中小波Q因子的选择
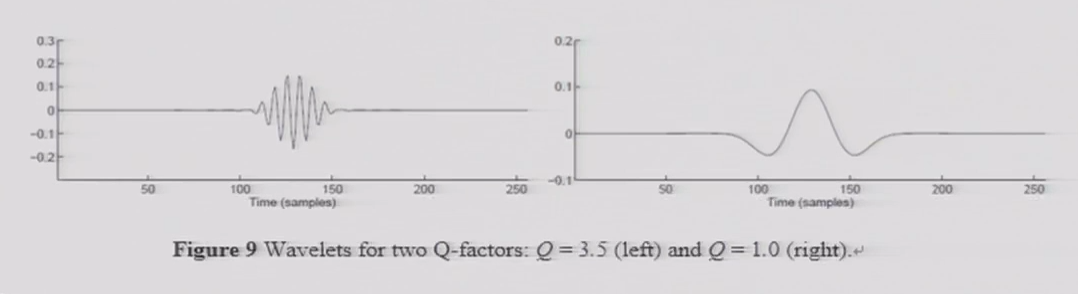
小波函数\(\psi(t)\)的Q因子控制着它的震荡性能
- 低Q因子小波
For low Q-filter, the wavelet has few sign changes and consists of few oscillatory cycles.因此,低Q因子的小波变换可以有效的表示分段光滑信号,如图像等。 - 高Q因子小波
For higher Q-factor, the wavelet has more sign changes and consists of more osillatory cycles. 因此,高Q因子的小波变换可以有效的表示震荡信号,如音频信号、机械震荡信号、地震勘探信号和EEG信号。
I. W. Selesnick, Wavelet transform with tunable Q-factor, IEEE Trans Signal Processing, vol. 59, no. 8, 3560-3575, 2011
J. Youngberg and S. Boll, Constant-Q signal analysis and synthesis
小波变换反变换存在条件
解析小波\(\hat{\psi}(w)=0,w<0\)
几种常见的小波
1 Mexican hat
Gaussian 函数的二阶导数,具有非常好的时频聚集性能,它的规范化时域和频域表示如下。
\(\psi(t)=\frac{2}{\sqrt{3\sigma}\pi^{\frac{1}{4}}}(1-\frac{t^{2}}{\sigma^{2}})e^{-\frac{t^{2}}{2\sigma^{2}}}\)
\(\hat{\psi}(\omega)=\frac{\sqrt{8}\sigma^{5/2}\pi^{1/4}}{\sqrt{3}}\omega^{2}e^{-\frac{\sigma^{2}\omega^{2}}{2}}\)
注:小波函数的一般定义为
\(\int_{-\infty}^{+\infty}\psi(t)dt=0\)
任取一个函数\(g(t) \xrightarrow[]{t\rightarrow \pm \infty}0\)
则\(\psi(t)={g}'(t)\)为小波函数
以Gaussian函数为例
在地震勘探领域,Mexican小波也称为Ricker子波,常用如下形式表示
\(\psi(t)=\left ( 1-2(\pi f_{M}t)^{2} \right )e^{-(\pi f_{M} t)^{2}}\)
\(\hat{\psi}(f)=\frac{2}{\sqrt{\pi}}\frac{f^{2}}{f_{M}^{3}}e^{-\frac{f^{2}}{f_{M}^{2}}}\)
其中\(f_{M}\)为峰值频率,它是一个可调参数。
\(\left \| f \right \|^{2}= \frac{1}{C_{\psi}}\int_{0}^{+\infty}\int_{-\infty}^{+\infty}\left | \frac{Wf(u,s)}{s} \right |^{2}duds\)
时间尺度平面上,\(P_{\omega}f(u,s)=\left|Wf(u,s) \right|^{2}\)
尺度图
- 尺度图--在时间尺度平面上
对任意\(f(t)\in L^{2}(R)\),\(f(t)\)的尺度图定义上
\(P_{W}f(u,s)=\left | Wf(u,s) \right |^{2}=\left | \int_{\infty}^{+\infty}f(t)\frac{1}{\sqrt{s}}\psi*(\frac{t-u}{s})dt \right |^{2}\)
根据连续小波变换的能量保持公式,\(P_{W}f(u,s)\)可以视为信号\(f(t)\)的能量在时间尺度上的分布。 - 小波谱图--在时频平面上
设\(\psi(t)\)在时频中心为\((0,\omega^{* })\),则\(\psi_{u,s}(t)\)的视频中心为\((u,\frac{\omega^{* }}{s})\)。由于\(Wf(u,s)=\left \langle f(t),\psi_{u,s}(t) \right \rangle\)的值度量了信号\(f(t)\)在时频平面上以\((u,\frac{\omega^{* }}{s})\)为中心的时频窗口。
\(\left [ u-\frac{s\sigma_{t}}{2}, u+\frac{s\sigma_{t}}{2} \right ]\times\left [ \frac{\omega^{*}}{s} -\frac{\sigma_{\omega}}{2s},\frac{\omega^{*}}{s} +\frac{\sigma_{\omega}}{2s}\right ]\)
内的信息,故\(Wf(u,s)\)可以视为信号\(f(t)\)在时间\(u\)附近含有频率\(\omega= \frac{\omega^{* }}{s}\)多少的度量。因此,在时频平面上,小波谱图可以表示为
\(P_{W}(u,\omega)=\left | Wf(u,\frac{\omega^{* }}{s}) \right |^2\)
信号分类
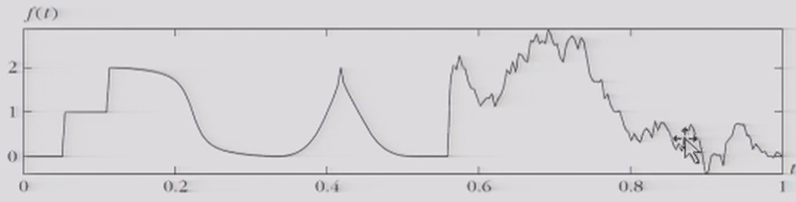
分段光滑信号+分形信号(奇异点连续存在)
小波适合分段光滑信号
多分量信号:\(f(t)=\sum_{k=1}^{K}A_{k}(t)\cos \phi_{k}(t)\)
\(f(t)\)的离散化:\(f[n]=f(nT),0\leq n<2^{10}\),采样周期\(T=2^{-10}\)
尺度参数\(s\)的离散化:\(s_{l} = (\sqrt[n_{v}]{2})^{l}\),\(n_{v}=32 \ or \ 64\),\(2^{-6}\leq s_{l}\leq 2^{0}=1\)
解析小波
对实信号,使用解析小波变换主要有下面三种原因:
- 实信号的频谱是共轭对称的,因此,正频包含了信号的所有信息。
- 可以出去时频平面上正负频率成分之间的交叉干扰。特别的,可以避免时频平面上负频成分的信息向正频泄露。
- 解析小波变换是多分量震荡信号\(f(t)=\sum_{k=1}^{K}A_{k}(t)\cos \phi_{k}(t)\)分析和处理最重要的工具之一。例如,人们可以从解析小波变换的模的极大值点的处信息,回复信号\(f(t)\)的瞬时振幅\(A_{k}(t)\)和瞬时频率\({\phi}'_ {k}(t)\)等瞬时属性。
解析信号
解析函数\(\hat{f}(w)=0,w<0\)。解析小波\(\hat{\phi}(w)=0,w\leq 0\),\(\phi(t)\)为复小波
定义 设\(f(t)\in L^{2}(R)\),如果\(\hat{f}(w)=0,w<0\),则称\(f(t)\)为解析信号。由于实信号的Fourier变换是共轭对称的,因此解析信号一定是复信号。
实信号的解析化
实信号的解析化是震荡信号分析与处理的重要工具之一。实信号通过解析化,可以用于提取它的瞬时振幅\(A(t)\),瞬时相位\(\phi(t)\)和瞬时频率\({\phi}'(t)\)
对任意实信号\(f(t)\in L^{2}(R)\),令
\(\hat{f}_{a}(w)=\left\{\begin{matrix}
2\hat{f}(w) & {\rm if}\ w\geq 0\\
0 & {\rm if}\ w< 0
\end{matrix}\right.\)
称\(\hat{f}_ {a}(w)\)为实信号\(f(t)\)对应的解析信号。
解析信号\(\hat{f}_ {a}(w)\)一个等价的表示为

 浙公网安备 33010602011771号
浙公网安备 33010602011771号