小波分析与应用--听课笔记 Lecture 1

Lecture 1

信号的表示

信息的物理载体就是信号。信号处理领域的一个永恒的主题是构造寻找信号的简洁的具有物理可解释的主题。小波变换对非平稳信号，提供一种表示方式。

什么是小波 wavelet

\(\psi (t) \in L^{2}(R)\) 模值平方小于无穷大（能量有限）\(\int_{R}\psi(t)dt = 0\)
实际应用中，要求在时域和频域，\(\psi(t) \ \hat{\psi}(w)\)快速衰减

原始动机

信号处理领域，一个永恒的主题，就是要寻求信号的简洁的具有物理可解释的表示方法。这样就可以在变换域中，挖掘信号的各种信息。本质是，小波变换也是一种表示形式。用简单的小波基，通过伸缩平移变换，构成\(L^{2}\)空间的标准正交基。信号在标准正交基下，具有稀疏性的表达（很少的基本元素，将信号表示出来）。从复杂信号，挖掘特征信息。

1. 正交小波基的构造。
   • 1910，Harr小波正交基。（简洁，具有物理意义）
     \(\psi(t)=\left\{\begin{matrix} 1, & 0\leq t<\frac{1}{2}\\ -1,& \frac{1}{2}\leq t< 1 \\ 0 &0 \end{matrix}\right.\)
     伸缩与平移
     \(\{\psi_{j,n}(t)=2^{-\frac{j}{2}} \psi(2^{-j}t-n), j,n\in Z \}\)构成了\(L^{2}(R)\)标准正交基
   • 光滑正交小波基，Meyer，Mallet：建立多分辨分析，正交小波基构建方法
2. 连续小波变换
   信号变换有两种基本思路，一种是在正交基下，提供信号表示；第二种，通过把信号做变换，通过核函数的积分变化，把信号变换到核函数的域中去。1984，Morlet，\(\forall f(t)\in L^{2}(R)\),
   \(W_{f(u,s)}= \int_{R} f(t)\frac{1}{\sqrt{s}}\psi(\frac{t-u}{s})\)
   \(f(t)\rightarrow W_{f(u,s)}\)
3. 小波为什么有用
   • 稀疏表示：正交基-压缩，去噪，特征提取等。
   • 检测小尺度信号：连续小波变换。引力波（检测放大小信号），奇异性（故障诊断）等。

Lecture 2 第一章 稀疏表示

信号的表示

当今人们生活在一个信息时代，而信息的物理载体就是信号。在我们身边及我们身上，信号是无处不在的，我们通过信号获取信息，信号在我们的生活中扮演着及其重要的作用。例如，人们随时可以听到的语音信号和机械信号，随时可以看到的图像信号，以及生命体存在的心电、脑电、脉搏、心压、呼吸等众多生理信号。为了对信号进行分析和处理，我们必须建立信号各种不同的表示。信号处理技术已经成为我们分析和理解物理世界的重要工具。

1. 信号的时域表示
   一维表示：\(f(t)\)；通过对连续采样，离散形式\(f[n]\)
   二维函数：\(f(x,y)\)二维函数采样，变成矩阵\(\left( f(i,j)\right ) _ {m\times n}\)在信号处理领域，一个永恒的主题是：寻找信号简洁的且在物理上可解释的变换域表示。

2. 信号的频域表示
   时间和频率是描述信号的两个基本物理量。信号\(f(t)\)通过Fourier变换可以得到它的频域表示\(\hat{f}(w)\)，并且通过逆变换也可以把信号表示成不同频率正弦波的叠加。
   \(f(t)\in L^{2}(R)\)，能量空间，能量有限的L2空间。
   \(\hat{f}(w)=\int_{R} f(t)e^{-jwt}dt = \left \langle f(t),e^{jwt} \right \rangle\) 内积，物理意义是，该信号含相应频率信号的量。为了不丢失，傅里叶变换，存在相应的反变换。
   \(f(t)=\frac{1}{2\pi}\int_{R}\hat{f}(w)e^{jwt}dt\)

   • 离散傅里叶变换
     \(w_{K}=\frac{w\pi K}{N}\),长度为N的离散信号，\(O(N\log_{2}N)\)
     Example
     \(f(t)=\sin(100\pi t)+ \sin(600\pi t) + n(t), 0\leq t\leq 1\), \(n(t) \sim N(0,\sigma^{2})\)为高斯白噪声
     傅里叶变换问题：只适用于平稳信号
     对于非平稳信号，人们希望知道的是某一特定时刻或者某一很短的时间范围，该信号所对应的频率是多少，也就是人们需要用时变的频谱来刻画它。因此，人们需要用时间和频率的联合函数来表示信号，这就是信号的时频表示。经典的时频分析方法：短时傅里叶变换，小波变换和二次时频分布等。
     第一类，线性时频分析，就是用核函数/内积，用核函数去量：短时傅里叶变换和小波变换。
     第二类，二次时频分布，Wigner分布。等。
     短时（窗口）傅里叶变换
     \(S(f(u,\xi ))= \int_{-\infty }^{+\infty}f(t)g(t-u)e^{-j\xi t}dt=\left \langle f(t)g(t-u),e^{j\xi t} \right \rangle=\left \langle f(t),g(t-u)e^{j\xi t} \right \rangle\)，其中\(g_{u,\xi}(t)=g(t-u)e^{j\xi t}\)
     其逆变换为\(f(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}Sf(u,\xi)g(t-u)e^{j\xi t}dud\xi\)
     离散STFT（short time Fourier transformation）\(O(N^{2}\log_{2}N)\)
     \(\left | Sf(u,\xi) \right |^{2}\) \(\rightarrow\) 谱图
     \(S(f(u,\xi ))=\left \langle f(t),g(t-u)e^{j\xi t} \right \rangle\)，以\(g(t)\)为高斯函数为例，其傅里叶变换\(\hat{g}(w)\)也是高斯函数。
   • 小波变换
     \(Wf(u,s)=\left \langle f(t),\psi_{u,\xi}(t) \right \rangle=\int_{R^{1}}f(t)\frac{1}{\sqrt{s}}\psi^{* }\left(\frac{t-u}{s} \right)dt\)

信号的稀疏表示

在信号处理领域，另一个永恒的思想是：将信号分解成简单波形的线性组合，并且寻找简洁的信号表示。这样做可以去除信号中的冗余性，有助于我们了解信号的性质，提取有用的信息，以便于进一步对信号进行分析和处理。

1. 信号在基集下的表示
   设\(H\) 为Hilbert空间，\(\left \{ \phi_{\gamma} \right \}_ {\gamma \in\Gamma }\subset H\), \(\Gamma\)为有限或可数指标集。

• \(\left \{ \phi_{\gamma} \right \}_ {\gamma \in\Gamma }\) 是冗余基（字典）：
  \(\overline{span}\{ \phi_{\gamma}| \gamma \in \Gamma \}=H\),且\(\left \{ \phi_{\gamma} \right \}_ {\gamma \in\Gamma }\)线性相关。
  这时，任意信号\(f\in H\)可表示为
  \(f=\mathop{\sum}\limits_{\gamma \in \Gamma}c_{\gamma}\phi_{\gamma}\),且表示系数\(\left\{ c_{\gamma} \right\} _ {\gamma \in \Gamma}\)并不是唯一的。
• \(\left\{ c_{\gamma} \right\} _ {\gamma \in \Gamma}\)是基
  \(\overline{span}\{ \phi_{\gamma}| \gamma \in \Gamma \}=H\),且\(\left \{ \phi_{\gamma} \right \}_ {\gamma \in\Gamma }\)线性无关。
  这时，任意信号\(f\in H\)可表示为
  \(f=\mathop{\sum}\limits_{\gamma \in \Gamma}c_{\gamma}\phi_{\gamma}\),且表示系数\(\left\{ c_{\gamma} \right\} _ {\gamma \in \Gamma}\)是唯一的。
• \(\left\{ c_{\gamma} \right\} _ {\gamma \in \Gamma}\)是标准正交基
  \(\overline{span}\{ \phi_{\gamma}| \gamma \in \Gamma \}=H\)，且\(\left \langle \phi_{\gamma},\phi_{\gamma^{'}} \right \rangle=\left\{\begin{matrix} 1 &\gamma = \gamma^{'} \\ 0& \gamma \neq \gamma^{'} \end{matrix}\right.\)
  这时，任意信号\(f\in H\)可以表示为
  \(f=\mathop{\sum}_ {\gamma\in\Gamma}\left \langle f,\phi_{\gamma} \right \rangle\phi_{\gamma}\)
• Remark
  从数学上讲，正交基是Hilbert空间中最理想的基集。它通常在数学上更容易被处理，具有很多优良的性质。
  对于冗余的基集（字典），信号有无穷多种表示。正是这种表示的不唯一性，为我们的选择合适的表示提供了极大的灵活性。其中，一种具有及其重要意义的表示是：稀疏表示。
  信号的稀疏表示
  设\(H\)为Hilbert空间，\(f\in H\)，\(\{ \phi_{\gamma} \}_ {\gamma\in \Gamma} \subset H\)为一组基集，如果\(f\)可用\(\{ \phi_{\gamma} \}_ {\gamma\in \Gamma}\)中很少的基元\(\phi_{\gamma}\)表示或近似表示，则称这种表示为\(f\)的稀疏表示。
  正交小波基之所以有用，一个非常重要的原因就是，它可以为相当广泛的一类信号提供稀疏表示。正交小波基这种重要性质，将在接下来给出直观解释。
  同时需要指出，不存在一个通用的基集，为所有的信号提供稀疏表示。正如Mallat所说：寻找为所有信号提供理想稀疏表示的“圣杯”是一个无望的追求。
  Remark：设计为具体信号提供稀疏表示的基集，并且构造相应的快速分解与重构算法，一直是信号处理领域中研究的热点问题。

Lecture 4 正交小波基

1. 正交小波基
   小波理论研究的核心问题之一是：构造满足一定性能的小波函数\(\psi(t\)，使其经过二进制伸缩和平移后所生成的小波簇
   \(\left \{ \Psi_{j,n}(t)=2^{-\frac{j}{2}}\Psi(2^{-j}t-n)|j,n\in Z \right \}\)构成\(L^{2}\)空间中的标准正交基。
   这时，对于任意\(f(t)\in L^{2}\)，有
   \(f(t)=\mathop{\sum}_{j,n\in Z}\left \langle f,\psi_{j,n} \right \rangle \psi_{j,n}(t)\)并且称\(\left \langle f,\psi_{j,n} \right \rangle = \int_{-\infty}^{+\infty}f(t)\psi_{j,n}(t)dt\)为正交小波变换,\(\psi(t)\)为正交小波。
2. 正交小波基下稀疏表示的例子
   已经证明：正交小波基\(\left \{ \psi_{j,n}(t)|j,n\in Z \right \}\)可为分段光滑信号提供稀疏表示。
   例一 分段光滑信号
   
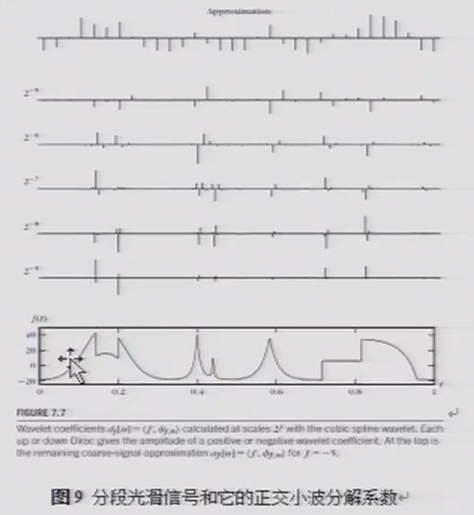
   考虑定义在\([0,1]\)上的连续信号\(f(t)\)，它的采样信号为
   \(f[k] = f(2^{-10}k),0\leq \<N=2^{10}\)，采样周期\(T=2^{-10}\)
   图中给出了信号\(f\)的5层
3. Haar小波
   Haar小波是分段常数函数 \(\psi(t)=\left\{\begin{matrix} 1, & 0\leq t<\frac{1}{2}\\ -1,& \frac{1}{2}\leq t< 1 \\ 0 &0 \end{matrix}\right.\)
   它的二进制伸缩与平移\(\left \{ \psi_{j,n}(t)=2^{\frac{-j}{2}}\psi(2^{-j}t-n) \right \}\)构成\(L^{2}(R)\)中的标准正交基

• Haar小波性质
  Haar小波之所以能为分段光滑信号提供稀疏表示，一下两个性质
  均值为零 \(\int_{-\infty}^{+\infty}\psi(t)dt=0\)从而\(\int_{-\infty}^{+\infty}\psi_{j,n}(t)dt=0\)
  有限支撑(紧支撑)\(\psi_{j,n}(t)\)支撑为\(\left[2^{j}n,2^{j}(n+1)\right)\)

4. 二维小波变换
   一维正交小波基：\(\psi(t)\),高通滤波器，\(\phi(t)\)低通滤波器,尺度函数
   二维构造\(L^{2}(R^{2})\):\(\begin{cases} \psi^{1}(\vec{x})=\phi(x_{1})\psi(x_{2}) & \text{vertical} \\ \psi^{2}(\vec{x})=\phi(x_{2})\psi(x_{1}) & \text{ herizontal} \\ \psi^{3}(\vec{x})=\psi(x_{1})\psi(x_{2}) & \text{ diagonal } \end{cases}\)
   \(\left \{ \psi_{j,\vec{n}}^{k}(\vec{x})=2^{-j}\psi^{k}(2^{-j}\vec{x}-\vec{n}),1\leq k\leq3,\vec{n}\in Z^{2},j\in Z \right \}\)
   构成\(L^{2}(R^{2})\)标准正交基
5. 正交小波变换最成功的的两个应用--压缩与去噪

• compression
  信号在一组基下的稀疏表示是压缩编码的理论基础
  设离散信号\(f[n],0\leq n<N\),\(\left\{g_{m}\right\}_ {m=1}^{N}\subset C^{N}\)为正交小波基，有
  \(f=\mathop{\sum}_{m=1}^{N}\left \langle f,g_{m} \right \rangle g_{m}\)
  压缩：保留幅值较大的洗漱，其余系数置零，即保留系数
  \(\left \{ \left \langle f,g_{m} \right \rangle \Big| |\left \langle f,g_{m} \right \rangle|\geq T,0\leq n<N \right \}\),其中\(T>0\)成为阈值或者门限。
  恢复重构\(\widetilde{f}=\mathop{\sum}_{|\left \langle f,g_{m} \right \rangle| \geq T}\left \langle f,g_{m} \right \rangle g_{m}\)
  重构误差（失真率）\(\left \| \tilde{f}-f \right \|^{2} \Big/ \left \| f \right \|^{2}\)
  由于\(\left \{ g_{m} \right \}_ {m=1}^{N}\)为标准正交基，故
  \(\frac{\left \| \tilde{f}-f \right \|^{2}}{\left \| f \right \|^{2}}=\frac{\mathop{\sum}_{|\left \langle f,g_{m} \right \rangle| < T} \left | \left \langle f,g_{m} \right \rangle \right |^{2} }{\mathop{\sum} _{m=1}^{N} \left | \left \langle f,g_{m} \right \rangle \right |^{2}}\)
  从上述表示可以看出，如果信号的能量主要集中在少数的高幅值小波系数上，则除去相对较小的小波系数后，仍然可以获得高质量的重构信号。
  Remark 用于图像压缩编码的国际标注JPEG2000,就是基于二维正交小波变换的图像压缩编码。
• denoising 去噪
  定量刻画重构信号\(\tilde{f}\)的质量，一个广泛使用的标准是重构信噪比
  \(SNR=10\log_{10}\frac{\left \| f \right \|^{2}}{\left \|\tilde{f}- f \right \|^{2}}=20\log_{10}\frac{\left \| f \right \|}{\left \|\tilde{f}- f \right \|}\text{dB}\)

6. 在冗余基（字典）下表示
   \(\left \{ \phi_{p} \right \}_ {p\in P} \subset H\) 冗余\(\forall f \in H\)
   \(f=\mathop{\sum}_{p\in P} c_{p}\phi_{p}\)无穷多个
   选取\(\{c_{p}\}\)稀疏表示，极小化\(l^{2}\)范数：\(\arg \min \mathop{\sum}_{p\in P}|c_{p}|^{2}\)

• 框架
  标准正交基的推广
  \(\left \{ \phi_{p} \right \} _ {p\in P} \subset H\)。保能（能量）是标准正交基的充分必要条件。
  \(\left \| f \right \|^{2}=\mathop{\sum}_{p\in P} \left | \left \langle f,\phi_{p} \right \rangle \right |^{2},\forall f\in H\)
  框架可视为正交基概念的推广。框架的理论提供了在冗余基下，求解信号表示系数具有极小化\(l^{2}\)范数的方法
  定义 设\(H\)为Hilbert空间，称\(\{ \phi_{p} \}_ {p\in \Gamma } \subset H\)为H中的框架，如果存在常数\(0<A\leq B<+\infty\)
  使得\(A\left \|f \right \|^{2}\leq \mathop{\sum}_{p\in \Gamma}\left |\left \langle f,\phi_{p} \right \rangle \right |^{2}\leq B\left \|f \right \|^{2},\ \forall f\in H\)
  特别的，当\(A=B\)时，称\(\{ \phi_{p} \}_ {p\in \Gamma }\)为紧框架。
• 求解冗余基下稀疏表示的经典算法，匹配追踪和基追踪
  面临两个问题，首先构造匹配基 \(\{\phi_{p} \}_ {p\in P}\) 第二个问题，如何表示，构造及快速算法
  匹配追踪
  Algorithm，设\(H\)为Hilbert空间，\(\{ \phi_{p} \}_ {p\in \Gamma } \subset H\)为字典，且\(\left \| \phi_{p} \right \|=1\)。任取\(f\in H\)，则求解\(f\)在该字典下的稀疏表示的匹配追踪算法表示如下：
  令\(\phi_{p_{0}}=\mathop{\arg\max}_ {p\in \Gamma} \left | \left \langle f,\phi_{p} \right \rangle \right |\)
  基追踪 Basic pursuit(BP)

7. 反问题
   信号\(f\rightarrow\)系统\(\rightarrow g\)观测信号。根据系统，和观测信号\(g\)求信号\(f\)。
   一般模型
   \(Y=Uf+W\)
   难点：\(U^{-1} \exists\)，无界，数值不稳定。\(Q<N\)无穷多个解
   \(\min \frac{1}{2}||Y-Uf||^{2}\),光滑条件\(\min||f||^{2}\)。将两个条件合并
   \(\min \frac{1}{2}||Y-Uf||^{2}+\lambda\min||f||^{2}\)
   稀疏性方法：
   \(\min \frac{1}{2}||Y-Uf||^{2}+\lambda||f||_ {l^{1}}\)
   压缩采样

可以\(y\)建模
\(\boldsymbol y = \Phi_ {m\times n} \boldsymbol x\)
其中\(\Phi_ {m\times n}\)是采样矩阵\(m\ll n\)，\(\boldsymbol y\in R^{m}\)为压缩采样信号，\(\boldsymbol x \in R^{n}\)为原信号
信号恢复
压缩传感理论最核心的问题之一是：由于\(m\ll n\)，故方程组\(\boldsymbol y = \Phi_ {m\times n} \boldsymbol x\)有无穷多解。因此，想要从采样信号\(\boldsymbol y\)恢复原信号\(\boldsymbol x\)，必须对方程组\(\boldsymbol y = \Phi_ {m\times n} \boldsymbol x\)的解增加约束条件。这就是：信号\(\boldsymbol x\)是稀疏的。因此，信号恢复问题，可以建模为方程组\(\boldsymbol y = \Phi_ {m\times n} \boldsymbol x\)最稀疏解的问题。
即

\[\min ||\boldsymbol x||, {\rm st} \ \boldsymbol y = \Phi_ {m\times n} \boldsymbol x \]

基本问题
采样矩阵\(\Phi\)的构造
满足RIP采样条件矩阵构造：随机高斯矩阵，随机\(\pm1\)矩阵
抽取正交Fourier变换矩阵等。
重构算法设计\(l^{0},l^{1}\)极小化算法和贪婪算法等