强化学习 6 ——价值函数逼近

上篇文章强化学习——时序差分 (TD) 控制算法 Sarsa 和 Q-Learning我们主要介绍了 Sarsa 和 Q-Learning 两种时序差分控制算法，在这两种算法内部都要维护一张 Q 表格，对于小型的强化学习问题是非常灵活高效的。但是在状态和可选动作非常多的问题中，这张Q表格就变得异常巨大，甚至超出内存，而且查找效率极其低下，从而限制了时序差分的应用场景。近些年来，随着神经网络的兴起，基于深度学习的强化学习称为了主流，也就是深度强化学习（DRL）。

一、函数逼近介绍

我们知道限制 Sarsa 和 Q-Learning 的应用场景原因是需要维护一张巨大的 Q 表格，那么我们能不能用其他的方式来代替 Q表格呢？很自然的，就想到了函数。

\[\hat{v}(s, w) \approx v_\pi(s) \\ \hat{q}(s,a, w) \approx q_\pi(s, a) \\ \hat{\pi}{a,s,w} \approx \pi(a|s) \]

也就是说我们可以用一个函数来代替 Q 表格，不断更新 \(q(s,a)\) 的过程就可以转化为用参数来拟合逼近真实 q 值的过程。这样学习的过程不是更新 Q 表格，而是更新 参数 w 的过程。

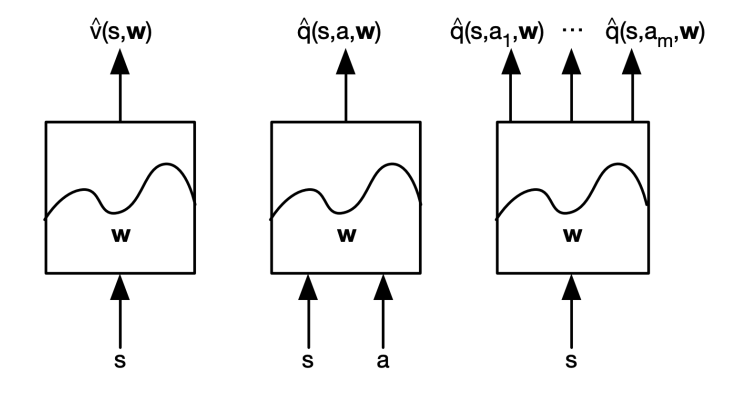
下面是几种不同的拟合方式：

第一种函数接受当前的 状态 S 作为输入，输出拟合后的价值函数

第二种函数同时接受 状态 S 和 动作 a 作为输入，输出拟合后的动作价值函数

第三种函数接受状态 S，输出每个动作对应的动作价值函数 q

常见逼近函数有线性特征组合方式、神经网络、决策树、最近邻等，在这里我们只讨论可微分的拟合函数：线性特征组合和神经网络两种方式。

1、知道真实 V 的函数逼近

对于给定的一个状态 S 我们假定我们知道真实的 \(v_\pi(s)\) ，然后我们经过拟合得到 \(\hat{v}(s, w)\) ，于是我们就可以使用均方差来计算损失

\[J(w) = E_\pi[(v_\pi(s) - \hat{v}(s, w))^2] \]

利用梯度下降去找到局部最小值：

\[\Delta w = -\frac{1}{2}\alpha \nabla_wJ(w) \\ w_{t+1} = w_t + \Delta w \]

我们可以提取一些特征向量来表示当前的 状态 S，比如对于 gym 的 CartPole 环境，我们可提取的特征有推车的位置、推车的速度、木杆的角度、木杆的角速度等

$$ x(s) = (x_1(s), x_2(s), \cdots,x_n(s))^T $$

此时价值函数 就可以用线性特征组合表示：

\[\hat{v}(s,w) = x(s)^Tw=\sum_{j=1}^nx_j(s)\cdot w_j \]

此时的损失函数为：

\[J(w) = E_\pi[(v_\pi(s) - x(s)^T w)^2] \]

因此更新规则为：

\[\Delta w = \alpha(v_\pi(s)-\hat{v}(s,w))\cdot x(s) \\ Update = StepSize\;*\;PredictionError\;*\;FeatureValue \]

二、预测过程中的价值函数逼近

因为我们函数逼近的就是 真实的状态价值，所以在实际的强化学习问题中是没有 \(v_\pi(s)\) 的，只有奖励。所以在函数逼近过程的监督数据为：

\[<S_1, G_1>, <S_2, G_2>, \cdots ,<S_t, G_T> \]

所以对于蒙特卡洛我们有：

\[\Delta w = \alpha({\color{red}G_t} - \hat{v}(s_t, w))\nabla_w\hat{v}(s_t, w) \\ = \alpha({\color{red}G_t} - \hat{v}(s_t, w)) \cdot x(s_t) \]

其中奖励 \(G_t\) 是无偏（unbiased）的：\(E[G_t] = v_\pi(s_t)\) 。值得一提的是，蒙特卡洛预测过程的函数逼近在线性或者是非线性都能收敛。

对于TD算法，我们使用 \(\hat{v}(s_t, w)\) 来代替 TD Target。所以我们在价值函数逼近（VFA）使用的训练数据如下所示：

\[<S_1, R_2+\gamma \hat{v}(s_2, w)>,<S_2, R_3+\gamma \hat{v}(s_3, w)>,\cdots,<S_{T-1}, R_T> \]

于是对于 TD(0) 在预测过程的函数逼近有：

\[\Delta w = \alpha({\color{red}R_{t+1} + \gamma \hat{v}(s_{t+1}, w)}-\hat{v}(s_t, w))\nabla_w\hat{v}(s_t, w) \\ = \alpha({\color{red}R_{t+1} + \gamma \hat{v}(s_{t+1}, w)}-\hat{v}(s_t, w))\cdot x(s) \]

因为TD中的 Target 中包含了预测的 \(\hat{v}(s,t)\) ，所以它对于真实的 \(v_\pi(s_t)\) 是有偏（biased）的，因为我们的监督数据是我们估计出来的，而不是真实的数据。也就是 \(E[R_{t+1} + \gamma \hat{v}(s_{t+1}, w)] \neq v_\pi(s_t)\) 。我们把这个过程叫做 semi-gradient，不是完全的梯度下降，而是忽略了权重向量 w 对 Target 的影响。

三、控制过程中的价值函数逼近

类比于MC 和 TD 在使用 Q 表格时的更新公式，对于策略控制过程我们可以得到如下公式。和上面预测过程一样，我们没有真实的 \(q_\pi(s,a)\) ，所以我们对其进行了替代：

• 对于 MC，Target 是 \(G_t\) ：

\[\Delta w = \alpha({\color{red}G_t} - \hat{q}(s_t, a_t, w))\nabla_w\hat{v}(s_t, a_t, w) \]

• 对于 Sarsa，TD Target 是 \(R_{t+1} + \gamma \hat{q}(s_{t+1}, a_{t+1}, w)\) :

\[\Delta w = \alpha ({\color{red}R_{t+1} + \gamma \hat{q}(s_{t+1}, a_{t+1}, w)} - \hat{q}{(s_t, s_t, w)})\cdot \nabla_w\hat{q}{(s_t, a_t, w)} \]

• 对于 Q-Learning，TD Target 是 \(R_{t+1} + \gamma\;max_a\; \hat{q}(s_{t+1}, a_t, w)\) :

\[\Delta w = \alpha ({\color{red}R_{t+1} + \gamma\;max_a\; \hat{q}(s_{t+1}, a_t, w)} - \hat{q}{(s_t, s_t, w)})\cdot \nabla_w\hat{q}{(s_t, a_t, w)} \]

四、关于收敛的问题

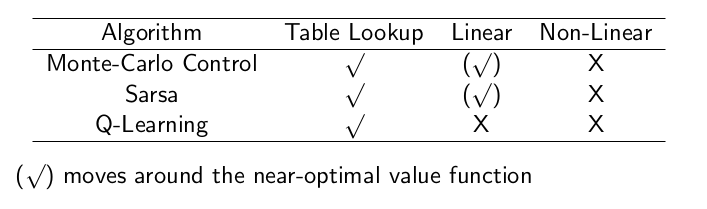
在上图中，对于使用 Q 表格的问题，不管是MC还是 Sarsa 和 Q-Learning 都能找到最优状态价值。如果是一个大规模的环境，我们采用线性特征拟合，其中MC 和 Sarsa 是可以找到一个近似最优解的。当使用非线性拟合（如神经网络），这三种算法都很难保证能找到一个最优解。

其实对于off-policy 的TD Learning强化学习过程收敛是很困难的，主要有以下原因：

• 使用函数估计：对于 Sarsa 和 Q-Learning 中价值函数的的近似，其监督数据 Target 是不等于真实值的，因为TD Target 中包含了需要优化的 参数 w，也叫作 半梯度TD，其中会存在误差。
• Bootstrapping：在更新式子中，上面红色字体过程中有 贝尔曼近似过程，也就是使用之前的估计来估计当前的函数，这个过程中也引入了不确定因素。（在这个过程中MC回比TD好一点，因为MC中代替 Target 的 \(G_t\) 是无偏的）。
• Off-policy 训练：对于 off-policy 策略控制过程中，我们使用 behavior policy 来采集数据，在优化的时候使用另外的 target policy 策略来优化，两种不同的策略会导致价值函数的估计变的很不准确。

上面三个因素就导致了强化学习训练的死亡三角，也是强化学习相对于监督学习训练更加困难的原因。

下一篇就来介绍本系列的第一个深度强化学习算法 Deep Q-Learning（DQN）

参考资料：

• B站周老师的 强化学习纲要第四节上