树状数组基础

树状数组简介

如果有哪一种数据结构可以支持区间/单点和的更新和查询，一个显而易见的答案就是万能的线段树。但是线段树虽然能支持很多的区间问题，但是代码量有些长。如果我们只是单纯地为了维护区间和其实并不用去专门构建一棵线段树。树状数组作为一种更加简单的，可以维护区间和的数据结构应运而生。

树状数组基本思想

对于数组\(A\)来说，如果我们要求​Sum(A_i , A_j)的结果，除了使用直接遍历或者是线段树，我们还可以为其定义一个数组\(C\)像下面这样：

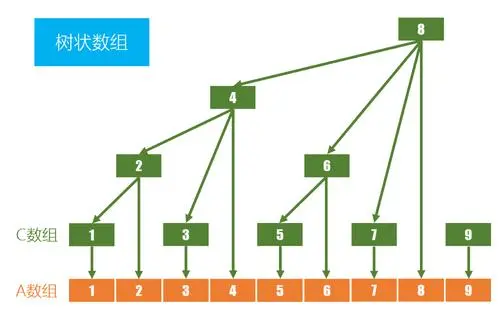
然后我们可以简单地罗列一个c数组到a数组到映射关系

A数组	C数组
A1	A1
A2	A1+A2
A3	A3
A4	A1+A2+A3+A4
A5	A5
A6	A5+A6
A7	A7
A8	A1+A2+A3+A4+A5+A6+A7+A8
A9	A9

我们可以把c数组看成一种特殊的前缀和。一般的前缀和的\(s~i~\)都是代表着\(A~i-A~0\) 的值，但是我们的c数组每一位代表着的值是像上面这个表写着的那样。

那么剩下的任务就是找规律了。最先可以看到的是对于\(A~i~\)​来说，如果i是奇数的话，那么有\(C~i~ = A~i~\)​。如果i是偶数的话，我们可以发现这样一条规律：设x为 i 的二进制形式中最低位1所代表的值，有\(C~i~ = Sum(A~x~ , A~1~)\)​​​ 。求出x值的函数我们一般称之为lowbit()函数，写法如下：

def lowbit(a):
	return a&(-a)

这样我们就可以完成C数组的维护。假设我们要在保持c数组维护着前缀和的性质的前提下更改A[1]的值（A[1]=A[1]+x），可以按照这样的顺序对C数组进行修改：

C[1]=C[1]+x lowbit(1)==1

C[2]=C[2]+x 1+lowbit(1)==2

C[4]=C[4]+x 2+lowbit(2)==4

C[8]=C[8]+x 4+lowbit(4)==8

写成代码就是这样：

def add(x,pos):
    while pos<=n:
        C[pos]+=x
	    pos=pos+lowbit(pos)

区间查询的思想和单点更新其实差不多（就是单点更新的反向操作），看看代码就能理解了：

def query(pos):
    ans=0
        while(pos>0):
	    ans+=tree[pos]
	    pos=pos-lowbit(pos)
    return ans

树状数组在逆序对上的应用

逆序对问题除了可以通过归并排序进行合并以外还可以用树状数组进行计算

逆序对问题就是求对于数组\(A\)来说，存在一组i,j使得i<j且\(A~i~>A~j~\) 我们称i，j为一组逆序对。逆序对问题通常是用归并排序的方式来分治计算，同时也可以用树状数组来计算

可以简单地把逆序对问题看成计算对于每一个数字，它前面有多少个比它大的数字，最后的答案就是对于每个数字的结果的和。首先，我们对输入数据进行离散化，因为输入数据大小可能会很大。然后，我们用离散化之后的数据下标构建一个全0树状数组。对于一个数，所有比它大的数字都可以通过计算下标数组上在他前面的数字的个数。此时就可以通过树状数组来加速计算的过程。

其实用线段树也可以进行计算，不过从代码量上来说还是树状数组更优一些。

树状数组可以被看作一种用来维护结合律支持的区间操作的一种代码量和细节都比较少的数据结构。如果要维护某些不支持结合律(比如说区间众数)之类的值的时候还是好好地打线段树吧