用 Python 通过马尔可夫随机场(MRF)与 Ising Model 进行二值图降噪
前言
这个降噪的模型来自 Christopher M. Bishop 的 Pattern Recognition And Machine Learning (就是神书 PRML……),问题是如何对一个添加了一定椒盐噪声(Salt-and-pepper Noise)(假设噪声比例不超过 10%)的二值图(Binary Image)去噪。
原图 -> 添加 10% 椒盐噪声的图:


放在 github 上的可运行完整代码:https://github.com/joyeecheung/simulated-annealing-denoising
建模
下文中的数学表示:
- yi:噪声图中的像素
- xi:原图中的像素,对应噪声图中的 yi
既然噪声图是从原图添加噪声而来,我们拥有了先验知识 1:
yi和xi有很强的联系。
一般图片里,每个像素和与它相邻的像素值应当较为接近,比如上图中的黑色笔画和白色负空间,除了边缘以外,黑色的像素周围都是黑色像素,白色像素的周围都是白色像素(连成一片))。这样我们就得到了先验知识 2:
xi和与它相邻的其他像素也存在较强的联系
如果我们狠一点,假设原图像素只与它的直接相邻像素有联系(即具备条件独立性质),我们就可以得到一个具备局部马尔可夫性质(Local Markov property)的图模型:

在这样一个图模型里,我们有两种团(clique):
- {xi, yi},即原图像素与噪声图像素对
- {xi, xj},其中 xj 表示与 xi 相邻的像素
这两种团合并起来,得到的 {xi, yi, xj} 显然是一个最大团(Maximal Clique),此时我们可以利用它来对这个马尔可夫随机场进行 factorization,即求得其联合概率分布关于最大团 xC = {xi, yi, xj} 的函数。
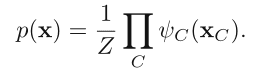
其中 Z 为 partition function,是 p(x) 的归一化常数(normalization constant),求法参见 PRML 8.3.2。因为与我们的实现不相关,这里不赘述。
ψC(xC) 即所谓的 potential function,为了方便我们通常只求它的对数形式 E(xC)(按照其物理意义称为 energy function)
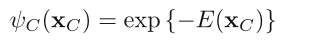
关于 factorization 的过程和推导可以参见 PRML 8.3.2,这里我们需要做的是定义一个 energy function。在降噪的过程中 energy 越低,联合概率 P(X=x) (降噪过的图像与原图一致的概率)就越大。
因为我们需要处理的是二值图,首先我们定义 xi ∈ {-1, +1},假设这里白色为1,黑色为-1。
对于原图像素与噪声图像素构成的团 {xi, yi},我们定义一项 −ηxiyi,其中 η 为一个非负的权重。当两者同号时,这项的值为−η,异号时为 η。这样,当噪声图像素与原图像素较为接近时,这一项能够降低 energy(因为为负)。
对于噪声图中相邻像素构成的团 {xi, xj},我们定义一项 −βxixj,其中 β 为一个非负的权重。这样,当处理过的图像里相邻的像素较为接近时,这一项能够降低 energy(因为为负)。
最后,我们再定义一项 hxi,使处理过的图像整体偏向某一个像素值。
对图像中的每一个像素,将这三项加起来,就得到我们的 energy function:
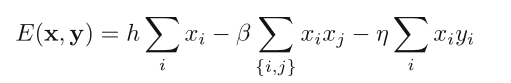
对应联合概率
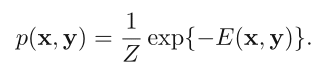
显然 energy 越低,降噪过的图像与原图一致的概率越高。(注意因为我们这里求的 E 已经对整个矩阵求和,即对应 potential function 的积,所以计算联合概率分布的时候不需要再求积)
使用 Python 实现这个 energy function 时,我们可以使用一个 closure 来实现一个 function factory,通过传递beta(β),eta(η)和 h 参数,生成对应的 energy function。此外为了方便,我们假设传入的x和y不是一维向量,而是对应图像的二维矩阵(注意是np.ndarray而不是nd.matrix,前者的*才是array multiplication即逐个元素相乘,后者的*是矩阵乘法)。
import numpy as np def E_generator(beta, eta, h): """Generate energy function E. Usage: E = E_generator(beta, eta, h) Formula: E = h * \sum{x_i} - beta * \sum{x_i x_j} - eta * \sum{x_i y_i} """ def E(x, y): """Calculate energy for matrices x, y. Note: the computation is not localized, so this is quite expensive. """ # sum of products of neighboring paris {xi, yi} xxm = np.zeros_like(x) xxm[:-1, :] = x[1:, :] # down xxm[1:, :] += x[:-1, :] # up xxm[:, :-1] += x[:, 1:] # right xxm[:, 1:] += x[:, :-1] # left xx = np.sum(xxm * x) xy = np.sum(x * y) xsum = np.sum(x) return h * xsum - beta * xx - eta * xy return E
注意到如果用 xi0 ~ xi3 表示 xi 的四个邻居,则 xi * xi0 + xi * xi1 + xi * xi2 + xi * xi3 = + xi * (xi1 + ... + xi3),即乘法结合律,因此我们可以先将邻居相加,再与 x相乘。
因为边界元素不一定有四个邻居,−βxixj这项存在边界问题,我们需要特别处理,利用 numpy 的 fancy index,写起来并不困难,即上面代码中的:
# sum of products of neighboring paris {xi, yi} xxm = np.empty_like(x) xxm[:-1, :] = x[1:, :] # down xxm[1:, :] += x[:-1, :] # up xxm[:, :-1] += x[:, 1:] # right xxm[:, 1:] += x[:, :-1] # left xx = np.sum(xxm * x)
即将每个元素的邻居都都加起来存储在x中,然后用np.sum(xxm * x)求得积。
注意这里生成的E每次都要对矩阵中的所有元素进行运算,所以即使有 numpy 加持,开销依然较大。后面我们会按照需求进行优化。
得到了 energy function 的表示,接下来我们需要做的就是想办法让处理过后的图像具备尽可能低的 energy,从而获得更高的概率 P(X=x)。
注意如果我们固定 y 作为先验知识(假设噪声图不变),我们所求的概率就变成了 p(x|y),这种模型叫做 Ising Model,在统计物理中有广泛的应用。这样我们的问题就成了以 y 为基准,想办法不断变动 x,然后找出最接近原图的 x。
Iterated Conditional Modes
一种最简单的办法是我们先将 x 初始化为 y,然后遍历每一个元素,对每个元素分别尝试 1 和 -1 两种状态,选择能够得到更高的 energy 的那个,实际上相当于一种贪心的策略。这种方法称为 Iterated Conditional Modes(ICM),由 Julian Besag 在 1986 年的论文 On the Statistical Analysis of Dirty Pictures 中提出(这篇论文在 80 年代英国数学家所著论文里引用数排名第一……)。
因为 ICM 的每一步实际上固定住了其他元素,只变动当前遍历到的那个元素,所以我们可以将 E的计算 localize,只对受影响的那一小片区域重新计算。我们可以让 function factory E_generator 返回两个版本的 E,一个是全局的,用于第一次计算 E,一个是局部的,用于计算某个元素两种状态下的 E。
def E_generator(beta, eta, h): def E(x, y): ... # as shown before def is_valid(i, j, shape): """Check if coordinate i, j is valid in shape.""" return i >= 0 and j >= 0 and i < shape[0] and j < shape[1] def localized_E(E1, i, j, x, y): """Localized version of Energy function E. Usage: old_x_ij, new_x_ij, E1, E2 = localized_E(Ecur, i, j, x, y) """ oldval = x[i, j] newval = oldval * -1 # flip # local computations E2 = E1 - (h * oldval) + (h * newval) E2 = E2 + (eta * y[i, j] * oldval) - (eta * y[i, j] * newval) adjacent = [(0, 1), (0, -1), (1, 0), (-1, 0)] neighbors = [x[i + di, j + dj] for di, dj in adjacent if is_valid(i + di, j + dj, x.shape)] E2 = E2 + beta * sum(a * oldval for a in neighbors) E2 = E2 - beta * sum(a * newval for a in neighbors) return oldval, newval, E1, E2 return E, localized_E
localized_E 将 x[i, j] 更改为另一状态,减去原来状态在 E 里对应的那几项,计算新状态对应的项,再加上去。adjacent和neighbors均是为了过滤掉非法的边界元素而设。
ICM 的实现如下,为了方便画图查看 energy 变化情况,在每遍历完一行的时候,我们可以记录当前的时间和 energy:
def ICM(y, E, localized_E): """Greedy version of simulated_annealing().""" x = np.array(y) Ebest = Ecur = E(x, y) # initial energy initial_time = time.time() energy_record = [[0.0, ], [Ebest, ]] accept, reject = 0, 0 for idx in np.ndindex(y.shape): # for each pixel in the matrix old, new, E1, E2 = localized_E(Ecur, idx[0], idx[1], x, y) if (E2 < Ebest): Ecur, x[idx] = E2, new Ebest = E2 # update Ebest else: Ecur, x[idx] = E1, old # record time and Ebest of this iteration end_time = time.time() energy_record[0].append(end_time - initial_time) energy_record[1].append(Ebest) return x, energy_record
为了方便将二值图像素在{0, 255}(黑与白的颜色值)与 {-1, +1}之间转换,写一个小函数:
def sign(data, translate): """Map a dictionary for the element of data. Example: To convert every element in data with value 0 to -1, 255 to 1, use `signed = sign(data, {0: -1, 255: 1})` """ temp = np.array(data) return np.vectorize(lambda x: translate[x])(temp)
接下来在在 ipython 里看看结果。设 beta, eta, h = 1e-3, 2.1e-3, 0.0:
In [21]: beta, eta, h = 1e-3, 2.1e-3, 0.0 In [22]: im = Image.open('flipped.png') In [23]: data = sign(im.getdata(), {0: -1, 255: 1}) # convert to {-1, 1} In [24]: y = data.reshape(im.size[::-1]) # to matrix In [25]: E, localized_E = E_generator(beta, eta, h) In [26]: result, energy_record = ICM(y, E, localized_E) In [27]: result = sign(result, {-1: 0, 1: 255}) In [28]: output_image = Image.fromarray(result).convert('1', dither=Image.NONE)
查看去噪结果
output_image.show()

对比一下原图与噪声图,可以看到去掉了相当一部分噪点,但比较密集的噪点形成团块留了下来(因为我们只算四连通的相邻像素,所以很小范围内的噪点聚集都会形成团块):


查看 time-energy 关系图:
In [30]: plt.plot(*energy_record) Out[30]: [<matplotlib.lines.Line2D at 0xa63ecd0>] In [31]: plt.xlabel('Time(s)') Out[31]: <matplotlib.text.Text at 0xa5efb70> In [32]: plt.ylabel('Energy') Out[32]: <matplotlib.text.Text at 0xa5f3b70> In [33]: plt.show()

看看降噪之后与原图的相似度:
In [60]: original = Image.open('in.png') In [61]: x = np.reshape(original.getdata(), original.size[::-1]) In [62]: 1 - np.count_nonzero(x - result) / float(x.size) Out[62]: 0.9621064814814815
可以看到大约 96% 的像素与原图一致。不过光从视觉上看,降噪过后的图依然有不少明显的噪点,这是因为 ICM 采取的类似贪心的策略使得它容易陷入局部最优(local optimum)。如果想要得到一个更好的降噪结果,我们显然要采取一种能够得到全局最优(global optimum)的策略。
模拟退火
其实这个问题可以看成一个搜索问题:在所有 x 的两种状态组成的状态空间里(假设有 n 个像素,那么状态空间大小为 2n),找到能使 energy 最低的状态。由于状态空间大小呈指数级增长,仅仅是对于一个有 240 × 180 = 43,200 个像素的图片来说,这个状态空间就已经不可能使用暴力搜索解决了(实际上是 NP-Hard 的),所以我们需要考虑其他的搜索策略。这里我们可以尝试使用模拟退火(Simulated annealing),在有限的时间内找到尽可能好的解。本方法由 Stuart Geman 与 Donald Geman (兄弟哟) 在 1984 年的论文 Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images 中提出,并且文中对模拟退火可收敛至全局最优进行了详细的证明(这篇论文和之前 Julian Besag 的那篇都是 ISI Highly Cited Paper,引用数相当魔性……)。
模拟退火需要一个控制温度的 schedule,具体怎样可以自己调,只需要在迭代次数 k 接近最大迭代次数 kmax 时逼近 0 即可,这里设定为:
def temperature(k, kmax): """Schedule the temperature for simulated annealing.""" return 1.0 / 500 * (1.0 / k - 1.0 / kmax)
模拟退火的核心在于当局部变化导致状况恶化(这里为能量变大)时,依据当前温度 t,设该变化对全局最优有利的概率为 e△E/t,按照这个概率来确定是否保留这个变化,即所谓的 transition probabilities,如下:
def prob(E1, E2, t): """Probability transition function for simulated annealing.""" return 1 if E1 > E2 else np.exp((E1 - E2) / t)
下面是模拟退火方法的实现,因为模拟退火会进行多次迭代,不断逼近最优,我们这里可以将中途结果输出来看看(这里顺手往参数列表塞了个存中间结果的文件夹……)
def simulated_annealing(y, kmax, E, localized_E, temp_dir): """Simulated annealing process for image denoising. Parameters ---------- y: array_like The noisy binary image matrix ranging in {-1, 1}. kmax: int The maximun number of iterations. E: function Energy function. localized_E: function Localized version of E. temp_dir: path Directory to save temporary results. Returns ---------- x: array_like The denoised binary image matrix ranging in {-1, 1}. energy_record: [time, Ebest] records for plotting. """ x = np.array(y) Ebest = Ecur = E(x, y) # initial energy initial_time = time.time() energy_record = [[0.0, ], [Ebest, ]] for k in range(1, kmax + 1): # iterate kmax times start_time = time.time() t = temperature(k, kmax + 1) print "k = %d, Temperature = %.4e" % (k, t) accept, reject = 0, 0 # record the acceptance of alteration for idx in np.ndindex(y.shape): # for each pixel in the matrix old, new, E1, E2 = localized_E(Ecur, idx[0], idx[1], x, y) p, q = prob(E1, E2, t), random() if p > q: accept += 1 Ecur, x[idx] = E2, new if (E2 < Ebest): Ebest = E2 # update Ebest else: reject += 1 Ecur, x[idx] = E1, old # record time and Ebest of this iteration end_time = time.time() energy_record[0].append(end_time - initial_time) energy_record[1].append(Ebest) print "k = %d, accept = %d, reject = %d" % (k, accept, reject) print "k = %d, %.1f seconds" % (k, end_time - start_time) # save temporary results temp = sign(x, {-1: 0, 1: 255}) temp_path = os.path.join(temp_dir, 'temp-%d.png' % (k)) Image.fromarray(temp).convert('1', dither=Image.NONE).save(temp_path) print "[Saved]", temp_path return x, energy_record
再看看结果,设beta, eta, h, kmax = 1e-3, 2.1e-3, 0.0, 15
从上到下,从左到右,k = 1, 5, 10, 15




time-energy 关系图

用对 ICM 一样的方法进行统计,结果是 99.16% 的像素与原图一致。
最终结果:原图->噪声图->ICM->模拟退火




后话
无论是 ICM 还是模拟退火,都是通过最小化能量来找到原图的近似。后来 Greig, Porteous 和 Seheult 提出了使用 graph cuts 的模型,将能量值的最小化转化为最大化解的后验估计(a posteriori estimate),进而转为计算机科学里常见的 max-flow/min-cut 的问题,求解后能够得到更好的效果(参考 D.M. Greig, B.T. Porteous and A.H. Seheult (1989), Exact maximum a posteriori estimation for binary images, Journal of the Royal Statistical Society Series B, 51, 271–279.)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号