算法
1、数据结构
堆
class BinaryHeap {
private int[] elements;
private int size;
private static final int DEFAULT_CAPACITY = 10;
public BinaryHeap(int[] elements, int k) {
if (elements == null || elements.length == 0) {
this.elements = new int[k];
} else {
size = elements.length;
int capacity = Math.max(DEFAULT_CAPACITY, size);
this.elements = new int[capacity];
for (int i = 0; i < elements.length; i++) {
this.elements[i] = elements[i];
}
}
heapify();
}
public BinaryHeap(int k) {
this(null, k);
}
private void heapify() {
for (int i = (size >> 1) - 1; i >= 0; i--) {
siftDown(i);
}
}
// 向堆添加一个元素
public void offer(int element) {
elements[size++] = element;
siftUp(size - 1);
}
public int peek() {
return elements[0];
}
//
public int remove(int element) {
int lastIndex = --size;
int root = elements[lastIndex];
elements[0] = elements[lastIndex];
elements[lastIndex] = 0;
siftDown(0);
return root;
}
private void siftUp(int index) {
// 先将要上滤的值保存下来
int element = elements[index];
while (index > 0) {
int parentIndex = (index - 1) >> 1;
int parent = elements[parentIndex];
// 我们要弄小顶堆
if (parent <= element) {
break;
}
elements[index] = parent;
index = parentIndex;
}
elements[index] = element;
}
private void siftDown(int index) { // 删除完堆顶进行处理index开始就是0
int element = elements[index]; // 先将要下滤的元素拿出来,放在一边!
int half = size >> 1; // 第一个叶子节点的索引 == 非叶子节点的数量
// index < 第一个叶子节点的索引
// 必须保证index位置是非叶子节点
while (index < half) {
// index的节点有2种情况
// 1.只有左子节点,肯定不会是右子节点。(不可能出现有右无左!)
// 2.同时有左右子节点
// 默认为左子节点跟它进行比较
int childIndex = (index << 1) + 1; // (2i + 1)是左子节点的索引!
int child = elements[childIndex];
// 右子节点
int rightIndex = childIndex + 1; // (左子节点索引位置加1就是右子节点索引的位置!)
// 索引的范围是 (0---size-1);
// 选出左右子节点最大的那个(右边比左边大的话,就用右边喽!)
if (rightIndex <= size - 1 && elements[rightIndex] < child) { //右子节点的索引在有效范围内
child = elements[childIndex = rightIndex];
}
if (element <= child) {
break;
}
// 将子节点存放到index位置
elements[index] = child;//将子节点中大的元素挪到自己的位置上!
// 重新设置index
index = childIndex;
}
elements[index] = element;
}
}
单调队列
/* 单调队列的实现,可以高效维护最大值和最小值 */
class MonotonicQueue<E extends Comparable<E>> {
// 常规队列,存储所有元素
LinkedList<E> q = new LinkedList<>();
// 元素降序排列的单调队列,头部是最大值
LinkedList<E> maxq = new LinkedList<>();
// 元素升序排列的单调队列,头部是最小值
LinkedList<E> minq = new LinkedList<>();
public void push(E elem) {
// 维护常规队列,直接在队尾插入元素
q.addLast(elem);
// 维护 maxq,将小于 elem 的元素全部删除
while (!maxq.isEmpty() && maxq.getLast().compareTo(elem) < 0) {
maxq.pollLast();
}
maxq.addLast(elem);
// 维护 minq,将大于 elem 的元素全部删除
while (!minq.isEmpty() && minq.getLast().compareTo(elem) > 0) {
minq.pollLast();
}
minq.addLast(elem);
}
public E max() {
// maxq 的头部是最大元素
return maxq.getFirst();
}
public E min() {
// minq 的头部是最大元素
return minq.getFirst();
}
public E poll(E val) {
E deleteVal = q.removeFirst();
if (val == maxq.peek()) {
maxq.removeFirst();
}
if (val == minq.peek()) {
minq.removeFirst();
}
return deleteVal;
}
public E pop() {
// 从标准队列头部弹出需要删除的元素
E deleteVal = q.pollFirst();
assert deleteVal != null;
// 由于 push 的时候会删除元素,deleteVal 可能已经被删掉了
if (deleteVal.equals(maxq.getFirst())) {
maxq.pollFirst();
}
if (deleteVal.equals(minq.getFirst())) {
minq.pollFirst();
}
return deleteVal;
}
public int size() {
// 标准队列的大小即是当前队列的大小
return q.size();
}
public boolean isEmpty() {
return q.isEmpty();
}
}
LRU
class LRUCache {
// 1.构建哈希
private final Map<Integer, DoubleLinkedNode> cache = new HashMap<>();
// 几个全局变量:链表大小,容量
private int size;
private final int capacity;
// 双向链表中,构造两个节点,伪头结点和伪尾节点,方便插入删除其他节点
private final DoubleLinkedNode dummyHead;
private final DoubleLinkedNode dummyTail;
// 2.构建双向链表模型
static class DoubleLinkedNode {
// 键值对
int key;
int value;
// 前后节点
DoubleLinkedNode prev;
DoubleLinkedNode next;
// 无参和有参构造
public DoubleLinkedNode() {
}
public DoubleLinkedNode(int k, int v) {
this.key = k;
this.value = v;
}
}
// 构造函数
public LRUCache(int capacity) {
this.size = 0;
this.capacity = capacity;
// 两个虚拟节点就不指定kv了吧
dummyHead = new DoubleLinkedNode();
dummyTail = new DoubleLinkedNode();
dummyHead.next = dummyTail;
dummyTail.prev = dummyHead;
}
// get方法,访问元素,移动到链表头部。
public int get(int key) {
// 1.查询哈希
DoubleLinkedNode node = cache.get(key);
// 为空返回-1
if (node == null) {
return -1;
}
// 2.哈希查询到,将该节点移动到头部
moveToHead(node);
return node.value;
}
// put方法
public void put(int key, int value) {
// 1.哈希查询,若不存在节点,则添加。
DoubleLinkedNode node = cache.get(key);
if (node == null) {
// 创建节点,添加链表,添加哈希,增加size。
DoubleLinkedNode newNode = new DoubleLinkedNode(key, value);
// 新节点加入哈希,保存key和Node的映射关系。
cache.put(key, newNode);
// 新节点加入头部。
addToHead(newNode);
// LRU中存储的元素加1。
++size;
// size超出capacity,在链表和哈希中删除尾节点。
// 将尾节点从双向链表中移除,并且将其key和Node的映射关系从hash表中移除。
if (size > capacity) {
DoubleLinkedNode tail = removeTail();
cache.remove(tail.key);
--size;
}
} else {
// 若哈希中存在该节点,覆盖更新链表中的值,并移动该节点到头部作为最近使用。
node.value = value;
moveToHead(node);
}
}
// 辅助方法区:
// 1.将节点移动到头部
private void moveToHead(DoubleLinkedNode node) {
// 删除节点
removeNode(node);
// 头部添加该节点
addToHead(node);
}
// 2.删除节点
private void removeNode(DoubleLinkedNode node) {
node.prev.next = node.next;
node.next.prev = node.prev;
}
// 3.头部添加节点
private void addToHead(DoubleLinkedNode node) {
node.prev = dummyHead;
node.next = dummyHead.next;
dummyHead.next.prev = node;
dummyHead.next = node;
}
// 4.删除尾节点,并返回被删除的节点
private DoubleLinkedNode removeTail() {
DoubleLinkedNode tail = dummyTail.prev;
removeNode(tail);
return tail;
}
}
LFU
一定先从最简单的开始,根据 LFU 算法的逻辑,我们先列举出算法执行过程中的几个显而易见的事实:
1、调用 get(key) 方法时,要返回该 key 对应的 val。
2、只要用 get 或者 put 方法访问一次某个 key,该 key 的 freq 就要加一。
3、如果在容量满了的时候进行插入,则需要将 freq 最小的 key 删除,如果最小的 freq 对应多个 key,则删除其中最旧的那一个。
好的,我们希望能够在 O(1) 的时间内解决这些需求,可以使用基本数据结构来逐个击破:
1、使用一个 HashMap 存储 key 到 val 的映射,就可以快速计算 get(key)。
HashMap<Integer, Integer> keyToVal;
2、使用一个 HashMap 存储 key 到 freq 的映射,就可以快速操作 key 对应的 freq。
HashMap<Integer, Integer> keyToFreq;
3、这个需求应该是 LFU 算法的核心,所以我们分开说:
3.1、首先,肯定是需要 freq 到 key 的映射,用来找到 freq 最小的 key;
3.2、将 freq 最小的 key 删除,那你就得快速得到当前所有 key 最小的 freq 是多少;
想要时间复杂度 O(1) 的话,肯定不能遍历一遍去找,那就用一个变量 minFreq 来记录当前最小的 freq 吧;
3.3、可能有多个 key 拥有相同的 freq,所以 freq 对 key 是一对多的关系,即一个 freq 对应一个 key 的列表;
3.4、希望 freq 对应的 key 的列表是存在时序的,便于快速查找并删除最旧的 key;
3.5、希望能够快速删除 key 列表中的任何一个 key,因为如果频次为 freq 的某个 key 被访问,那么它的频次就会变成 freq+1,就应该从 freq 对应的 key
列表中删除,加到 freq+1 对应的 key 的列表中。
HashMap<Integer, LinkedHashSet<Integer>> freqToKeys;
int minFreq = 0;
介绍一下这个 LinkedHashSet,它满足我们 3.3,3.4,3.5 这几个要求。你会发现普通的链表 LinkedList 能够满足 3.3,3.4 这两个要求,但是由于普通链表不
能快速访问链表中的某一个节点,所以无法满足 3.5 的要求。
LinkedHashSet 顾名思义,是链表和哈希集合的结合体。
链表不能快速访问链表节点,但是插入元素具有时序;哈希集合中的元素无序,但是可以对元素进行快速的访问和删除。
那么,它俩结合起来就兼具了哈希集合和链表的特性,既可以在 O(1) 时间内访问或删除其中的元素,又可以保持插入的时序,高效实现 3.5 这个需求。
综上,我们可以写出 LFU 算法的基本数据结构:
class LFUCache {
// key 到 val 的映射,我们后文称为 KV 表
HashMap<Integer, Integer> keyToVal;
// key 到 freq 的映射,我们后文称为 KF 表
HashMap<Integer, Integer> keyToFreq;
// freq 到 key 列表的映射,我们后文称为 FK 表
HashMap<Integer, LinkedHashSet<Integer>> freqToKeys;
// 记录最小的频次
int minFreq;
// 记录 LFU 缓存的最大容量
int cap;
public LFUCache(int capacity) {
keyToVal = new HashMap<>();
keyToFreq = new HashMap<>();
freqToKeys = new HashMap<>();
this.cap = capacity;
this.minFreq = 0;
}
public int get(int key) {}
public void put(int key, int val) {}
}
class LFUCache {
// key 到 val 的映射,我们后文称为 KV 表
HashMap<Integer, Integer> keyToVal;
// key 到 freq 的映射,我们后文称为 KF 表
HashMap<Integer, Integer> keyToFreq;
// freq 到 key 列表的映射,我们后文称为 FK 表
HashMap<Integer, LinkedHashSet<Integer>> freqToKeys;
// 记录最小的频次
int minFreq;
// 记录 LFU 缓存的最大容量
int capacity;
public LFUCache(int capacity) {
keyToVal = new HashMap<>();
keyToFreq = new HashMap<>();
freqToKeys = new HashMap<>();
this.capacity = capacity;
this.minFreq = 0;
}
public int get(int key) {
// 查询kv映射表,
if (!keyToVal.containsKey(key)) {
return -1;
}
// 增加 key 对应的 freq
increaseFreq(key);
return keyToVal.get(key);
}
public void put(int key, int val) {
if (this.capacity <= 0) return;
/* 若 key 已存在,修改对应的 val 即可 */
if (keyToVal.containsKey(key)) {
keyToVal.put(key, val);
// key 对应的 freq 加一
increaseFreq(key);
return;
}
/* key 不存在,需要插入 */
/* 容量已满的话需要淘汰一个 freq 最小的 key */
if (this.capacity <= keyToVal.size()) {
removeMinFreqKey();
}
/* 插入 key 和 val,对应的 freq 为 1 */
// 插入 KV 表
keyToVal.put(key, val);
// 插入 KF 表
keyToFreq.put(key, 1);
// 插入 FK 表
freqToKeys.putIfAbsent(1, new LinkedHashSet<>());
freqToKeys.get(1).add(key);
// 插入新 key 后最小的 freq 肯定是 1
this.minFreq = 1;
}
private void increaseFreq(int key) {
int freq = keyToFreq.get(key);
/* 更新 KF 表 */
keyToFreq.put(key, freq + 1);
/* 更新 FK 表 */
// 将 key 从 freq 对应的列表中删除
freqToKeys.get(freq).remove(key);
// 将 key 加入 freq + 1 对应的列表中
freqToKeys.putIfAbsent(freq + 1, new LinkedHashSet<>());
freqToKeys.get(freq + 1).add(key);
// 如果 freq 对应的列表空了,移除这个 freq
if (freqToKeys.get(freq).isEmpty()) {
freqToKeys.remove(freq);
// 如果这个 freq 恰好是 minFreq,更新 minFreq。
// 就是说当前最小频率minFreq的key集合元素都移动到了minFreq + 1对应的LinkedHashSet集合中,此时就需要更新minFreq。
if (freq == this.minFreq) {
this.minFreq++;
}
}
}
// 删除频率最小的key
private void removeMinFreqKey() {
// freq 最小的 key 列表
LinkedHashSet<Integer> keyList = freqToKeys.get(this.minFreq);
// 其中最先被插入的那个 key 就是该被淘汰的 key
int deletedKey = keyList.iterator().next();
/* 更新 FK 表 */
keyList.remove(deletedKey);
if (keyList.isEmpty()) {
freqToKeys.remove(this.minFreq);
// 问:这里需要更新 minFreq 的值吗? 其实是不需要的。
}
/* 更新 KV 表 */
keyToVal.remove(deletedKey);
/* 更新 KF 表 */
keyToFreq.remove(deletedKey);
}
}
Trie
295. 数据流的中位数
中位数是有序列表中间的数。如果列表长度是偶数,中位数则是中间两个数的平均值。
例如,
[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
- void addNum(int num) - 从数据流中添加一个整数到数据结构中;
- double findMedian() - 返回目前所有元素的中位数。
class MedianFinder {
PriorityQueue<Integer> minHeap;
PriorityQueue<Integer> maxHeap;
public MedianFinder() {
// 优先级队列默认是小顶堆,存储较大的元素。
minHeap = new PriorityQueue<>();
// 添加比较器变为大顶堆,存储较小的元素。
maxHeap = new PriorityQueue<>((x, y) -> (y - x));
}
// 时间复杂度是O(logN)
// 如果最终元素是奇数个,我们让小顶堆元素多一个。
// 在添加到大顶堆之前为什么要先添加到小顶堆里面,然后再把小顶堆的堆顶元素添加到大顶堆中。
// 因为如果直接向大顶堆添加元素,这个元素的值要是比小顶堆中的所有元素都小还好说,它本应该属于大顶堆中。
// 不过要是添加的元素值比小顶堆中的一部分值大,直接添加进大顶堆就不对了,因为它肯定比大顶堆中的所有元素大
// 放在堆顶,但是它还大于小顶堆中的一部分元素。导致求出了错误的中位数。
// 先添加到小顶堆中处理好大小关系,确保将小顶堆中的最小元素,添加到大顶堆中。
public void addNum(int num) {
if (minHeap.size() > maxHeap.size()) {
minHeap.add(num);
maxHeap.add(minHeap.poll());
} else {
maxHeap.add(num);
minHeap.add(maxHeap.poll());
}
}
// O(1)时间复杂度
public double findMedian() {
// 如果两个堆的元素一样,分别取两个堆顶的元素,求和除以2.
if (minHeap.size() == maxHeap.size()) {
return (maxHeap.peek() + minHeap.peek()) / 2.0;
} else {
// 小顶堆元素更多,中位数就是这个多的元素,小顶堆存放的是较大的数。
return minHeap.peek();
}
}
}
380. O(1) 时间插入、删除和获取随机元素
实现RandomizedSet 类:
- RandomizedSet() 初始化 RandomizedSet 对象;
- bool insert(int val) 当元素 val 不存在时,向集合中插入该项,并返回 true ;否则,返回 false ;
- bool remove(int val) 当元素 val 存在时,从集合中移除该项,并返回 true ;否则,返回 false ;
- int getRandom() 随机返回现有集合中的一项(测试用例保证调用此方法时集合中至少存在一个元素)。每个元素应该有 相同的概率 被返回。
你必须实现类的所有函数,并满足每个函数的 平均 时间复杂度为 O(1) 。
本题的难点在于两点:
1、插入,删除,获取随机元素这三个操作的时间复杂度必须都是 O(1);
2、getRandom 方法返回的元素必须等概率返回随机元素,也就是说,如果集合里面有 n 个元素,每个元素被返回的概率必须是 1/n。
我们先来分析一下:对于插入,删除,查找这几个操作,哪种数据结构的时间复杂度是 O(1)?
HashSet 肯定算一个对吧。哈希集合的底层原理就是一个大数组,我们把元素通过哈希函数映射到一个索引上。
如果用拉链法解决哈希冲突,那么这个索引可能连着一个链表或者红黑树。
那么请问对于这样一个标准的 HashSet,你能否在 O(1) 的时间内实现 getRandom 函数?
其实是不能的,因为根据刚才说到的底层实现,元素是被哈希函数「分散」到整个数组里面的,更别说还有拉链法等等解决哈希冲突的机制,所以做不到 O(1) 时
间「等概率」随机获取元素。
除了 HashSet,还有一些类似的数据结构,比如哈希链表 LinkedHashSet,我们后文 手把手实现LRU算法 和 手把手实现LFU算法 讲过这类数据结构的实现原
理,本质上就是哈希表配合双链表,元素存储在双链表中。
但是,LinkedHashSet 只是给 HashSet 增加了有序性,依然无法按要求实现我们的 getRandom 函数,因为底层用链表结构存储元素的话,是无法在 O(1) 的时
间内访问某一个元素的。
根据上面的分析,对于 getRandom 方法,如果想「等概率」且「在 O(1) 的时间」取出元素,一定要满足:底层用数组实现,且数组必须是紧凑的。
这样我们就可以直接生成随机数作为索引,从数组中取出该随机索引对应的元素,作为随机元素。
但如果用数组存储元素的话,插入,删除的时间复杂度怎么可能是 O(1) 呢?
可以做到!对数组尾部进行插入和删除操作不会涉及数据搬移,时间复杂度是 O(1)。
所以,如果我们想在 O(1) 的时间删除数组中的某一个元素 val,可以先把这个元素交换到数组的尾部,然后再 pop 掉。
交换两个元素必须通过索引进行交换对吧,那么我们需要一个哈希表 valToIndex 来记录每个元素值对应的索引。
有了思路铺垫,我们直接看代码:
class RandomizedSet {
// 存放元素
List<Integer> nums;
// 记录每个元素在nums中的索引
Map<Integer, Integer> indexes;
Random random;
public RandomizedSet() {
nums = new ArrayList<>();
indexes = new HashMap<>();
random = new Random();
}
public boolean insert(int val) {
// 存在,不插入
if (indexes.containsKey(val)) {
return false;
}
// 获取val的索引,因为要插入到最后。
int valIndex = nums.size();
// val为key valIndex为value 存入map中
indexes.put(val, valIndex);
// 记录元素
nums.add(val);
return true;
}
public boolean remove(int val) {
// 不存在,不删除
if (!indexes.containsKey(val)) {
return false;
}
// 拿到当前值的索引
int valIndex = indexes.get(val);
// 拿到当前末尾的数
int lastNum = nums.get(nums.size() - 1);
// 把要删除数val索引valIndex的值,替换为数组的最后一个数lastNum
nums.set(valIndex, lastNum);
// 索引map中,把末位数字的索引值,更新为要删除数字val的索引值
indexes.put(lastNum, valIndex);
// 数组移除末尾元素
nums.remove(nums.size() - 1);
// 索引集合移除要删除的key
indexes.remove(val);
return true;
}
public int getRandom() {
// 从[0, nums.size())中随机选择一个索引。从nums数组中获取元素。
int index = random.nextInt(nums.size());
return nums.get(index);
}
}
710. 黑名单中的随机数
给定一个整数 n 和一个 无重复 黑名单整数数组 blacklist 。设计一种算法,从 [0, n - 1] 范围内的任意整数中选取一个 未加入 黑名单 blacklist 的整
数。任何在上述范围内且不在黑名单 blacklist 中的整数都应该有 同等的可能性 被返回。
优化你的算法,使它最小化调用语言 内置 随机函数的次数。
实现 Solution 类:
- Solution(int n, int[] blacklist) 初始化整数 n 和被加入黑名单 blacklist 的整数;
- int pick() 返回一个范围为 [0, n - 1] 且不在黑名单 blacklist 中的随机整数。
解题思路:
class Solution {
private final HashMap<Integer, Integer> mapping;
private final Random random;
private final int size;
public Solution(int n, int[] blacklist) {
mapping = new HashMap();
random = new Random();
size = n - blacklist.length;
// 先把黑名单中的数放在哈希表中
for (int black : blacklist) {
mapping.put(black, 666);
}
int last = n - 1;
for (int black : blacklist) {
// 如果黑名单中的数已经在后面部分了不用做处理,因为随机时取不到这里。
if (black > size - 1) {
continue;
}
// 如果last指向的位置就是黑名单中的数,此时不能做索引映射,应该找到第一个不是黑名单中的数。
while (mapping.containsKey(last)) {
last--;
}
// 用map来存储前n - blacklist.length个数中属于黑名单中的数和后面剩下的数中非黑名单中的数的映射关系。
mapping.put(black, last);
last--;
}
}
public int pick() {
int index = random.nextInt(size);
return mapping.containsKey(index) ? mapping.get(index) : index;
}
}
2、算法
排序算法

1. 冒泡排序
冒泡排序也叫做起泡排序。
执行流程
① 从头开始比较每一对相邻元素,如果第1个比第2个大,就交换它们的位置执行完一轮后,最未尾那个元素就是最大的元素;
② 忽略①中曾经找到的最大元素,重复执行步骤①,直到全部元素有序。
第一次写的代码如下:
public class Test {
public static void main(String[] args) {
int[] nums = new int[]{5, 989, 52, 96, 32, 748412, 125415};
for (int i = 0; i < nums.length; i++) {
for (int j = 1; j < nums.length; j++) {
if (nums[j] < nums[j - 1]) {
int temp = nums[j - 1];
nums[j - 1] = nums[j];
nums[j] = temp;
}
}
}
for (int num : nums) {
System.out.println(num);
}
}
}
这种写法根本就没有利用到每次找到的最大的元素,每次都要比较到数组最后一个元素,那么就多了一些不必要的比较。改进如下:
public static int[] BubbleSort(int[] nums) {
// 每排好序一次就缩减end
for (int end = nums.length - 1; end > 0; end--) {
for (int i = 1; i <= end; i++) {
if (nums[i] < nums[i - 1]) {
int temp = nums[i - 1];
nums[i - 1] = nums[i];
nums[i] = temp;
}
}
}
return nums
}
再针对序列完全有序的情况,做出如下的优化:
public static int[] BubbleSort(int[] nums) {
for (int end = nums.length - 1; end > 0; end--) {
boolean sorted = true;
for (int i = 1; i <= end; i++) {
if (nums[i] < nums[i - 1]) {
int temp = nums[i - 1];
nums[i - 1] = nums[i];
nums[i] = temp;
sorted = false;
}
}
if (sorted) {
break;
}
}
return nums;
}
最坏、平均时间复杂度:O(n^2);
最好时间复杂度: O ( n ) ;
空间复杂度: O ( 1 );
冒泡排序属于 In-place;
冒泡排序属于稳定的排序算法。
2. 选择排序
执行流程:
① 从序列中找出最大的那个元素,然后与最未尾的元素交换位置执行完一轮后,最未尾的那个元素就是最大的元素;
② 忽略①中曾经找到的最大元素,重复执行步骤①。
public static int[] SelectionSort(int[] nums) {
for (int end = nums.length - 1; end > 0; end--) {
int maxIndex = 0;
for (int i = 1; i <= end; i++) {
if (nums[i] > nums[maxIndex]) {
max = i;
}
}
int temp = nums[maxIndex];
nums[maxIndex] = nums[end];
nums[end] = temp;
}
return nums;
}
选择排序的交换次数要远远少于冒泡排序,平均性能优于冒泡排序。
最好、最坏、平均时间复杂度:O(n^2);
空间复杂度:O(1);
选择排序属于不稳定排序。
3. 堆排序
public class HeapSort {
int size;
private static final int DEFAULT_CAPACITY = 10;
int[] elements;
// 传入一个数组叫你批量建队,当然也传入了一个比较器!
public HeapSort(int[] elements) {
if (elements == null || elements.length == 0) {
this.elements = new int[DEFAULT_CAPACITY]; //没有传数组过来,就按照默认的办法做!
} else {
size = elements.length; //现在是将数据一次性直接拷贝过来,那么size的值也就是一次性赋值的!
int capacity = Math.max(elements.length, DEFAULT_CAPACITY); //保证有DEFAULT_CAPACITY的大小!
this.elements = new int[capacity];
for (int i = 0; i < elements.length; i++) {
this.elements[i] = elements[i]; //将数据放到二叉堆中的数组中但还是乱七八糟的,成员变量和形参名一样,用this区分!
}
heapify();
}
}
private void heapify() {
for (int i = (size >> 1) - 1; i >= 0; i--) {
// 自下而上的下滤
siftDown(i);
}
}
public void siftDown(int index) {
int element = elements[index];
int half = size >> 1;
while (index < half) {
int childIndex = index * 2 + 1;
int child = elements[childIndex];
int rightChildIndex = childIndex + 1;
if (rightChildIndex <= size - 1 && elements[rightChildIndex] > elements[childIndex]) {
child = elements[childIndex = rightChildIndex];
}
if (child <= element) {
break;
}
elements[index] = child;
index = childIndex;
}
elements[index] = element;
}
public void add(int element) {
if (size == 0) {
elements[size++] = element;
} else {
elements[size++] = element;
siftUp(size - 1);
}
}
private void siftUp(int index) {
int element = elements[index];
// 上滤到根节点
while (index > 0) {
// 得到父节点索引
int parentIndex = (index - 1) >> 1;
int parent = elements[parentIndex];
if (element <= parent) {
break;
}
elements[index] = parent;
index = parentIndex;
}
elements[index] = element;
}
// 默认建立的堆是大顶堆,那么此时堆顶就是最大的元素,将堆顶元素和最后一个元素交换,然后让堆的size - 1。
public void sort() {
int temp = 0;
while (size > 1) {
temp = elements[0];
elements[0] = elements[size - 1];
elements[size - 1] = temp;
size--;
siftDown(0);
}
}
public static void main(String[] args) {
int[] array = new int[]{4, 2, 85, 55, 47, 96};
HeapSort heap = new HeapSort(array);
heap.sort();
for (int i = 0; i < heap.elements.length; i++) {
System.out.println(heap.elements[i]);
}
}
}
4. 插入排序
插入排序非常类似于扑克牌的排序,将后面的牌一张张插入到前面,使得前面有序的牌逐渐变多,直到完全有序。
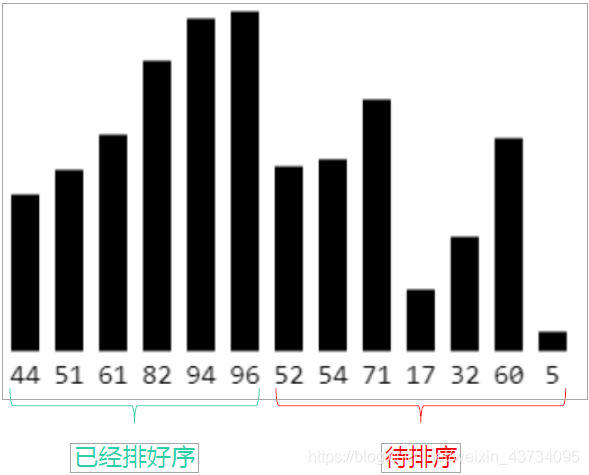
执行流程
- 在执行过程中,插入排序会将序列分为 2 部分头部是已经排好序的,尾部是待排序的;
- 从头开始扫描每一个元素,每当扫描到一个元素,就将它插入到头部合适的位置,使得头部数据依然保持有序。
什么是逆序对?
- 数组 <2, 3, 8, 6, 1> 的逆序对为:
< 2,1 > < 3,1> <8,1> <8,6> <6,1>,共5个逆序对。
插入排序的时间复杂度与逆序对的数量成正比关系。
- 逆序对的数量越多,插入排序的时间复杂度越高
public class Test {
public static void main(String[] args) {
int[] nums = new int[]{10, 9, 8, 7, 6, 5, 4, 3, 2, 1};
insertSort(nums);
for (int num : nums) {
System.out.println(num);
}
}
public static int[] insertSort(int[] nums) {
for (int i = 1; i < nums.length; i++) {
int cur = i;
// 不停的往后判断发现,当前值比前一个值小时,就交换这两个位置的值。
while (cur > 0 && nums[cur] < nums[cur - 1]) {
int temp = nums[cur];
nums[cur] = nums[cur - 1];
nums[cur - 1] = temp;
cur--;
}
}
return nums;
}
}
public class Test {
public static void main(String[] args) {
int[] nums = new int[]{10, 9, 8, 7, 6, 5, 4, 3, 2, 1};
insertSort(nums);
for (int num : nums) {
System.out.println(num);
}
}
public static int[] insertSort(int[] nums) {
for (int i = 1; i < nums.length; i++) {
int cur = i;
int insertNum = nums[cur];
while (cur >= 1 && insertNum < nums[cur - 1]) {
// 将交换替换为挪动
// 头部有序数据中比待插入元素大的,都朝尾部方向挪动1个位置
nums[cur] = nums[cur - 1];
cur--;
}
// 将待插入元素放到最终的合适位置
nums[cur] = insertNum;
}
return nums;
}
}
复杂度与稳定性
- 最坏、平均时间复杂度:O(n^2);
- 最好时间复杂度:O(n);
- 空间复杂度:O(1);
- 属于稳定排序;
- 当逆序对的数量极少时,插入排序的效率特别高,甚至速度比 O(nlogn) 级别的快速排序还要快。
5. 归并排序
public class Test {
// 用于辅助合并有序数组
private static int[] temp;
public int[] sortArray(int[] nums) {
int len = nums.length;
// 原数组的一半长度的temp数组
temp = new int[len >> 1];
sort(nums, 0, len - 1);
return nums;
}
private void sort(int[] nums, int left, int right) {
// 思考为什么递归出口是left == right?
// 看似一个很简单的问题,但是一时间想不明白,这很可能造成,面试写算法题时卡壳。
// 因为归并排序就是要将元素一直细分到每一组只有一个元素为止,此时 left == right。
if (left == right) {
return;
}
int mid = left + (right - left) / 2;
// 中间节点和前面部分在一起
sort(nums, left, mid);
sort(nums, mid + 1, right);
merge(nums, left, mid, right);
}
// 将 nums[left..mid] 和 nums[mid+1..right] 这两个有序数组合并成一个有序数组
private void merge(int[] nums, int left, int mid, int right) {
int li = 0;
int le = mid - left;
int ri = mid + 1;
int re = right;
// 注意ai每次的开始位置是当前要合并的两部分,左边部分的起始下标。
int ai = left;
// 备份原数组左半部分,方便在原数组上进行合并。
for (int i = li; i <= le; i++) {
temp[i] = nums[left + i];
}
// 只要备份数组中的数据处理完,左右两部分就合并完了。
while (li <= le) {
if (ri > re || temp[li] < nums[ri]) {
nums[ai++] = temp[li++];
} else {
nums[ai++] = nums[ri++];
}
}
}
public static void main(String[] args) {
// int[] nums = new int[]{10, 9, 8, 7, 6, 5, 4, 3, 2, 1};
int[] nums = new int[]{3, 8, 6, 10};
Test test = new Test();
int[] res = test.sortArray(nums);
for (int num : res) {
System.out.println(num);
}
}
}
6. 快速排序
初始快速排序代码:

用begin指向数组第一个元素,用end指向数组最后一个元素。
我们定义:
[begin + 1, j] 这个区间的元素都小于等于pivot轴点元素;
(j, i) 之间的元素都大于pivot轴点元素。
当i索引处对应的值小于等于pivot时,将i与第二个区间的第一个元素交换。也就是将i处的值与j++处的值交换
当i索引处对应的值大于pivot时,不需要交换,继续遍历i。代码如下:
public class Test1 {
static int[] nums;
public static void main(String[] args) {
nums = new int[]{6, 8, 10, 2, 1, 4, 9, 5, 7, 3};
sort();
for (int num : nums) {
System.out.println(num);
}
}
public static void sort() {
sort(0, nums.length - 1);
}
public static void sort(int begin, int end) {
if (end <= begin) {
return;
}
int mid = pivotIndex(begin, end);
sort(begin, mid - 1);
sort(mid + 1, end);
}
private static int pivotIndex(int begin, int end) {
// 先让begin位置的元素和随机元素交换。
int random = (int) (Math.random() * (end - begin));
swap(begin, begin + random);
// 备份轴点元素
int pivot = nums[begin];
int j = begin;
// 一边遍历,一边整理
// all in nums [begin + 1, j] <= pivot循环不变量的思想,值是在变的,但是值的定义没有变。比如j一直代表第一个区间的最后一个元素的索引下标
// all in nums (j, i) > pivot
for (int i = begin + 1; i <= end; i++) {
if (nums[i] <= pivot) {
// 因为我们定义j是第一个区间的最后一个元素,所以要将一个数加入到第一个区间。
// 将这个数和第二个区间的第一个数交换就行了,j此时就是第二个区间的第一个数的索引下标
j++;
swap(i, j);
}
}
// 将切分元素和第一个区间的最后一个元素交换
swap(begin, j);
return j;
}
private static void swap(int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
但是第一版代码存在的问题是如果待排序的数中有很多相同的数时,随机选择切分元素无效,这时候可以考虑双路排序。
/**
* 双路快排
*/
public class Test2 {
static int[] nums;
public static void main(String[] args) {
nums = new int[]{6, 8, 10, 2, 1, 4, 9, 5, 7, 3};
sort();
for (int num : nums) {
System.out.println(num);
}
}
public static void sort() {
sort(0, nums.length - 1);
}
public static void sort(int begin, int end) {
if (end <= begin) {
return;
}
int mid = pivotIndex(begin, end);
sort(begin, mid - 1);
sort(mid + 1, end);
}
public static int pivotIndex(int begin, int end) {
// 先让begin位置的元素和随机元素交换。
int random = (int) (Math.random() * (end - begin));
swap(begin, bgein + random);
// 备份轴点元素
int pivot = nums[begin];
while (begin < end) {
// 从右到左找比当前轴点元素小的
while (begin < end) {
if (nums[end] < pivot) {
nums[begin++] = nums[end];
break;
} else { // 大于等于就移动end
end--;
}
}
while (begin < end) {
if (nums[begin] > pivot) {
nums[end--] = nums[begin];
break;
} else {
begin++;
}
}
}
// 当begin == end 退出循环时,将轴点元素放到对应位置。
nums[begin] = pivot;
return begin;
}
public static void swap(int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
双路快排的思想是把严格小于和严格大于pivot的元素移动到两边,把等于pivot的元素挤向中间。
下面三路快排的思想是把全部区间分为3部分,第一部分是严格小于轴点元素的,第二部分是等于pivot元素的,第三部分是大于中间元素的。
双路快排是不去处理等于pivot元素的值,三路快排是主动去处理等于pivot的值。
public class Test3 {
static int[] nums;
public static void main(String[] args) {
nums = new int[]{6, 8, 10, 2, 1, 4, 9, 5, 7, 3};
sort();
for (int num : nums) {
System.out.println(num);
}
}
public static void sort() {
sort(0, nums.length - 1);
}
public static void sort(int begin, int end) {
if (end <= begin) {
return;
}
int random = (int) (Math.random() * (end - begin));
swap(begin, begin + random);
int pivot = nums[begin];
int lt = begin + 1;
int gt = end;
int i = begin + 1;
// all nums in [begin + 1, lt) < pivot [begin + 1, lt - 1]
// all nums in [lt, i) = pivot [lt, i - 1]
// all nums in (gt, end] > pivot [gt + 1, end]
while (i <= gt) {
if (nums[i] < pivot) {
// 将i索引位置元素和lt索引位置元素交换,lt索引位置就是第二个区间的第一个位置。
swap(i, lt);
lt++;
i++;
} else if (nums[i] == pivot) {
i++;
} else if (nums[i] > pivot) {
swap(i, gt);
gt--;
// 这里不能i++,因为交换过来的数还要进行判断。
}
}
swap(begin, lt - 1);
sort(begin, lt - 2);
sort(gt + 1, end);
}
private static void swap(int begin, int end) {
int temp = nums[begin];
nums[begin] = nums[end];
nums[end] = temp;
}
}
7. 希尔排序
希尔排序把序列看作是一个矩阵,分成 𝑚 列,逐列进行排序。
- 𝑚 从某个整数逐渐减为1;
- 当 𝑚 为1时,整个序列将完全有序。
因此,希尔排序也被称为递减增量排序(Diminishing Increment Sort)。
矩阵的列数取决于步长序列(step sequence):
- 不同的步长序列,执行效率也不同
希尔本人给出的步长序列是 𝑛 / 2^𝑘,比如 𝑛 为16时,步长序列是 { 1, 2, 4, 8 }。
假设有如下序列:{ 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1 }。

按照步长序列,首先分为8列,对每一列进行排序:
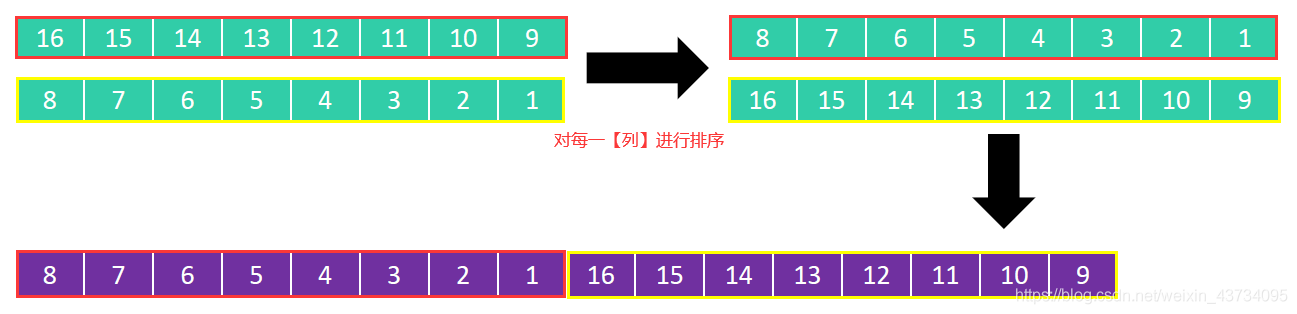
然后分为4列,对每一列进行排序:
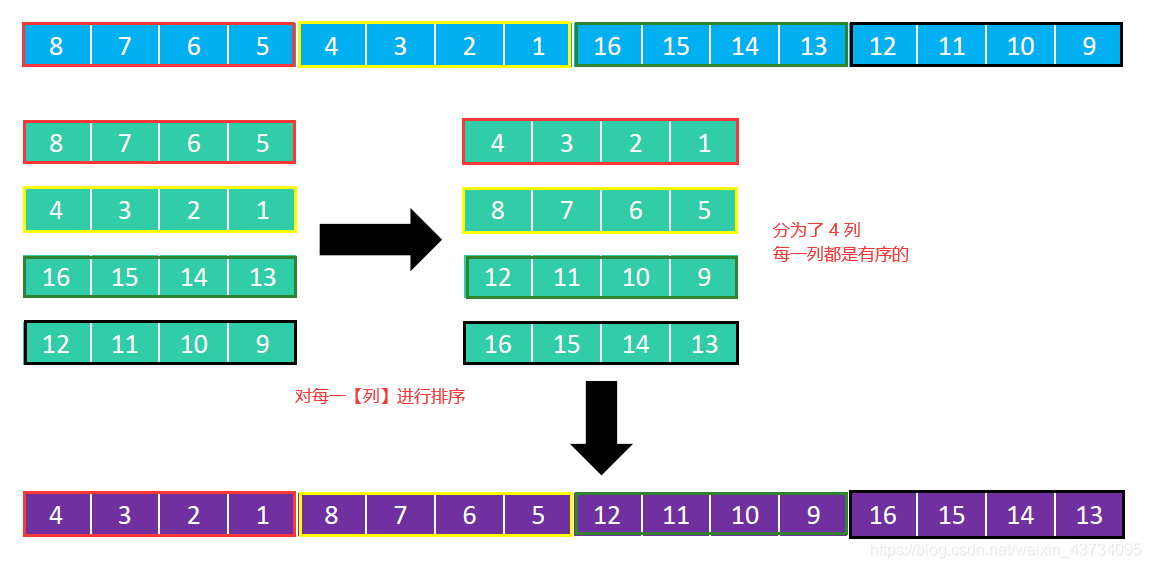
然后分为 2 列,对每一列进行排序:
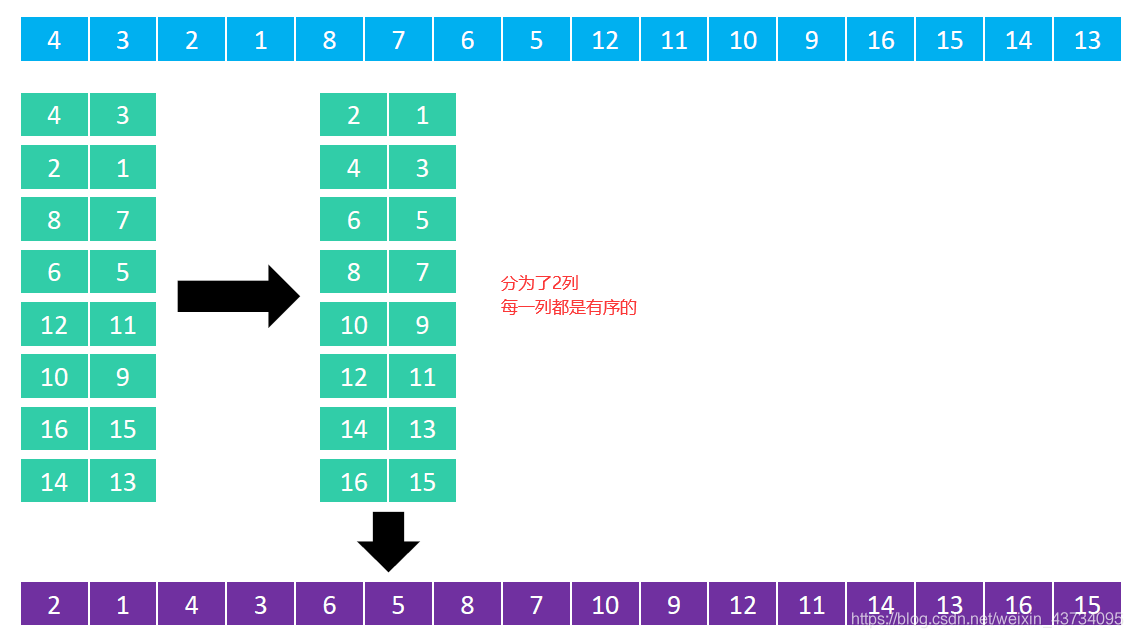
最后分为 1 列,变成升序序列。
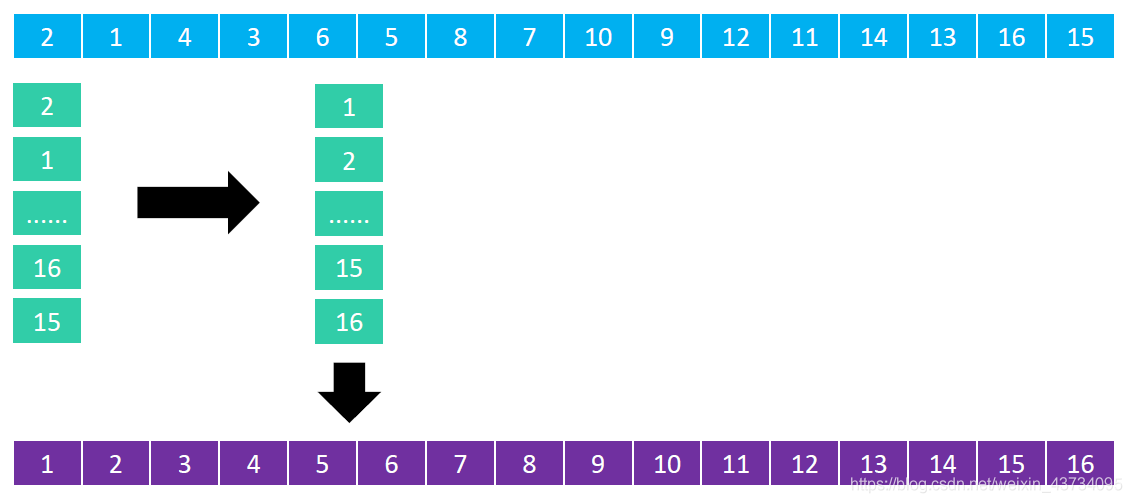
不难看出来,从8列变为1列的过程中,逆序对的数量在逐渐减少。
还记得插入排序的这个性质吗:
- 插入排序的时间复杂度与逆序对的数量成正比关系,逆序对的数量越多,插入排序的时间复杂度越高。
因此希尔排序底层一般使用插入排序对每一列进行排序,可以认为希尔排序是插入排序的改进版。
列的划分思路:
假设有11个元素,步长序列是 {1, 2, 5}
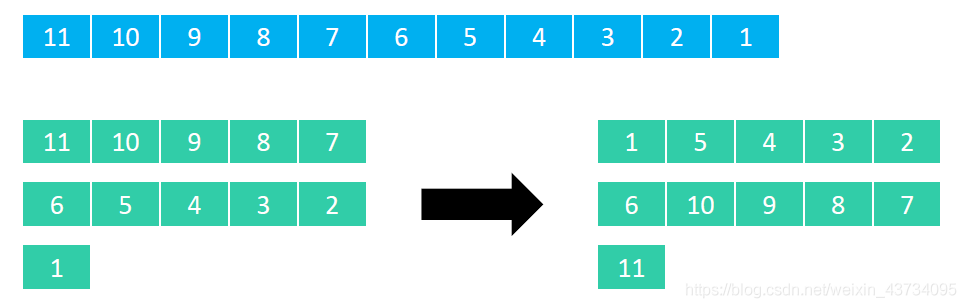
假设元素在第 col 列、第 row 行,步长(总列数)是 step。
那么这个元素在数组中的索引是 row * step + col。
- 比如 9 在排序前是第 0 行、第 2 列,那么它排序前的索引是 0 * 5 + 2 = 2;
- 比如 4 在排序前是第 1 行、第 2 列,那么它排序前的索引是 1 * 5 + 2 = 7。
public class Test {
static int[] nums;
public static void main(String[] args) {
nums = new int[]{6, 8, 10, 2, 1, 4, 9, 5, 7, 3};
Test test = new Test();
test.sort();
for (int num : nums) {
System.out.println(num);
}
}
private void sort() {
// 构建步长序列
List<Integer> stepSequence = shellStepSequence();
// 对每一个步长进行一次排序
for (int step : stepSequence) {
sort(step);
}
}
private void sort(int step) {
// 传进来的step代表有多少列,有多少列就进行多少次插入排序。
for (int col = 0; col < step; col++) {
for (int begin = col + step; begin < nums.length; begin = begin + step) {
int cur = begin;
while (cur > col && nums[cur] < nums[cur - step]) { // 用的插入排序
int temp = nums[cur];
nums[cur] = nums[cur - step];
nums[cur - step] = temp;
cur = cur - step;
}
}
}
}
// 希尔本人给出的步长序列是 𝑛/2^𝑘
private List<Integer> shellStepSequence() {
List<Integer> stepSequence = new ArrayList<>();
int step = nums.length;
while ((step >>= 1) > 0) {
stepSequence.add(step);
}
return stepSequence;
}
}
复杂度和稳定性
- 最好情况是步长序列只有1,且序列几乎有序,时间复杂度为 O(n);
- 最坏和平均时间复杂度取决步长序列, 范围在 O(n3/4) ~ O(n2);
- 空间复杂度为O(1);
- 希尔排序属于不稳定排序。
Rabin-Karp算法
3、刷题
模拟
29. 两数相除
给定两个整数,被除数 dividend 和除数 divisor。将两数相除,要求不使用乘法、除法和 mod 运算符。
返回被除数 dividend 除以除数 divisor 得到的商。
整数除法的结果应当截去(truncate)其小数部分,例如:truncate(8.345) = 8 以及 truncate(-2.7335) = -2
32. 最长有效括号子串的长度⭐⭐⭐🎯
给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
输入:s = "(()"
输出:2
解释:最长有效括号子串是 "()"
输入:s = ")()())"
输出:4
解释:最长有效括号子串是 "()()"
class Solution {
public int longestValidParentheses(String s) {
Stack<Integer> stack = new Stack<>();
int n = s.length();
int res = 0, start = 0;
for (int i = 0; i < n; i++) {
if (s.charAt(i) == '(') {
// 把左括号索引放入栈中。
stack.push(i);
continue;
}
// 遇到右括号时,栈不为空。
if (!stack.isEmpty()) {
stack.pop();
if (stack.isEmpty()) {
res = Math.max(res, i - start + 1);
} else {
res = Math.max(res, i - stack.peek());
}
} else {
// 遇到右括号时栈还为空。
// 则当前的 start 开始的子串不再可能为合法子串了,下一个合法子串的起始位置可能是 i + 1,更新 start = i + 1。
start = i + 1;
}
}
return res;
}
}
71. 简化路径⭐
给你一个字符串 path ,表示指向某一文件或目录的 Unix 风格 绝对路径 (以 '/' 开头),请你将其转化为更加简洁的规范路径。
在 Unix 风格的文件系统中,一个点(.)表示当前目录本身;此外,两个点 (..) 表示将目录切换到上一级(指向父目录);两者都可以是复杂相对路径的组
成部分。任意多个连续的斜杠(即,'//')都被视为单个斜杠 '/' 。 对于此问题,任何其他格式的点(例如,'...')均被视为文件/目录名称。
请注意,返回的 规范路径 必须遵循下述格式:
- 始终以斜杠 '/' 开头。
- 两个目录名之间必须只有一个斜杠 '/' 。
- 最后一个目录名(如果存在)不能 以 '/' 结尾。
- 此外,路径仅包含从根目录到目标文件或目录的路径上的目录(即,不含 '.' 或 '..')。
返回简化后得到的 规范路径 。
https://leetcode.cn/problems/simplify-path/solution/71-jian-hua-lu-jing-zhan-de-ying-yong-yu-ikxq/
class Solution {
public String simplifyPath(String path) {
// 将路径按照/分割
String[] dirs = path.split("/");
Stack<String> stack = new Stack<>();
for (String str : dirs) {
// 遇到空字符和.就跳过
if ("".equals(str) || ".".equals(str)) {
continue;
}
// 遇到..就从栈里面弹出一个元素
if ("..".equals(str)) {
if (!stack.isEmpty()) {
stack.pop();
}
// 直接开始处理下一个,别再把..放入栈中
continue;
}
// 除去上面几种类型的字符其余都放入栈中。
stack.push(str);
}
StringBuilder sb = new StringBuilder();
if (stack.isEmpty()) {
sb.insert(0, "/");
} else {
while (!stack.isEmpty()) {
sb.insert(0, stack.pop());
sb.insert(0, "/");
}
}
return sb.toString();
}
}
89. 格雷编码
n 位格雷码序列 是一个由 2^n 个整数组成的序列,其中:
- 每个整数都在范围 [0, 2^n - 1] 内(含 0 和 2^n - 1)
- 第一个整数是 0
- 一个整数在序列中出现 不超过一次
- 每对 相邻 整数的二进制表示 恰好一位不同 ,且
- 第一个 和 最后一个 整数的二进制表示 恰好一位不同
给你一个整数 n ,返回任一有效的 n 位格雷码序列 。
参考题解:https://leetcode.cn/problems/gray-code/solution/jin-dao-ge-lei-ma-shi-zhe-yang-wan-de-by-qrx4/
如下图所示,我们可以看出格雷码的一些规律:
n=1位格雷码有两个码字(0和1)
n位格雷码中的前(n-1)^2个码字等于n-1位格雷码的码字,按顺序书写,加前缀0
n位格雷码中的后(n-1)^2个码字等于n-1位格雷码的码字,按逆序书写,加前缀1
n位格雷码的集合 = n-1位格雷码集合(顺序)加前缀0 + n-1位格雷码集合(逆序)加前缀1
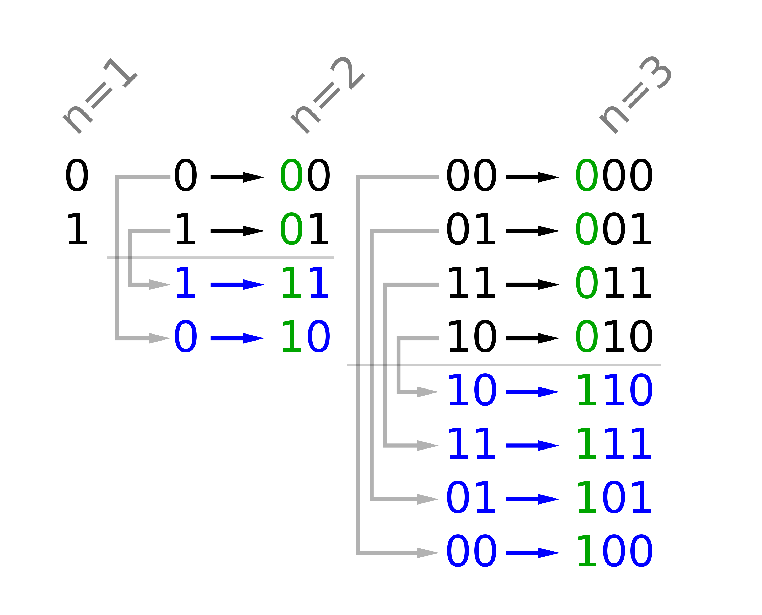
class Solution {
public List<Integer> grayCode(int n) {
List<Integer> result = new ArrayList<>();
result.add(0);
result.add(1);
int mask = 1 << 1; // 二进制:10
for (int i = 2; i <= n; i++) { // 我们从n=2来计算格雷码
// 倒序访问,高位置1
for (int j = result.size() - 1; j >= 0; j--) {
result.add(mask | result.get(j));
}
mask = mask << 1;
}
return result;
}
}
150. 逆波兰表达式求值
根据 逆波兰表示法,求表达式的值。
有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
注意 两个整数之间的除法只保留整数部分。
可以保证给定的逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
class Solution {
public int evalRPN(String[] tokens) {
Deque<Integer> stack = new LinkedList<>();
int n = tokens.length;
for (int i = 0; i < n; i++) {
String token = tokens[i];
// 判断是否是数字
if (Character.isDigit(token.charAt(0))) {
// 是数字就放到栈中
stack.push(Integer.parseInt(token));
} else {
// 当扫描到非数字时就说明需要进行运算,需要进行出栈操作。
int number2 = stack.pop();
int number1 = stack.pop();
// 根据扫描到的运算符进行相应的运算。并且将运算结果又重新放回栈中。
switch (token) {
case "+":
stack.push(number1 + number2);
// 一定要加break,不然会继续往下执行case语句。
break;
case "-":
stack.push(number1 - number2);
break;
case "*":
stack.push(number1 * number2);
break;
case "/":
stack.push(number1 / number2);
break;
}
}
}
return stack.pop();
}
/**
* 因为这个字符串数组中只有四种运算符和数字,只要不是四种运算符中的一种那么就是数字咯。
*
* @param token
* @return
*/
public boolean isNumber(String token) {
return !("+".equals(token) || "-".equals(token) || "*".equals(token) || "/".equals(token));
}
}
224. 基本计算器⭐⭐
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
注意:不允许使用任何将字符串作为数学表达式计算的内置函数,比如 eval() 。
参考题解:https://labuladong.gitee.io/algo/4/33/128/
class Solution {
public int calculate(String s) {
Deque<Character> q = new LinkedList<>();
for (char c : s.toCharArray()) {
q.offer(c);
}
return dfs(q);
}
public int dfs(Deque<Character> q) {
Stack<Integer> stack = new Stack<>();
// 当前运算符的前一个运算符
char op = '+';
// op后面的数
int num = 0;
int res = 0;
while (!q.isEmpty()) {
char c = q.poll();
// c是数字就更新数字
if (Character.isDigit(c)) {
num = num * 10 + (c - '0');
}
// 左括号就进入递归
if (c == '(') {
num = dfs(q);
}
// c是运算符,之前的数字和符号放进栈中。
if (!Character.isDigit(c) && c != ' ' || q.isEmpty()) {
if (op == '+') {
stack.push(num);
} else if (op == '-') {
stack.push(-num);
} else if (op == '*') {
// 弹出栈顶元素做乘法运算
stack.push(stack.pop() * num);
} else if (op == '/') {
// 弹出栈顶元素做除法运算
stack.push(stack.pop() / num);
}
num = 0;
op = c;
}
// 是右括号就退出循环,直接返回结果。
if (c == ')') {
break;
}
}
// 将栈中所有结果求和。
for (int i : stack) {
res += i;
}
return res;
}
}
227. 基本计算器 II⭐⭐
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
整数除法仅保留整数部分。
你可以假设给定的表达式总是有效的。所有中间结果将在 [-231, 231 - 1] 的范围内。
注意:不允许使用任何将字符串作为数学表达式计算的内置函数,比如 eval() 。
输入:s = "3+2*2"
输出:7
class Solution {
public int calculate(String s) {
LinkedList<Character> queue = new LinkedList<>();
for (Character ch : s.toCharArray()) {
queue.offer(ch);
}
return dfs(queue);
}
public int dfs(LinkedList<Character> queue) {
int num = 0, res = 0;
char op = '+';
Stack<Integer> stack = new Stack<>();
while (!queue.isEmpty()) {
char ch = queue.poll();
if (Character.isDigit(ch)) {
num = num * 10 + (ch - '0');
}
if (!Character.isDigit(ch) && ch != ' ' || queue.isEmpty()) {
if (op == '+') {
stack.push(num);
} else if (op == '-') {
stack.push(-num);
} else if (op == '*') {
stack.push(stack.pop() * num);
} else if (op == '/') {
stack.push(stack.pop() / num);
}
num = 0;
op = ch;
}
}
for (int i : stack) {
res += i;
}
return res;
}
}
772. 基本计算器III⭐⭐
实现一个基本的计算器来计算简单的表达式字符串。
表达式字符串只包含非负整数,算符+、-、*、/,左括号(和右括号)。
这题是会员题,不知道题目是怎么样的,那么我们就给它加上匹配括号吧,运算符有加减乘除。
class Solution {
public int calculate(String s) {
LinkedList<Character> queue = new LinkedList<>();
for (Character ch : s.toCharArray()) {
queue.offer(ch);
}
return dfs(queue);
}
public int dfs(LinkedList<Character> queue) {
int num = 0, res = 0;
char op = '+';
Stack<Integer> stack = new Stack<>();
while (!queue.isEmpty()) {
char ch = queue.poll();
if (Character.isDigit(ch)) {
num = num * 10 + (ch - '0');
}
if (ch == '(') {
num = dfs(queue);
}
if (!Character.isDigit(ch) && ch != ' ' || queue.isEmpty()) {
if (op == '+') {
stack.push(num);
} else if (op == '-') {
stack.push(-num);
} else if (op == '*') {
stack.push(stack.pop() * num);
} else if (op == '/') {
stack.push(stack.pop() / num);
}
num = 0;
op = ch;
}
if (ch == ')') {
break;
}
}
for (int i : stack) {
res += i;
}
return res;
}
}
258. 各位相加
给定一个非负整数 num,反复将各个位上的数字相加,直到结果为一位数。返回这个结果。
class Solution {
public int addDigits(int num) {
while (num > 9) {
int t = 0;
while (num != 0) {
t = t + num % 10;
num = num / 10;
}
num = t;
}
return num;
}
}
396. 旋转函数⭐
给定一个长度为 n 的整数数组 nums 。
假设 arrk 是数组 nums 顺时针旋转 k 个位置后的数组,我们定义 nums 的 旋转函数 F 为:
- F(k) = 0 * arrk[0] + 1 * arrk[1] + ... + (n - 1) * arrk[n - 1]
返回 F(0), F(1), ..., F(n-1)中的最大值 。
生成的测试用例让答案符合 32 位 整数。
向右旋转一次,就相当于把当前结果加上整个数组的和,再减去数组大小乘以当前最后一位。想到这个就很简单了
class Solution {
public int maxRotateFunction(int[] nums) {
int len = nums.length;
int sum = 0, pre = 0;
for (int i = 0; i < len; i++) {
sum += nums[i];
pre += i * nums[i];
}
int max = pre, temp = 0;
for (int i = len - 1; i >= 0; i--) {
pre = (pre + sum) - len * nums[i];
max = Math.max(max, pre);
}
return max;
}
}
846. 一手顺子⭐⭐⭐
Alice 手中有一把牌,她想要重新排列这些牌,分成若干组,使每一组的牌数都是 groupSize ,并且由 groupSize 张连续的牌组成。
给你一个整数数组 hand 其中 hand[i] 是写在第 i 张牌,和一个整数 groupSize 。如果她可能重新排列这些牌,返回 true ;否则,返回 false 。
921. 使括号有效的最少添加⭐⭐⭐🎯
只有满足下面几点之一,括号字符串才是有效的:
- 它是一个空字符串,或者
- 它可以被写成 AB (A 与 B 连接), 其中 A 和 B 都是有效字符串,或者
- 它可以被写作 (A),其中 A 是有效字符串。
给定一个括号字符串 s ,移动N次,你就可以在字符串的任何位置插入一个括号。
- 例如,如果 s = "()))" ,你可以插入一个开始括号为 "(()))" 或结束括号为 "())))" 。
返回 为使结果字符串 s 有效而必须添加的最少括号数。
class Solution {
int minAddToMakeValid(String s) {
// res 记录左括号插入次数
int res = 0;
// need 变量记录右括号的需求量
int need = 0;
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
// 对右括号的需求 + 1
need++;
}
// 如果先出现左括号,后出现右括号,一定会有一对配合的左右括号(),因为总有左括号到右括号的转折点。
if (s.charAt(i) == ')') {
// 对右括号的需求 - 1
need--;
if (need == -1) {
need = 0;
// 需插入一个左括号
res++;
}
}
}
return res + need;
}
}
1541. 平衡括号字符串的最少插入次数⭐⭐⭐🎯
给你一个括号字符串 s ,它只包含字符 '(' 和 ')' 。一个括号字符串被称为平衡的当它满足:
- 任何左括号 '(' 必须对应两个连续的右括号 '))' 。
- 左括号 '(' 必须在对应的连续两个右括号 '))' 之前。
比方说 "())", "())(())))" 和 "(())())))" 都是平衡的, ")()", "()))" 和 "(()))" 都是不平衡的。
你可以在任意位置插入字符 '(' 和 ')' 使字符串平衡。
请你返回让 s 平衡的最少插入次数。
class Solution {
public int minInsertions(String s) {
int n = s.length();
Stack<Character> stack = new Stack<>();
int ans = 0;
for (int i = 0; i < n; i++) {
// 遇到左括号直接入栈
if (s.charAt(i) == '(') {
stack.push(s.charAt(i));
continue;
}
// 遇到右括号
// 当前为最后一个字符
if (i + 1 == n) {
// 栈为空,里面没有左括号,为了使最后的这个)有效需要添加一个(和一个)。
if (stack.isEmpty()) {
ans += 2;
} else {
// 栈不为空,说明之前还有左括号没有参与匹配,只需要加一个)
stack.pop();
ans++;
}
} else {
// 当前i位置是),下一个位置i + 1也是)。
if (s.charAt(i + 1) == ')') {
if (stack.isEmpty()) {
ans++;
} else {
stack.pop();
}
// 因为把下一个右括号也匹配了。
// 这里i++,再加上for循环的i++,直接跳到i + 2位置。
i++;
} else { // 下一个字符不是右括号,是左括号。
if (stack.isEmpty()) {
ans += 2;
} else {
stack.pop();
ans++;
}
}
}
}
// 当栈中还存在没有匹配的左括号那么还需要两倍数量的右括号。
ans += stack.size() * 2;
return ans;
}
}
位运算
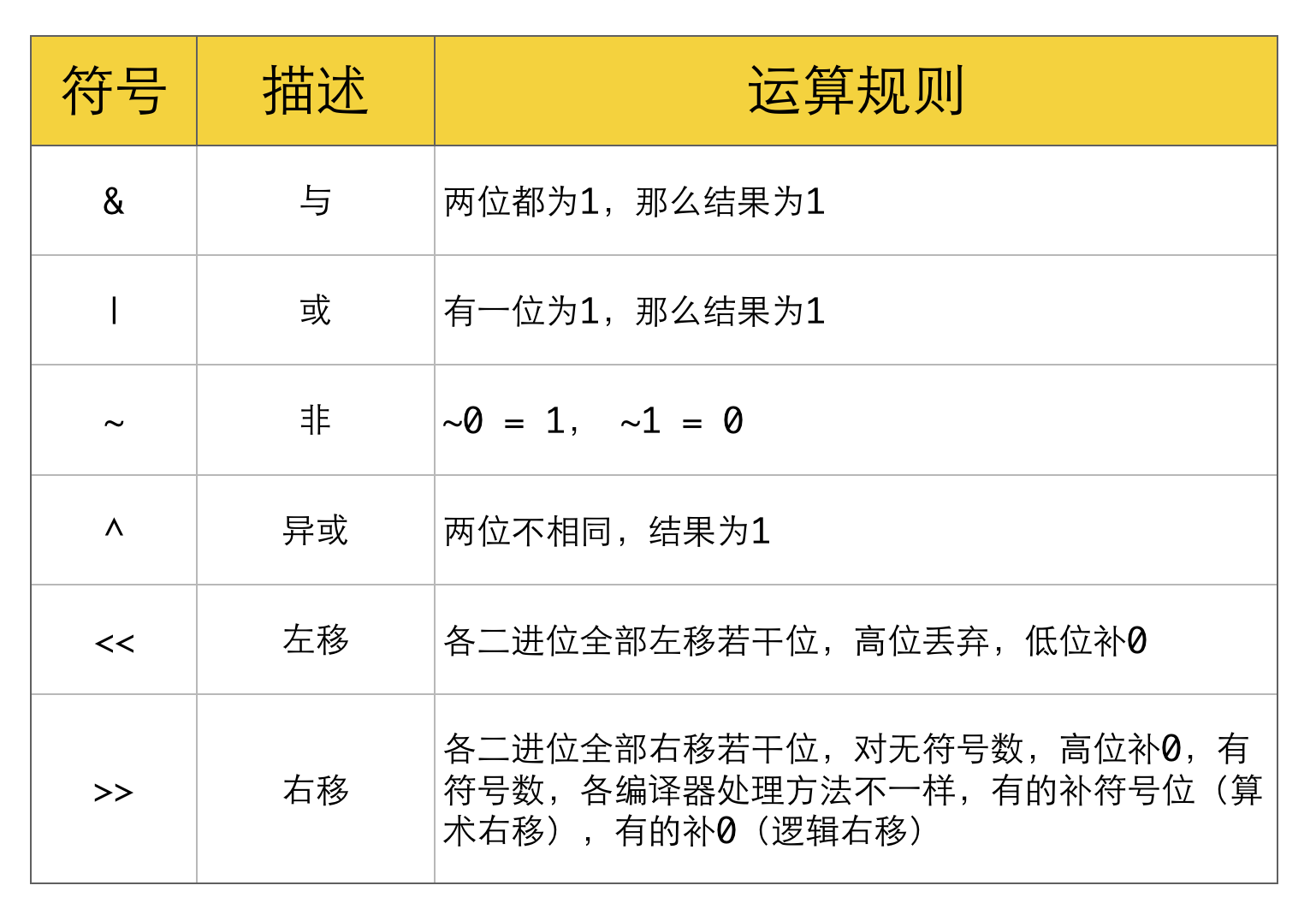
常见位操作
1、判断奇偶
(x & 1) == 1 等价于(x % 2) == 1;
(x & 1) == 0 等价于(x % 2) == 0。
2、x / 2 等价于 x >> 1
3、x = x & (x - 1) 等价于把x最低位的二进制1去掉
4、x & -x 得到最低位的1
5、x & ~x 等于0
191. 位1的个数(汉明重量)
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 '1' 的个数(也被称为汉明重量)。
位数检查解法:一个朴素的做法是,对 int 的每一位进行检查,并统计 1 的个数。
class Solution {
public int hammingWeight(int n) {
int res = 0;
for (int i = 0; i < 32; i++) {
// 不断地进行移位操作
res = res + ((res >> i) & 1)
}
return res;
}
}
一种时间复杂度更低的解法是 Brian Kernighan 算法。Brian Kernighan 算法的原理是:对于任意整数num,num & (num - 1)的结果是将num的二进制表示的最
后一个1变成0之后的整数,即num & (num - 1)比特1的个数比num比特1的个数少1个。对于给定的整数 num,计算 num & (num - 1)的值并将 num 的值更新为
该值,直到 num 变成 0,则操作次数为 num 的比特一的个数。
class Solution {
public int hammingWeight(int n) {
int res = 0;
while (n != 0) {
n = n & (n - 1);
res++;
}
return res;
}
}
338. 比特位计数
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
这道题和191题实际上是一样的。
class Solution {
public int[] countBits(int n) {
int[] res = new int[n + 1];
for (int i = 0; i <= n; i++) {
int num = i;
while (num != 0) {
num = num & (num - 1);
res[i]++;
}
}
return res;
}
}
461. 汉明距离⭐⭐
两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。
给你两个整数 x 和 y,计算并返回它们之间的汉明距离。
输入:x = 1, y = 4
输出:2
解释:
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
上面的箭头指出了对应二进制位不同的位置。
第一种解法:
class Solution {
public int hammingDistance(int x, int y) {
// 两个数异或之后,再求二进制位1地个数。
int result = Count1(x ^ y);
return result;
}
public int Count1(int n) {
int res = 0;
while (n != 0) {
n = n & (n - 1);
res++;
}
return res;
}
}
第二种解法:
class Solution {
public int hammingDistance(int x, int y) {
int ans = 0;
for (int i = 0; i < 32; i++) {
// 对x和y这两个数一位一位的进行异或
int a = (x >> i) & 1 , b = (y >> i) & 1;
ans += (a ^ b);
}
return ans;
}
}
476. 数字的补数
对整数的二进制表示取反(0 变 1 ,1 变 0)后,再转换为十进制表示,可以得到这个整数的补数。
例如,整数 5 的二进制表示是 "101" ,取反后得到 "010" ,再转回十进制表示得到补数 2 。
给你一个整数 num ,输出它的补数。
class Solution {
public int findComplement(int num) {
int s = -1;
// 找到最高位的1
for (int i = 31; i >= 0; i--) {
if (((num >> i) & 1) != 0) {
s = i;
break;
}
}
int ans = 0;
// 从最低位开始判断0的位
for (int i = 0; i <= s; i++) {
if (((num >> i) & 1) == 0) {
ans = ans + (1 << i);
}
}
return ans;
}
}
136. 只出现一次的数字
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
/**
* 异或操作是两个二进制位相同为0,不同为1。
*/
class Solution {
public int singleNumber(int[] nums) {
int single = 0;
for (int num : nums) {
single ^= num;
}
return single;
}
}
477. 汉明距离总和⭐⭐
两个整数的 汉明距离 指的是这两个数字的二进制数对应位不同的数量。
给你一个整数数组 nums,请你计算并返回 nums 中任意两个数之间 汉明距离的总和 。
思路:逐位统计。
逐位统计这四个字非常好的概括了这个方法,统计所有数字每一位1与0的个数,再通过计算得到总汉明距离。
“具体地,若长度为 n 的数组 nums 的所有元素二进制的第 i 位共有 c 个 1,n-c 个 0,则些元素在二进制的第 i 位上的汉明距离之和为c⋅(n−c)”。
对于每个1来说,与0的汉明距离都是1,与1的汉明距离为0,有c个1,n-c个0,所以该位的总汉明距离是c⋅(n−c)。
class Solution {
public int totalHammingDistance(int[] nums) {
int n = nums.length;
int res = 0;
for (int i = 0; i < 32; i++) {
int c = 0;
for (int num : nums) {
c = c + ((num >> i) & 1);
}
res = res + c * (n - c);
}
return res;
}
}
137. 只出现一次的数字 II
给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。
输入:nums = [2,2,3,2]
输出:3
哈希解法:
class Solution {
public int singleNumber(int[] nums) {
Map<Integer, Integer> map = new HashMap<>();
for (int x : nums) {
map.put(x, map.getOrDefault(x, 0) + 1);
}
for (int x : map.keySet()) {
if (map.get(x) == 1) {
return x;
}
}
return -1;
}
}
位运算解法:
class Solution {
public int singelNumber(int[] nums) {
int[] cnt = new int[32];
for (int num : nums) {
for (int i = 0; i < 32; i++) {
if (((num >> i) & 1) == 1) {
cnt[i]++;
}
}
}
int ans = 0;
for (int i = 0; i < 32; i++) {
if (cnt[i] % 3 == 1) {
ans = ans + 1 << i;
}
}
return ans;
}
}
260. 只出现一次的数字 III⭐⭐⭐
给定一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。
解题思路:
利用除答案以外的元素均出现两次,我们可以先对 nums 中的所有元素执行异或操作,得到 sumsum,sumsum 为两答案的异或值(sum 必然不为
00)。然后取 sum 二进制表示中为 1 的任意一位 k,sum 中的第 k 位为 1 意味着两答案的第 k 位二进制表示不同。
对 nums 进行遍历,对第 k 位分别为 0 和 1 的元素分别求异或和(两答案必然会被分到不同的组),即为答案。
class Solution {
public int[] singleNumber(int[] nums) {
int sum = 0;
for (int i : nums) {
sum ^= i;
}
int k = -1;
for (int i = 31; i >= 0 && k == -1; i--) {
if (((sum >> i) & 1) == 1) {
k = i;
}
}
// 不同的两个数在第k位不一样,会被分到不同的组。
// 两个相同的数在第k位一样,分到同一个组,每个组的元素进行异或,剩下的就是只出现一次的数字。
int[] ans = new int[2];
for (int i : nums) {
if (((i >> k) & 1) == 1) {
ans[1] ^= i;
} else {
ans[0] ^= i;
}
}
return ans;
}
}
268. 丢失的数字⭐⭐
给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。
解题思路:
找缺失数、找出现一次数都是异或的经典应用。
我们可以先求得 [1, n] 的异或和 ans,然后用 ans 对各个 nums[i] 进行异或。
这样最终得到的异或和表达式中,只有缺失元素出现次数为 11 次,其余元素均出现两次(x⊕x=0),即最终答案 ans 为缺失元素。
class Solution {
public int missingNumber(int[] nums) {
// 数组长度为n,说明nums数组中存储的元素是属于[0, n]的。
int n = nums.length;
int ans = 0;
for (int i = 0; i <= n; i++) {
ans = ans ^ i;
}
for (int num : nums) {
ans = ans ^ num;
}
return ans;
}
}
190. 颠倒二进制位⭐⭐
颠倒给定的 32 位无符号整数的二进制位。
提示:请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
在 Java 中,编译器使用二进制补码记法来表示有符号整数。因此,在 示例 2 中,输入表示有符号整数 -3,输出表示有符号整数 -1073741825。
class Solution {
public int reverseBits(int n) {
int res = 0;
for (int i = 0; i < 32; i++) {
if (((n >> i) * 1) == 1) {
res = res + (1 << (31 - i));
}
}
return res;
}
}
371. 两整数之和⭐⭐⭐
不用加号和减号计算两个整数之和
carry表示进位
当 a = 0 时,a + b = b,返回 b 即可。
当 a ≠ 0 时,考虑两个二进制数之和的最简单形式:0 + 0 = 0,0 + 1 = 1,1 + 0 = 1,1 + 1 = 10。
两整数之和的进位部分等于两整数按位与运算左移一位的结果,两整数之和的非进位部分等于两整数按位异或运算的结果。
因此,a + b 可以表示成进位部分与非进位部分之和,用 (a & b) << 1和 (a ^ b)的值更新a和b的值。
由于不允许使用加号和减号,因此更新 a 和 b 的值之后仍不能返回 a+b,而是需要重复上述操作更新 a 和 b 的值,直到 a=0,此时两整数之和是 b。
class Solution {
public int getSum(int a, int b) {
int carry;
int remain;
// 当进位a不等于0就继续加
while (a != 0) {
// 进位
carry = (a & b) << 1;
remain = a ^ b;
a = carry;
b = remain;
}
return b;
}
}
231. 2 的幂⭐
给你一个整数 n,请你判断该整数是否是 2 的幂次方。如果是,返回 true ;否则,返回 false 。
如果存在一个整数 x 使得 n == 2^x ,则认为 n 是 2 的幂次方。
https://leetcode.cn/problems/power-of-two/solution/5chong-jie-fa-ni-ying-gai-bei-xia-de-wei-6x9m/
因为2的幂的二进制表示只有一个1其余全是0,所以我们判断到位1的个数是1,说明n是2的幂。
class Solution {
public boolean isPowerOfTwo(int n) {
return n > 0 && count1(n) == 1;
}
public int count1(int n) {
int res = 0;
while (n != 0) {
n = n & (n - 1);
res++;
}
return res;
}
}
class Solution {
public boolean isPowerOfTwo(int n) {
return n > 0 && (n & (n - 1)) == 1;
}
}
class Solution {
public bollean isPowerOfTwo(int n) {
return n > 0 && Integer.bitcount(n) == 1;
}
}
326. 3 的幂
给定一个整数,写一个函数来判断它是否是 3 的幂次方。如果是,返回 true ;否则,返回 false 。
整数 n 是 3 的幂次方需满足:存在整数 x 使得 n == 3^x。
解法一:打表
使用 static 代码块,预处理出不超过 int 数据范围的所有 3 的幂,这样我们在跑测试样例时,就不需要使用「循环/递归」来实现逻辑,可直接 O(1)查表返回。
class Solution {
static Set<Integer> set = new HashSet<>();
static {
int cur = 1;
set.add(cur);
while (cur <= Integer.MAX_VALUE / 3) {
cur *= 3;
set.add(cur);
}
}
public boolean isPowerOfThree(int n) {
return n > 0 && set.contains(n);
}
}
解法二:朴素解法
class Solution {
public boolean isPowerOfThree(int n) {
if (n <= 0) {
return false;
}
while ((n % 3) == 0) {
n = n / 3;
}
return n == 1;
}
}
342. 4的幂
给定一个整数,写一个函数来判断它是否是 4 的幂次方。如果是,返回 true ,否则,返回 false 。
整数 n 是 4 的幂次方需满足:存在整数 x 使得 n == 4^x。
n若是4的幂,那么肯定也是2的幂。然后判断 (n % 3) == 1 就能知道是不是4的幂。
解题思路:
理论上数字4幂的二进制类似于100,10000,1000000,etc...形式。可以有如下结论:
-
4的幂一定是2的;
-
4的幂和2的幂一样,只会出现一位1。但是,4的1总是出现在奇数位。
一旦判断了是2的幂了,就只需要区分到底是2还是4还是8。有人用,num % 3 == 1来判断num == 4,而不是num == 2。
这样是可行的,因为num % 3 == 1,就保证了num只能是4、16,etc。这些明显是4的幂。
扩展:
num%3==1 很厉害,由于 4=3+1, 那么4的N次方就是(3+1)^ N,尝试展开多项式,比如(3+1)^2 =(3+1) * (3+1),除了1 * 1以外永远都有3相乘,再展开3次方,
(3+1) * (3+1) * (3+1),结论一致,除了结尾的1都有3相乘,因此可以有结论,一个数的N次方-1总能除尽比这个数小1的数。
class Solution {
public boolean isPowerOfFour(int n) {
// 2的幂二进制位只有一位是1,所以说n & (n - 1)必定为0。
if (n < 0 || (n & (n - 1)) != 0) {
return false;
}
return (n % 3) == 1;
}
}
318. 最大单词长度乘积
693. 交替位二进制数
给定一个正整数,检查它的二进制表示是否总是 0、1 交替出现:换句话说,就是二进制表示中相邻两位的数字永不相同。
class Solution {
public boolean hasAlternatingBits(int n) {
// 如 010101 右移一位得到 001010
// 二者异或之后得到011111 (这一步是关键,只有交替出现01,异或后才能得到结果0111111...11)
// 为了判断 异或后的结果是否满足(0111111...11)类型的结果
// 可以用如下方法,比如
// 011111 加上1 为100000
// 011111 与 100000按位相与 结果为000000 , 也就是0;
int m = n ^ (n >> 1);
return (m & (m + 1)) == 0;
}
}
数学运算技巧
50. Pow(x, n)
实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,x^n )。
快速幂方法:https://leetcode.cn/problems/powx-n/solution/50-powx-n-kuai-su-mi-qing-xi-tu-jie-by-jyd/
Java 代码中 int32 变量 n∈[−2147483648,2147483647] ,因此当 n = -2147483648 时执行 n = -n会因越界而赋值出错。
解决方法是先将 n 存入 long 变量 b ,后面用 b 操作即可。
class Solution {
public int pow(int x, int n) {
long b = n;
if (b < 0) {
b = -b;
x = 1 / x;
}
double res = 1;
while (b > 0) {
if ((b & 1) == 1) {
res = res * x;
}
x = x * x;
b = b >> 1;
}
}
return res;
}
172. 阶乘后的零
给定一个整数 n ,返回 n! 结果中尾随零的数量。
提示 n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1。
解题思路:
肯定不可能真去把 n! 的结果算出来,阶乘增长可是比指数增长都恐怖,趁早死了这条心吧。
那么,结果的末尾的 0 从哪里来的?我们有没有投机取巧的方法计算出来?
首先,两个数相乘结果末尾有 0,一定是因为两个数中有因子 2 和 5,因为 10 = 2 x 5。
也就是说,问题转化为:n! 最多可以分解出多少个因子 2 和 5?
比如说 n = 25,那么 25! 最多可以分解出几个 2 和 5 相乘?
这个主要取决于能分解出几个因子 5,因为每个偶数都能分解出因子 2,因子 2 肯定比因子 5 多得多。
25! 中 5 可以提供一个,10 可以提供一个,15 可以提供一个,20 可以提供一个,25 可以提供两个,总共有 6 个因子 5,所以 25! 的结果末尾就有 6 个 0。
现在,问题转化为:n! 最多可以分解出多少个因子 5?
难点在于像 25,50,125 这样的数,可以提供不止一个因子 5,怎么才能不漏掉呢?
这样,我们假设 n = 125,来算一算 125! 的结果末尾有几个 0:
首先,125 / 5 = 25,这一步就是计算有多少个像 5,15,20,25 这些 5 的倍数,它们一定可以提供一个因子 5。
但是,这些足够吗?刚才说了,像 25,50,75 这些 25 的倍数,可以提供两个因子 5,那么我们再计算出 125! 中有 125 / 25 = 5 个 25 的倍数,它们每人可以额
外再提供一个因子 5。
够了吗?我们发现 125 = 5 x 5 x 5,像 125,250 这些 125 的倍数,可以提供 3 个因子 5,那么我们还得再计算出 125! 中有 125 / 125 = 1 个 125 的倍数,它还
可以额外再提供一个因子 5。
这下应该够了,125! 最多可以分解出 25 + 5 + 1 = 31 个因子 5,也就是说阶乘结果的末尾有 31 个 0。
理解了这个思路,就可以理解解法代码了:
class Solution {
public int trailingZeroes(int n) {
int count = 0;
long divisor = 5;
while (divisor <= n) {
count += n / divisor;
divisor = divisor * 5;
}
return count;
}
}
204. 计数质数⭐⭐⭐
给定整数 n ,返回所有小于非负整数 n 的质数的数量 。
参考题解:https://labuladong.gitee.io/algo/4/32/116/
这里要说明一点1并不是质数。
因为整数有一个性质,就是分解质因数的唯一性,及把一个大于1的整数分解质因数,他的形式是唯一的。而如果1是素数,则分解的形式就唯一的了,因为可以乘
若干个1。所以规定1不是素数。
class Solution {
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
Arrays.fill(isPrime, true);
for (int i = 2; i * i < n; i++)
if (isPrime[i]) {
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
int count = 0;
for (int i = 2; i < n; i++) {
if (isPrime[i]) {
count++;
}
}
return count;
}
}
292. Nim 游戏(巴什博弈)
你和你的朋友,两个人一起玩 Nim 游戏:
- 桌子上有一堆石头。
- 你们轮流进行自己的回合, 你作为先手 。
- 每一回合,轮到的人拿掉 1 - 3 块石头。
- 拿掉最后一块石头的人就是获胜者。
假设你们每一步都是最优解。请编写一个函数,来判断你是否可以在给定石头数量为 n 的情况下赢得游戏。如果可以赢,返回 true;否则,返回 false 。
参考题解:https://leetcode.cn/problems/nim-game/solution/gong-shui-san-xie-noxiang-xin-ke-xue-xi-wmz2t/
面对4的整数倍的人永远无法翻身,你拿N根对手就会拿4-N根,保证每回合共减4根,你永远面对4倍数,直到4. 相反,如果最开始不是4倍数,你可以拿掉刚好剩
下4倍数根,让他永远面对4倍数。
class Solution {
public boolean canWinNim(int n) {
return n % 4 != 0;
}
}
TopK
215. 数组中的第K个最大元素
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
题意分析:
题目要求我们找到「数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素」。「数组排序后的第 k 个最大的元素」换句话说:从右边往左边数第 k 个
元素(从 1 开始),那么从左向右数是第几个呢,我们列出几个找找规律就好了。
一共 6 个元素,找第 2 大,下标是 4;
一共 6 个元素,找第 4 大,下标是 2。
因此升序排序以后,目标元素的下标是 N−k,这里 N 是输入数组的长度。
第一种解法:快速排序,快速选择。
class Solution {
public int findKthLargest(int[] nums, int k) {
int len = nums.length;
// 第k大的元素在排序后数组中的位置
int target = len - k;
int left = 0;
int right = len - 1;
while (true) {
int pivotIndex = partition(nums, left, right);
// 根据每次得到的pivotIndex缩减区间
if (pivotIndex == target) {
return nums[pivotIndex];
} else if (pivotIndex < target) {
left = pivotIndex + 1;
} else if (pivotIndex > target) {
right = pivotIndex - 1;
}
}
}
// 采用双路快排
private int partition(int[] nums, int begin, int end) {
int random = (int) (Math.random() * (end - begin));
swap(nums, begin, begin + random);
int pivot = nums[begin];
while (begin < end) {
while (begin < end) {
if (nums[end] < pivot) {
nums[begin++] = nums[end];
break;
} else {
end--;
}
}
while (begin < end) {
if (nums[begin] > pivot) {
nums[end--] = nums[begin];
break;
} else {
begin++;
}
}
}
nums[begin] = pivot;
return begin;
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
第二种解法:堆排序
class Solution {
public int findKthLargest(int[] nums, int k) {
PriorityQueue<Integer> queue = new PriorityQueue<>();
for (int i = 0; i < k; i++) {
queue.offer(nums[i]);
}
for (int i = k; i < nums.length; i++) {
if (nums[i] > queue.peek()) {
queue.remove(queue.peek());
queue.offer(nums[i]);
}
}
return queue.peek();
}
}
第三种解法:自己建立堆
class Solution {
public int findKthLargest(int[] nums, int k) {
BinaryHeap heap = new BinaryHeap(k);
for (int i = 0; i < k; i++) {
heap.offer(nums[i]);
}
for (int i = k; i < nums.length; i++) {
if (nums[i] > heap.peek()) {
heap.remove(heap.peek());
heap.offer(nums[i]);
}
}
return heap.peek();
}
}
class BinaryHeap {
private int[] elements;
private int size;
private static final int DEFAULT_CAPACITY = 10;
public BinaryHeap(int[] elements, int k) {
if (elements == null || elements.length == 0) {
this.elements = new int[k];
} else {
size = elements.length;
int capacity = Math.max(DEFAULT_CAPACITY, size);
this.elements = new int[capacity];
for (int i = 0; i < elements.length; i++) {
this.elements[i] = elements[i];
}
}
heapify();
}
public BinaryHeap(int k) {
this(null, k);
}
private void heapify() {
for (int i = (size >> 1) - 1; i>= 0; i--) {
siftDown(i);
}
}
public int peek() {
return elements[0];
}
public void offer(int element) {
elements[size++] = element;
siftUp(size - 1);
}
public int remove(int element) {
int lastIndex = --size;
int delValue = elements[lastIndex];
elements[0] = elements[lastIndex];
elements[lastIndex] = 0;
siftDown(0);
return delValue;
}
private void siftUp(int index) {
int element = elements[index];
while (index > 0) {
int parentIndex = (index - 1) >> 1;
int parent = elements[parentIndex];
if (parent <= element) {
break;
}
elements[index] = parent;
index = parentIndex;
}
elements[index] = element;
}
private void siftDown(int index) {
int half = (size >> 1) - 1;
int element = elements[index];
while (index <= half) {
int childIndex = (index << 1) + 1;
int child = elements[childIndex];
int rightIndex = childIndex + 1;
if (rightIndex <= size - 1 && elements[rightIndex] < child) {
child = elements[childIndex = rightIndex];
}
if ((element <= child)) {
break;
}
// 来到这儿说明孩子节点更小
elements[index] = child;
index = childIndex;
}
elements[index] = element;
}
}
347. 前 K 个高频元素
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
class Solution {
public int[] topKFrequent(int[] nums, int k) {
int[] result = new int[k];
HashMap<Integer, Integer> map = new HashMap<>();
// 统计数组中每个数出现的频率
for (int num : nums) {
map.put(num, map.getOrDefault(num, 0) + 1);
}
Set<Map.Entry<Integer, Integer>> entries = map.entrySet();
// 根据map的value值正序排,相当于一个小顶堆
PriorityQueue<Map.Entry<Integer, Integer>> queue = new PriorityQueue<>((o1, o2) -> o1.getValue() - o2.getValue());
for (Map.Entry<Integer, Integer> entry : entries) {
queue.offer(entry);
if (queue.size() > k) {
// 移除堆顶元素
queue.poll();
}
}
for (int i = k - 1; i >= 0; i--) {
result[i] = queue.poll().getKey();
}
return result;
}
}
451. 根据字符出现频率排序
给定一个字符串 s ,根据字符出现的频率对其进行降序排序 。一个字符出现的频率是它出现在字符串中的次数。
返回 已排序的字符串 。如果有多个答案,返回其中任何一个。
// 哈希表
class Solution {
public String frequencySort(String s) {
Map<Character, Integer> count = new HashMap<>();
for(char c : s.toCharArray()){
count.put(c, count.getOrDefault(c, 0) + 1);
}
PriorityQueue<Map.Entry<Character, Integer>> items = new PriorityQueue<>((o1, o2) -> o2.getValue() - o1.getValue());
// 还有这种操作?
items.addAll(count.entrySet());
StringBuilder res = new StringBuilder();
// 当堆不为空时,一直让堆顶元素出堆。
while(!items.isEmpty()){
Map.Entry<Character, Integer> item = items.poll();
char key = item.getKey();
int val = item.getValue();
for(int i = 0; i < val; i++) {
res.append(key);
}
}
return res.toString();
}
}
692. 前K个高频单词
给定一个单词列表 words 和一个整数 k ,返回前 k 个出现次数最多的单词。
返回的答案应该按单词出现频率由高到低排序。如果不同的单词有相同出现频率, 按字典顺序排序。
class Solution {
public List<String> topKFrequent(String[] words, int k) {
// 1.先用哈希表统计单词出现的频率
Map<String, Integer> count = new HashMap();
for (String word : words) {
count.put(word, count.getOrDefault(word, 0) + 1);
}
// 2.构建小根堆 这里需要自己构建比较规则 此处为 lambda 写法 Java 的优先队列默认实现就是小根堆
PriorityQueue<String> minHeap = new PriorityQueue<>((s1, s2) -> {
// 当出现频率相同时,比较字典序。
if (count.get(s1).equals(count.get(s2))) {
// 若s2字典序在s1前面则s2.compareTo(s1) < 0
// 但是Comparator方法会认为s1字典序在s2前,实际上s1字典序在s2后面
// 因为Java的PriorityQueue默认是小顶堆,那么这时候会将代码认为的“小的”忘堆顶上滤
// 那么就会将实际字典序在后面的s1,往堆顶移动。
return s2.compareTo(s1);
} else {
return count.get(s1) - count.get(s2);
}
});
// 3.依次向堆加入元素。
for (String s : count.keySet()) {
minHeap.offer(s);
// 当堆中元素个数大于 k 个的时候,需要弹出堆顶最小的元素。
if (minHeap.size() > k) {
minHeap.poll();
}
}
// 4.依次弹出堆中的K个元素,放入结果集合中。
List<String> res = new ArrayList<>(k);
while (minHeap.size() > 0) {
res.add(minHeap.poll());
}
// 5.注意最后需要反转元素的顺序。
Collections.reverse(res);
return res;
}
}
多路归并
264. 丑数 II
给你一个整数 n ,请你找出并返回第 n 个 丑数 。
丑数 就是只包含质因数 2、3 、5 的正整数。
输入:n = 10
输出:12
解释:[1, 2, 3, 4, 5, 6, 8, 9, 10, 12] 是由前 10 个丑数组成的序列。
解法一:哈希表+优先级队列
class Solution {
public int nthUglyNumber(int n) {
HashSet<Long> set = new HashSet<>();
PriorityQueue<Long> queue = new PriorityQueue<>();
long ugly = 0;
int[] base = new int[] {2, 3, 5};
set.add(1l);
queue.offer(1l);
for (int i = 0; i < n; i++) {
ugly = queue.poll();
for (int b : base) {
long next = ugly * b;
// 如果为false那么说明set集合当中已经有了这个元素
if (set.add(next)) {
// 添加成功,接着加入到队列中
queue.offer(next);
}
}
}
return Math.toIntExact(ugly);
}
}
// TreeSet既有排序又有去重的功能。
class Solution {
public int nthUglyNumber(int n) {
TreeSet<Long> set = new TreeSet<>();
int[] baseUgly = new int[]{2, 3, 5};
set.add(1l);
for (int i = 1; i < n; i++) {
Long min = set.pollFirst();
for (int num : baseUgly) {
set.add(num * min);
}
}
return Math.toIntExact(set.pollFirst());
}
}
解法二:多路归并
对于一个丑数 n,均可以衍生出三个与之对应的丑数:n * 2, n * 3, n * 5
这个题目的有序链表需要通过求得的丑数来动态获取,所以我们利用三个指针 P2, P3, P5 分别指向正在被处理的丑数。
class Solution {
public int nthUglyNumber(int n) {
// 从下标 1 开始,放置丑数的数组。
int[] ans = new int[n + 1];
// 初始化,1默认是丑数。
ans[1] = 1;
// p2 p3 p5 分别表示 3 个质因数的指针
// idx 表示 ans 下一个存储的下标
for (int p2 = 1, p3 = 1, p5 = 1, idx = 2; idx <= n; idx++) {
// a b c 表示当前的三个元素,如上图橙色标识出的元素
int a = ans[p2] * 2, b = ans[p3] * 3, c = ans[p5] * 5;
// 求出三者的最小值
int min = Math.min(a, Math.min(b, c));
// 存储到 ans 中
ans[idx] = min;
// 指针后移 (同时具有去重的效果)
if (min == a) p2++;
if (min == b) p3++;
if (min == c) p5++;
}
// 返回第 n 个丑数
return ans[n];
}
}
313. 超级丑数
超级丑数是一个正整数,并满足其所有质因数都出现在质数数组 primes 中。
给你一个整数 n 和一个整数数组 primes ,返回第 n 个超级丑数 。
题目数据保证第 n 个超级丑数在 32-bit 带符号整数范围内。
输入:n = 12, primes = [2,7,13,19]
输出:32
解释:给定长度为 4 的质数数组 primes = [2,7,13,19],前 12 个超级丑数序列为:[1,2,4,7,8,13,14,16,19,26,28,32] 。
现在超级丑数的定义变为了一个数的全部质因数在给定的primes数组中那么这个数就是超级丑数。
我们仍然采用多路归并思想来做
class Solution {
public int nthSuperUglyNumber(int n, int[] primes) {
// 指针:每个质因数对应一个指针
int[] p = new int[primes.length];
// 存放丑数的数组
long[] ans = new long[n + 1];
ans[1] = 1;
// 初始化每个指针指向第一个丑数
Arrays.fill(p, 1);
for (int i = 2; i <= n; i++) {
// 求最小值
long min = Long.MAX_VALUE;
for (int j = 0; j < primes.length; j++) {
min = Math.min(min, ans[p[j]] * primes[j]);
}
// 指针后移 (同时具有去重的效果)
for (int j = 0; j < primes.length; j++) {
if (min == ans[p[j]] * primes[j]) {
p[j]++;
}
}
// 存储到 ans 中
ans[i] = min;
}
// 返回第 n 个丑数
return (int)ans[n];
}
}
单调栈
下一个更大的元素:
使用单调栈解决了「下一个更大元素」的问题,比如下面这个例子:
输入:nums = [1, 3, 2, 4, 4]
返回:res = [3, 4, 4, -1, -1]
我们实现了这样一个函数解决这个问题:
// 计算 nums 中每个元素的下一个更大元素
int[] nextGreaterElement(int[] nums) {
int n = nums.length;
// 存放答案的数组
int[] res = new int[n];
Stack<Integer> stack = new Stack<>();
// 因为是求 nums[i] 后面的元素,所以倒着往栈里放
for (int i = n - 1; i >= 0; i--) {
// 删掉 nums[i] 后面较小的元素,栈中只留下严格大于nums[i]的元素。
while (!stack.isEmpty() && stack.peek() <= nums[i]) {
stk.pop();
}
// 现在栈顶就是 nums[i] 身后的更大元素
res[i] = stack.isEmpty() ? -1 : stack.peek();
stack.push(nums[i]);
}
return res;
}
下一个更大或相等的元素:
本文给出这个问题的一些变体,比如说让你计算 nums[i] 的下一个大于等于 nums[i] 的元素怎么算?比如下面这个例子:
输入:nums = [1, 3, 2, 4, 4]
返回:res = [3, 4, 4, 4, -1]
其实很简单,把上面这段代码中 while 循环的 <= 号改成 < 号即可:
// 计算 nums 中每个元素的下一个更大或相等的元素
int[] nextGreaterOrEqualElement(int[] nums) {
int n = nums.length;
int[] res = new int[n];
Stack<Integer> stk = new Stack<>();
for (int i = n - 1; i >= 0; i--) {
// 把这里改成 < 号
while (!stk.isEmpty() && stk.peek() < nums[i]) {
stk.pop();
}
// 现在栈顶就是 nums[i] 身后的大于等于 nums[i] 的元素
res[i] = stk.isEmpty() ? -1 : stk.peek();
stk.push(nums[i]);
}
return res;
}
下一个更小的元素:
再变一变,如果让你计算 nums[i] 的下一个小于 nums[i] 的元素,怎么算?比如下面这个例子:
输入:nums = [8, 4, 6, 6, 3]
返回:res = [4, 3, 3, 3, -1]
也很简单,把之前实现的 nextGreaterElement 中 while 循环的 <= 条件改成 >= 条件即可得出下一个更小的元素:
// 计算 nums 中每个元素的下一个更小的元素
int[] nextLessElement(int[] nums) {
int n = nums.length;
// 存放答案的数组
int[] res = new int[n];
Stack<Integer> stk = new Stack<>();
// 倒着往栈里放
for (int i = n - 1; i >= 0; i--) {
// 删掉 nums[i] 后面较大的元素
while (!stk.isEmpty() && stk.peek() >= nums[i]) {
stk.pop();
}
// 现在栈顶就是 nums[i] 身后的更小元素
res[i] = stk.isEmpty() ? -1 : stk.peek();
stk.push(nums[i]);
}
return res;
}
下一个更小或相等的元素:
如果让你计算 nums[i] 的下一个小于或等于 nums[i] 的元素,怎么算?比如下面这个例子:
输入:nums = [8, 4, 6, 6, 3]
返回:res = [4, 3, 6, 3, -1]
类似的,把 nextLessElement 函数的 while 循环中的 >= 改成 > 即可:
// 计算 nums 中每个元素的下一个更小或相等的元素
int[] nextLessOrEqualElement(int[] nums) {
int n = nums.length;
// 存放答案的数组
int[] res = new int[n];
Stack<Integer> stk = new Stack<>();
// 倒着往栈里放
for (int i = n - 1; i >= 0; i--) {
// 删掉 nums[i] 后面较大的元素
while (!stk.isEmpty() && stk.peek() > nums[i]) {
stk.pop();
}
// 现在栈顶就是 nums[i] 身后的更小或相等元素
res[i] = stk.isEmpty() ? -1 : stk.peek();
stk.push(nums[i]);
}
return res;
}
上一个更大元素:
之前的 4 个例子都是计算 nums[i] 的下一个更大/更小元素,现在请你计算 nums[i] 的上一个更大元素,你会不会?比如这个例子:
输入:nums = [8, 7, 6, 7]
返回:res = [-1, 8, 7, 8]
注意之前我们的 for 循环都是从数组的尾部开始往栈里添加元素,这样栈顶元素就是 nums[i] 之后的元素。所以只要我们从数组的头部开始往栈里添加元素,栈
顶的元素就是 nums[i] 之前的元素,即可计算 nums[i] 的上一个更大元素。
代码实现如下:
// 计算 nums 中每个元素的上一个更大元素
int[] prevGreaterElement(int[] nums) {
int n = nums.length;
int[] res = new int[n];
Stack<Integer> stk = new Stack<>();
// 因为是求 nums[i] 前面的元素,所以正着往栈里放
for (int i = 0; i < n; i++) {
// 删掉 nums[i] 前面较小的元素
while (!stk.isEmpty() && stk.peek() <= nums[i]) {
stk.pop();
}
// 现在栈顶就是 nums[i] 前面的更大元素
res[i] = stk.isEmpty() ? -1 : stk.peek();
stk.push(nums[i]);
}
return res;
}
类似之前的几种实现,基于这个函数还可以求出 nums[i] 的上一个更大或相等的元素、上一个更小的元素、上一个更小或相等的元素,只要改一改 while 循环的
符号即可,下面一一列出具体实现。
上一个更大或相等的元素:
举例:
输入:nums = [8, 7, 6, 7]
返回:res = [-1, 8, 7, 8]
代码实现:
// 计算 nums 中每个元素的上一个更大或相等元素
int[] prevGreaterOrEqualElement(int[] nums) {
int n = nums.length;
int[] res = new int[n];
Stack<Integer> stk = new Stack<>();
for (int i = 0; i < n; i++) {
// 注意不等号
while (!stk.isEmpty() && stk.peek() < nums[i]) {
stk.pop();
}
// 现在栈顶就是 nums[i] 前面的更大或相等元素
res[i] = stk.isEmpty() ? -1 : stk.peek();
stk.push(nums[i]);
}
return res;
}
上一个更小的元素:
举例:
输入:nums = [3, 6, 6, 5]
返回:res = [-1, 3, 3, 3]
代码实现:
// 计算 nums 中每个元素的上一个更小的元素
int[] prevLessElement(int[] nums) {
int n = nums.length;
int[] res = new int[n];
Stack<Integer> stk = new Stack<>();
for (int i = 0; i < n; i++) {
// 把 nums[i] 之前的较大元素删除
while (!stk.isEmpty() && stk.peek() >= nums[i]) {
stk.pop();
}
// 现在栈顶就是 nums[i] 前面的更小元素
res[i] = stk.isEmpty() ? -1 : stk.peek();
stk.push(nums[i]);
}
return res;
}
上一个更小或相等的元素:
举例:
输入:nums = [3, 6, 6, 5]
返回:res = [-1, 3, 6, 3]
代码实现:
// 计算 nums 中每个元素的上一个更小或相等元素
int[] prevLessOrEqualElement(int[] nums) {
int n = nums.length;
int[] res = new int[n];
Stack<Integer> stk = new Stack<>();
for (int i = 0; i < n; i++) {
// 注意不等号
while (!stk.isEmpty() && stk.peek() > nums[i]) {
stk.pop();
}
// 现在栈顶就是 nums[i] 前面的更小或相等元素
res[i] = stk.isEmpty() ? -1 : stk.peek();
stk.push(nums[i]);
}
return res;
}
496. 下一个更大元素 I
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。
给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ,找出满足 nums1[i] == nums2[j] 的下标 j ,并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更
大元素,那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案,满足 ans[i] 是如上所述的 下一个更大元素 。
输入:nums1 = [4,1,2], nums2 = [1,3,4,2].
输出:[-1,3,-1]
解释:nums1 中每个值的下一个更大元素如下所述:
- 4 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
- 1 ,用加粗斜体标识,nums2 = [1,3,4,2]。下一个更大元素是 3 。
- 2 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
参考题解:https://labuladong.gitee.io/algo/2/23/63/
class Solution {
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
int[] result = new int[nums1.length];
int[] grater = nextGraterElement(nums2);
HashMap<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums2.length; i++) {
map.put(nums2[i], grater[i]);
}
for (int i = 0; i < nums1.length; i++) {
result[i] = map.get(nums1[i]);
}
return result;
}
private int[] nextGraterElement(int[] nums) {
int n = nums.length;
Stack<Integer> stack = new Stack<>();
int[] res = new int[n];
for (int i = n - 1; i >= 0; i--) {
while (!stack.isEmpty() && nums[i] > stack.peek()) {
stack.pop();
}
res[i] = stack.isEmpty() ? -1 : stack.peek();
stack.push(nums[i]);
}
return res;
}
}
503. 下一个更大元素 II⭐⭐⭐(环状数组)
给定一个循环数组 nums ( nums[nums.length - 1] 的下一个元素是 nums[0] ),返回 nums 中每个元素的 下一个更大元素 。
数字 x 的 下一个更大的元素 是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。
如果不存在,则输出 -1 。
这个问题肯定还是要用单调栈的解题模板,但难点在于,比如输入是 [2,1,2,4,3],对于最后一个元素 3,如何找到元素 4 作为下一个更大元素。
对于这种需求,常用套路就是将数组长度翻倍:
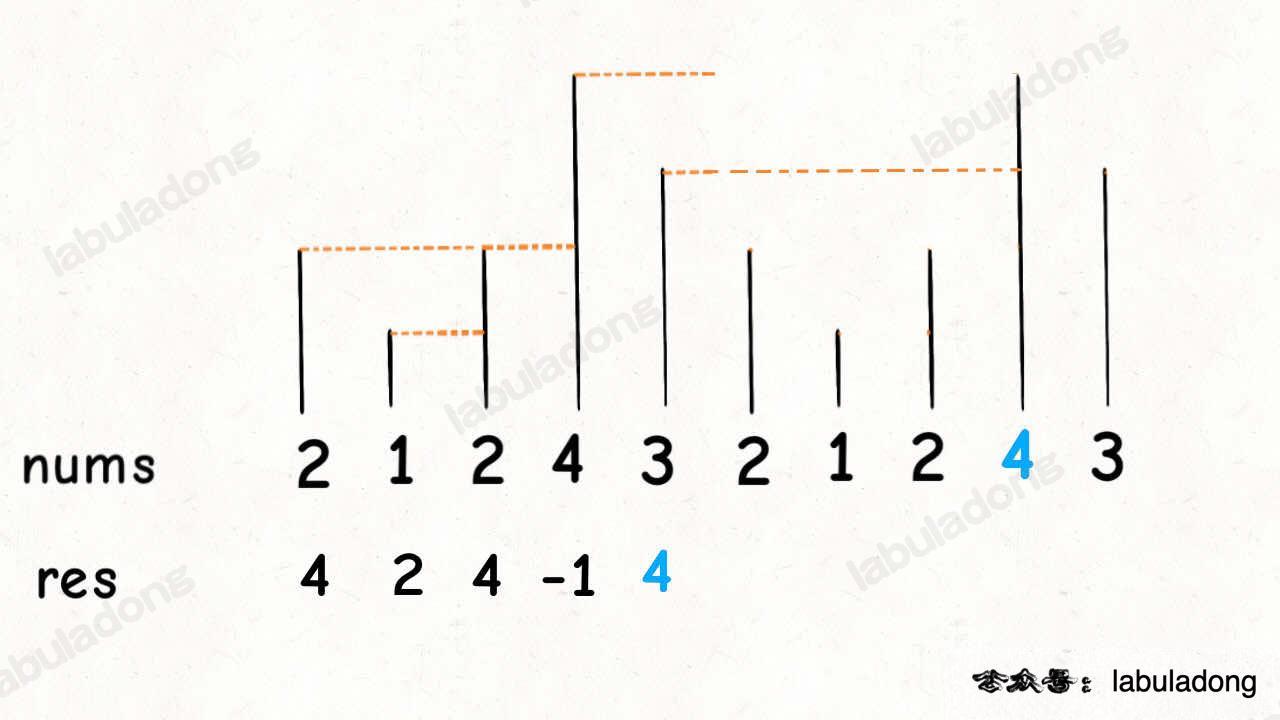
class Solution {
public int[] nextGreaterElements(int[] nums) {
int len = nums.length;
int[] res = new int[len];
Stack<Integer> stack = new Stack<>();
for (int i = 2 * len - 1; i >= 0; i--) {
while (!stack.isEmpty() && nums[i % len] >= stack.peek()) {
stack.pop();
}
res[i % len] = stack.isEmpty() ? -1 : stack.peek();
stack.push(nums[i % len]);
}
return res;
}
}
739. 每日温度⭐
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在
这之后都不会升高,请在该位置用 0 来代替。
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
int len = temperatures.length;
int[] res = new int[len];
Stack<Integer> stack = new Stack<>();
// 我们的单调栈模板是倒着遍历的
for (int i = len - 1; i >= 0; i--) {
// 这里要注意小于等于我们都要将栈顶元素弹出,因为温度数组种有相同的温度,我们是要找到更高的温度是在几天后。
// 两个索引位置相差几天就是将索引位置相减。
while (!stack.isEmpty() && temperatures[stack.peek()] <= temperatures[i]) {
stack.pop();
}
res[i] = stack.isEmpty() ? 0 : stack.peek() - i;
stack.push(i);
}
return res;
}
}
901. 股票价格跨度
class StockSpanner {
Stack<int[]> stack = new Stack<>();
public int next(int price) {
int count = 1;
while (!stack.isEmpty() && stack.peek()[0] <= price) {
int[] prev = stack.pop();
count += prev[1];
}
stack.push(new int[]{price, count});
return count;
}
}
402. 移掉 K 位数字⭐
给你一个以字符串表示的非负整数 num 和一个整数 k ,移除这个数中的 k 位数字,使得剩下的数字最小。请你以字符串形式返回这个最小的数字。
输入:num = "1432219", k = 3
输出:"1219"
解释:移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219 。
如果想让结果尽可能小,那么清除数字分两步:
1、先删除 num 中的若干数字,使得 num 从左到右每一位都单调递增。比如 14329 转化成 129,这需要使用到 单调栈技巧;
2、num 中的每一位变成单调递增的之后,如果 k 还大于 0(还可以继续删除)的话,则删除尾部的数字,比如 129 删除成 12。
删掉一些数使 num 从左到右每一位都单调递增会比删低位的数缩减更大。
class Solution {
public String removeKdigits(String num, int k) {
Stack<Character> stk = new Stack<>();
for (char c : num.toCharArray()) {
// 单调栈代码模板 单调增(从栈底到栈顶方向)
// 准备添加的数小于栈顶元素时,移除栈顶元素。
while (!stk.isEmpty() && c < stk.peek() && k > 0) {
stk.pop();
k--;
}
// 防止 0 作为数字的开头
// 栈为空时,还将0放入栈,最终结果就是以 0 作为数字开头。
if (stk.isEmpty() && c == '0') {
continue;
}
stk.push(c);
}
// 此时栈中元素单调递增,若 k 还没用完的话删掉栈顶元素
while (k > 0 && !stk.isEmpty()) {
stk.pop();
k--;
}
// 若最后没剩下数字,就是 0
if (stk.isEmpty()) {
return "0";
}
// 将栈中字符转化成字符串
StringBuilder sb = new StringBuilder();
while (!stk.isEmpty()) {
sb.append(stk.pop());
}
// 出栈顺序和字符串顺序是反的
return sb.reverse().toString();
}
}
1019. 链表中的下一个更大节点
给定一个长度为 n 的链表 head
对于列表中的每个节点,查找下一个 更大节点 的值。也就是说,对于每个节点,找到它旁边的第一个节点的值,这个节点的值 严格大于 它的值。
返回一个整数数组 answer ,其中 answer[i] 是第 i 个节点( 从1开始 )的下一个更大的节点的值。如果第 i 个节点没有下一个更大的节点,设置 answer[i] = 0 。
class Solution {
public int[] nextLargerNodes(ListNode head) {
Stack<Integer> stack = new Stack<>();
ArrayList<Integer> list = new ArrayList();
while (head != null) {
list.add(head.val);
head = head.next;
}
int[] res = new int[list.size()];
for (int i = list.size() - 1; i >= 0; i--) {
while (!stack.isEmpty() && stack.peek() <= list.get(i)) {
stack.pop();
}
res[i] = stack.isEmpty() ? 0 : stack.peek();
stack.push(list.get(i));
}
return res;
}
}
1475. 商品折扣后的最终价格
给你一个数组 prices ,其中 prices[i] 是商店里第 i 件商品的价格。
商店里正在进行促销活动,如果你要买第 i 件商品,那么你可以得到与 prices[j] 相等的折扣。
其中 j 是满足 j > i 且 prices[j] <= prices[i] 的 最小下标 ,如果没有满足条件的 j ,你将没有任何折扣。
请你返回一个数组,数组中第 i 个元素是折扣后你购买商品 i 最终需要支付的价格。
class Solution {
public int[] finalPrices(int[] prices) {
int len = prices.length;
Stack<Integer> stack = new Stack<>();
int[] discount = new int[len];
int[] res = new int[len];
for (int i = len - 1; i >= 0; i--) {
while (!stack.isEmpty() && stack.peek() > prices[i]) {
stack.pop();
}
discount[i] = stack.isEmpty() ? 0 : stack.peek();
stack.push(prices[i]);
}
for (int i = 0; i < len; i++) {
res[i] = prices[i] - discount[i];
}
return res;
}
}
1944. 队列中可以看到的人数⭐⭐
有 n 个人排成一个队列,从左到右 编号为 0 到 n - 1 。给你以一个整数数组 heights ,每个整数 互不相同,heights[i] 表示第 i 个人的高度。
一个人能 看到 他右边另一个人的条件是这两人之间的所有人都比他们两人 矮 。
更正式的,第 i 个人能看到第 j 个人的条件是 i < j 且 min(heights[i], heights[j]) > max(heights[i+1], heights[i+2], ..., heights[j-1]) 。
请你返回一个长度为 n 的数组 answer ,其中 answer[i] 是第 i 个人在他右侧队列中能 看到 的 人数 。
提示:
- n == heights.length
- 1 <= n <= 105
- 1 <= heights[i] <= 105
- heights 中所有数 互不相同 。
class Solution {
public int[] canSeePersonsCount(int[] heights) {
int len = heights.length;
Stack<Integer> stack = new Stack<>();
int[] res = new int[len];
for (int i = len - 1; i >= 0; i--) {
int count = 0;
// 让栈中存放严格大于heights[i]的元素
while (!stack.isEmpty() && stack.peek() <= heights[i]) {
stack.pop();
// 每从栈中拿出一个小于等于heights[i]的数,count + 1。
count++;
}
// 当栈不为空时还能看到栈顶元素,所以 count + 1。
res[i] = stack.isEmpty() ? count : count + 1;
stack.push(heights[i]);
}
return res;
}
}
907. 子数组的最小值之和⭐⭐⭐⭐
给定一个整数数组 arr,找到 min(b) 的总和,其中 b 的范围为 arr 的每个(连续)子数组。
由于答案可能很大,因此返回答案模 10^9 + 7。
输入:arr = [3,1,2,4]
输出:17
解释:
子数组为 [3],[1],[2],[4],[3,1],[1,2],[2,4],[3,1,2],[1,2,4],[3,1,2,4]。
最小值为 3,1,2,4,1,1,2,1,1,1,和为 17。
题目的原问题:求每个子数组中最小值之和
我们不妨可以把问题稍微转换一下,如果我们知道以某一个元素为最小值的所有子数组数量,那么该元素的贡献值就是val * n
现在我们需要解决的是怎么得到某一个元素的覆盖范围呢??
- 向左寻找第一个小于等于该元素的第一个元素,下标记为left
- 向右寻找第一个小于该元素的第一个元素,下标记为right
注意:
- 我们得到的区间为(left, right),均为开区间,也就是说下标left和right是取不到滴;
- 向左向右寻找一定需要有一边是到等于就停止,否则如果存在相同元素,会出现子数组重复的问题。
做好了上述准备数据后,我们如何求满足数量呢??
很简单,分别求出「以i结尾的子数组数量」和「以i开头的子数组数量」
即:num = (i - left) * (right - i)
因为(left, right)是开区间,所以不需要+1
最终代码如下:
class Solution {
public int sumSubarrayMins(int[] arr) {
int MOD = (int) 1e9 + 7;
int n = arr.length;
int[] left = new int[n];
int[] right = new int[n];
// 用stackNext栈来存放下一个小于当前元素的第一个元素的下标。
Stack<Integer> stackNext = new Stack<>();
// 用stackPrev栈来存放前一个小于等于当前元素的第一个元素的下标。
Stack<Integer> stackPrev = new Stack<>();
for (int i = n - 1; i >= 0; i--) {
while (!stackNext.isEmpty() && arr[stackNext.peek()] >= arr[i]) {
stackNext.pop();
}
// 注意这里如果栈为空时,说明后面没有比当前元素小的元素,记录下标为数组长度n。
right[i] = stackNext.isEmpty() ? n : stackNext.peek();
stackNext.push(i);
}
for (int i = 0; i < n; i++) {
while (!stackPrev.isEmpty() && arr[stackPrev.peek()] > arr[i]) {
stackPrev.pop();
}
// 注意这里如果栈为空时,说明前面没有比当前元素小的元素,记录下标为-1。i - (-1)就会得到正确的长度
// 这些地方都是小细节。
left[i] = stackPrev.isEmpty() ? -1 : stackPrev.peek();
stackPrev.push(i);
}
long ans = 0;
for (int i = 0; i < n; i++) {
ans = (ans + (long)(i - left[i]) * (right[i] - i) * arr[i]) % MOD;
}
return (int) ans;
}
}
2104. 子数组范围和⭐⭐⭐⭐
给你一个整数数组 nums 。nums 中,子数组的 范围 是子数组中最大元素和最小元素的差值。
返回 nums 中 所有 子数组范围的 和 。
子数组是数组中一个连续 非空 的元素序列。
数组
4. 寻找两个正序数组的中位数⭐
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
第一种解法时间复杂度不满足要求
/**
* 暴力解法
*/
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
// 合并两个有序数组
int[] arr = mergeArray(nums1, nums2);
int n = arr.length;
if (n % 2 == 0) {
return (arr[(n - 1) / 2] + arr[n / 2]) / 2.0;
} else {
return arr[n / 2];
}
}
private int[] mergeArray(int[] nums1, int[] nums2) {
int m = nums1.length;
int n = nums2.length;
// 将两个数组中的元素合并到一个新的数组arr中
int[] arr = new int[m + n];
int i = 0, j = 0, k = 0;
// 直到把某一个数组合并完退出循环
while (i < m && j < n) {
arr[k++] = nums1[i] < nums2[j] ? nums1[i++] : nums2[j++];
}
// 下面两个while循环判断是哪个数组没处理完,继续处理。
while (i < m) {
arr[k++] = nums1[i++];
}
while (j < n) {
arr[k++] = nums2[j++];
}
return arr;
}
}
31. 下一个排列
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
- 例如,arr = [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个
排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
- 例如,arr = [1,2,3] 的下一个排列是 [1,3,2] ;
- 类似地,arr = [2,3,1] 的下一个排列是 [3,1,2];
- 而 arr = [3,2,1] 的下一个排列是 [1,2,3] ,因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组 nums ,找出 nums 的下一个排列。
必须 原地 修改,只允许使用额外常数空间。
参考题解:https://leetcode.cn/problems/next-greater-element-iii/solution/by-lfool-vi69/
class Solution {
public void nextPermutation(int[] nums) {
int n = nums.length;
for (int i = n - 1; i >= 0; i--) {
// 从后往前找到第一对连续的升序的两个数。
if (nums[i] > nums[i - 1]) {
// 对i - 1索引位置后面的元素进行排序。
Arrays.sort(nums, i, n);
for (int j = i; j < n; j++) {
if (nums[j] > nums[i - 1]) {
int temp = nums[i - 1];
nums[i - 1] = nums[j];
nums[j] = temp;
// 一定要及时return。
return;
}
}
}
}
Arrays.sort(nums);
}
}
41. 缺失的第一个正数(原地哈希)⭐⭐⭐😜
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
输入:nums = [3,4,-1,1]
输出:2
解题思路:
数组长度为n,那么可能出现的最大正数就是n,比如数组长度为5,数组中的元素为1 2 3 4 5。
那数组中没有出现的最小正整数就会在[1, n + 1]之间。n + 1是因为数组中的元素是从1自增到n。那么没出现的最小正整数就是n + 1。
那么我们把1放在下标为0的位置上,把2放在下标为1的位置上......按照这种思路整理一遍数组。然后我们再遍历一次数组,第 1个遇到的它的值不等于下标的那个
数,就是我们要找的缺失的第一个正数。
这个思想就相当于我们自己编写哈希函数,这个哈希函数的规则特别简单,那就是数值为 i 的数映射到下标为 i - 1 的位置。
class Solution {
public int firstMissingPositive(int[] nums) {
int len = nums.length;
for (int i = 0; i < len; i++) {
// 因为正数的范围是在 1 - n 之间的,如果不在这个范围的数,不用进行交换,不做处理。
// nums[nums[i] - 1] == nums[i] 表示nums[i]在对应的索引位置上,就不用交换。
while (nums[i] > 0 && nums[i] <= len && nums[nums[i] - 1] != nums[i]) {
// 满足在指定范围内、并且没有放在正确的位置上,才交换
// 例如:数值 3 应该放在索引 2 的位置上
swap(nums, nums[i] - 1, i);
}
}
// [1, -1, 3, 4]
for (int i = 0; i < len; i++) {
if (nums[i] - 1 != i) {
return i + 1;
}
}
// 都正确则返回数组长度 + 1
return len + 1;
}
private void swap(int[] nums, int index1, int index2) {
int temp = nums[index1];
nums[index1] = nums[index2];
nums[index2] = temp;
}
}
442. 数组中重复的数据(原地哈希)⭐⭐😜
给你一个长度为 n 的整数数组 nums ,其中 nums 的所有整数都在范围 [1, n] 内,且每个整数出现 一次 或 两次 。
请你找出所有出现 两次 的整数,并以数组形式返回。
你必须设计并实现一个时间复杂度为 O(n) 且仅使用常量额外空间的算法解决此问题。
class Solution {
public List<Integer> findDuplicates(int[] nums) {
List<Integer> res = new ArrayList<>();
int n = nums.length;
for (int i = 0; i < n; i++) {
int index = Math.abs(nums[i]) - 1;
if (nums[index] < 0) {
res.add(Math.abs(nums[i]));
} else {
nums[index] *= -1;
}
}
return res;
}
}
448. 找到所有数组中消失的数字(原地哈希)⭐⭐😜
给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。
解题思路:
class Solution {
public List<Integer> findDisappearedNumbers(int[] nums) {
// 用来存放结果
List<Integer> res = new ArrayList<>();
// 1. 遍历下数组的元素,对对应的索引位置的元素作标记
int len = nums.length;
for(int i = 0; i < len; i++) {
int num = Math.abs(nums[i]); // 由于数组的元素有可能被*-1,所以取绝对值
int index = num - 1;
if (nums[index] > 0) {
nums[index] *= -1;
}
}
// 寻找没有标记的索引位置
for (int i = 0; i < len; i++) {
if (nums[i] > 0) {
int num = i + 1; // 将索引转化为对应的元素
res.add(num);
}
}
return res;
}
}
645. 错误的集合(原地哈希)⭐⭐😜
集合 s 包含从 1 到 n 的整数。不幸的是,因为数据错误,导致集合里面某一个数字复制了成了集合里面的另外一个数字的值.
导致集合 丢失了一个数字 并且 有一个数字重复 。
给定一个数组 nums 代表了集合 S 发生错误后的结果。
请你找出重复出现的整数,再找到丢失的整数,将它们以数组的形式返回。
解题思路:
class Solution {
public int[] findErrorNums(int[] nums) {
int n = nums.length;
int dup = -1;
for (int i = 0; i < n; i++) {
// 得到nums[i]应该存放的索引位置
// 我们让nums[i]放到nums[i] - 1这个索引位置。
// 很可能nums[i]这个数已经被标记了所以要加绝对值。
int index = Math.abs(nums[i]) - 1;
// 发现该位置已经被标记,此时i位置原来的数就是重复的。
if (nums[index] < 0) {
dup = Math.abs(nums[i]);
} else {
// 该位置还没有被标记,乘以-1。
// nums[i]被置为负数,说明i + 1存在于数组中。
nums[index] *= -1;
}
}
int missing = -1;
for (int i = 0; i < n; i++) {
// 若某个位置没有被标记,那i + 1就是缺少的数。
if (nums[i] > 0) {
missing = i + 1;
}
}
return new int[]{dup, missing};
}
}
287. 寻找重复数⭐⭐⭐⭐
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。
你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。
解题思路:前面的四道题重复的数只出现一次,并不会出现多次。这道题也可以用原地哈希的办法,但是这样就修改了原始的数组。
https://leetcode.cn/problems/find-the-duplicate-number/solution/by-longluo-e315/
class Solution {
public int findDuplicate(int[] nums) {
int n = nums.length;
for (int i = 0; i < n; i++) {
int index = Math.abs(nums[i]) - 1;
if (nums[index] < 0) {
return Math.abs(nums[i]);
} else {
nums[index] *= -1;
}
}
return -1;
}
}
不修改原始数组
26. 删除有序数组中的重复项
给你一个 升序排列 的数组 nums ,请你原地删除重复出现的元素,使每个元素只出现一次 ,返回删除后数组的新长度。元素的相对顺序应该保持一致 。
由于在某些语言中不能改变数组的长度,所以必须将结果放在数组nums的第一部分。更规范地说,如果在删除重复项之后有 k 个元素,那么 nums 的前 k 个元素
应该保存最终结果。
题目:外面有宝,赶紧捡回来按序放好,不能重样哟 有点像小夫妻俩,老公q在外面淘宝,找到后运回来,找到一个新的宝,老婆p在家里就给挖个新坑放好,最
后外面没宝了,就结束咯。
中间对话
老公:老婆,这个家里有没?(if) 老婆:有了。(nums[p] == nums[q])你再找找(q++)
老公:老婆,这个家里有没?(if) 老婆:有了。(nums[p] == nums[q])你再找找(q++)
老公:老婆,这个家里有没?(if) 老婆:这个没有,拿回来吧 (nums[p] != nums[q]) 放好了,我到下一个位置等你(p++) 你再继续找吧(q++)
class Solution {
public int removeDuplicates(int[] nums) {
int left = 0, right = 0;
// 当right移动到nums.length - 1之后结束循环
while (right < nums.length) {
if (nums[right] != nums[left]) {
// 先让left++,再覆盖。
left++;
nums[left] = nums[right];
}
right++;
}
return left + 1;
}
}
// 通解写法
class Solution {
public int removeDuplicates(int[] nums) {
return process(nums, 1);
}
public int process(int[] nums, int k ) {
int left = 0;
for (int right = 0; right < nums.length; right++) {
if (left < k || nums[left - k] != nums[right]) {
nums[left++] = nums[right];
}
}
return left;
}
}
关键点就是只有nums[i] != nums[j]才移动j,然后用nums[i]覆盖nums[j]。
80. 删除有序数组中的重复项 II⭐
给你一个有序数组 nums ,请你原地删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。
不要使用额外的数组空间,你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。
解题思路:
为了让解法更具有一般性,我们将原问题的「保留 2 位」修改为「保留 k 位」。
对于此类问题,我们应该进行如下考虑:
- 由于是保留 k 个相同数字,对于前 k 个数字,我们可以直接保留;
- 对于后面的任意数字,能够保留的前提是:与当前写入的位置前面的第 k 个元素进行比较,不相同则保留。
class Solution {
public int removeDuplicates(int[] nums) {
return process(nums, 2);
}
public int process(int[] nums, int k ) {
int left = 0;
for (int right = 0; right < nums.length; right++) {
if (left < k || nums[left - k] != nums[right]) {
nums[left++] = nums[right];
}
}
return left;
}
}
27. 移除元素⭐
给你一个数组 nums 和一个值 val,你需要原地移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
class Solution {
public int removeElement(int[] nums, int val) {
int j = nums.length - 1;
for (int i = 0; i <= j; i++) {
// 当nums[i] != val时,只移动i
if (nums[i] == val) {
// 这里一定要让i--,因为交换回来的数也可能等于val,同样需要处理,如果直接不i--直接i,那么循环结束时i++。
// 交换回来的数就没有处理到。先i--,再i++。
swap(nums, i--, j--);
}
}
// 当 j < i时说明所有val值已经移除。
return j + 1;
}
public void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
// 双指针解法
class Solution {
public int removeElement(int[] nums, int val) {
int fast = 0, slow = 0;
while (fast < nums.length) {
if (nums[fast] != val) {
nums[slow] = nums[fast];
slow++;
}
fast++;
}
return slow;
}
}
56. 合并区间⭐⭐🌷
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回一个不重叠的区间数组,该数组需恰好
覆盖输入中的所有区间 。
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
1.将所有的区间按照左端点从小到大排序

2.定义区间左端点l = a[0] [0] ,右端点 r = a[0] [1](等价于两个左右指针),我们从前往后遍历每个区间:
如果当前区间和上一个区间没有交集,也就是说当前区间的左端点>上一个区间的右端点,即a[i] [0] > r,说明上一个区间独立,我们将上一个区间的左右端点[l,r]
加入答案数组中,并更新左端点l,右端点r为当前区间的左右端点,即l = a[i] [0], r = a[i] [1]。
关键点:始终维持l和r为最新独立区间的左右端点。
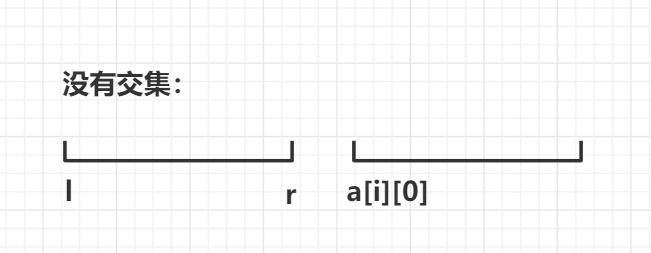
如果当前区间和上一个区间有交集,即当前区间的左端点<=上一个区间的右端点,我们让左端点l保持不变,右端点r更新为max(r, a[i] [1]) ,进行区间的合并 。
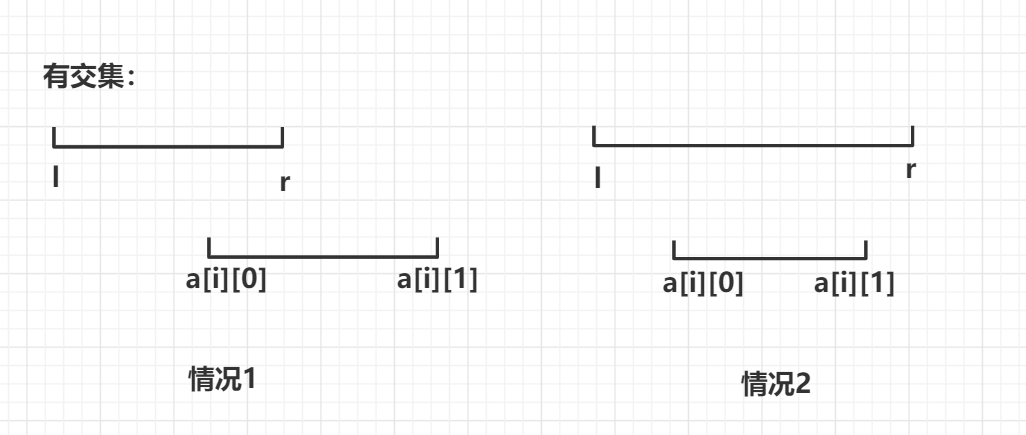
3.最后再将最后一个合并或者未合并的独立区间[l,r]加入答案数组中。
class Solution {
public int[][] merge(int[][] a) {
List<int[]> res = new ArrayList<>();
// 按照每个区间的左端点进行排序
Arrays.sort(a, (x, y) -> x[0] - y[0]);
int l = a[0][0], r = a[0][1];
for (int i = 1; i < a.length; i++) {
// 当前区间的左端点比上一区间的右端点大,将上一区间加入结果集。
if (a[i][0] > r) {
res.add(new int[]{l, r});
l = a[i][0];
r = a[i][1];
} else {
// 来到这个分支说明,当前区间的左端点小于等于上一区间的右端点。有可能是区间相交,有可能是覆盖区间。
// 因为之前已经按照左端点排好序了。
// 这里只需要确定右端点就行了。
r = Math.max(r, a[i][1]);
}
}
res.add(new int[]{l, r});
// 在将数组作为参数传递给toArray方法时,不需要为数组提供精确的大小。
return res.toArray(new int[0][0]);
}
}
57. 插入区间⭐⭐🌷
给你一个 无重叠的 ,按照区间起始端点排序的区间列表。
在列表中插入一个新的区间,你需要确保列表中的区间仍然有序且不重叠(如果有必要的话,可以合并区间)。
输入:intervals = [[1,3],[6,9]], newInterval = [2,5]
输出:[[1,5],[6,9]]
class Solution {
public int[][] insert(int[][] intervals, int[] newInterval) {
int length = intervals.length;
int[][] newIntervals = new int[length + 1][2];
for (int i = 0; i < intervals.length; i++) {
newIntervals[i] = intervals[i];
}
newIntervals[length] = newInterval;
Arrays.sort(newIntervals, (x, y) -> x[0] - y[0]);
List<int[]> res = new ArrayList<>();
int l = newIntervals[0][0];
int r = newIntervals[0][1];
for (int i = 1; i < newIntervals.length; i++) {
if (newIntervals[i][0] > r) {
res.add(new int[]{l, r});
l = newIntervals[i][0];
r = newIntervals[i][1];
} else {
r = Math.max(r, newIntervals[i][1]);
}
}
res.add(new int[]{l, r});
return res.toArray(new int[0][]);
}
}
1288. 删除被覆盖区间⭐⭐🌷
给你一个区间列表,请你删除列表中被其他区间所覆盖的区间。
只有当 c <= a 且 b <= d 时,我们才认为区间 [a,b) 被区间 [c,d) 覆盖。
在完成所有删除操作后,请你返回列表中剩余区间的数目。
解题思路:
题目问我们,去除被覆盖区间之后,还剩下多少区间,那么我们可以先算一算,被覆盖区间有多少个,然后和总数相减就是剩余区间数。
对于这种区间问题,如果没啥头绪,首先排个序看看,比如我们按照区间的起点进行升序排序:
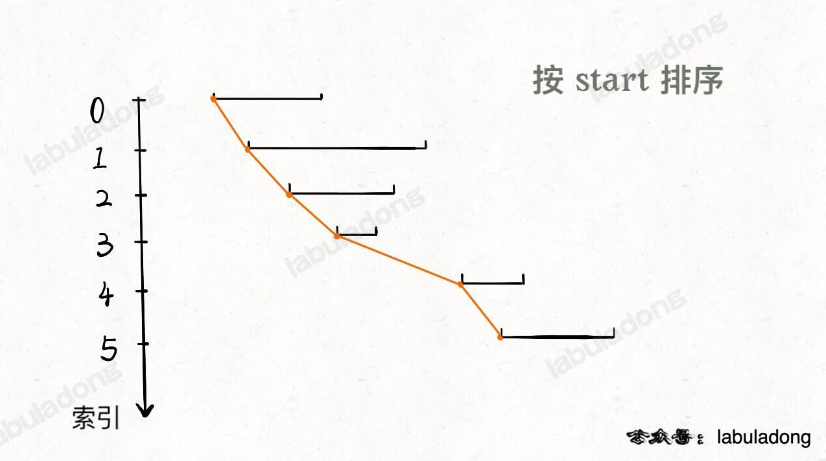
排序之后,两个相邻区间可能有如下三种相对位置:
对于这三种情况,我们应该这样处理:
对于情况一,找到了覆盖区间。
对于情况二,两个区间可以合并,成一个大区间。
对于情况三,两个区间完全不相交。
依据几种情况,我们可以写出如下代码:
class Solution {
public int removeCoveredIntervals(int[][] intervals) {
// 区间起点相同时,按照区间终点降序排序。
Arrays.sort(intervals, (a, b) -> {
if (a[0] == b[0]) {
return b[1] - a[1];
} else {
return a[0] - b[0];
}
});
// res记录被覆盖区间数目。
int res = 0;
int left = intervals[0][0];
int right = intervals[0][1];
for (int i = 1; i < intervals.length; i++) {
// 情况一,找到覆盖区间
if (left <= intervals[i][0] && right >= intervals[i][1]) {
res++;
}
// 情况二,更新left和right
if (right >= intervals[i][0] && right <= intervals[i][1]) {
left = intervals[i][0];
right = intervals[i][1];
}
// 情况三,完全不相交,更新起点和终点
if (right < intervals[i][0]) {
left = intervals[i][0];
right = intervals[i][1];
}
}
return intervals.length - res;
}
}
以上就是本题的解法代码,起点升序排列,终点降序排列的目的是防止如下情况:
对于这两个起点相同的区间,我们需要保证长的那个区间在上面(按照终点降序),这样才会被判定为覆盖,否则会被错误地判定为相交,少算一个覆盖区间。
986. 区间列表的交集⭐⭐⭐🌷
给定两个由一些 闭区间 组成的列表,firstList 和 secondList ,其中 firstList[i] = [starti, endi] 而 secondList[j] = [startj, endj] 。
每个区间列表都是成对 不相交 的,并且 已经排序 。
返回这 两个区间列表的交集 。
形式上,闭区间 [a, b](其中 a <= b)表示实数 x 的集合,而 a <= x <= b 。
两个闭区间的 交集 是一组实数,要么为空集,要么为闭区间。例如,[1, 3] 和 [2, 4] 的交集为 [2, 3] 。
参考题解:https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_6298794fe4b01a4852072f9b/1
class Solution {
public int[][] intervalIntersection(int[][] firstList, int[][] secondList) {
List<int[]> res = new ArrayList<>();
int i = 0, j = 0;
while (i < firstList.length && j < secondList.length) {
int a1 = firstList[i][0], a2 = firstList[i][1];
int b1 = secondList[j][0], b2 = secondList[j][1];
if (b2 >= a1 && a2 >= b1) {
res.add(new int[]{Math.max(a1, b1), Math.min(a2, b2)});
}
if (a2 > b2) {
j++;
} else {
i++;
}
}
return res.toArray(new int[0][]);
}
}
66. 加一
给定一个由整数组成的非空数组所表示的非负整数,在该数的基础上加一。
最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。
你可以假设除了整数 0 之外,这个整数不会以零开头。
输入:digits = [1,2,3]
输出:[1,2,4]
解释:输入数组表示数字 123。
class Solution {
// 从后向前遍历,不为9时:直接加一,为9时让当前元素重置为0
public int[] plusOne(int[] digits) {
for (int i = digits.length - 1; i >= 0; i--) {
// 如果等于 9 ,重置为0
if (digits[i] == 9) {
digits[i] = 0;
} else {
// 不为9,直接加一返回
digits[i]++;
return digits;
}
}
// 循环出来:如果没返回则:所有的位都已经重置为 0了 ,只需要数组扩容1在前面加一即可
//如果所有位都是进位,则长度+1
digits = new int[digits.length + 1];
digits[0] = 1;
return digits;
}
}
75. 颜色分类⭐
给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库的sort函数的情况下解决这个问题。
输入:nums = [2,0,2,1,1,0]
输出:[0,0,1,1,2,2]
题目最后给出的「进阶」要求,其实考察的是「快速排序」的子过程 partition,即:通过一次遍历,把数组分成三个部分。
写代码的时候需要注意到设置的变量以及区间的定义,也就是 循环不变量。循环不变量 简单说就是在循环的过程中保持不变的性质,这个性质是人为根据需要解
决的任务定义的。
对 循环不变量 的简单认识:
- 变量的值是变化的,但是保持不变的性质,就是循环不变量;
- 这里的「量」是一些人为定义的、可以判断真假的语句,在循环开始前、循环的过程中、循环结束以后,都为真;
- 这里的「循环」是广义上的,并不一定指「循环」,也有可能是在「递归」的过程中。
class Solution {
public void sortColors(int[] nums) {
int len = nums.length;
if (len < 2) {
return;
}
// 我们用zero和two两个指针将数组分为3个区间
// all num in [0, zero) = 0
// all num in [zero, i) = 1
// all num in (two, len - 1] = 2
int zero = 0; // 当zero初始化为0时 [0, zero)是空区间
int two = len - 1; // 当two初始化为len - 1时 (two, len - 1]是空区间
int i = 0;
// 当i == two时第二个区间和第一个区间才算是连接上了。
while (i <= two) {
// 如果遇到nums[i] == 0 那么就将nums[i]和第二个区间的第一个数交换
if (nums[i] == 0) {
swap(nums, i, zero);
i++;
zero++;
} else if (nums[i] == 1) {
i++;
} else {
// 如果遇到nums[i] == 2就将nums[i]和第三个区间的第一个数前面的那个数交换。
// 按照我们区间的定义,索引two位置就是第三个区间第一个数前面的那个数所在。
// 这里特别注意,在交换完索引位置i和索引位置two的元素后,i不能直接+1。
// 因为交换过来的数可不一定是1,要是其他的数,直接移动i的位置,在这个区间就掺杂了其他数。
swap(nums, i, two);
two--;
}
}
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
复杂度分析:
- 时间复杂度:O(N),这里 N 是输入数组的长度;
- 空间复杂度:O(1)。
88. 合并两个有序数组⭐
给你两个按 非递减顺序 排列的整数数组nums1和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你合并 nums2 到 nums1 中,使合并后的数组同样按非递减顺序排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,
后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
// 题目说了nums1数组的长度为m+n,从两个数组的最后开始比较较大的,然后放在nums1数组额末尾。
int i = m - 1, j = n - 1, k = m + n - 1;
// 因为根据题意是要将nums2数组中的元素合并到nums1中
// 那么当nums2中的元素处理完了,也就合并完了。
while (j >= 0) {
// i < 0 说明nums1中需要合并的元素已经处理完了,接下来直接将nums2中的元素
// 移动到nums1中即可
if (i < 0 || nums2[j] >= nums1[i]) {
nums1[k--] = nums2[j--];
} else {
nums1[k--] = nums1[i--];
}
}
}
}
剑指 Offer 51. 数组中的逆序对⭐⭐⭐⭐
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
输入: [7,5,6,4]
输出: 5
暴力解法:
class Solution {
public int reversePairs(int[] nums) {
int count = 0;
int len = nums.length;
for (int i = 0; i < len - 1; i++) {
for (int j = i + 1; j < len; j++) {
if (nums[i] > nums[j]) {
count++;
}
}
}
return count;
}
}
归并排序解法:

顺序数组的逆序对总数为0,倒序数组的逆序对总数达到最大,因此掌握数组的有序性可以一下子数出逆序对的总数。
我们使用归并排序一边排序一边计算逆序对的数量。
- 在第 2 个数组里的元素归并回去的时候,数出第 1 个数组里还没有归并回去的元素的个数;
- 第 1 个数组里还没有归并回去的元素,比当前第 2 个数组归并回去的元素要大。
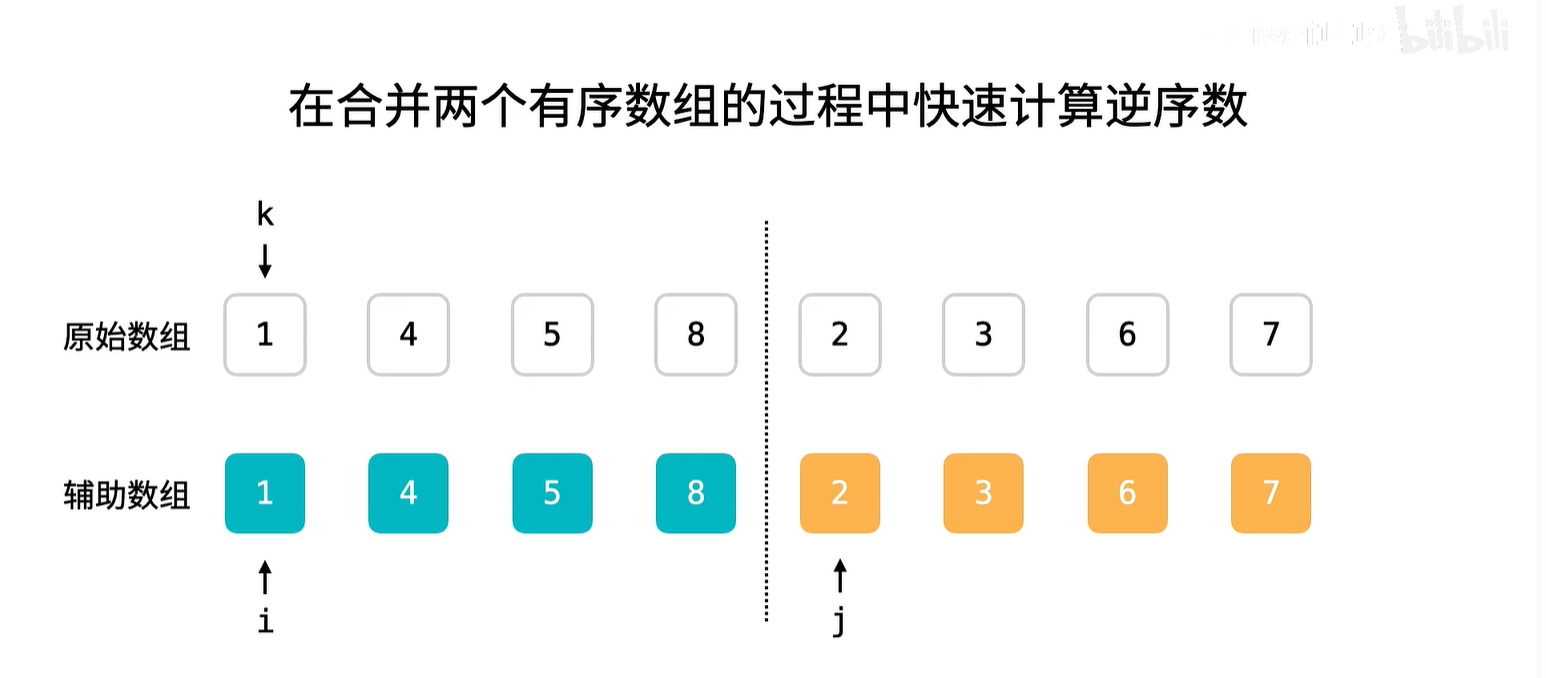
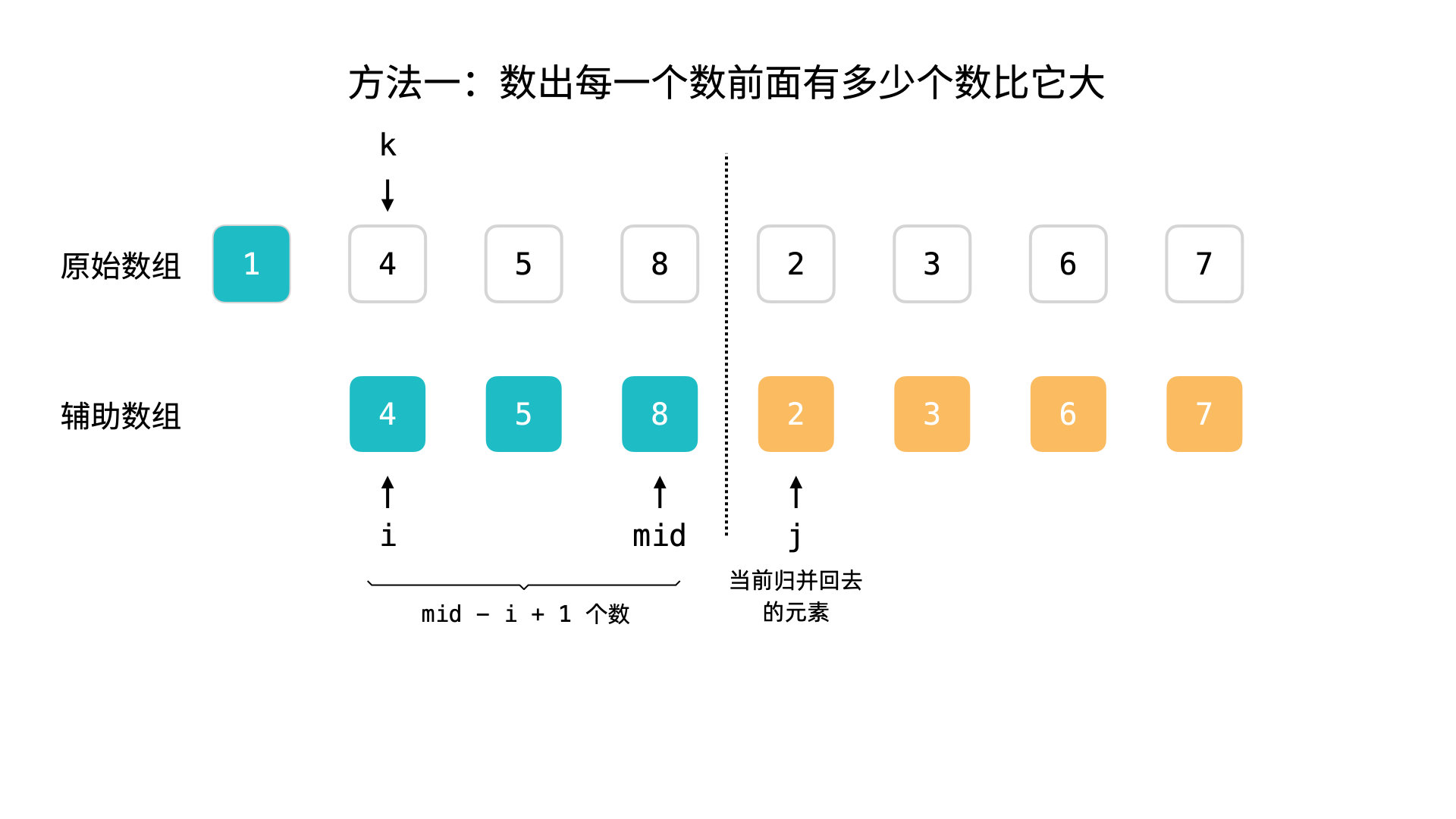
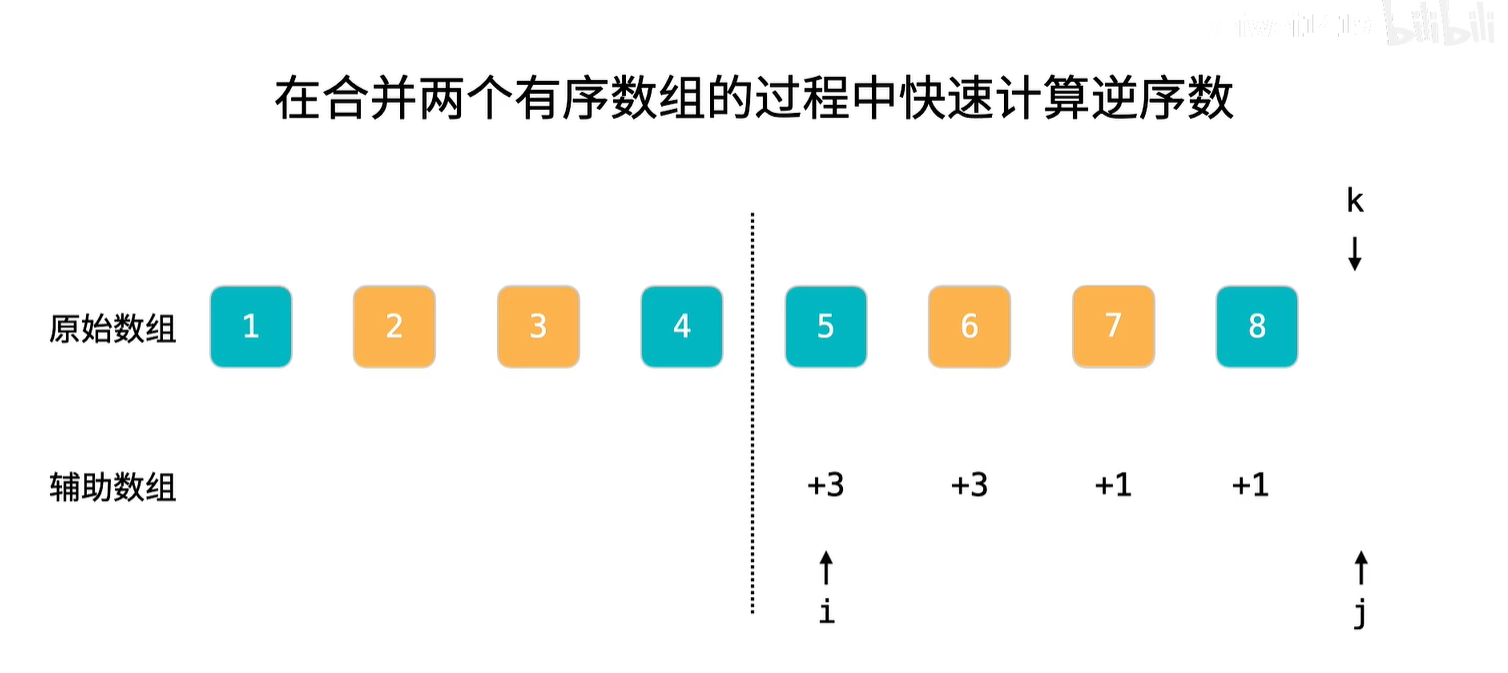
在 j 指向的元素赋值回去的时候,给计数器加上 mid - i + 1,比如这里将2归并回去,前面数组剩余的元素4 5 8都比2大,是逆序对。
就是在第二个数组的元素归并回去的时候,一下子数出第一个数组还没有归并回去的元素的个数。
class Solution {
public int reversePairs(int[] nums) {
int len = nums.length;
// 当数组的长度为0或1时不存在逆序对
if (len < 2) {
return 0;
}
int[] temp = new int[len];
return reversePairs(nums, 0, len - 1, temp);
}
private int reversePairs(int[] nums, int left, int right, int[] temp) {
if (left == right) {
return 0;
}
int mid = (left + right) / 2;
int leftPairs = reversePairs(nums, left, mid, temp);
int rightPairs = reversePairs(nums, mid + 1, right, temp);
if (nums[mid] <= nums[mid + 1]) {
return leftPairs + rightPairs;
}
int crossPairs = merge(nums, left, mid, right, temp);
return leftPairs + rightPairs + crossPairs;
}
private int merge(int[] nums, int left, int mid, int right, int[] temp) {
for (int i = left; i <= right; i++) {
temp[i] = nums[i];
}
// 分别用i和j指向两个有序数组的开始位置。
int i = left;
int j = mid + 1;
int k = left;
int count = 0;
// 你敢不敢重写?
while (i <= mid && j <= right) {
if (temp[i] <= temp[j]) {
nums[k++] = temp[i++];
} else {
nums[k++] = temp[j++];
// 右边数组的元素a归并回去时,左边数组还没有归并回去的元素个数。就是归并a时发现的逆序对个数。
count += (mid - i + 1);
}
}
while (i > mid && j <= right) {
nums[k++] = temp[j++];
}
while (j > right && i <= mid) {
nums[k++] = temp[i++];
}
return count;
}
}
315. 计算右侧小于当前元素的个数⭐⭐⭐⭐
给你一个整数数组 nums ,按要求返回一个新数组 counts 。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
输入:nums = [5,2,6,1]
输出:[2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1)
2 的右侧仅有 1 个更小的元素 (1)
6 的右侧有 1 个更小的元素 (1)
1 的右侧有 0 个更小的元素
class Solution {
private class Pair {
int val;
int index;
public Pair(int val, int index) {
this.val = val;
this.index = index;
}
}
Pair[] temp;
Pair[] arr;
int[] count;
public List<Integer> countSmaller(int[] nums) {
int len = nums.length;
temp = new Pair[len];
arr = new Pair[len];
count = new int[len];
for (int i = 0; i < len; i++) {
arr[i] = new Pair(nums[i], i);
}
sort(nums, 0, len - 1);
List<Integer> res = new ArrayList<>();
for (int cnt : count) {
res.add(cnt);
}
return res;
}
private void sort(int[] nums, int begin, int end) {
if (begin == end) {
return;
}
int mid = begin + (end - begin) / 2;
sort(nums, begin, mid);
sort(nums, mid + 1, end);
merge(nums, begin, mid, end);
}
private void merge(int[] nums, int begin, int mid, int end) {
for (int i = begin; i <= end; i++) {
temp[i] = arr[i];
}
int li = begin;
int le = mid;
int ri = mid + 1;
int re = end;
int k = begin;
while (li <= le && ri <= re) {
if (temp[li].val <= temp[ri].val) {
count[temp[li].index] += ri - mid - 1;
arr[k++] = temp[li++];
} else {
arr[k++] = temp[ri++];
}
}
while (li > le && ri <= re) {
arr[k++] = temp[ri++];
}
while (ri > re && li <= le) {
count[temp[li].index] += ri - mid - 1;
arr[k++] = temp[li++];
}
}
}
493. 翻转对⭐⭐⭐⭐
给定一个数组 nums ,如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个重要翻转对。
你需要返回给定数组中的重要翻转对的数量。
注意:
- 给定数组的长度不会超过50000;
- 输入数组中的所有数字都在32位整数的表示范围内。
其实315题也可以在合并之前求出nums[i] > nums[j]的数量,但是315题的数据量大很多,很有可能会超时。这个题数组长度不超过50000。
class Solution {
int[] temp;
int count;
public int reversePairs(int[] nums) {
int len = nums.length;
temp = new int[len];
sort(nums, 0, len - 1);
return count;
}
private void sort(int[] nums, int begin, int end) {
if (begin == end) {
return;
}
int mid = begin + (end - begin) / 2;
sort(nums, begin, mid);
sort(nums, mid + 1, end);
merge(nums, begin, mid, end);
}
private void merge(int[] nums, int begin, int mid, int end) {
for (int i = begin; i <= end; i++) {
temp[i] = nums[i];
}
int li = begin;
int le = mid;
int ri = mid + 1;
int re = end;
int j = mid + 1;
// 为什么要用归并?
// 因为归并会使数组慢慢的变有序
// 变有序了就会使满足(long)nums[i] > (long)nums[j] * 2越来越少。
// 因为前面的数更小,不可能会出现这种情况了。
// 但是其实最主要的思想还是分治的思想,分而治之。不断地拆分问题。
// 翻转对变为0只是一个结束条件,主要还是在归并排序之后带来的有序性方便我们找到翻转对。
for (int i = li; i <= le; i++) {
while (j <= re && (long)nums[i] > (long)nums[j] * 2) {
j++;
}
count += j - mid - 1;
}
for (int k = li; k <= re; k++) {
if (li == le + 1) {
nums[k] = temp[ri++];
} else if (ri == re + 1) {
nums[k] = temp[li++];
} else if (temp[li] <= temp[ri]) {
nums[k] = temp[li++];
} else if (temp[li] > temp[ri]) {
nums[k] = temp[ri++];
}
}
}
}
327. 区间和的个数⭐⭐⭐⭐
给你一个整数数组 nums 以及两个整数 lower 和 upper 。求数组中,值位于范围 [lower, upper] (包含 lower 和 upper)之内的 区间和的个数 。
区间和 S(i, j) 表示在 nums 中,位置从 i 到 j 的元素之和,包含 i 和 j (i ≤ j)。
输入:nums = [-2,5,-1], lower = -2, upper = 2
输出:3
解释:存在三个区间:[0,0]、[2,2] 和 [0,2] ,对应的区间和分别是:-2 、-1 、2 。
首先求出nums数组的前缀和数组,然后对前缀和进行归并排序的同时,判断
class Solution {
private int lower, upper;
public int countRangeSum(int[] nums, int lower, int upper) {
this.lower = lower;
this.upper = upper;
// 构建前缀和数组,注意 int 可能溢出,用 long 存储
long[] preSum = new long[nums.length + 1];
for (int i = 0; i < nums.length; i++) {
preSum[i + 1] = (long) nums[i] + preSum[i];
}
// 对前缀和数组进行归并排序
sort(preSum);
return count;
}
private long[] temp;
public void sort(long[] nums) {
temp = new long[nums.length];
sort(nums, 0, nums.length - 1);
}
private void sort(long[] nums, int lo, int hi) {
if (lo == hi) {
return;
}
int mid = lo + (hi - lo) / 2;
sort(nums, lo, mid);
sort(nums, mid + 1, hi);
merge(nums, lo, mid, hi);
}
private int count = 0;
private void merge(long[] nums, int lo, int mid, int hi) {
for (int i = lo; i <= hi; i++) {
temp[i] = nums[i];
}
// 在合并有序数组之前加点私货(这段代码会超时)
// for (int i = lo; i <= mid; i++) {
// for (int j = mid + 1; j <= hi; k++) {
// // 寻找符合条件的 nums[j]
// long delta = nums[j] - nums[i];
// if (delta <= upper && delta >= lower) {
// count++;
// }
// }
// }
// 归并排序会让前缀和数组越来越有序
// 这道题前缀和数组变得有序并没有使得区间和在[lower, upper]的区间个数更少。
// 这题前缀和数组变得有序,会让在求满足条件的区间时,[start, end)会一直向右滑动。
// 不用每次都重新从mid + 1开始判断。
// 我们可以维护一个区间:对于的一个元素x,先找到右边的下界,然后找到右边的上界,假设满足区间为 [a, b]。
// 对于下一个元素 y ,一定满足 x <= y 且右边的下界一定 >= a,右边的上界一定 >= b。满足条件的区间可能就是[a + x, b + y]。
// 主要还是分治的思想,归并排序带来的有序只是为了在搜索满足条件的区间时不用从mid + 1开始重新判断。
// 进行效率优化
// 维护左闭右开区间 [start, end) 中的元素和 nums[i] 的差在 [lower, upper] 中
int start = mid + 1, end = mid + 1;
for (int i = lo; i <= mid; i++) {
// 如果 nums[i] 对应的区间是 [start, end),
// 那么 nums[i+1] 对应的区间一定会整体右移,类似滑动窗口。
while (start <= hi && nums[start] - nums[i] < lower) {
start++;
}
while (end <= hi && nums[end] - nums[i] <= upper) {
end++;
}
count += end - start;
}
// 数组双指针技巧,合并两个有序数组
int i = lo, j = mid + 1;
for (int p = lo; p <= hi; p++) {
if (i == mid + 1) {
nums[p] = temp[j++];
} else if (j == hi + 1) {
nums[p] = temp[i++];
} else if (temp[i] > temp[j]) {
nums[p] = temp[j++];
} else {
nums[p] = temp[i++];
}
}
}
}
217. 存在重复元素
给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ,返回 true ;如果数组中每个元素互不相同,返回 false 。
class Solution {
public boolean containsDuplicate(int[] nums) {
Arrays.sort(nums);
for (int i = 1; i < nums.length; i++) {
if (nums[i] == nums[i - 1]) {
return true;
}
}
return false;
}
}
238. 除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请不要使用除法,且在 O(n) 时间复杂度,O(1) 空间复杂度内完成此题。
class Solution {
public int[] productExceptSelf(int[] nums) {
int len = nums.length;
// 用两个数组分别存放nums数组中每一个元素左右两边元素的乘积
int[] leftArray = new int[len];
int[] rightArray = new int[len];
int[] res = new int[len];
// nums数组第一个元素左边乘积初始化为1
leftArray[0] = 1;
// nums数组最后一个元素右边乘积初始化为1
rightArray[len - 1] = 1;
// 遍历求出nums数组中每一个元素左边所有元素的乘积
for (int i = 1; i <= len - 1; i++) {
leftArray[i] = leftArray[i - 1] * nums[i - 1];
}
// 遍历求出nums数组中每一个元素右边所有元素的乘积
for (int i = len - 2; i >= 0; i--) {
rightArray[i] = rightArray[i + 1] * nums[i + 1];
}
// 每个元素左边所有元素的乘积再乘以右边所有元素的乘积就是这个元素处自身以外数组的乘积
for (int i = 0; i < len; i++) {
res[i] = leftArray[i] * rightArray[i];
}
return res;
}
}
o(1)空间复杂度解法
class Solution {
public int[] productExceptSelf(int[] nums) {
int len = nums.length;
int[] res = new int[len];
int left = 1;
int right = 1;
for (int i = 0; i <= len - 1; i++) {
res[i] = left;
left = res[i] * nums[i];
}
for (int i = len - 1; i >= 0; i--) {
res[i] = res[i] * right;
right = right * nums[i];
}
return res;
}
}
283. 移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
解法一:
把非0的往前挪,挪完之后,后面的就都是0了,然后在用0覆盖后面的。这种是最容易理解也是最容易想到的,代码比较简单,这里就以示例为例画个图来看下:

class Solution {
public void moveZeroes(int[] nums) {
int index = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] != 0) {
nums[index++] = nums[i];
}
}
while (index < nums.length) {
nums[index++] = 0;
}
}
}
解法二:不直接覆盖而是交换,后面就不用补0了。
class Solution {
public void moveZeroes(int[] nums) {
int i = 0;
for (int j = 0; j < nums.length; j++) {
if (nums[j] != 0) {
int temp = nums[j];
nums[j] = nums[i];
nums[i] = temp;
i++;
}
}
}
}
解法三:先删除0,后面再补零
class Solution {
public void moveZeroes(int[] nums) {
int p = removeElement(nums, 0);
for (; p < nums.length; p++) {
nums[p] = 0;
}
}
public int removeElement(int[] nums, int val) {
int left = 0, right = 0;
while (right < nums.length) {
if (nums[right] != val) {
nums[left] = nums[right];
left++;
}
right++;
}
return left;
}
}
73. 矩阵置零
给定一个 m x n的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
class Solution {
public void setZeroes(int[][] matrix) {
int[] row = new int[matrix.length];
int[] column = new int[matrix[0].length];
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[0].length; j++) {
// 当遍历二维矩阵出现值为0的元素时,记录下这个元素的行和列。
if (matrix[i][j] == 0) {
row[i] = 1;
column[j] = 1;
}
}
}
// 先遍历行,如果这一行没有被标记,就不用处理,继续查看下一行。
for (int i = 0; i < matrix.length; i++) {
if (row[i] == 1) {
for (int j = 0; j < matrix[0].length; j++) {
matrix[i][j] = 0;
}
}
}
// 先遍历列,如果这一列没有被标记,就不用处理,继续查看下一列。
for (int j = 0; j < matrix[0].length; j++) {
if (column[j] == 1) {
for (int i = 0; i < matrix.length; i++) {
matrix[i][j] = 0;
}
}
}
}
}
class Solution {
public void setZeroes(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
// 1. 扫描「首行」和「首列」记录「首行」和「首列」是否该被置零
boolean r0 = false, c0 = false;
for (int i = 0; i < m; i++) {
if (matrix[i][0] == 0) {
c0 = true;
break;
}
}
for (int j = 0; j < n; j++) {
if (matrix[0][j] == 0) {
r0 = true;
break;
}
}
// 2.1 扫描「非首行首列」的位置,如果发现零,将需要置零的信息存储到该行的「最左方」和「最上方」的格子内
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (matrix[i][j] == 0) {
matrix[i][0] = matrix[0][j] = 0;
}
}
}
// 2.2 根据刚刚记录在「最左方」和「最上方」格子内的置零信息,进行「非首行首列」置零
for (int j = 1; j < n; j++) {
if (matrix[0][j] == 0) {
for (int i = 1; i < m; i++) {
matrix[i][j] = 0;
}
}
}
for (int i = 1; i < m; i++) {
if (matrix[i][0] == 0) {
for (int j = 1; j < n; j++) {
matrix[i][j] = 0;
}
}
}
// 3. 根据最开始记录的「首行」和「首列」信息,进行「首行首列」置零
if (c0) {
for (int i = 0; i < m; i++) {
matrix[i][0] = 0;
}
}
if (r0) {
Arrays.fill(matrix[0], 0);
}
}
}
class Main {
public static void main(String args[]) {
int[][] matrix = new int[][]{
new int[]{1, 1, 1},
new int[]{1, 0, 1},
new int[]{1, 1, 1}
};
Solution solution = new Solution();
solution.setZeroes(matrix);
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[0].length; j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
}
}
396. 旋转函数
给定一个长度为 n 的整数数组 nums 。
假设 arrk 是数组 nums 顺时针旋转 k 个位置后的数组,我们定义 nums 的 旋转函数 F 为:
- F(k) = 0 * arrk[0] + 1 * arrk[1] + ... + (n - 1) * arrk[n - 1]
返回 F(0), F(1), ..., F(n-1)中的最大值。
生成的测试用例让答案符合 32 位 整数。
示例:
输入: nums = [4,3,2,6]
输出: 26
解释:
F(0) = (0 * 4) + (1 * 3) + (2 * 2) + (3 * 6) = 0 + 3 + 4 + 18 = 25
F(1) = (0 * 6) + (1 * 4) + (2 * 3) + (3 * 2) = 0 + 4 + 6 + 6 = 16
F(2) = (0 * 2) + (1 * 6) + (2 * 4) + (3 * 3) = 0 + 6 + 8 + 9 = 23
F(3) = (0 * 3) + (1 * 2) + (2 * 6) + (3 * 4) = 0 + 2 + 12 + 12 = 26
所以 F(0), F(1), F(2), F(3) 中的最大值是 F(3) = 26 。
解题思路:
F(0) = 0*A[0]+1*A[1]+2*A[2]+3*A[3]
F(1) = 0*A[3]+1*A[0]+2*A[1]+3*A[2]
F(2) = 0*A[2]+1*A[3]+2*A[0]+3*A[1]
F(3) = 0*A[1]+1*A[2]+2*A[3]+3*A[0]
F(1)-F(0) = A[0]+A[1]+A[2]-3*A[3]
F(2)-F(1) = A[0]+A[1]+A[3]-3*A[2]
F(3)-F(2) = A[0]+A[2]+A[3]-3*A[1]
其中 我们定于sumA = A[0]+A[1]+A[2]+A[3],有意思了
比如其中F(3)-F(2) = A[0]+A[2]+A[3]-3*A[1]= sumA - 4*A[1]
class Solution {
public int maxRotateFunction(int[] nums) {
int n = nums.length;
int sum = 0, pre = 0;
for (int i = 0; i < n; i++) {
sum += nums[i];
pre += i * nums[i];
}
int max = pre;
for (int i = n - 1; i >= 0; i--) {
pre = (pre + sum) - n * nums[i];
max = Math.max(max, pre);
}
return max;
}
}
528. 按权重随机选择(前缀和+二分)⭐⭐⭐⭐
给你一个 下标从 0 开始 的正整数数组 w ,其中 w[i] 代表第 i 个下标的权重。
请你实现一个函数 pickIndex ,它可以 随机地 从范围 [0, w.length - 1] 内(含 0 和 w.length - 1)选出并返回一个下标。
选取下标 i 的 概率 为 w[i] / sum(w) 。
例如,对于 w = [1, 3],挑选下标 0 的概率为 1 / (1 + 3) = 0.25 (即,25%),而选取下标 1 的概率为 3 / (1 + 3) = 0.75(即,75%)。
参考题解:https://labuladong.gitee.io/algo/2/20/30/
假设给你输入的权重数组是 w = [1,3,2,1],我们想让概率符合权重,那么可以抽象一下,根据权重画出这么一条彩色的线段:

如果我在线段上面随机丢一个石子,石子落在哪个颜色上,我就选择该颜色对应的权重索引,那么每个索引被选中的概率是不是就是和权重相关联了?
所以,你再仔细看看这条彩色的线段像什么?这不就是 前缀和数组 嘛:

那么接下来,如何模拟在线段上扔石子?
当然是随机数,比如上述前缀和数组 preSum,取值范围是 [1, 7],那么我生成一个在这个区间的随机数 target = 5,就好像在这条线段中随机扔了一颗石子:

还有个问题,preSum 中并没有 5 这个元素,我们应该选择比 5 大的最小元素,也就是 6,即 preSum 数组的索引 3:

如何快速寻找数组中大于等于目标值的最小元素? 二分搜索算法 就是我们想要的。
到这里,这道题的核心思路就说完了,主要分几步:
1、根据权重数组 w 生成前缀和数组 preSum。
2、生成一个取值在 preSum 之内的随机数,用二分搜索算法寻找大于等于这个随机数的最小元素索引。
3、最后对这个索引减一(因为前缀和数组有一位索引偏移),就可以作为权重数组的索引,即最终答案:

上述思路应该不难理解,但是写代码的时候坑可就多了。
要知道涉及开闭区间、索引偏移和二分搜索的题目,需要你对算法的细节把控非常精确,否则会出各种难以排查的 bug。
下面来抠细节,继续前面的例子:

就比如这个 preSum 数组,你觉得随机数 target 应该在什么范围取值?闭区间 [0, 7] 还是左闭右开 [0, 7)?
都不是,应该在闭区间 [1, 7] 中选择,因为前缀和数组中 0 本质上是个占位符,仔细体会一下:

接下来,在 preSum 中寻找大于等于 target 的最小元素索引,应该用什么品种的二分搜索?搜索左侧边界的还是搜索右侧边界的?
实际上应该使用搜索左侧边界的二分搜索:
// 搜索左侧边界的二分搜索
int leftBound(int[] nums, int target) {
if (nums.length == 0) return -1;
int left = 0, right = nums.length;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
return left;
}
前文 二分搜索详解 着重讲了数组中存在目标元素重复的情况,没仔细讲目标元素不存在的情况,这里补充一下。
当目标元素 target 不存在数组 nums 中时,搜索左侧边界的二分搜索的返回值可以做以下几种解读:
1、返回的这个值是 nums 中大于等于 target 的最小元素索引;
2、返回的这个值是 target 应该插入在 nums 中的索引位置;
3、返回的这个值是 nums 中小于 target 的元素个数。
比如在有序数组 nums = [2,3,5,7] 中搜索 target = 4,搜索左边界的二分算法会返回 2,你带入上面的说法,都是对的。
所以以上三种解读都是等价的,可以根据具体题目场景灵活运用,显然这里我们需要的是第一种。
综上,我们可以写出最终解法代码:
class Solution {
// 前缀和数组
private int[] preSum;
private Random rand = new Random();
public Solution(int[] w) {
int n = w.length;
// 构建前缀和数组,偏移一位留给 preSum[0]
preSum = new int[n + 1];
preSum[0] = 0;
// preSum[i] = sum(w[0..i-1])
for (int i = 1; i <= n; i++) {
preSum[i] = preSum[i - 1] + w[i - 1];
}
}
public int pickIndex() {
int n = preSum.length;
// 在闭区间 [1, preSum[n - 1]] 中随机选择一个数字。
// rand.nextInt(n)这个函数是这样的返回[0, n)之间的一个随机数,也就是包括0,不包括指定的数n。
// rand.nextInt(preSum[n - 1]) 的范围是[0, preSum[n - 1] - 1] 加上1之后就变为了
// [1, preSum[n - 1]]。
int target = rand.nextInt(preSum[n - 1]) + 1;
// 获取 target 在前缀和数组 preSum 中的索引
// 别忘了前缀和数组 preSum 和原始数组 w 有一位索引偏移
return left_bound(preSum, target) - 1;
}
// 搜索左侧边界的二分搜索
int left_bound(int[] nums, int target) {
int left = 0, right = nums.length;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
return left;
}
}
380. O(1) 时间插入、删除和获取随机元素⭐⭐
实现RandomizedSet 类:
- RandomizedSet() 初始化 RandomizedSet 对象;
- bool insert(int val) 当元素 val 不存在时,向集合中插入该项,并返回 true ;否则,返回 false ;
- bool remove(int val) 当元素 val 存在时,从集合中移除该项,并返回 true ;否则,返回 false ;
- int getRandom() 随机返回现有集合中的一项(测试用例保证调用此方法时集合中至少存在一个元素);
- 每个元素应该有 相同的概率 被返回。
你必须实现类的所有函数,并满足每个函数的 平均 时间复杂度为 O(1) 。
基本思路就是空间换时间
class RandomizedSet {
// 存放元素
List<Integer> nums;
// 记录每个元素在nums中的索引
Map<Integer, Integer> indexes;
Random random;
public RandomizedSet() {
nums = new ArrayList<>();
indexes = new HashMap<>();
random = new Random();
}
public boolean insert(int val) {
// 存在,不插入
if (indexes.containsKey(val)) {
return false;
}
// 获取val的索引,因为要插入到最后。
int valIndex = nums.size();
// val为key valIndex为value 存入map中
indexes.put(val, valIndex);
// 记录元素
nums.add(val);
return true;
}
public boolean remove(int val) {
// 不存在,不删除
if (!indexes.containsKey(val)) {
return false;
}
// 拿到当前值的索引
int valIndex = indexes.get(val);
// 拿到当前末尾的数
int lastNum = nums.get(nums.size() - 1);
// 把要删除数val索引valIndex的值,替换为数组的最后一个数lastNum
nums.set(valIndex, lastNum);
// 索引map中,把末位数字的索引值,更新为要删除数字val的索引值
indexes.put(lastNum, valIndex);
// 数组移除末尾元素
nums.remove(nums.size() - 1);
// 索引集合移除要删除的key
indexes.remove(val);
return true;
}
public int getRandom() {
// 从[0, nums.size())中随机选择一个索引。
int index = random.nextInt(nums.size());
return nums.get(index);
}
}
710. 黑名单中的随机数⭐⭐
给定一个整数 n 和一个 无重复 黑名单整数数组 blacklist 。设计一种算法,从 [0, n - 1] 范围内的任意整数中选取一个 未加入 黑名单 blacklist 的整数。任何在上述范围内且不在黑名单 blacklist 中的整数都应该有 同等的可能性 被返回。
优化你的算法,使它最小化调用语言 内置 随机函数的次数。
实现 Solution 类:
- Solution(int n, int[] blacklist) 初始化整数 n 和被加入黑名单 blacklist 的整数
- int pick() 返回一个范围为 [0, n - 1] 且不在黑名单 blacklist 中的随机整数
class Solution {
private final HashMap<Integer, Integer> mapping;
private final Random random;
private final int size;
public Solution(int n, int[] blacklist) {
mapping = new HashMap();
random = new Random();
size = n - blacklist.length;
// 先把黑名单中的数放在哈希表中
for (int black : blacklist) {
mapping.put(black, 666);
}
int last = n - 1;
for (int black : blacklist) {
// 如果黑名单中的数已经在后面部分了不用做处理,因为随机时取不到这里。
if (black > size - 1) {
continue;
}
// 如果last指向的位置就是黑名单中的数,此时不能做索引映射,应该找到第一个不是黑名单中的数。
while (mapping.containsKey(last)) {
last--;
}
// 用map来存储前n - blacklist.length个数中属于黑名单中的数和后面剩下的数中非黑名单中的数的映射关系。
mapping.put(black, last);
last--;
}
}
public int pick() {
int index = random.nextInt(size);
return mapping.containsKey(index) ? mapping.get(index) : index;
}
}
870. 优势洗牌(田忌赛马)
给定两个大小相等的数组 nums1 和 nums2,nums1 相对于 nums 的优势可以用满足 nums1[i] > nums2[i] 的索引 i 的数目来描述。
返回 nums1 的任意排列,使其相对于 nums2 的优势最大化。
输入:nums1 = [2,7,11,15], nums2 = [1,10,4,11]
输出:[2,11,7,15]
class Solution {
int[] advantageCount(int[] nums1, int[] nums2) {
int n = nums1.length;
// 给 nums2的元素进行 降序排序,但是不能直接再nums2中进行排序结果的存放。nums2必须保持原样。
PriorityQueue<int[]> maxpq = new PriorityQueue<>((int[] pair1, int[] pair2) -> {
return pair2[1] - pair1[1]; // 按照值来排序,可不是下标哦!
});
for (int i = 0; i < n; i++) {
// 用一个数组来存索引和值。
maxpq.offer(new int[]{i, nums2[i]});
}
// 给nums1升序排序。
Arrays.sort(nums1);
// nums1[left]是最小值,nums1[right]是最大值。
int left = 0, right = n - 1;
int[] res = new int[n];
while (!maxpq.isEmpty()) {
int[] pair = maxpq.poll();
// maxval是nums2中的最大值,i是对应索引。
int i = pair[0], maxval = pair[1];
if (maxval < nums1[right]) {
// 如果nums1[right]能胜过 maxval,那就自己上。
res[i] = nums1[right];
right--;
} else {
// 否则用最小值混一下,养精蓄锐。
res[i] = nums1[left];
left++;
}
}
return res;
}
}
912. 排序数组⭐⭐⭐⭐⭐
给你一个整数数组 nums,请你将该数组升序排列。
通过这道题来熟悉归并排序以及快速排序。
快速排序
单路快排:
单路快排将切分元素也就是轴点的右边分为了两个部分,一个区间是小于等于轴点元素的,另一个区间是大于轴点元素的。
class Solution {
public int[] sortArray(int[] nums) {
sort(nums, 0, nums.length - 1);
return nums;
}
private void sort(int[] nums, int begin, int end) {
// 这里为什么是end <= begin呢?
// 当begin到end区间只有两个元素时,返回的pivotIndex必定是这两个元素的下标之一,那么只有end <= begin才会保证递归退出。
if (end <= begin) {
return;
}
int pivotIndex = partition(nums, begin, end);
sort(nums, begin, pivotIndex - 1);
sort(nums, pivotIndex + 1, end);
}
private int partition(int[] nums, int begin, int end) {
int random = (int) (Math.random() * (end - begin));
swap(nums, begin, begin + random);
int pivot = nums[begin];
int j = begin;
// all num in [begin + 1, j] <= pivot 当初始化j = begin时 [begin + 1, j]是空区间。
// all num in (j, i) > pivot
for (int i = begin + 1; i <= end; i++) {
if (nums[i] <= pivot) {
j++;
swap(nums, i, j);
}
// 如果遇到nums[i] > pivot就不管,继续移动j就行。
}
// 最后将pivot = nums[begin]和第一个区间的最后一个数交换。
swap(nums, begin, j);
return j;
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
双路快排:

class Solution {
public int[] sortArray(int[] nums) {
sort(nums, 0, nums.length - 1);
return nums;
}
private void sort(int[] nums, int begin, int end) {
// 这里为什么是end <= begin呢?
// 当begin到end区间只有两个元素时,返回的pivotIndex必定是这两个元素的下标之一,那么只有end <= begin才会保证递归退出。
if (end <= begin) {
return;
}
int pivotIndex = partition(nums, begin, end);
sort(nums, begin, pivotIndex - 1);
sort(nums, pivotIndex + 1, end);
}
private int partition(int[] nums, int begin, int end) {
int random = (int) (Math.random() * (end - begin));
swap(nums, begin, begin + random);
int pivot = nums[begin];
int le = begin + 1;
int ge = end;
// all num in [begin + 1, le) <= pivot
// all num in (ge, end] >= pivot
while (true) {
while (le <= ge && nums[le] < pivot) {
le++;
}
while (le <= ge && nums[ge] > pivot) {
ge--;
}
if (le >= ge) {
break;
}
swap(nums, le, ge);
le++;
ge--;
}
swap(nums, begin, ge);
return ge;
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
三路快排:
将和轴点元素相同的数挤压到中间。
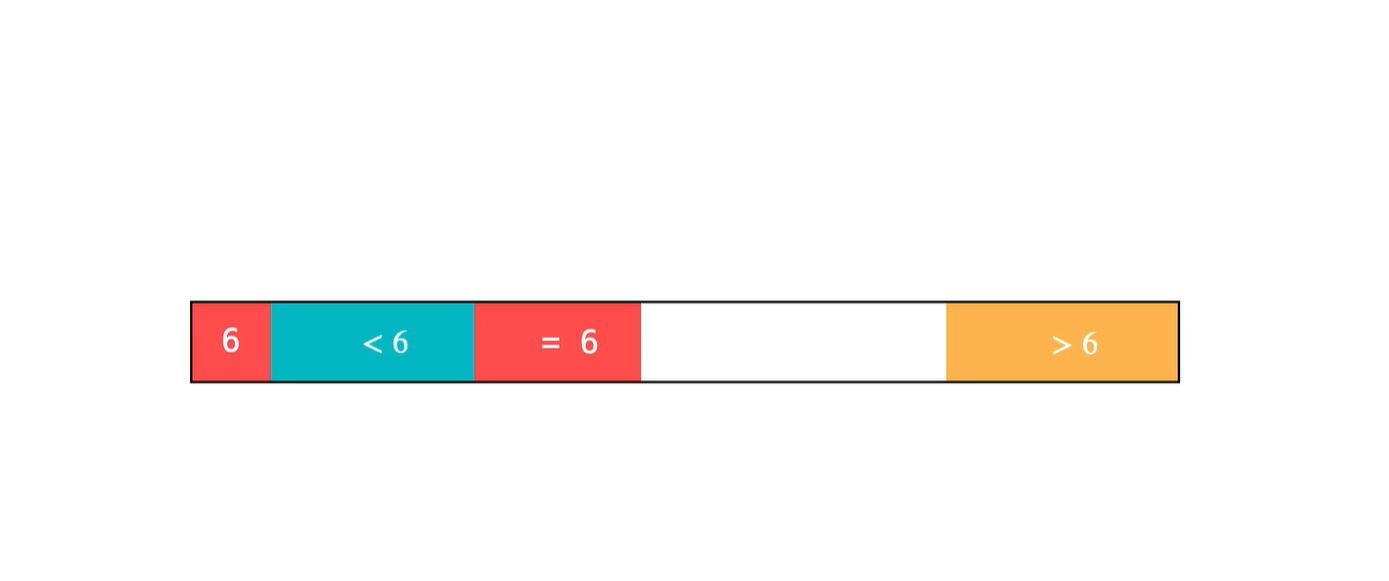
class Solution {
public int[] sortArray(int[] nums) {
sort(nums, 0, nums.length - 1);
return nums;
}
private void sort(int[] nums, int begin, int end) {
// 这里为什么是end <= begin呢?
// 当begin到end区间只有两个元素时,返回的pivotIndex必定是这两个元素的下标之一,那么只有end <= begin才会保证递归退出。
if (end <= begin) {
return;
}
int pivotIndex = partition(nums, begin, end);
sort(nums, begin, pivotIndex - 1);
sort(nums, pivotIndex + 1, end);
}
private int partition(int[] nums, int begin, int end) {
int random = (int) (Math.random() * (end - begin));
swap(nums, begin, begin + random);
// 轴点元素
int pivot = nums[begin];
int lt = begin + 1;
int gt = end;
int i = begin + 1;
// all num in [begin + 1, lt) < pivot
// all num in [lt, i) = pivot
// all num in (gt, end] > pivot
// 当i == gt时第二个区间和第三个区间并没有连接起来。
while (i <= gt) {
if (nums[i] < pivot) {
swap(nums, i, lt);
lt++;
i++;
} else if (nums[i] == pivot) {
i++;
} else if (nums[i] > pivot) {
swap(nums, i, gt);
gt--;
}
}
swap(nums, begin, lt - 1);
return lt - 1;
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
归并排序
class Solution {
int[] temp;
public int[] sortArray(int[] nums) {
temp = new int[nums.length];
sort(nums, 0, nums.length - 1);
return nums;
}
private void sort(int[] nums, int left, int right) {
if (left == right) {
return;
}
int mid = left + (right - left) / 2;
// 中间节点和前面部分在一起
sort(nums, left, mid);
sort(nums, mid + 1, right);
merge(nums, left, mid, right);
}
private void merge(int[] nums, int left, int mid, int right) {
int li = 0;
int le = mid - left;
int ri = mid + 1;
int re = right;
int ai = left;
for (int i = li; i <= le; i++) {
temp[i] = nums[i + left];
}
while (li <= le) {
if (ri > re || temp[li] < nums[ri]) {
nums[ai++] = temp[li++];
} else {
nums[ai++] = nums[ri++];
}
}
}
}
977. 有序数组的平方⭐
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
数组其实是有序的, 只不过负数平方之后可能成为最大数了。
那么数组平方的最大值就在数组的两端,不是最左边就是最右边,不可能是中间。
此时可以考虑双指针法了,i指向起始位置,j指向终止位置。
定义一个新数组result,和A数组一样的大小,让k指向result数组终止位置。
如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j];
如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i];
659. 分割数组为连续子序列⭐⭐⭐
给你一个按升序排序的整数数组 num(可能包含重复数字),请你将它们分割成一个或多个长度至少为 3 的子序列,其中每个子序列都由连续整数组成。
如果可以完成上述分割,则返回 true ;否则,返回 false 。
参考题解:https://labuladong.gitee.io/algo/4/33/125/
class Solution {
public boolean isPossible(int[] nums) {
// freq记录每个元素出现的次数。
HashMap<Integer, Integer> freq = new HashMap<>();
// need记录哪些元素可以被接到其他子序列后面。
HashMap<Integer, Integer> need = new HashMap<>();
// 统计 nums 中元素的频率
for (int n : nums) {
freq.put(n, freq.getOrDefault(n, 0) + 1);
}
for (int n : nums) {
// 已经被用到其他子序列中(排除)
if (freq.get(n) == 0) {
continue;
}
// 先判断 n 是否能接到其他子序列后面
if (need.getOrDefault(n, 0) > 0) {
// n 可以接到之前的某个序列后面
// 对n的需求减一
need.put(n, need.get(n) - 1);
freq.put(n, freq.get(n) - 1);
// 对n+1的需求加一
need.put(n + 1, need.getOrDefault(n + 1, 0) + 1);
// 先用containsKey判断存不存在,不存在返回null无法与0比较。
} else if (freq.getOrDefault(n, 0) > 0 && freq.getOrDefault(n + 1, 0) > 0 && freq.getOrDefault(n + 2, 0) > 0) {
// 将 n 作为开头,新建一个长度为 3 的子序列 [n, n+1, n+2]
freq.put(n, freq.get(n) - 1);
freq.put(n + 1, freq.get(n + 1) - 1);
freq.put(n + 2, freq.get(n + 2) - 1);
// 对 n + 3 的需求加一
need.put(n + 3, need.getOrDefault(n + 3, 0) + 1);
} else {
// 两种情况都不符合,则无法分配。
return false;
}
}
return true;
}
}
1296. 划分数组为连续数字的集合⭐⭐⭐
给你一个整数数组 nums 和一个正整数 k,请你判断是否可以把这个数组划分成一些由 k 个连续数字组成的集合。
如果可以,请返回 true;否则,返回 false。
输入:nums = [1,2,3,3,4,4,5,6], k = 4
输出:true
解释:数组可以分成 [1,2,3,4] 和 [3,4,5,6]。
class Solution {
public boolean isPossibleDivide(int[] nums, int k) {
Map<Integer, Integer> map = new HashMap<>();
PriorityQueue<Integer> q = new PriorityQueue<>();
for (int i : nums) {
map.put(i, map.getOrDefault(i, 0) + 1);
q.add(i);
}
while (!q.isEmpty()) {
int t = q.poll();
if (map.get(t) == 0) {
continue;
}
for (int i = 0; i < k; i++) {
int cnt = map.getOrDefault(t + i, 0);
if (cnt == 0) {
return false;
}
map.put(t + i, cnt - 1);
}
}
return true;
}
}
969. 煎饼排序
给你一个整数数组 arr ,请使用 煎饼翻转 完成对数组的排序。
一次煎饼翻转的执行过程如下:
- 选择一个整数 k ,1 <= k <= arr.length
- 反转子数组 arr[0...k-1](下标从 0 开始)
例如,arr = [3,2,1,4] ,选择 k = 3 进行一次煎饼翻转,反转子数组 [3,2,1] ,得到 arr = [1, 2, 3, 4] 。
以数组形式返回能使 arr 有序的煎饼翻转操作所对应的 k 值序列。任何将数组排序且翻转次数在 10 * arr.length 范围内的有效答案都将被判断为正确。
参考题解:https://labuladong.gitee.io/algo/4/33/126/
class Solution {
// 记录反转操作序列
LinkedList<Integer> res = new LinkedList<>();
List<Integer> pancakeSort(int[] cakes) {
sort(cakes, cakes.length);
return res;
}
void sort(int[] cakes, int n) {
// base case
if (n == 1) return;
// 寻找最大饼的索引
int maxCake = 0;
int maxCakeIndex = 0;
for (int i = 0; i < n; i++)
if (cakes[i] > maxCake) {
maxCakeIndex = i;
maxCake = cakes[i];
}
// 第一次翻转,将最大饼翻到最上面
reverse(cakes, 0, maxCakeIndex);
res.add(maxCakeIndex + 1);
// 第二次翻转,将最大饼翻到最下面
reverse(cakes, 0, n - 1);
res.add(n);
// 递归调用
sort(cakes, n - 1);
}
void reverse(int[] arr, int i, int j) {
while (i < j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
i++;
j--;
}
}
}
2363. 合并相似的物品
给你两个二维整数数组 items1 和 items2 ,表示两个物品集合。每个数组 items 有以下特质:
- items[i] = [valuei, weighti] 其中 valuei 表示第 i 件物品的 价值 ,weighti 表示第 i 件物品的 重量 。
- items 中每件物品的价值都是 唯一的 。
请你返回一个二维数组 ret,其中 ret[i] = [valuei, weighti], weighti 是所有价值为 valuei 物品的 重量之和 。
注意:ret 应该按价值 升序 排序后返回。
提示:
- 1 <= items1.length, items2.length <= 1000
- items1[i].length == items2[i].length == 2
- 1 <= valuei, weighti <= 1000
- items1 中每个 valuei 都是 唯一的 。
- items2 中每个 valuei 都是 唯一的 。
由提示可以看出价值和重量都不会超过1000,采用空间换时间的思路。
class Solution {
public List<List<Integer>> mergeSimilarItems(int[][] items1, int[][] items2) {
int[] a = new int[1001];
List l2 = new ArrayList();
for (int i = 0; i < items1.length; i++) {
a[items1[i][0]] += items1[i][1];
}
for (int i = 0; i < items2.length; i++) {
a[items2[i][0]] += items2[i][1];
}
for (int i = 0; i <= 1000; i++) {
if (a[i] != 0) {
List l1 = new ArrayList();
l1.add(i); // 价值
l1.add(a[i]); // 重量
l2.add(l1);
}
}
return l2;
}
}
二维数组
240. 搜索二维矩阵 II
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
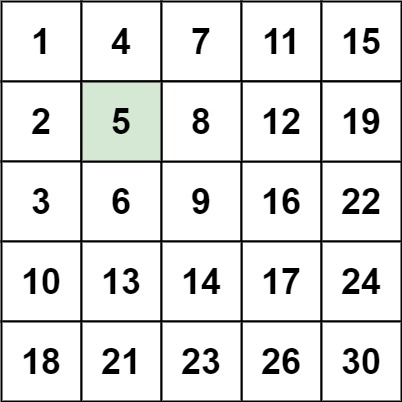
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int rows = matrix.length - 1;
int columns = matrix[0].length;
int row = 0;
int column = columns - 1;
while (row <= rows && column >= 0) {
int num = matrix[row][column];
if (num == target) {
return true;
} else if (num > target) {
column--;
} else if (num < target) {
row++;
}
}
return false;
}
}
48. 旋转图像
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
我们可以先将 n x n 矩阵 matrix 按照左上到右下的对角线进行镜像对称:

然后再对矩阵的每一行进行反转:

发现结果就是 matrix 顺时针旋转 90 度的结果:

class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
// 先沿斜对角线翻转
for (int i = 0; i < n; i++)
for (int j = 0; j < i; j++) {
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
// 再沿垂直竖线翻转
for (int i = 0; i < n; i++)
for (int j = 0, k = n - 1; j < k; j++, k--) {
int temp = matrix[i][k];
matrix[i][k] = matrix[i][j];
matrix[i][j] = temp;
}
}
}
54. 螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
// 初始化
int left = 0;
int top = 0;
int right = matrix[0].length - 1;
int bottom = matrix.length - 1;
List<Integer> res = new ArrayList<>();
// 循环打印
while (left <= right && top <= bottom) {
// 从左到右
for (int i = left; i <= right; i++) {
res.add(matrix[top][i]);
}
top++;
// 从上到下
for (int i = top; i <= bottom; i++) {
res.add(matrix[i][right]);
}
right--;
// 从右到左
for (int i = right; i >= left && top <= bottom; i--) {
res.add(matrix[bottom][i]);
}
bottom--;
// 从下到上
for (int i = bottom; i >= top && left <= right; i--) {
res.add(matrix[i][left]);
}
left++;
}
return res;
}
}
59. 螺旋矩阵 II
给你一个正整数 n ,生成一个包含 1 到 n^2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
class Solution {
public int[][] generateMatrix(int n) {
int left = 0;
int right = n - 1;
int top = 0;
int bottom = n - 1;
int[][] mat = new int[n][n];
int num = 1, tar = n * n;
while (num <= tar) {
for (int i = left; i <= right; i++) {
mat[top][i] = num++;
}
top++;
for (int i = top; i <= bottom; i++) {
mat[i][right] = num++;
}
right--;
for (int i = right; i >= left; i--) {
mat[bottom][i] = num++;
}
bottom--;
for (int i = bottom; i >= top; i--) {
mat[i][left] = num++;
}
left++;
}
return mat;
}
}
前缀和
待做题目:https://labuladong.gitee.io/algo/2/20/24/
303. 区域和检索 - 数组不可变
给定一个整数数组 nums,处理以下类型的多个查询:
- 计算索引 left 和 right (包含 left 和 right)之间的 nums 元素的 和 ,其中 left <= right
实现 NumArray 类:
- NumArray(int[] nums) 使用数组 nums 初始化对象;
- int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的 总和 ,包含 left 和 right 两点也就是 nums[left] + nums[left + 1] + ... + nums[right] 。
class NumArray {
// 前缀和数组
private int[] preSum;
/* 输入一个数组,构造前缀和 */
public NumArray(int[] nums) {
int len = nums.length;
// preSum[0] = 0,便于计算累加和
preSum = new int[len + 1];
// 计算 nums 的累加和
for (int i = 0; i < len; i++) {
preSum[i + 1] = preSum[i] + nums[i];
}
}
/* 查询闭区间 [left, right] 的累加和 */
public int sumRange(int left, int right) {
return preSum[right + 1] - preSum[left];
}
}
304. 二维区域和检索 - 矩阵不可变⭐⭐
给定一个二维矩阵 matrix,以下类型的多个请求:
- 计算其子矩形范围内元素的总和,该子矩阵的 左上角 为 (row1, col1) ,右下角 为 (row2, col2) 。
实现 NumMatrix 类:
- NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化;
- int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。
我们先从如何求出二维空间的 preSum[i] [j]。
我们定义 preSum[i] [j] 表示 从 [0,0] 位置到 [i, j] 位置的子矩形所有元素之和。
可以用下图帮助理解:
- S(O, D) = S(O, C) + S(O, B) - S(O, A) + D;
- S(O, D) = S(O,C) + S(O,B) − S(O,A) + D。
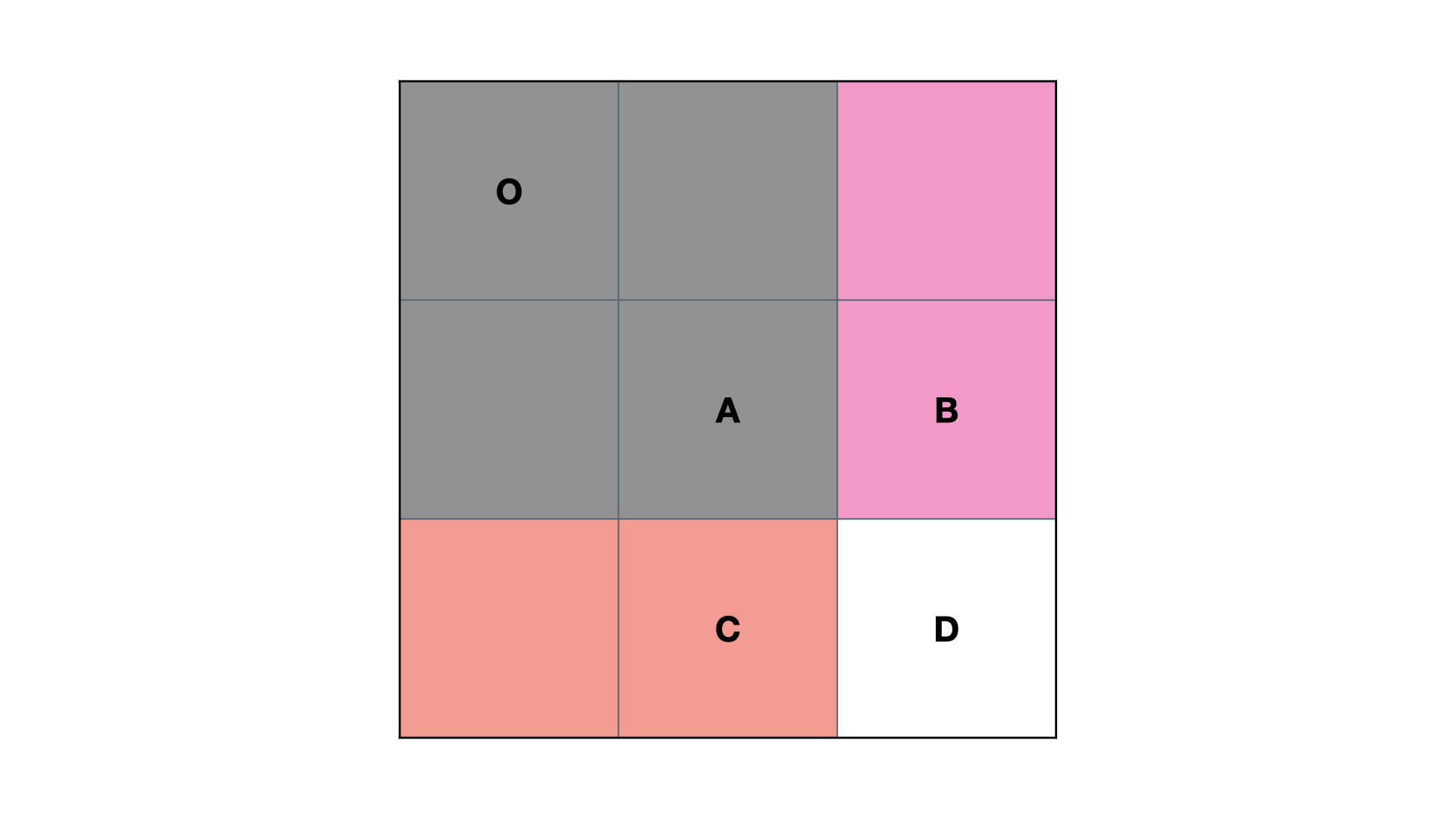
减去 S(O, A) 的原因是 S(O, C) 和 S(O, B) 中都有 S(O, A),即加了两次 S(O,A),所以需要减去一次 S(O, A)。
如果求 preSum[i] [j] 表示的话,对应了以下的递推公式:
preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] - preSum[i - 1][j - 1] + matrix[i][j];
前面已经求出了数组中从 [0, 0]位置到 [i, j]位置的 preSum。下面要利用 preSum[i] [j] 来快速求出任意子矩形的面积。
同样利用一张图来说明:
S(A,D) = S(O,D) − S(O,E) − S(O,F) + S(O,G)
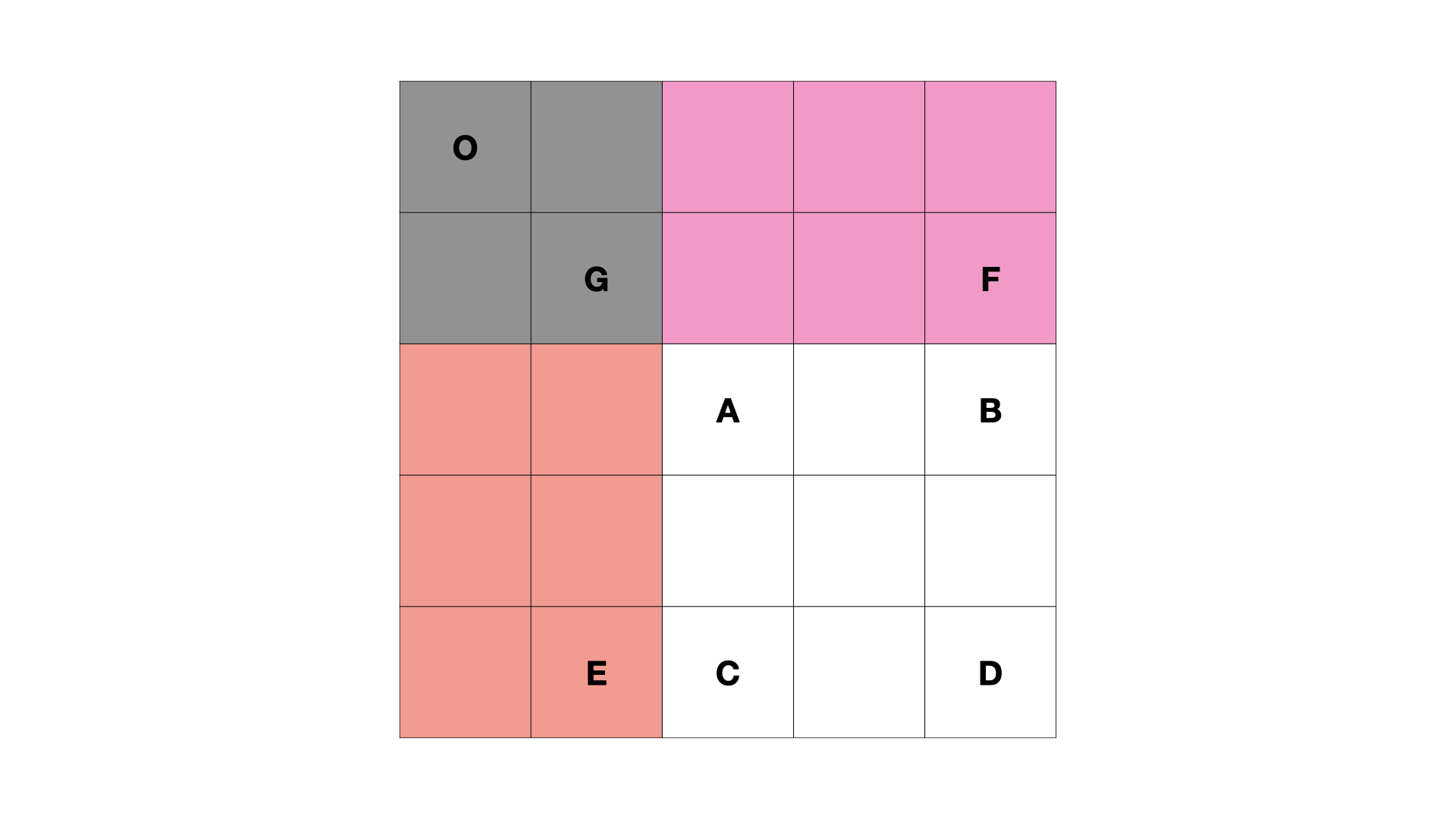
加上子矩形 S(O, G) 面积的原因是 S(O, E) 和 S(O, F) 中都有 S(O, G) ,即减了两次 S(O, G) ,所以需要加上一次 S(O, G) 。
class NumMatrix {
// 定义:preSum[i][j] 记录 matrix 中子矩阵 [0, 0, i-1, j-1] 的元素和。
private final int[][] preSum;
public NumMatrix(int[][] matrix) {
// m 是行数,n是列数。
int m = matrix.length, n = matrix[0].length;
// 构造前缀和矩阵。
preSum = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
// 计算每个矩阵 [0, 0, i, j] 的元素和。
preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] - preSum[i - 1][j - 1] + matrix[i - 1][j - 1];
}
}
}
// 计算子矩阵 [x1, y1, x2, y2] 的元素和。
public int sumRegion(int x1, int y1, int x2, int y2) {
// 目标矩阵之和由四个相邻矩阵运算获得。
return preSum[x2 + 1][y2 + 1] - preSum[x1][y2 + 1] - preSum[x2 + 1][y1] + preSum[x1][y1];
}
}
1314. 矩阵区域和
给你一个 m x n 的矩阵 mat 和一个整数 k ,请你返回一个矩阵 answer ,其中每个 answer[i] [j] 是所有满足下述条件的元素 mat[r] [c] 的和:
- i - k <= r <= i + k,
- j - k <= c <= j + k 且
- (r, c) 在矩阵内。
这题的意思是类似于一个矩形,(这个矩形大小会变),在数据矩阵上向右和向下滑动,每走一步,就会笼罩一个区域,计算这个区域里面值的和,类似于深度学习中
的卷积操作。
class Solution {
public int[][] matrixBlockSum(int[][] mat, int k) {
int m = mat.length, n = mat[0].length;
NumMatrix numMatrix = new NumMatrix(mat);
int[][] res = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// 左上角的坐标
int x1 = Math.max(i - k, 0);
int y1 = Math.max(j - k, 0);
// 右下角坐标
int x2 = Math.min(i + k, m - 1);
int y2 = Math.min(j + k, n - 1);
res[i][j] = numMatrix.sumRegion(x1, y1, x2, y2);
}
}
return res;
}
}
class NumMatrix {
// 定义:preSum[i][j] 记录 matrix 中子矩阵 [0, 0, i-1, j-1] 的元素和
private int[][] preSum;
public NumMatrix(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
if (m == 0 || n == 0) return;
// 构造前缀和矩阵
preSum = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
// 计算每个矩阵 [0, 0, i, j] 的元素和
preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] + matrix[i - 1][j - 1] - preSum[i - 1][j - 1];
}
}
}
// 计算子矩阵 [x1, y1, x2, y2] 的元素和
public int sumRegion(int x1, int y1, int x2, int y2) {
// 目标矩阵之和由四个相邻矩阵运算获得
return preSum[x2 + 1][y2 + 1] - preSum[x1][y2 + 1] - preSum[x2 + 1][y1] + preSum[x1][y1];
}
}
https://leetcode.cn/problems/subarray-sum-equals-k/solution/by-ac_oier-pttu/
前缀和其实我们很早之前就了解过的,我们求数列的和时,Sn = a1+a2+a3+...an,此时Sn就是数列的前 n 项和。例 S5 = a1 + a2 + a3 + a4 + a5; S2 = a1 + a2。所
以我们完全可以通过 S5 - S2 得到 a3 + a4 + a5 的值,这个过程就和我们做题用到的前缀和思想类似。我们的前缀和数组里保存的就是前 n 项的和。见下图:
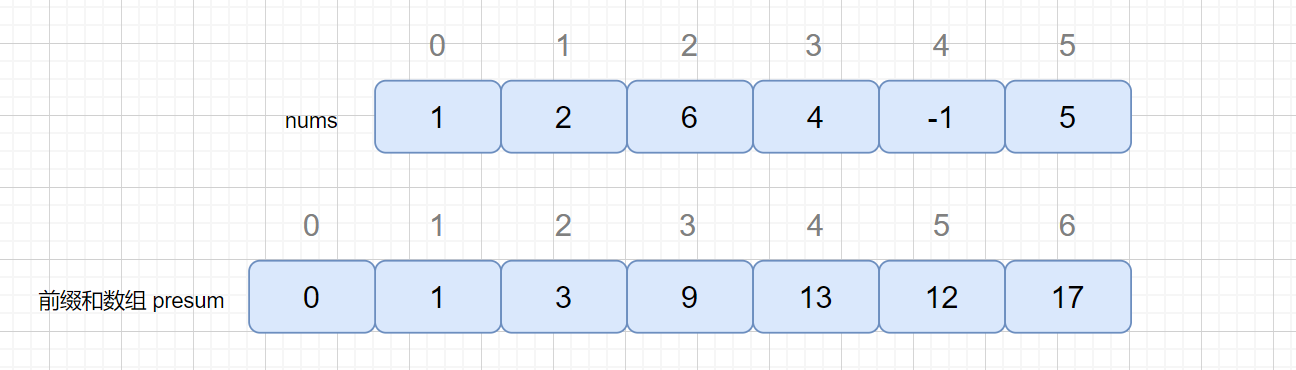
我们通过前缀和数组保存前 n 位的和,presum[1]保存的就是 nums 数组中前 1 位的和,也就是 presum[1] = nums[0], presum[2] = nums[0] + nums[1] =
presum[1] + nums[1]。依次类推,所以我们通过前缀和数组可以轻松得到每个区间的和。
例如我们需要获取 nums[2] 到 nums[4] 这个区间的和,我们则完全根据 presum 数组得到,是不是有点和我们之前说的字符串匹配算法中 BM,KMP 中的 next 数
组和 suffix 数组作用类似。那么我们怎么根据 presum 数组获取 nums[2] 到 nums[4] 区间的和呢?见下图:

好啦,我们已经了解了前缀和的解题思想了,我们可以通过下面这段代码得到我们的前缀和数组,非常简单。
for (int i = 0; i < nums.length; i++) {
presum[i + 1] = nums[i] + presum[i];
}
好啦,我们开始实战吧。
724. 寻找数组的中心下标
给你一个整数数组 nums ,请计算数组的 中心下标 。
数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1 。
class Solution {
public int pivotIndex(int[] nums) {
int preSum = 0;
// 求数组总和
for (int num : nums) {
preSum += num;
}
int leftSum = 0;
for (int i = 0; i < nums.length; i++) {
if (leftSum == preSum - leftSum - nums[i]) {
return i;
}
leftSum = leftSum + nums[i];
}
return -1;
}
}
class Solution {
public int pivotIndex(int[] nums) {
int end = 0;
int sum = 0;
int leftSum = 0;
for (int num : nums) {
sum += num;
}
while (end < nums.length) {
if (leftSum == sum - leftSum - nums[end]) {
return end;
}
leftSum += nums[end];
end++;
}
return -1;
}
}
560. 和为 K 的子数组的个数⭐
给你一个整数数组 nums 和一个整数 k ,请你统计并返回该数组中和为 k 的连续子数组的个数。
暴力:
class Solution {
public int subarraySum(int[] nums, int k) {
int len = nums.length;
int sum = 0;
int count = 0;
// 双重循环
for (int i = 0; i < len; ++i) {
for (int j = i; j < len; ++j) {
sum += nums[j];
// 发现符合条件的区间
if (sum == k) {
count++;
}
}
// 记得归零,重新遍历
sum = 0;
}
return count;
}
}
前缀和:
class Solution {
public int subarraySum(int[] nums, int k) {
// 前缀和数组
int[] preSum = new int[nums.length + 1];
for (int i = 0; i < nums.length; i++) {
// 这里需要注意,我们的前缀和是presum[1]开始填充的。
preSum[i + 1] = nums[i] + preSum[i];
}
// 统计个数。
int count = 0;
for (int i = 0; i < nums.length; ++i) {
for (int j = i; j < nums.length; ++j) {
// 注意偏移,因为我们的nums[2]到nums[4]等于presum[5] - presum[2]。
// 所以这样就可以得到nums[i,j]区间内的和。
if (preSum[j + 1] - preSum[i] == k) {
count++;
}
}
}
return count;
}
}
题目要求的是连续子数组的和等于k,也就是说在数组中某一个区间的和等于k。那我们求某一个区间的和可以有一些方法比如:
暴力解法就是遍历所有的区间求每一个区间的和,这个区间的和是区间的数一个一个加起来的;
前缀和解法就是利用不同前缀和的差来确定区间的和,上面的例子就是这种情况 presum[5] - presum[2] = nums[2] + nums[3] + nums[4]。
前缀和+Hash表:
统计以每一个 nums[i] 为结尾,和为 k 的子数组数量即是答案。对于求解以某一个 nums[i] 为结尾的,和为 k 的子数组数量,本质上是求解在[0, i]中,
sum 数组中有多少个值为 sum[i + 1] - k 的数,这可以在遍历过程中使用「哈希表」进行同步记录出现过的前缀和及其次数。
class Solution {
public int subarraySum(int[] nums, int k) {
int len = nums.length, ans = 0;
int[] sum = new int[len + 1];
for (int i = 0; i < len; i++) {
sum[i + 1] = sum[i] + nums[i];
}
HashMap<Integer, Integer> map = new HashMap<>();
map.put(0, 1 );
for (int i = 1; i <= len; i++) {
int t = nums[i], d = t - k;
ans += map.getOrDefault(d, 0);
map.put(t, getOrDefault(t, 0) + 1);
}
return ans;
}
}
1248. 统计「优美子数组」
给你一个整数数组 nums 和一个整数 k。如果某个连续子数组中恰好有 k 个奇数数字,我们就认为这个子数组是「优美子数组」。
请返回这个数组中 「优美子数组」 的数目。
输入:nums = [1,1,2,1,1], k = 3
输出:2
解释:包含 3 个奇数的子数组是 [1,1,2,1] 和 [1,2,1,1] 。
class Solution {
public int numberOfSubarrays(int[] nums, int k) {
int len = nums.length, ans = 0;
int[] odd = new int[len + 1];
// 先分别计算出数组前1, 2, 3 ...个数中奇数存在的个数。
for (int i = 0; i < len; i++) {
odd[i + 1] = odd[i] + (nums[i] & 1);
}
HashMap<Integer, Integer> map = new HashMap<>();
map.put(0, 1);
for (int i = 1; i <= len; i++) {
int t = odd[i], d = t - k;
ans += map.getOrDefault(d, 0);
map.put(t, map.getOrDefault(t, 0) + 1);
}
return ans;
}
}
974. 和可被 K 整除的子数组的个数⭐⭐
给定一个整数数组 nums 和一个整数 k ,返回其中元素之和可被 k 整除的(连续、非空) 子数组 的数目。
子数组 是数组的 连续 部分。
要解决这道题我们要先知道同余定理,同余定理就是对于两个数a和b,其对m取余后结果相同,即说明a与b对m的模相同,这时称,a和b是同余的。
进而,既然a和b同余了,那说明a - b对m的模一定为0,也就是a - b的值可以是m的整数倍。
在做这一题时,提交发现用例 nums = [-1, 2, 9], k = 2 过不了,原因是漏掉了2这种情况。
对于任何同号的两个整数,其取余结果没有争议,所有语言的运算结果都是让商尽可能小;
对于异号的两个整数,C++/Java语言的原则是让商尽可能大,很多新型语言和网页计算器的原则是让商尽可能小。
对于[-1, 2, 9]这个用例其前缀和数组是[0, -1, 1, 10]。在Java语言中-1对2取余是-1,而Python语言是1。而我们发现 1 - (-1) = 2,是2的整数倍。也就是说应该让
-1对2取模等于1才行,这样才不会漏掉2这种情况。我们统一将余数转为正数。
两个前缀和对k的余数相同,那他们的差就是k的整数倍。
class Solution {
public int subarraysDivByK(int[] nums, int k) {
int len = nums.length, ans = 0, carry = 0;
int[] sum = new int[len + 1];
for (int i = 0; i < len; i++) {
sum[i + 1] = sum[i] + nums[i];
}
HashMap<Integer, Integer> map = new HashMap<>();
map.put(0, 1);
for (int i = 1; i <= len; i++) {
carry = ((sum[i] % k) + k) % k;
ans += map.getOrDefault(carry, 0);
map.put(carry, map.getOrDefault(carry, 0) + 1);
}
return ans;
}
}
不用数组来存放前缀和
class Solution {
public int subarraysDivByK(int[] nums, int k) {
int sum = 0, carry = 0, ans = 0;
HashMap<Integer, Integer> map = new HashMap<>();
map.put(0, 1);
for (int num : nums) {
sum += num;
carry = sum % k;
if (carry < 0) {
carry = carry + k;
}
ans += map.getOrDefault(carry, 0);
map.put(carry, map.getOrDefault(carry, 0) + 1);
}
return ans;
}
}
523. 连续的子数组和
给你一个整数数组 nums 和一个整数 k ,编写一个函数来判断该数组是否含有同时满足下述条件的连续子数组:
- 子数组大小 至少为 2 ,且
- 子数组元素总和为 k 的倍数。
如果存在,返回 true ;否则,返回 false 。
如果存在一个整数 n ,令整数 x 符合 x = n * k ,则称 x 是 k 的一个倍数。0 始终视为 k 的一个倍数。
class Solution {
public boolean checkSubarraySum(int[] nums, int k) {
int len = nums.length;
int[] sum = new int[len + 1];
// 先求出前缀和
for (int i = 0; i < len; i++) {
sum[i + 1] = sum[i] + nums[i];
}
Set<Integer> set = new HashSet<>();
// 还是用到了同余定理,两个数对同一个数k的模相同时,这两个数的差对k的模是0,也就是k的倍数。
// 子数组大小至少为2,从i = 2开始遍历处理sum前缀和数组,将前缀和对k的模放入set集合中。
for (int i = 2; i <= len; i++) {
set.add(sum[i - 2] % k);
if (set.contains(sum[i] % k)) {
return true;
}
}
return false;
}
}
525. 连续数组⭐⭐
给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。
解题思路:
首先,我们做一个等价,题目让你找 0 和 1 数量相同的最长子数组,如果我们把 0 视作 -1,就把题目转变成了:寻找和为 0 的最长子数组。
涉及到和为 xxx 的子数组,就是要考察 前缀和技巧 和哈希表的结合使用了。
求和为 0 的最长子数组,相当于让你去 preSum 数组中找 i, j,使得 preSum[i] - preSum[j] == 0,其中 i > j 且 i - j 要尽可能大。
那么我们用一个哈希表 valToIndex 存储前缀和到索引的映射,给定任意 preSum[i]。
我们都能通过 valToIndex 快速判断是否存在 j,使得 preSum[i] - preSum[j] == 0。
值得一提的是,我给的解法中 preSum 数组可以进一步简化成变量,这个优化可以留给你来做。
class Solution {
public int findMaxLength(int[] nums) {
int n = nums.length;
int[] preSum = new int[n + 1];
preSum[0] = 0;
// 计算 nums 的前缀和
for (int i = 0; i < n; i++) {
preSum[i + 1] = preSum[i] + (nums[i] == 0 ? -1 : 1);
}
// 前缀和到索引的映射,方便快速查找所需的前缀和。
HashMap<Integer, Integer> valToIndex = new HashMap<>();
int res = 0;
for (int i = 0; i < preSum.length; i++) {
// 如果这个前缀和还没有对应的索引,说明这个前缀和第一次出现,记录下来。
if (!valToIndex.containsKey(preSum[i])) {
valToIndex.put(preSum[i], i);
} else {
// 这个前缀和已经出现过了,则找到一个和为 0 的子数组。
res = Math.max(res, i - valToIndex.get(preSum[i]));
}
// 因为题目想找长度最大的子数组,所以前缀和索引应尽可能小。
}
return res;
}
}
1124. 表现良好的最长时间段⭐⭐
给你一份工作时间表 hours,上面记录着某一位员工每天的工作小时数。
我们认为当员工一天中的工作小时数大于 8 小时的时候,那么这一天就是「劳累的一天」。
所谓「表现良好的时间段」,意味在这段时间内,「劳累的天数」是严格 大于「不劳累的天数」。
请你返回「表现良好时间段」的最大长度。
解题思路:
题目说 hours[i] 以 8 作为分界线,那么我们就要条件反射地想到对数据进行「归一化」处理,比如把所有大于 8 的元素视为 +1,把所有小于 8 的元素视为 -1,
这样一来,这道题就改造成了:计算数组中元素和大于 0 的子数组的最大长度。
然后回想之前子数组相关的题目,第 525. 连续数组 是问和为 0 的子数组,974. 和可被 K 整除的子数组 是问和能被 k 整除的子数组,这道题和它们很类似,都是
考察前缀和 + 哈希表的组合场景。
我们借助哈希表存储前缀和到索引的映射,这样就能快速寻找一个 j 使得 preSum[i] - preSum[j] > 0 了,具体看代码注释吧。
值得一提的是,我给的解法中 preSum 数组可以进一步简化成变量,这个优化可以留给你来做。
class Solution {
public int longestWPI(int[] hours) {
int n = hours.length;
int[] preSum = new int[n + 1];
preSum[0] = 0;
// 前缀和到索引的映射,方便快速查找所需的前缀和
HashMap<Integer, Integer> valToIndex = new HashMap<>();
int res = 0;
for (int i = 1; i <= n; i++) {
// 计算 nums[0..i-1] 的前缀和
preSum[i] = preSum[i - 1] + (hours[i - 1] > 8 ? 1 : -1);
// 如果这个前缀和还没有对应的索引,说明这个前缀和第一次出现,记录下来。
if (!valToIndex.containsKey(preSum[i])) {
valToIndex.put(preSum[i], i);
} else {
// 因为题目想找长度最大的子数组,valToIndex 中的索引应尽可能小。
// 所以这里什么都不做。
}
// 现在我们想找 hours[0..i-1] 中元素和大于 0 的子数组。
// 这就要根据 preSum[i] 的正负分情况讨论了。
if (preSum[i] > 0) {
// preSum[i] 为正,说明 hours[0..i-1] 都是「表现良好的时间段」。
res = Math.max(res, i);
} else {
// preSum[i] 为负,需要寻找一个 j 使得 preSum[i] - preSum[j] > 0。
// 且 j 应该尽可能小,即寻找 preSum[j] == preSum[i] - 1。
if (valToIndex.containsKey(preSum[i] - 1)) {
int j = valToIndex.get(preSum[i] - 1);
res = Math.max(res, i - j);
}
}
}
return res;
}
}
1352. 最后 K 个数的乘积
请你实现一个「数字乘积类」ProductOfNumbers,要求支持下述两种方法:
- add(int num)
- 将数字 num 添加到当前数字列表的最后面。
- getProduct(int k)
- 返回当前数字列表中,最后 k 个数字的乘积;
- 你可以假设当前列表中始终 至少 包含 k 个数字。
题目数据保证:任何时候,任一连续数字序列的乘积都在 32-bit 整数范围内,不会溢出。
class ProductOfNumbers {
// 前缀积数组
// preProduct[i] / preProduct[j] 就是 [i, j] 之间的元素积
ArrayList<Integer> preProduct = new ArrayList<>();
public ProductOfNumbers() {
// 初始化放一个 1,便于计算后续添加元素的乘积
preProduct.add(1);
}
public void add(int num) {
if (num == 0) {
// 如果添加的元素是 0,则前面的元素积都废了
preProduct.clear();
preProduct.add(1);
return;
}
int n = preProduct.size();
// 前缀积数组中每个元素
preProduct.add(preProduct.get(n - 1) * num);
}
public int getProduct(int k) {
int n = preProduct.size();
if (k > n - 1) {
// 不足 k 个元素,是因为最后 k 个元素存在 0
return 0;
}
// 计算最后 k 个元素积
return preProduct.get(n - 1) / preProduct.get(n - k - 1);
}
}
1310. 子数组异或查询
有一个正整数数组 arr,现给你一个对应的查询数组 queries,其中 queries[i] = [Li, Ri]。
对于每个查询 i,请你计算从 Li 到 Ri 的 XOR 值(即 arr[Li] xor arr[Li+1] xor ... xor arr[Ri])作为本次查询的结果。
并返回一个包含给定查询 queries 所有结果的数组。
class Solution {
public int[] xorQueries(int[] arr, int[][] queries) {
int[] preSum = new int[arr.length + 1];
for (int i = 1; i < preSum.length; i++) {
preSum[i] = preSum[i - 1] ^ arr[i - 1];
}
int[] ans = new int[queries.length];
for (int i = 0; i < queries.length; i++) {
int[] query = queries[i];
ans[i] = preSum[query[1] + 1] ^ preSum[query[0]];
}
return ans;
}
}
差分数组
前缀和思想非常类似的算法技巧「差分数组」,差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减。
比如说,我给你输入一个数组 nums,然后又要求给区间 nums[2..6] 全部加 1,再给 nums[3..9] 全部减 3,再给 nums[0..4] 全部加 2,再给…
一通操作猛如虎,然后问你,最后 nums 数组的值是什么?
常规的思路很容易,你让我给区间 nums[i..j] 加上 val,那我就一个 for 循环给它们都加上呗,还能咋样?这种思路的时间复杂度是 O(N),由于这个场景下对
nums 的修改非常频繁,所以效率会很低下。
这里就需要差分数组的技巧,类似前缀和技巧构造的 prefix 数组。
我们先对 nums 数组构造一个 diff 差分数组,diff[i] 就是 nums[i] 和 nums[i-1] 之差:
int[] diff = new int[nums.length];
// 构造差分数组
diff[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
diff[i] = nums[i] - nums[i - 1];
}

通过这个 diff 差分数组是可以反推出原始数组 nums 的,代码逻辑如下:
int[] res = new int[diff.length];
// 根据差分数组构造结果数组
res[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
res[i] = res[i - 1] + diff[i];
}
这样构造差分数组 diff,就可以快速进行区间增减的操作。
如果你想对区间 nums[i..j] 的元素全部加 3,那么只需要让 diff[i] += 3,然后再让 diff[j+1] -= 3 即可:

原理很简单,回想 diff 数组反推 nums 数组的过程,diff[i] += 3 意味着给 nums[i..] 所有的元素都加了 3,然后 diff[j+1] -= 3 又意味着对于 nums[j+1..] 所有元素
再减 3,那综合起来,是不是就是对 nums[i..j] 中的所有元素都加 3了?
只要花费 O(1) 的时间修改 diff 数组,就相当于给 nums 的整个区间做了修改。多次修改 diff,然后通过 diff 数组反推,即可得到 nums 修改后的结果。
现在我们把差分数组抽象成一个类,包含 increment 方法和 result 方法:
// 差分数组工具类
class Difference {
// 差分数组
private int[] diff;
/* 输入一个初始数组,区间操作将在这个数组上进行 */
public Difference(int[] nums) {
assert nums.length > 0;
diff = new int[nums.length];
// 根据初始数组构造差分数组
diff[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
diff[i] = nums[i] - nums[i - 1];
}
}
/* 给闭区间 [i, j] 增加 val(可以是负数)*/
public void increment(int i, int j, int val) {
diff[i] += val;
if (j + 1 < diff.length) {
diff[j + 1] -= val;
}
}
/* 返回结果数组 */
public int[] result() {
int[] res = new int[diff.length];
// 根据差分数组构造结果数组
res[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
res[i] = res[i - 1] + diff[i];
}
return res;
}
}
这里注意一下 increment 方法中的 if 语句:
public void increment(int i, int j, int val) {
diff[i] += val;
if (j + 1 < diff.length) {
diff[j + 1] -= val;
}
}
当 j+1 >= diff.length 时,说明是对 nums[i] 及以后的整个数组都进行修改,那么就不需要再给 diff 数组减 val 了。
370.区间加法

class Solution {
int[] getModifiedArray(int length, int[][] updates) {
int[] nums = new int[length];
Difference df = new Difference(nums);
for (int[] update : updates) {
int i = update[0];
int j = update[1];
int val = update[2];
df.increment(i, j, val);
}
return df.result();
}
}
// 差分数组工具类
class Difference {
// 差分数组
private int[] diff;
/* 输入一个初始数组,区间操作将在这个数组上进行 */
public Difference(int[] nums) {
assert nums.length > 0;
diff = new int[nums.length];
// 根据初始数组构造差分数组
diff[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
diff[i] = nums[i] - nums[i - 1];
}
}
/* 给闭区间 [i, j] 增加 val(可以是负数)*/
public void increment(int i, int j, int val) {
diff[i] += val;
if (j + 1 < diff.length) {
diff[j + 1] -= val;
}
}
/* 返回结果数组 */
public int[] result() {
int[] res = new int[diff.length];
// 根据差分数组构造结果数组
res[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
res[i] = res[i - 1] + diff[i];
}
return res;
}
}
1109. 航班预订统计
这里有 n 个航班,它们分别从 1 到 n 进行编号。
有一份航班预订表 bookings ,表中第 i 条预订记录 bookings[i] = [firsti, lasti, seatsi] 意味着在从 firsti 到 lasti (包含 firsti 和 lasti )
的 每个航班 上预订了 seatsi 个座位。
请你返回一个长度为 n 的数组 answer,里面的元素是每个航班预定的座位总数。
class Solution {
public int[] corpFlightBookings(int[][] bookings, int n) {
int[] answer = new int[n + 1];
Difference diff = new Difference(answer);
for (int[] update : bookings) {
int i = update[0];
int j = update[1];
int val = update[2];
diff.increment(i, j, val);
}
int[] temp = diff.result();
int[] res = new int[n];
for (int i = 0; i < n; i++) {
res[i] = temp[i + 1];
}
return res;
}
}
class Difference {
int[] diff;
public Difference(int[] nums) {
diff = new int[nums.length];
diff[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
diff[i] = nums[i] - nums[i - 1];
}
}
public void increment(int i, int j, int val) {
diff[i] += val;
if (j + 1 < diff.length) {
diff[j + 1] -= val;
}
}
public int[] result() {
int[] res = new int[diff.length];
res[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
res[i] = res[i - 1] + diff[i];
}
return res;
}
}
1094. 拼车
车上最初有 capacity 个空座位。车 只能 向一个方向行驶(也就是说,不允许掉头或改变方向)
给定整数 capacity 和一个数组 trips , trip[i] = [numPassengersi, fromi, toi] 表示第 i 次旅行有 numPassengersi 乘客,接他们和放他们的位置分
别是 fromi 和 toi 。这些位置是从汽车的初始位置向东的公里数。
当且仅当你可以在所有给定的行程中接送所有乘客时,返回 true,否则请返回 false。
class Solution {
boolean carPooling(int[][] trips, int capacity) {
// 最多有 1001 个车站
int[] nums = new int[1001];
// 构造差分解法
Difference df = new Difference(nums);
for (int[] trip : trips) {
// 乘客数量
int val = trip[0];
// 第 trip[1] 站乘客上车
int i = trip[1];
// 第 trip[2] 站乘客已经下车,
// 即乘客在车上的区间是 [trip[1], trip[2] - 1]
int j = trip[2] - 1;
// 进行区间操作
df.increment(i, j, val);
}
int[] res = df.result();
// 客车自始至终都不应该超载
for (int i = 0; i < res.length; i++) {
if (capacity < res[i]) {
return false;
}
}
return true;
}
}
// 差分数组工具类
class Difference {
// 差分数组
private int[] diff;
/* 输入一个初始数组,区间操作将在这个数组上进行 */
public Difference(int[] nums) {
assert nums.length > 0;
diff = new int[nums.length];
// 根据初始数组构造差分数组
diff[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
diff[i] = nums[i] - nums[i - 1];
}
}
/* 给闭区间 [i, j] 增加 val(可以是负数)*/
public void increment(int i, int j, int val) {
diff[i] += val;
if (j + 1 < diff.length) {
diff[j + 1] -= val;
}
}
/* 返回结果数组 */
public int[] result() {
int[] res = new int[diff.length];
// 根据差分数组构造结果数组
res[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
res[i] = res[i - 1] + diff[i];
}
return res;
}
}
253. 会议室 II
给你一个会议时间安排的数组 intervals ,每个会议时间都会包括开始和结束的时间 intervals[i] = [starti, endi] ,返回 所需会议室的最小数量 。
示例 1:
输入:intervals = [[0,30],[5,10],[15,20]]
输出:2示例 2:
输入:intervals = [[7,10],[2,4]]
输出:1
class Solution {
public int minMeetingRooms(int[][] intervals) {
int maxLen = 0;
int n = intervals[0].length;
for (int i = 0; i < intervals.length; i++) {
for (int j = 0; j < intervals[0].length; j++) {
maxLen = Math.max(maxLen, intervals[i][j]);
}
}
int[] nums = new int[maxLen];
Difference diff = new Difference(nums);
for (int[] interval : intervals) {
int i = interval[0];
int j = interval[1] - 1;
diff.increment(i, j, 1);
}
int[] res = diff.result();
int max = Integer.MIN_VALUE;
for (int num : res) {
max = Math.max(max, num);
}
return max;
}
}
class Difference {
private int[] diff;
public Difference(int[] nums) {
diff = new int[nums.length];
diff[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
diff[i] = nums[i] - nums[i - 1];
}
}
public void increment(int i, int j, int val) {
diff[i] += val;
if (j + 1 < diff.length) {
diff[j + 1] -= val;
}
}
public int[] result() {
int[] res = new int[diff.length];
res[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
res[i] = res[i - 1] + diff[i];
}
return res;
}
}
求和
2. 两数相加⭐⭐⭐
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
复杂版:
class Solution {
List<ListNode> list1 = new ArrayList<>();
List<ListNode> list2 = new ArrayList<>();
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
traverse(l1, list1);
traverse(l2, list2);
int m = list1.size() - 1;
int n = list2.size() - 1;
ListNode dummy = new ListNode(-1);
int carry = 0;
while (m >= 0 || n >= 0 || carry != 0) {
int digitA = m >= 0 ? list1.get(m).val : 0;
int digitB = n >= 0 ? list2.get(n).val : 0;
int sum = digitA + digitB + carry;
carry = sum >= 10 ? 1 : 0;
sum = sum >= 10 ? sum - 10 : sum;
ListNode node = new ListNode(sum);
node.next = dummy.next;
dummy.next = node;
m--;
n--;
}
return reverse(dummy.next);
}
// 倒序遍历单链表
private void traverse(ListNode root, List<ListNode> list) {
if (root == null) {
return;
}
traverse(root.next, list);
list.add(root);
}
// 翻转单链表
private ListNode reverse(ListNode root) {
if (root == null || root.next == null) {
return root;
}
ListNode last = reverse(root.next);
root.next.next = root;
root.next = null;
return last;
}
}
简单版:
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode dummy = new ListNode(-1);
ListNode cur = dummy;
int carry = 0;
while (l1 != null || l2 != null || carry != 0) {
int l1Val = l1 != null ? l1.val : 0;
int l2Val = l2 != null ? l2.val : 0;
int sum = l1Val + l2Val + carry;
carry = sum >= 10 ? 1 : 0;
sum = sum >= 10 ? sum - 10 : sum;
ListNode sumNode = new ListNode(sum);
cur.next = sumNode;
cur = sumNode;
if (l1 != null) {
l1 = l1.next;
}
if (l2 != null) {
l2 = l2.next;
}
}
return dummy.next;
}
}
67. 二进制求和
给你两个二进制字符串,返回它们的和(用二进制表示)。
输入为 非空 字符串且只包含数字 1 和 0。
输入: a = "11", b = "1"
输出: "100"
https://leetcode.cn/problems/add-binary/solution/fu-xue-ming-zhu-qiu-jia-fa-ti-mu-kan-zhe-h4kx/
需要注意的点:
- 不可以把字符串表示的「加数」先转化成 int 型数字再求和,因为可能溢出;
- 两个「加数」的字符串长度可能不同;
- 在最后,如果进位 carry 不为 0,那么最后需要计算进位;
- 注意结果数字是否为低位结果在前,根据题目要求判断最后是否要反转结果。
代码说明:
-
while (i >= 0 || j >= 0 || carry != 0)含义是字符串 num 和数字 k 只要有一个没遍历完,那么就继续遍历;
-
如果字符串 num 和数字 k 都遍历完了,但是最后留下的进位 carry != 0,那么需要把进位也保留到结果中;
-
取 digit 的时候,如果字符串 a 和 b 中有一个已经遍历完了(即 i <= 0 或者 j <= 0),则认为 a 和 b 的对应位置是 0。

class Solution {
public String addBinary(String a, String b) {
StringBuilder res = new StringBuilder(); // 返回结果
int i = a.length() - 1; // 标记遍历到 a 的位置
int j = b.length() - 1; // 标记遍历到 b 的位置
int carry = 0; // 进位
while (i >= 0 || j >= 0 || carry != 0) { // a 没遍历完,或 b 没遍历完,或进位不为0
int digitA = i >= 0 ? a.charAt(i) - '0' : 0; // 当前 a 的取值
int digitB = j >= 0 ? b.charAt(j) - '0' : 0; // 当前 b 的取值
int sum = digitA + digitB + carry; // 当前位置相加的结果
carry = sum >= 2 ? 1 : 0; // 是否有进位
sum = sum >= 2 ? sum - 2 : sum; // 去除进位后留下的数字
res.append(sum); // 把去除进位后留下的数字拼接到结果中
i--; // 遍历到 a 的位置向左移动
j--; // 遍历到 b 的位置向左移动
}
return res.reverse().toString(); // 把结果反转并返回
}
}
「加法」系列题目都不难,其实就是 「列竖式」模拟法。
需要注意的是 while循环结束条件,注意遍历两个「加数」不要越界,以及进位。
43. 字符串相乘⭐⭐⭐
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
注意:不能使用任何内置的 BigInteger 库或直接将输入转换为整数。
参考题解:https://labuladong.gitee.io/algo/4/33/127/
class Solution {
public String multiply(String num1, String num2) {
int m = num1.length(), n = num2.length();
// 结果最多为 m + n 位数
int[] res = new int[m + n];
// 从个位数开始逐位相乘
for (int i = m - 1; i >= 0; i--) {
for (int j = n - 1; j >= 0; j--) {
int mul = (num1.charAt(i) - '0') * (num2.charAt(j) - '0');
// 乘积在 res 对应的索引位置
int p1 = i + j, p2 = i + j + 1;
// 叠加到 res 上
int sum = mul + res[p2];
res[p2] = sum % 10;
res[p1] += sum / 10;
}
}
// 结果前缀可能存的 0(未使用的位)
int i = 0;
while (i < res.length && res[i] == 0) {
i++;
}
// 将计算结果转化成字符串
StringBuilder sb = new StringBuilder();
for (; i < res.length; i++) {
sb.append(res[i]);
}
return sb.length() == 0 ? "0" : sb.toString();
}
}
415. 字符串相加
给定两个字符串形式的非负整数 num1 和num2 ,计算它们的和并同样以字符串形式返回。
你不能使用任何內建的用于处理大整数的库(比如 BigInteger), 也不能直接将输入的字符串转换为整数形式。
class Solution {
public String addStrings(String num1, String num2) {
StringBuilder res = new StringBuilder();
int i = num1.length() - 1;
int j = num2.length() - 1;
int carry = 0;
while (i >= 0 || j >= 0 || carry != 0) {
int digitA = i >= 0 ? num1.charAt(i) - '0' : 0;
int digitB = j >= 0 ? num2.charAt(j) - '0' : 0;
int sum = digitA + digitB + carry;
// 进位carry
carry = sum >= 10 ? 1 : 0;
sum = sum >= 10 ? sum - 10 : sum;
res.append(sum);
i--;
j--;
}
return res.reverse().toString();
}
}
989. 数组形式的整数加法
整数的 数组形式 num 是按照从左到右的顺序表示其数字的数组。
例如,对于 num = 1321 ,数组形式是 [1,3,2,1] 。
给定 num ,整数的 数组形式 ,和整数 k ,返回 整数 num + k 的 数组形式 。
输入:num = [1,2,0,0], k = 34
输出:[1,2,3,4]
解释:1200 + 34 = 1234
class Solution {
public List<Integer> addToArrayForm(int[] num, int k) {
StringBuilder res = new StringBuilder();
// 把int类型的k转为字符串
String str = k + "";
char[] chars = str.toCharArray();
int i = num.length - 1;
int j = chars.length - 1;
int carry = 0;
while (i >= 0 || j >= 0 || carry != 0) {
int digitA = i >= 0 ? num[i] : 0;
int digitB = j >= 0 ? chars[j] - '0' : 0;
int sum = digitA + digitB + carry;
carry = sum >= 10 ? 1 : 0;
sum = sum >= 10 ? sum - 10 : sum;
res.append(sum);
i--;
j--;
}
String s = res.reverse().toString();
List<Integer> list = new ArrayList<>();
for (char ch : s.toCharArray()) {
list.add(ch - '0');
}
return list;
}
}
445. 两数相加 II
给你两个 非空 链表来代表两个非负整数。数字最高位位于链表开始位置。它们的每个节点只存储一位数字。将这两数相加会返回一个新的链表。
你可以假设除了数字 0 之外,这两个数字都不会以零开头。
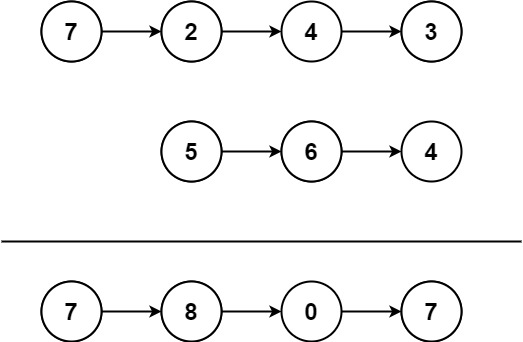
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
List<ListNode> list1 = new ArrayList<>();
List<ListNode> list2 = new ArrayList<>();
ListNode dummy = new ListNode(-1);
while (l1 != null) {
list1.add(l1);
l1 = l1.next;
}
while (l2 != null) {
list2.add(l2);
l2 = l2.next;
}
int m = list1.size() - 1;
int n = list2.size() - 1;
int carry = 0;
while (m >= 0 || n >= 0 || carry != 0) {
int digitA = m >= 0 ? list1.get(m).val : 0;
int digitB = n >= 0 ? list2.get(n).val : 0;
int sum = digitA + digitB + carry;
carry = sum >= 10 ? 1 : 0;
sum = sum >= 10 ? sum - 10 : sum;
ListNode node = new ListNode(sum);
node.next = dummy.next;
dummy.next = node;
m--;
n--;
}
return dummy.next;
}
}
链表
21. 合并两个有序链表⭐
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
class Solution {
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
ListNode dummyHead = new ListNode(0);
ListNode last = dummyHead;
while (list1 != null && list2 != null) {
if (list1.val <= list2.val) {
last.next = list1;
list1 = list1.next;
} else {
last.next = list2;
list2 = list2.next;
}
last = last.next;
}
if (list1 != null) {
last.next = list1;
}
if (list2 != null) {
last.next = list2;
}
return dummyHead.next;
}
}
206. 反转链表⭐⭐⭐
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
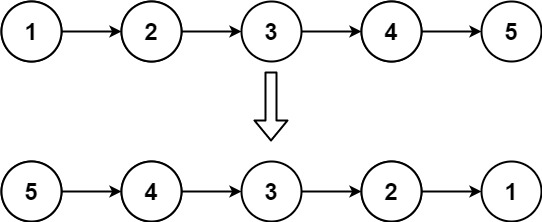
反转单链表迭代实现:
class Solution {
// 链表反转之后,原来的第一个节点就要指向null
// 我们对原始链表一个节点,一个节点的进行反转
// 首先将当前正在进行反转的下一个节点保存下来,然后改变反转节点的指向,指向prev指向的节点
// 然后将prev指向cur,将cur指向下一个节点,代表马上处理这个节点。
public ListNode reverseList(ListNode head) {
ListNode prev = null;
ListNode cur = head;
while (cur != null) {
ListNode nextNode = cur.next;
cur.next = prev;
prev = cur;
cur = nextNode;
}
// 当 cur == null 时,此时prev就是新的链表头
return prev;
}
}
反转单链表递归实现:
class Solution {
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
// 找到链表尾部的last之后一直返回。
ListNode last = reverseList(head.next);
head.next.next = head;
head.next = null;
return last;
}
}
看起来是不是感觉不知所云,完全不能理解这样为什么能够反转链表?这就对了,这个算法常常拿来显示递归的巧妙和优美,我们下面来详细解释一下这段代码。
对于递归算法,最重要的就是明确递归函数的定义。具体来说,我们的 reverse 函数定义是这样的:
输入一个节点 head,将「以 head 为起点」的链表反转,并返回反转之后的头结点。
明白了函数的定义,再来看这个问题。比如说我们想反转这个链表:

那么输入 reverse(head) 后,会在这里进行递归:
ListNode last = reverse(head.next);
不要跳进递归(你的脑袋能压几个栈呀?),而是要根据刚才的函数定义,来弄清楚这段代码会产生什么结果:

这个 reverse(head.next) 执行完成后,整个链表就成了这样:

并且根据函数定义,reverse 函数会返回反转之后的头结点,我们用变量 last 接收了。
现在再来看下面的代码:
head.next.next = head;

接下来:
head.next = null;
return last;

神不神奇,这样整个链表就反转过来了!递归代码就是这么简洁优雅,不过其中有两个地方需要注意:
1、递归函数要有 base case,也就是这句:
if (head == null || head.next == null) {
return head;
}
意思是如果链表为空或者只有一个节点的时候,反转结果就是它自己,直接返回即可。
2、当链表递归反转之后,新的头结点是 last,而之前的 head 变成了最后一个节点,别忘了链表的末尾要指向 null:
head.next = null;
理解了这两点后,我们就可以进一步深入了,接下来的问题其实都是在这个算法上的扩展。
反转链表前N个节点
这次我们实现一个这样的函数:
// 将链表的前 n 个节点反转(n <= 链表长度)
ListNode reverseN(ListNode head, int n)
比如说对于下图链表,执行 reverseN(head, 3):

解决思路和反转整个链表差不多,只要稍加修改即可:
ListNode successor = null; // 后驱节点
// 反转以 head 为起点的 n 个节点,返回新的头结点
ListNode reverseN(ListNode head, int n) {
if (n == 1) {
// 记录第 n + 1 个节点
successor = head.next;
return head;
}
// 以 head.next 为起点,需要反转前 n - 1 个节点
ListNode last = reverseN(head.next, n - 1);
head.next.next = head;
// 让反转之后的 head 节点和后面的节点连起来
head.next = successor;
return last;
}
具体的区别:
1、base case 变为 n == 1,反转一个元素,就是它本身,同时要记录后驱节点。
2、刚才我们直接把 head.next 设置为 null,因为整个链表反转后原来的 head 变成了整个链表的最后一个节点。但现在 head 节点在递归反转之后不一定是最
后一个节点了,所以要记录后驱 successor(第 n + 1 个节点),反转之后将 head 连接上。

OK,如果这个函数你也能看懂,就离实现「反转一部分链表」不远了。
反转链表的一部分
现在解决我们最开始提出的问题,给一个索引区间 [m, n](索引从 1 开始),仅仅反转区间中的链表元素。
ListNode reverseBetween(ListNode head, int m, int n)
首先,如果 m == 1,就相当于反转链表开头的 n 个元素嘛,也就是我们刚才实现的功能:
ListNode reverseBetween(ListNode head, int m, int n) {
// base case
if (m == 1) {
// 相当于反转前 n 个元素
return reverseN(head, n);
}
// ...
}
如果 m != 1 怎么办?如果我们把 head 的索引视为 1,那么我们是想从第 m 个元素开始反转对吧。
如果把 head.next 的索引视为 1 呢?那么相对于 head.next,反转的区间应该是从第 m - 1 个元素开始的;那么对于 head.next.next 呢……
区别于迭代思想,这就是递归思想,所以我们可以完成代码:
ListNode reverseBetween(ListNode head, int m, int n) {
// base case
if (m == 1) {
// 秒啊
return reverseN(head, n);
}
// 前进到反转的起点触发 base case
head.next = reverseBetween(head.next, m - 1, n - 1);
return head;
}
递归的思想相对迭代思想,稍微有点难以理解,处理的技巧是:不要跳进递归,而是利用明确的定义来实现算法逻辑,当成黑盒子来使用。
处理看起来比较困难的问题,可以尝试化整为零,把一些简单的解法进行修改,解决困难的问题。
值得一提的是,递归操作链表并不高效。和迭代解法相比,虽然时间复杂度都是 O(N),但是迭代解法的空间复杂度是 O(1),而递归解法需要堆栈,空间复杂度是
O(N)。所以递归操作链表可以作为对递归算法的练习或者拿去和小伙伴装逼,但是考虑效率的话还是使用迭代算法更好。
92. 反转链表 II
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
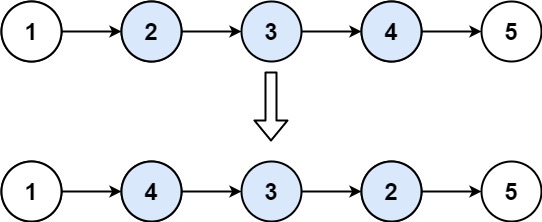
输入:head = [1,2,3,4,5], left = 2, right = 4
输出:[1,4,3,2,5]
迭代实现:
class Solution {
public ListNode reverseBetween(ListNode head, int left, int right) {
ListNode dummy = new ListNode(-1, head);
ListNode cur = dummy;
ListNode pre;
ListNode prev = null;
int step = 0;
ListNode startDummy = new ListNode(-1);
ListNode endDummy = new ListNode(-1);
while (cur != null) {
pre = cur;
cur = cur.next;
step++;
if (step == left) {
startDummy.next = cur;
prev = pre;
}
if (step == right) {
endDummy.next = cur;
break;
}
}
ListNode second = cur.next;
// 断链
cur.next = null;
ListNode node = reverseList(startDummy.next);
prev.next = node;
while (node.next != null) {
node = node.next;
}
node.next = second;
return dummy.next;
}
public ListNode reverseList(ListNode head) {
ListNode prev = null;
ListNode cur = head;
while (cur != null) {
ListNode nextNode = cur.next;
cur.next = prev;
prev = cur;
cur = nextNode;
}
return prev;
}
}
递归实现:
class Solution {
public ListNode reverseBetween(ListNode head, int left, int right) {
// base case
if (left == 1) {
return reverseN(head, right);
}
head.next = reverseBetween(head.next, left - 1, right - 1);
return head;
}
ListNode successor = null;
// 反转前n个节点
private ListNode reverseN(ListNode head, int n) {
if (n == 1) {
successor = head.next;
return head;
}
ListNode last = reverseN(head.next, n - 1);
head.next.next = head;
head.next = successor;
return last;
}
}
24. 两两交换链表中的节点⭐
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
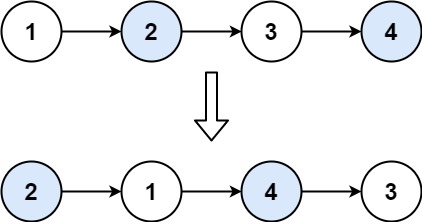
class Solution {
public ListNode swapPairs(ListNode head) {
if (head == null) {
return null;
}
// 构造一个虚拟头节点,统一代码逻辑。
ListNode dummy = new ListNode(0);
// 让虚拟头节点的next指针域指向真正的头节点
dummy.next = head;
// prev首先指向dummy节点
ListNode prev = dummy;
// 确保要交换的两个节点不为null
while (head != null && head.next != null) {
ListNode temp = head.next.next;
prev.next = head.next;
head.next.next = head;
head.next = temp;
prev = head;
head = head.next;
}
return dummy.next;
}
}
感觉链表的题很多都要加入dummyHead来统一代码逻辑。
25. K 个一组翻转链表⭐⭐⭐⭐
给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。
k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
解题思路:
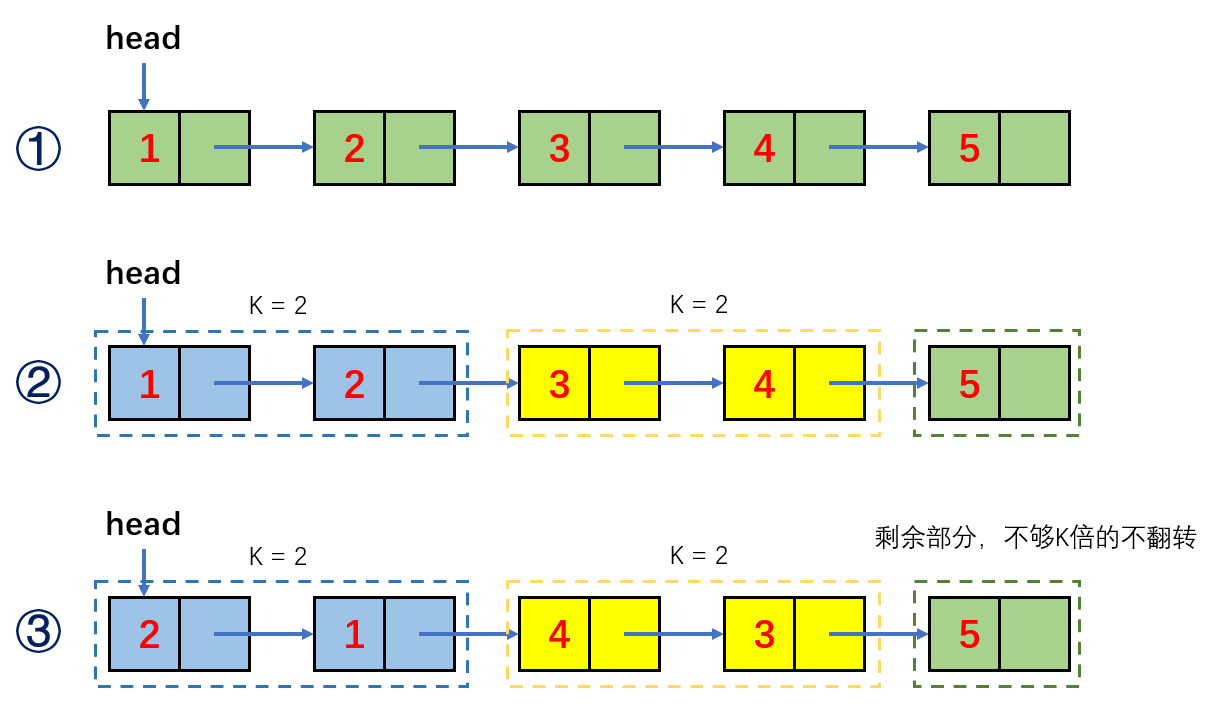
最简单的方法就是以每K个节点为一组,分别进行翻转,将反转的结果追加在新的链表中返回。



到此,K的整数倍个节点都遍历完了,那么剩下的不够整数倍的节点怎么处理?判断循环结束的条件又是什么呢?
显然是当end指针为空,且start指向的这组节点数量不是K个的时候,循环条件结束。

下一步就是直接将pre的指针指向start就可以啦!
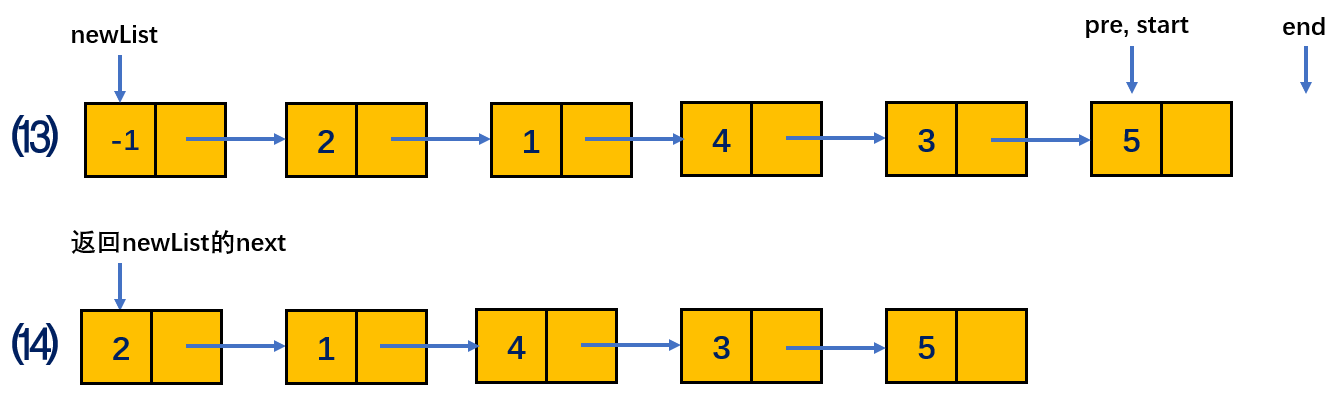
迭代实现:
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
ListNode newList = new ListNode(0);
// newList为新的链表头部
ListNode pre = newList;
ListNode start = head;
ListNode end = head;
// end == null 时退出
while (end != null) {
int count = 0;
while (end != null && count < k - 1) { // 当 count == k - 1时找到了一组k个元素
end = end.next;
count++;
}
// 不满足while循环有两种可能一种是count == k - 1找到了一组k个元素,另一种情况是剩余节点不足k个end == null。
// 来到这里说明剩下的节点不足k个,直接与前面的链表链接起来。
if (end == null) {
pre.next = start;
} else {
// 先把下一个k组的头节点保存一下
ListNode nextStart = end.next;
// 先断开链表,反转链表时才不会出错
end.next = null;
pre.next = reverse(start);
// 让pre最终指向当前反转那一组的最后一个节点
while (pre.next != null) {
pre = pre.next;
}
start = nextStart;
end = nextStart;
}
}
return newList.next;
}
// 反转链表迭代实现
private ListNode reverse(ListNode start) {
ListNode prev = null;
ListNode cur = start;
while (cur != null) {
ListNode temp = cur.next;
cur.next = prev;
prev = cur;
cur = temp;
}
return prev;
}
// 反转链表递归实现
private ListNode reverse(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode last = reverse(head.next);
head.next.next = head;
head.next = null;
return last;
}
}
递归实现:
class Solution {
ListNode reverseKGroup(ListNode head, int k) {
if (head == null) {
return null;
}
// 区间 [a, b) 包含 k 个待反转元素
ListNode a, b;
a = b = head;
for (int i = 0; i < k; i++) {
// 不足 k 个,不需要反转,base case
if (b == null) {
return head;
}
b = b.next;
}
// 反转前 k 个元素
ListNode newHead = reverse(a, k);
// 递归反转后续链表并连接起来
a.next = reverseKGroup(b, k);
return newHead;
}
ListNode successor = null;
ListNode reverse(ListNode head, int k) {
if (k == 1) {
successor = head.next;
return head;
}
ListNode last = reverse(head.next, k - 1);
head.next.next = head;
head.next = successor;
return last;
}
}
61. 旋转链表⭐
给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。
说是循环旋转,但其实本质上是将尾部向前数第K个元素作为头,原来的头接到原来的尾上。
但是注意一点k的值可能会超过链表总节点元素,那么让k对链表总节点数取模,得到要移动的次数。
class Solution {
public ListNode rotateRight(ListNode head, int k) {
// 当链表没有节点或只有一个节点时,直接返回head就行。
if (head == null || head.next == null) {
return head;
}
// 构造哑节点
ListNode dummy = new ListNode(-1, head);
ListNode fast = dummy;
ListNode slow = dummy;
ListNode cur = head;
// 求出链表的总节点个数
int count = 0;
while (cur != null) {
cur = cur.next;
count++;
}
// 确定k的值
k = k % count;
// 让快指针先走k步
while (k > 0) {
k--;
fast = fast.next;
}
// 这里要注意一点,因为我们要将原来链表的尾节点,接上原来的头节点。
// 所以这里fast.next == null时,fast正好指向尾节点,slow.next就是倒数第k个节点,也就是新的头节点。
while (fast.next != null) {
fast = fast.next;
slow = slow.next;
}
// 原来的尾节点指向原来的head节点
fast.next = head;
// slow.next作为新的head节点
head = slow.next;
// 新head节点前面断开,避免成环。
slow.next = null;
return head;
}
}
83. 删除排序链表中的重复元素
给定一个已排序的链表的头 head, 删除所有重复的元素,使每个元素只出现一次。返回 已排序的链表。
class Solution {
public ListNode deleteDuplicates(ListNode head) {
ListNode cur = head;
while (cur.next != null) {
if (cur.val == cur.next.val) {
cur.next = cur.next.next;
} else {
cur = cur.next;
}
}
return head;
}
}
82. 删除排序链表中的重复元素 II⭐
给定一个已排序的链表的头head , 删除原始链表中所有重复数字的节点,只留下不同的数字。返回已排序的链表。
几乎所有的链表题目,都具有相似的解题思路。
建一个「虚拟头节点」dummy 以减少边界判断,往后的答案链表会接在 dummy 后面。
使用 tail 代表当前有效链表的结尾。
通过原输入的 head 指针进行链表扫描。
我们会确保「进入外层循环时 head 不会与上一节点相同」,因此插入时机:
- head 已经没有下一个节点,head 可以被插入;
- head 有一下个节点,但是值与 head 不相同,head 可以被插入。
第一版代码:
class Solution {
public ListNode deleteDuplicates(ListNode head) {
ListNode dummy = new ListNode(-1);
dummy.next = head;
ListNode tail = dummy;
while (head != null) {
if (head.next == null) {
tail.next = head;
tail = head;
}
if (head.next != null && head.val != head.next.val) {
tail.next = head;
tail = head;
}
while (head.next != null && head.val == head.next.val) {
head.next = head.next.next;
}
head = head.next;
}
}
}
优化之后的代码:
class Solution {
public ListNode deleteDuplicates(ListNode head) {
ListNode dummy = new ListNode(-1);
ListNode tail = dummy;
while (head != null) {
// 进入循环时,确保了head不会与上一节点相同
if (head.next == null || head.val != head.next.val) {
tail.next = head;
tail = head;
}
// 如果head与下一节点相同,跳过相同节点
while (head.next != null && head.val == head.next.val) {
head.next = head.next.next;
}
// 来到这里只剩下一个重复的
head = head.next;
}
tail.next = null;
return dummy.next;
}
}
142. 环形链表 II⭐⭐⭐
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链
表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
class Solution {
public ListNode detectCycle(ListNode head) {
ListNode slow = head;
ListNode fast = head;
// 快慢指针先判断链表中是否有环
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
if (slow == fast) { // 有环
ListNode index1 = fast;
ListNode index2 = head;
// 两个指针,从头结点和相遇结点,每次各走一步,直到相遇,相遇点即为环入口。
while (index1 != index2) {
index1 = index1.next;
index2 = index2.next;
}
return index1;
}
}
// 链表中没有环返回null
return null;
}
}
147. 对链表进行插入排序
给定单个链表的头 head ,使用插入排序对链表进行排序,并返回排序后链表的头 。
插入排序算法的步骤:
- 插入排序是迭代的,每次只移动一个元素,直到所有元素可以形成一个有序的输出列表。
- 每次迭代中,插入排序只从输入数据中移除一个待排序的元素,找到它在序列中适当的位置,并将其插入。
- 重复直到所有输入数据插入完为止。
思路就是从前往后遍历,不满足顺序的节点(小的在前,大的在后),再从前往后找到该节点要插入的位置(因为是单链表只能这样找)。
class Solution {
public ListNode insertionSortList(ListNode head) {
ListNode dummy = new ListNode(-1);
ListNode pre;
dummy.next = head;
while (head.next != null) {
if (head.val <= head.next.val) {
head = head.next;
continue;
}
pre = dummy;
// 从前往后找到要插入的位置,循环退出的条件是当pre的下一个节点元素大于head.next.val
// 说明pre后面应该连接上head.next
// 这里体现了添加dummyHead的好处
while (pre.next.val < head.next.val) {
pre = pre.next;
}
ListNode cur = head.next;
head.next = cur.next;
cur.next = pre.next;
pre.next = cur;
}
return dummy.next;
}
}
148. 排序链表⭐⭐
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
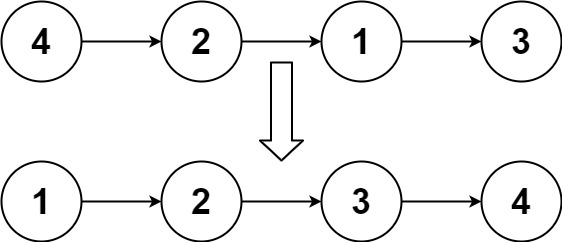
第一种解法:使用优先级队列
class Solution {
public ListNode sortList(ListNode head) {
if (head == null) {
return null;
}
PriorityQueue<ListNode> queue = new PriorityQueue<>((n1, n2) -> n1.val - n2.val);
// 将链表中的每一个节点都放入堆中
while (head != null) {
queue.offer(head);
head = head.next;
}
ListNode dummyHead = new ListNode(-1);
ListNode cur = dummyHead;
while (!queue.isEmpty()) {
// 这里一定要重新创建节点,否则会造成环。
cur.next = new ListNode(queue.poll().val);
cur = cur.next;
}
return dummyHead.next;
}
}
第二种解法:使用归并排序
class Solution {
public ListNode sortList(ListNode head) {
// 题目说明了链表中节点的数目有可能是0,所以需要做特殊处理。
if (head == null) {
return null;
}
ListNode mid = getMid(head);
// 找到mid节点的下一个节点是null,说明链表中只有一个节点,返回这个节点。
if (mid.next == null) {
return mid;
}
ListNode headB = mid.next;
// 断链操作
mid.next = null;
return mergeTwoList(sortList(head), sortList(headB));
}
// 找到链表的中间节点,这里加dummy节点的原因是保证在链表有偶数个节点时,找到正确的中间节点。并且能够在链表只有一个节点时,不会出现空指针异常。
public ListNode getMid(ListNode head) {
head = new ListNode(0, head);
ListNode slow = head;
ListNode fast = head;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
}
// 当fast == null时,slow指针指向的值就是中间节点的位置。
return slow;
}
// 合并两个有序链表
public ListNode mergeTwoList(ListNode l1, ListNode l2) {
ListNode dummy = new ListNode();
ListNode last = dummy;
while (l1 != null && l2 != null) {
if (l1.val <= l2.val) {
last.next = l1;
l1 = l1.next;
} else {
last.next = l2;
l2 = l2.next;
}
// 将last移动到已完成合并链表的最后
last = last.next;
}
if (l1 != null) {
last.next = l1;
}
if (l2 != null) {
last.next = l2;
}
return dummy.next;
}
}
第三种解法:使用快速排序 (字节面试考察过,但是这样会超时)
class Solution {
public ListNode sortList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
quickSort(head, null);
return head;
}
// [left, right)
public void quickSort(ListNode head, ListNode right) {
if (head == right) {
return;
}
ListNode left = head;
// 循环不变量
// all ListNode in [left.next, j] val <= target
// all ListNode in (j, cur) val > target
// 把j看作是第一个区间的最后一个节点
int target = left.val;
ListNode j = left;
ListNode cur = left.next;
while (cur != right) {
if (cur.val <= target) {
j = j.next;
int temp = cur.val;
cur.val = j.val;
j.val = temp;
}
cur = cur.next;
}
int tmp = j.val;
j.val = left.val;
left.val = tmp;
// 这里是左闭右开,因为while循环的判断是cur!=right,当cur==right时就不满足条件。
// 因为单向链表
quickSort(head, j);
quickSort(j.next, right);
}
}
160. 相交链表
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交:

常规解法:
class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode curA = headA;
ListNode curB = headB;
int lenA = 0, lenB = 0;
while (curA != null) { // 求链表A的长度
lenA++;
curA = curA.next;
}
while (curB != null) { // 求链表B的长度
lenB++;
curB = curB.next;
}
curA = headA;
curB = headB;
// 让curA指向最长链表的头,lenA为其长度
if (lenB > lenA) {
//1. swap (lenA, lenB);
int tmpLen = lenA;
lenA = lenB;
lenB = tmpLen;
//2. swap (curA, curB);
ListNode tmpNode = curA;
curA = curB;
curB = tmpNode;
}
// 求长度差
int gap = lenA - lenB;
// 让curA和curB在同一起点上(末尾位置对齐)
while (gap-- > 0) {
curA = curA.next;
}
// 遍历curA 和 curB,遇到相同则直接返回
while (curA != null) {
if (curA == curB) {
return curA;
}
curA = curA.next;
curB = curB.next;
}
return null;
}
}
双指针解法:
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode A = headA, B = headB;
while (A != B) {
A = A != null ? A.next : headB;
B = B != null ? B.next : headA;
}
return A;
}
}
234. 回文链表⭐
给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。

输入:head = [1,2,2,1]
输出:true
我自己写的笨方法
首先用快慢指针,找到链表的中间节点,然后判断链表总数有多少个,再根据链表总数是奇数还是偶数来确定后面部分的起始节点。
class Solution {
public boolean isPalindrome(ListNode head) {
ListNode dummy = new ListNode(-1, head);
ListNode fast = dummy;
ListNode slow = dummy;
ListNode pre = dummy;
ListNode second;
int size;
int count = 0;
// 通过快慢指针找到链表的中间节点
while (fast != null && fast.next != null) {
fast = fast.next.next;
pre = slow;
slow = slow.next;
count++;
}
// 当fast != null时说明链表有偶数个节点
if (fast != null) {
size = 2 * count;
} else {
size = 2 * count - 1;
}
// 两个特殊情况
if (size == 1) {
return true;
}
if (size == 2) {
if (head.val != head.next.val) {
return false;
} else {
return true;
}
}
// 如果是偶数节点那么中间节点不止一个
if (size % 2 == 0) {
// 中间的两个元素不等,说明不是回文链表了。
if (slow.val != slow.next.val) {
return false;
}
second = slow.next.next;
} else {
second = slow.next;
}
pre.next = null;
// 反转第二部分链表
ListNode node = reverse(second);
// 比较两部分链表对应节点的值是否相等。
while (head != null && node != null) {
if (head.val != node.val) {
return false;
}
head = head.next;
node = node.next;
}
return true;
}
private ListNode reverse(ListNode head) {
ListNode prev = null;
ListNode cur = head;
while (cur != null) {
ListNode nextNode = cur.next;
cur.next = prev;
prev = cur;
cur = nextNode;
}
// 当 cur == null 时,此时prev就是新的链表头
return prev;
}
}
在利用快慢指针找链表中间节点的过程中,就将链表前半部分反转了。
class Solution {
public boolean isPalindrome(ListNode head) {
if (head == null || head.next == null) {
return true;
}
ListNode slow = head, fast = head;
ListNode pre = head, prepre = null;
while (fast != null && fast.next != null) {
pre = slow;
slow = slow.next;
fast = fast.next.next;
pre.next = prepre;
prepre = pre;
}
if (fast != null) {
slow = slow.next;
}
while (pre != null && slow != null) {
if (pre.val != slow.val) {
return false;
}
pre = pre.next;
slow = slow.next;
}
return true;
}
}
链表的后序遍历,借助函数调用栈。
class Solution {
// 左侧指针
ListNode left;
boolean isPalindrome(ListNode head) {
left = head;
return traverse(head);
}
boolean traverse(ListNode right) {
if (right == null) {
return true;
}
boolean res = traverse(right.next);
// 后序遍历代码
res = res && (right.val == left.val);
left = left.next;
return res;
}
}
328. 奇偶链表
给定单链表的头节点 head ,将所有索引为奇数的节点和索引为偶数的节点分别组合在一起,然后返回重新排序的列表。
第一个节点的索引被认为是奇数 , 第二个节点的索引为偶数 ,以此类推。
请注意,偶数组和奇数组内部的相对顺序应该与输入时保持一致。
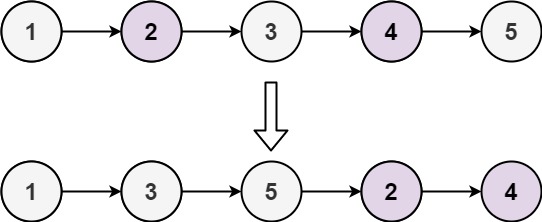
class Solution {
public ListNode oddEvenList(ListNode head) {
if (head == null) {
return null;
}
ListNode cur = head; // 奇数位置节点
ListNode temp = cur.next; // 偶数位置节点
ListNode dummy = temp; // 偶数位置头节点,方便后续拼接
while (temp != null && temp.next != null) {
cur.next = cur.next.next; // 奇数位置指向下一个奇数位置
temp.next = temp.next.next; // 偶数位置指向下一个偶数位置
cur = cur.next;
temp = temp.next;
}
cur.next = dummy; // 奇数位置尾节点拼接上偶数节点头节点
return head;
}
}
86. 分隔链表
给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。
你应当 保留 两个分区中每个节点的初始相对位置。
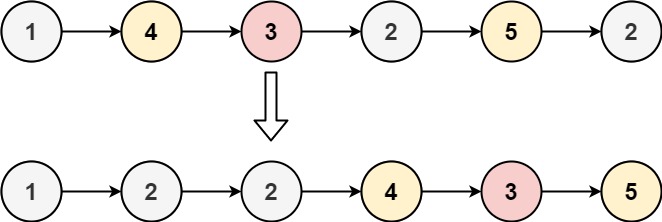
class Solution {
public ListNode partition(ListNode head, int x) {
if (head == null) {
return head;
}
ListNode dummyA = new ListNode(-1);
ListNode dummyB = new ListNode(-1);
ListNode headA = dummyA;
ListNode headB = dummyB;
// 在遍历链表的同时,分别把节点值小于x的节点连起来,把节点值大于等于x的节点连起来
while (head != null) {
if (head.val < x) {
headA.next = head;
head = head.next;
headA = headA.next;
headA.next = null;
} else {
headB.next = head;
head = head.next;
headB = headB.next;
headB.next = null;
}
}
// 将两部分链表接上,因为一开始就用dummyA和dummyB分别指向了两部分链表的头部。
headA.next = dummyB.next;
return dummyA.next;
}
}
725. 分隔链表⭐
给你一个头结点为 head 的单链表和一个整数 k ,请你设计一个算法将链表分隔为 k 个连续的部分。
每部分的长度应该尽可能的相等:任意两部分的长度差距不能超过 1 。这可能会导致有些部分为 null 。
这 k 个部分应该按照在链表中出现的顺序排列,并且排在前面的部分的长度应该大于或等于排在后面的长度。
返回一个由上述 k 部分组成的数组。

输入:head = [1,2,3,4,5,6,7,8,9,10], k = 3
输出:[[1,2,3,4],[5,6,7],[8,9,10]]
解释:输入被分成了几个连续的部分,并且每部分的长度相差不超过 1 。前面部分的长度大于等于后面部分的长度。
class Solution {
public ListNode[] splitListToParts(ListNode head, int k) {
int cnt = 0;
// 求出链表的长度
ListNode cur = head;
while (cur != null) {
cur = cur.next;
cnt++;
}
// carry代表的是将cnt个链表节点平均分成k组,还剩下的个数。
int carry = cnt % k;
// 每一组平均节点个数
int average = cnt / k;
cur = head;
ListNode pre = new ListNode(-1);
ArrayList<ListNode> ans = new ArrayList<>();
while (cur != null) {
ans.add(cur);
// 这样往后找会让cur指向下一组的开始节点
for (int i = 0; i < average; i++) {
pre = cur;
cur = cur.next;
}
// 如果carry > 0,说明此时正在处理的这一组,节点数应该为 average + 1。
if (carry > 0) {
carry--;
pre = cur;
cur = cur.next;
}
// 断开这一组节点
pre.next = null;
}
// 如果链表总节点数小于k,剩下的位置用null占满。
int empty = k - ans.size();
for (int i = 0; i < empty; i++) {
ans.add(null);
}
// 将ArrayList转换为数组
return ans.toArray(new ListNode[k]);
}
}
876. 链表的中间结点⭐
给定一个头结点为 head 的非空单链表,返回链表的中间结点。
如果有两个中间结点,则返回第二个中间结点。
/**
* 本题的思路是采用快慢指针,当快指针不能移动时,慢指针指向的即为题目所要求的中间节点。
* 题目要求的是如果有两个中间节点,则返回第二个中间节点。
* 因此,对于该题目而言,快指针fast向前移动的条件是:fast != null && fast.next != null。
*/
class Solution {
public ListNode middleNode(ListNode head) {
ListNode slow = head;
ListNode fast = head;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
}
return slow;
}
}
2095. 删除链表的中间节点
class Solution {
public ListNode deleteMiddle(ListNode head) {
if (head.next == null) {
return null;
}
ListNode pre = head;
ListNode fast = head;
ListNode slow = head;
while (fast != null && fast.next != null) {
pre = slow;
fast = fast.next.next;
slow = slow.next;
}
pre.next = slow.next;
return head;
}
}
字符串
5. 最长回文子串😭
给你一个字符串 s,找到 s 中最长的回文子串。
第一种解法:中心扩散法
中心扩散法也很好理解,我们遍历字符串的每一个字符,然后以当前字符为中心往两边扩散,查找最长的回文子串。



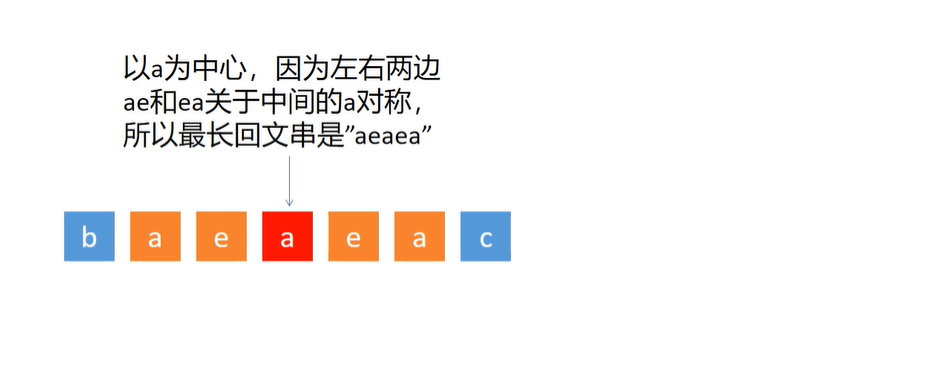
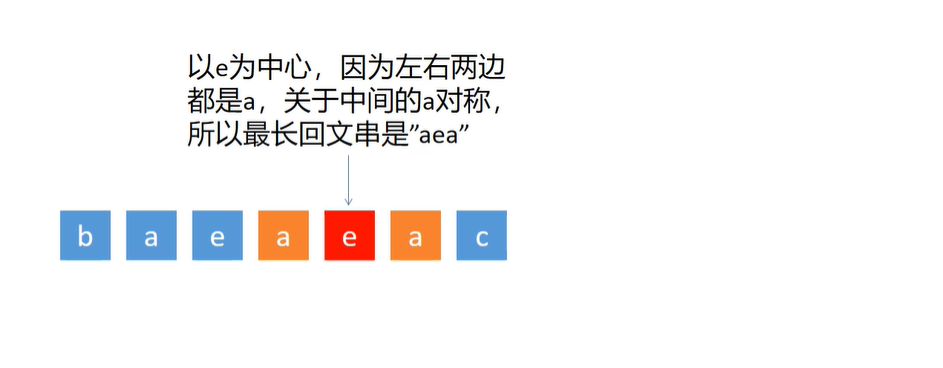
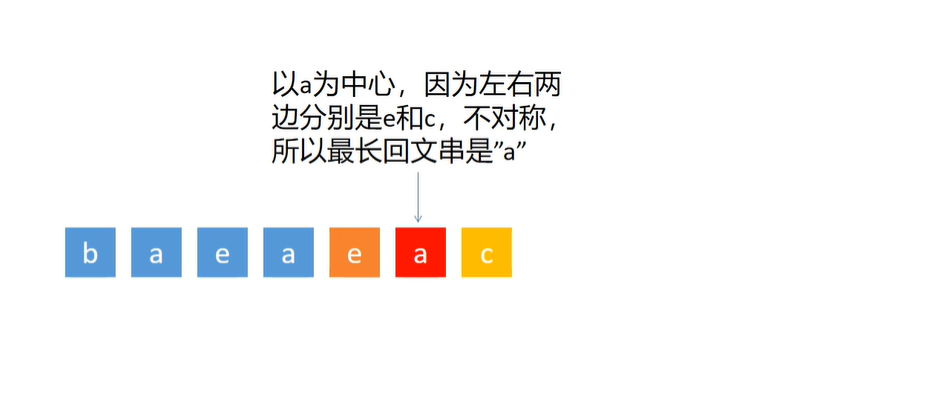
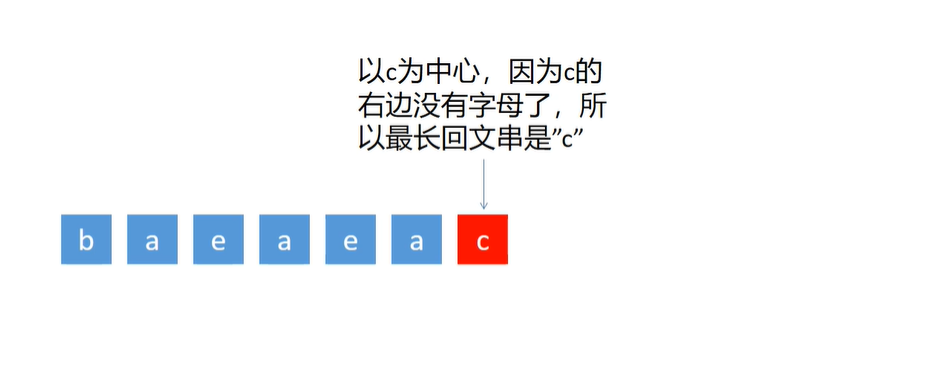
以每一个字符为中心,往两边扩散,来求最长的回文子串。
但忽略了一个问题,回文串的长度不一定都是奇数,也可能是偶数,比如字符串"abba",如果使用上面的方式判断肯定是不对的。
我们来思考这样一个问题,如果是单个字符,我们可以认为他是回文子串,如果是多个字符,并且他们都是相同的,那么他们也是回文串。
所以对于上面的问题,我们以当前字符为中心往两边扩散的时候,先要判断和他挨着的有没有相同的字符,如果有,则直接跳过,来看下代码。
class Solution {
public String longestPalindrome(String s) {
// 当字符串长度小于2时,直接返回字符串。
if (s.length() < 2) {
return s;
}
int start = 0;
int maxLen = 0;
int length = s.length();
for (int i = 0; i < length()) {
// 当剩余字符串长度小于当前maxLen的一半,那剩下的数构成回文也没有maxLen。
if (length - i < maxLen / 2) {
break;
}
int left = i;
int right = i;
// 遇到下一个相同的字符就跳过
while (right < length - 1 && s.charAt(right) == s.charAt(right + 1)) {
right++;
}
// 下一次循环从这里开始,有可能跳过了相同的字符所在的下标。
i = right + 1;
// 注意两个边界取值。
// 往左右两边扩散,当左右字符相同时,继续扩散。
while (right < length - 1 && left > 0 && s.charAt(left - 1) == s.charAt(right + 1)) {
left--;
right++;
}
// 比较回文串最长长度
if (right - left + 1 > maxLen) {
// 记录当前回文串的开始位置
start = left;
maxLen = right - left + 1;
}
}
// 截取字符串,注意substring,string没有大写,且截取的字符串是左闭右开的。
return s.substring(start, start + maxLen);
}
}
第二种解法:马拉车算法
我们先看一下回文串,回文串有两种形式,一种是奇数的比如"aba",一种是偶数的比如"abba"。这里使用Manacher算法的时候,会在每个字符之间都会插入一
个特殊字符,并且两边也会插入,这个特殊字符要保证不能是原字符串中的字符,这样无论原来字符串长度是奇数还是偶数,添加之后长度都会变成奇数。例如
"aba"-->"#a#b#a#"(长度是7)
"abba"-->"#a#b#b#a#"(长度是9)
这里再来引用一个变量叫回文半径,通过添加特殊字符,原来字符串长度无论是奇数还是偶数最终都会变为奇数,因为特殊字符的引用,改变之后的字符串的所有
回文子串长度一定都是奇数。并且回文子串的第一个和最后一个字符一定是你添加的那个特殊字符。
因为添加特殊字符之后所有回文子串的长度都是奇数,我们定义回文子串最中间的那个字符到回文子串最左边的长度叫回文半径,如下图所示。
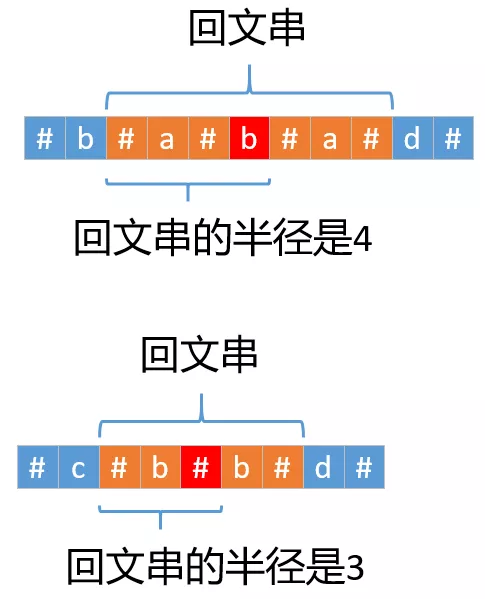
class Solution {
public String longestPalindrome(String s) {
int charLen = s.length();
int length = 2 * charLen + 1;
int[] chars = s.toCharArray();
int[] res = new int[length];
int index = 0;
for (int i = 0; i < length; i++) {
res[i] = (i % 2) == 0 ? '#' : chars[index++];
}
int maxCenter, maxRight, resCenter, resLen;
for (int i = 0; i < length; i++) {
if (i < maxRight) {
if (p[2 * maxCenter - i] < p[maxRight - i]) {
p[i] = p[2 * maxCenter - i];
} else {
p[i] = maxRight - i;
while (i - p[i] >= 0 && i + p[i] <= length - 1 && res[i - p[i]] == res[i + p[i]]) {
p[i]++;
}
}
} else {
p[i] = 1;
while (i - p[i] >= 0 && i + p[i] <= length - 1 && res[i - p[i]] == res[i + p[i]]) {
p[i]++;
}
}
if (i + p[i] > maxRight) {
maxRight = i + p[i];
maxCenter = i;
}
if (p[i] > resLen) {
resLen = p[i];
resCenter = i;
}
}
resLen = resLen - 1;
int start = (resCenter - resLen) >> 1;
return s.substring(start, start + resLen);
}
}
647. 字符串中回文子串的个数⭐🐱🏍
给你一个字符串 s ,请你统计并返回这个字符串中回文子串的数目。
回文字符串是正着读和倒过来读一样的字符串。
子字符串是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
解法一:暴力
class Solution {
public int countSubstrings(String s) {
if (s.length() < 2) {
return 1;
}
char[] chars = s.toCharArray();
int count = 0;
for (int i = 0; i < s.length() - 1; i++) {
for (int j = i + 1; j < s.length(); j++) {
if (validPalindromic(chars, i, j)) {
count++;
}
}
}
return count + s.length();
}
public boolean validPalindromic(char[] chars, int i, int j) {
while (i < j) {
if (chars[i] != chars[j]) {
return false;
}
i++;
j--;
}
return true;
}
}
解法2:中心扩散法
class Solution {
private int ans = 0;
public int countSubstrings(String s) {
for (int i = 0; i < s.length(); i++) {
// 以单个字母为中心的情况
isPalindromic(s, i, i);
// 以两个字母为中心的情况
isPalindromic(s, i, i + 1);
}
return ans;
}
// 中心扩散
private void isPalindromic(String s, int i, int j) {
while (i >= 0 && j < s.length()) {
if (s.charAt(i) != s.charAt(j)) {
return;
}
i--;
j++;
ans++; // 移动的过程中只要移动两个指针之后,指向字符还相等ans就加1。
}
}
}
解法3:动态规划 (区间DP)
这题让求一个字符串中有多少个回文子串,子串必须是连续的,子序列可以不连续,这题可以使用动态规划来解决。
定义dp[i] [j]:表示字符串s从下标i到j是否是回文串,如果dp[i] [j]是true,则表示是回文串,否则不是回文串。
如果要计算dp[i] [j],首先要判断s.charAt(i) == s.charAt(j)是否成立。
1、如果s.charAt(i) != s.charAt(j),那么dp[i] [j]肯定不能构成回文串。如下图所示:

2、如果s.charAt(i) == s.charAt(j),我们还需要判断dp[i+1] [j-1]是否是回文串,如下图所示:
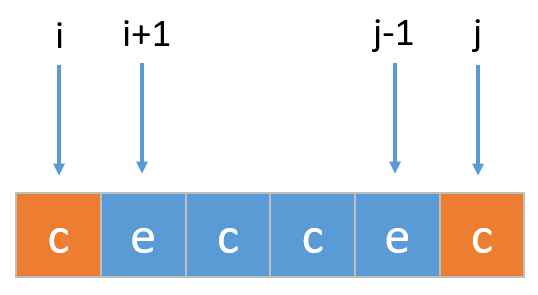
实际上如果i和j离的非常近的时候,比如 j - i <= 2,我们也可以认为dp[i] [j]是回文子串,如下图所示:

但是这里有个问题,如果我们想要求dp[i] [j]还需要知道dp[i+1] [j-1],如下图所示:

我们可以从左往右,从上往下开始计算,这样也能保证在计算dp[i] [j]的时候,dp[i+1] [j-1]已经计算过了,如下图所示:

最终代码如下:
class Solution {
public int countSubstrings(String s) {
int n = s.length(), ans = 0;
// dp[i][j]:s字符串下标i到下标j的字串是否是一个回文串,即s[i, j]。
boolean[][] dp = new boolean[n][n];
// 这里注意遍历的顺序。
for (int j = 0; j < n; j++) {
for (int i = 0; i <= j; i++) {
// 当两端字母一样时,才可以两端收缩进一步判断。
if (s.charAt(i) == s.charAt(j)) {
// i++,j--,即两端收缩之后i,j指针指向同一个字符或者i超过j了,必然是一个回文串。
if (j - i <= 2) {
dp[i][j] = true;
} else {
// 否则通过收缩之后的子串判断。根据左下方进行更新。
dp[i][j] = dp[i + 1][j - 1];
}
}
}
}
// 因为dp数组记录了某一个区间是不是回文串。
// 遍历每一个子串,统计回文串个数。
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (dp[i][j]) {
ans++;
}
}
}
return ans;
}
}
409. 最长回文串😭
给定一个包含大写字母和小写字母的字符串 s ,返回通过这些字母构造成的最长的回文串。
在构造过程中,请注意区分大小写 。比如 "Aa" 不能当做一个回文字符串。
解题思路:回文串如果是由奇数个字符构成的,那么只能有一个字符没有配对。
比如abcccba,就只有中间的c没有和任何字符配对,它处于回文串的中间。
class Solution {
public int longestPalindrome(String s) {
// 找出可以构成最长回文串的长度
int[] arr = new int[128];
for(char c : s.toCharArray()) {
arr[c]++;
}
int count = 0;
for (int i : arr) {
// 统计有多少个出现了奇数次的字符
count += (i % 2);
}
return count == 0 ? s.length() : (s.length() - count + 1);
}
}
8. 字符串转换整数 (atoi)
这道题就是按照题目的要求来:
1、去除前导空格;
2、判断符号(默认是正);
3、将字符转换为数字并注意越界的处理;
4、返回数字乘以符号。
class Solution {
public int myAtoi(String s) {
int length = s.length();
int index = 0;
// 一定要加上这个index < length的判断,否则遇到全是空格的字符串" "会报空指针异常
// 1、去除前导空格
while (index < length && s.charAt(index) == ' ') {
index++;
}
// 到这一步index == length了说明字符串全是空格
if (index == length) {
return 0;
}
// 符号肯定是在数字的前面咯,这里先进判断是什么符号。
// 不存在符号时默认为正
// 2、判断符号
int sign = 1;
if (s.charAt(index) == '+') {
index++;
} else if (s.charAt(index) == '-') {
sign = -1;
index++;
}
final int MAX = Integer.MAX_VALUE / 10;
int num = 0;
// 将字符转换为数字,转换过程中注意越界的处理。
// Character.isDigit判断一个char字符是不是数字
while (index < length && Character.isDigit(s.charAt(index))) {
int digit = s.charAt(index) - '0';
if (num > MAX) {
return sign > 0 ? Integer.MAX_VALUE : Integer.MIN_VALUE;
} else if (num == MAX) {
if (sign > 0 && digit > 7) {
return Integer.MAX_VALUE;
} else if (sign < 0 && digit > 8) {
return Integer.MIN_VALUE;
}
}
num = num * 10 + digit;
index++;
}
return num * sign;
}
}
125. 验证回文串⭐
给定一个字符串,验证它是否是回文串,只考虑字母和数字字符,可以忽略字母的大小写。
说明:本题中,我们将空字符串定义为有效的回文串。
输入: "A man, a plan, a canal: Panama"
输出: true
解释:"amanaplanacanalpanama" 是回文串
/**
* 这道题我看主要是考察API的使用
* 1、Character.isLetterOrDigit(char ch)判断ch是否是字母或者数字;
* 2、Character.toLowerCase(char ch)将字母大写转小写。
*/
class Solution {
public boolean isPalindrome(String s) {
int n = s.length();
// 左右指针
int left = 0, right = n - 1;
while (left < right) {
// 遇到字符或者是数字,让左指针停在那,接着让右指针移动。
while (left < right && !Character.isLetterOrDigit(s.charAt(left))) {
left++;
}
while (left < right && !Character.isLetterOrDigit(s.charAt(right))) {
right--;
}
if (left < right) {
if (Character.toLowerCase(s.charAt(left)) != Character.toLowerCase(s.charAt(right))) {
return false;
}
left++;
right--;
}
}
return true;
}
}
68. 文本左右对齐
151. 颠倒字符串中的单词
给你一个字符串 s ,颠倒字符串中 单词 的顺序。
单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。
返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。
注意:输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中,单词间应当仅用单个空格分隔,且不包含任何额外的空格。
输入:s = "the sky is blue"
输出:"blue is sky the"
思路就是先去除字符串前后的空格,然后用 i 和 j 从字符串末尾开始搜索单词。
class Solution {
public String reverseWords(String s) {
// 1、去掉前后的空格
int start = 0;
int end = s.length() - 1;
while (start <= end && s.charAt(start) == ' ') {
start++;
}
while (start <= end && s.charAt(end) == ' ') {
end--;
}
s = s.substring(start, end + 1);
int j = s.length() - 1, i = j;
StringBuilder res = new StringBuilder();
while (i >= 0) {
while (i >= 0 && s.charAt(i) != ' ') {
i--; // 搜索首个空格
}
// 截取i+1到j的字符
res.append(s.substring(i + 1, j + 1) + " "); // 添加单词
while (i >= 0 && s.charAt(i) == ' ') {
i--; // 跳过单词间空格
}
j = i; // j 指向下个单词的尾字符
}
// 去掉最后的空格我还是用了trim()要是面试官不让用trim那就像上面一样处理就行了。
return res.toString().trim(); // 转化为字符串并返回
}
}
316. 去除重复字母⭐⭐⭐⭐
给你一个字符串 s ,请你去除字符串中重复的字母,使得每个字母只出现一次。
需保证 返回结果的字典序最小(要求不能打乱其他字符的相对位置)。
题目的要求总结出来有三点:
要求一、要去重;
要求二、去重字符串中的字符顺序不能打乱 s 中字符出现的相对顺序;
要求三、在所有符合上一条要求的去重字符串中,字典序最小的作为最终结果。
上述三条要求中,要求三可能有点难理解,举个例子。
比如说输入字符串 s = "babc",去重且符合相对位置的字符串有两个,分别是 "bac" 和 "abc",但是我们的算法得返回 "abc",因为它的字典序更小。
按理说,如果我们想要有序的结果,那就得对原字符串排序对吧,但是排序后就不能保证符合 s 中字符出现顺序了,这似乎是矛盾的。
其实这里会借鉴前文 单调栈解题框架 中讲到的「单调栈」的思路,没看过也无妨,等会你就明白了。
我们先暂时忽略要求三,用「栈」来实现一下要求一和要求二,至于为什么用栈来实现,后面你就知道了:
String removeDuplicateLetters(String s) {
// 存放去重的结果
Stack<Character> stk = new Stack<>();
// 布尔数组初始值为 false,记录栈中是否存在某个字符
// 输入字符均为 ASCII 字符,所以大小 256 够用了
boolean[] inStack = new boolean[256];
for (char c : s.toCharArray()) {
// 如果字符 c 存在栈中,直接跳过
if (inStack[c]) {
continue;
}
// 若不存在,则插入栈顶并标记为存在
stk.push(c);
inStack[c] = true;
}
StringBuilder sb = new StringBuilder();
while (!stk.empty()) {
sb.append(stk.pop());
}
// 栈中元素插入顺序是反的,需要 reverse 一下
return sb.reverse().toString();
}
这段代码的逻辑很简单吧,就是用布尔数组 inStack 记录栈中元素,达到去重的目的,此时栈中的元素都是没有重复的。
如果输入 s = "bcabc",这个算法会返回 "bca",已经符合要求一和要求二了,但是题目希望要的答案是 "abc" 对吧。
那我们想一想,如果想满足要求三,保证字典序,需要做些什么修改?
在向栈 stk 中插入字符 'a' 的这一刻,我们的算法需要知道,字符 'a' 的字典序和之前的两个字符 'b' 和 'c' 相比,谁大谁小?
如果当前字符 'a' 比之前的字符字典序小,就有可能需要把前面的字符 pop 出栈,让 'a' 排在前面,对吧?
那么,我们先改一版代码:
String removeDuplicateLetters(String s) {
Stack<Character> stk = new Stack<>();
boolean[] inStack = new boolean[256];
for (char c : s.toCharArray()) {
if (inStack[c]) continue;
// 插入之前,和之前的元素比较一下大小
// 如果字典序比前面的小,pop 前面的元素
while (!stk.isEmpty() && stk.peek() > c) {
// 弹出栈顶元素,并把该元素标记为不在栈中
inStack[stk.pop()] = false;
}
stk.push(c);
inStack[c] = true;
}
StringBuilder sb = new StringBuilder();
while (!stk.empty()) {
sb.append(stk.pop());
}
return sb.reverse().toString();
}
这段代码也好理解,就是插入了一个 while 循环,连续 pop 出比当前字符小的栈顶字符,直到栈顶元素比当前元素的字典序还小为止。只是不是有点「单调栈」的意思了?
这样,对于输入 s = "bcabc",我们可以得出正确结果 "abc" 了。
但是,如果我改一下输入,假设 s = "bcac",按照刚才的算法逻辑,返回的结果是 "ac",而正确答案应该是 "bac",分析一下这是怎么回事?
很容易发现,因为 s 中只有唯一一个 'b',即便字符 'a' 的字典序比字符 'b' 要小,字符 'b' 也不应该被 pop 出去。
那问题出在哪里?
我们的算法在 stk.peek() > c 时才会 pop 元素,其实这时候应该分两种情况:
情况一、如果 stk.peek() 这个字符之后还会出现,那么可以把它 pop 出去,反正后面还有嘛,后面再 push 到栈里,刚好符合字典序的要求。
情况二、如果 stk.peek() 这个字符之后不会出现了,前面也说了栈中不会存在重复的元素,那么就不能把它 pop 出去,否则你就永远失去了这个字符。
回到 s = "bcac" 的例子,插入字符 'a' 的时候,发现前面的字符 'c' 的字典序比 'a' 大,且在 'a' 之后还存在字符 'c',那么栈顶的这个 'c' 就会被 pop 掉。
while 循环继续判断,发现前面的字符 'b' 的字典序还是比 'a' 大,但是在 'a' 之后再没有字符 'b' 了,所以不应该把 'b' pop 出去。
那么关键就在于,如何让算法知道字符 'a' 之后有几个 'b' 有几个 'c' 呢?
也不难,只要再改一版代码:
String removeDuplicateLetters(String s) {
Stack<Character> stk = new Stack<>();
// 维护一个计数器记录字符串中字符的数量
// 因为输入为 ASCII 字符,大小 256 够用了
int[] count = new int[256];
for (int i = 0; i < s.length(); i++) {
count[s.charAt(i)]++;
}
boolean[] inStack = new boolean[256];
for (char c : s.toCharArray()) {
// 每遍历过一个字符,都将对应的计数减一
count[c]--;
if (inStack[c]) continue;
while (!stk.isEmpty() && stk.peek() > c) {
// 若之后不存在栈顶元素了,则停止 pop
if (count[stk.peek()] == 0) {
break;
}
// 若之后还有,则可以 pop
inStack[stk.pop()] = false;
}
stk.push(c);
inStack[c] = true;
}
StringBuilder sb = new StringBuilder();
while (!stk.empty()) {
sb.append(stk.pop());
}
return sb.reverse().toString();
}
我们用了一个计数器 count,当字典序较小的字符试图「挤掉」栈顶元素的时候,在 count 中检查栈顶元素是否是唯一的,只有当后面还存在栈顶元素的时候才能挤掉,否则不能挤掉。
至此,这个算法就结束了,时间空间复杂度都是 O(N)。
你还记得我们开头提到的三个要求吗?我们是怎么达成这三个要求的?
要求一、通过 inStack 这个布尔数组做到栈 stk 中不存在重复元素。
要求二、我们顺序遍历字符串 s,通过「栈」这种顺序结构的 push/pop 操作记录结果字符串,保证了字符出现的顺序和 s 中出现的顺序一致。
这里也可以想到为什么要用「栈」这种数据结构,因为先进后出的结构允许我们立即操作刚插入的字符,如果用「队列」的话肯定是做不到的。
要求三、我们用类似单调栈的思路,配合计数器 count 不断 pop 掉不符合最小字典序的字符,保证了最终得到的结果字典序最小。
当然,由于栈的结构特点,我们最后需要把栈中元素取出后再反转一次才是最终结果。
394. 字符串解码
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
输入:s = "3[a]2[bc]"
输出:"aaabcbc"
class Solution {
public String decodeString(String s) {
Stack<Character> stack = new Stack<>();
for (Character ch : s.toCharArray()) {
if (ch != ']') {
stack.push(ch);
}
if (ch == ']') {
StringBuilder sb = new StringBuilder();
while (true) {
Character c = stack.pop();
if (c == '[') {
break;
} else {
sb.append(c);
}
}
sb.reverse();
StringBuilder numc = new StringBuilder();
while (!stack.isEmpty() && Character.isDigit(stack.peek())) {
Character num = stack.pop();
if (Character.isDigit(num)) {
numc.append(num);
} else {
break;
}
}
int count = Integer.parseInt(numc.reverse().toString());
String zhuijia = sb.toString();
for (int i = 0; i < count - 1; i++) {
sb.append(zhuijia);
}
for (Character c : sb.toString().toCharArray()) {
stack.push(c);
}
}
}
StringBuilder res = new StringBuilder();
while (!stack.isEmpty()) {
res.append(stack.pop());
}
return res.reverse().toString();
}
}
438. 找到字符串中所有字母异位词
给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
滑动窗口解法:
class Solution {
public List<Integer> findAnagrams(String s, String p) {
HashMap<Character, Integer> need = new HashMap<>();
HashMap<Character, Integer> window = new HashMap<>();
List<Integer> res = new ArrayList<>();
for (Character ch : p.toCharArray()) {
need.put(ch, need.getOrDefault(ch, 0) + 1);
}
int left = 0, right = 0;
int start = 0, len = Integer.MAX_VALUE;
int valid = 0;
while (right < s.length()) {
char c = s.charAt(right);
right++;
if (need.containsKey(c)) {
window.put(c, window.getOrDefault(c, 0) + 1);
if (window.get(c).equals(need.get(c))) {
valid++;
}
}
if (right - left == p.length()) {
start = left;
if (valid == need.size()) {
res.add(start);
}
char d = s.charAt(left);
left++;
if (need.containsKey(d)) {
if (window.get(d).equals(need.get(d))) {
valid--;
}
window.put(d, window.get(d) - 1);
}
}
}
return res;
}
}
680. 验证回文字符串 Ⅱ⭐⭐
给定一个非空字符串 s,最多删除一个字符。判断是否能成为回文字符串。
输入: s = "abca"
输出: true
解释: 你可以删除c字符。
判断回文串显然是用双指针的,i从前往后遍历,j从后往前遍历。难点就是怎么去判断删除一个元素后的字符串是不是回文串,我提供一个思路:
以"abdda"这个串为例,此时i指向'b',j指向'd',发现不对了。但是有一次删除的机会,我们自己写几个case其实就能发现,此时子串范围为(i+1, j)或(i, j-1)的俩子
串只要有任意一个是回文串,则结果就是回文串,否则就不是。
class Solution {
public boolean validPalindrome(String s) {
int left = 0, right = s.length() - 1;
while (left < right) {
if (s.charAt(left) != s.charAt(right)) {
return isValid(s, left + 1, right) || isValid(s, left, right - 1);
}
left++;
right--;
}
return true;
}
private boolean isValid(String s, int start, int end) {
while (start < end) {
if (s.charAt(start) != s.charAt(end)) {
return false;
}
start++;
end--;
}
return true;
}
}
双指针
42. 接雨水⭐⭐⭐
参考题解:https://labuladong.gitee.io/algo/4/33/129/
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

解法一:暴力
class Solution {
public int trap(int[] height) {
int ans = 0;
int n = height.length;
// 索引下标为0的柱子也就是最左边的柱子肯定是不能存雨水的
// 索引下标为n - 1的柱子也就是最右边的柱子也是不能存水的
// 除去最左和最右两边的柱子,遍历剩下的柱子,遍历时求出每根柱子左边最高柱子的高度以及右边最高柱子的高度。
for (int i = 1; i < n - 1; i++) {
int cur = height[i];
for (int k = i - 1; k >= 0; k--) {
l = Math.Max(l, height[k]);
}
// 若左边最高的柱子小于等于当前柱子那这根柱子肯定存不下水。
if (cur >= l) {
continue;
}
int r = Integer.MAX_VALUE;
for (int k = j + 1; j < n; j++) {
r = Math.max(r, height[j]);
}
// 若右边最高的柱子小于等于当前柱子那这根柱子也存不下水。
if (cur >= r) {
continue;
}
ans = ans + Math.min(l, r) - cur;
}
return ans;
}
}
解法二:备忘录
class Solution {
public int trap(int[] height) {
if (height.length == 0) {
return 0;
}
int n = height.length;
int res = 0;
// 数组充当备忘录,计算出每个索引位置i左右两边最高的柱子的高度。
int[] l_max = new int[n];
int[] r_max = new int[n];
// 初始化 base case
// 0索引位置左边最高的柱子是它自己。
l_max[0] = height[0];
// n - 1索引位置右边最高的柱子是它自己。
r_max[n - 1] = height[n - 1];
// 从左向右计算 l_max
for (int i = 1; i < n; i++) {
l_max[i] = Math.max(height[i], l_max[i - 1]);
}
// 从右向左计算 r_max
for (int i = n - 2; i >= 0; i--) {
r_max[i] = Math.max(height[i], r_max[i + 1]);
}
// 计算答案
// 每个柱子能存水的数量是左右两边最高柱子较矮的那个柱子的高度减去当前柱子的高度
for (int i = 1; i < n - 1; i++) {
res += Math.min(l_max[i], r_max[i]) - height[i];
}
return res;
}
}
解法三:三指针
class Solution {
public int trap(int[] height) {
// 1根柱子没法接水
// 2根柱子连在一起也没法接水
if (nums.length <= 2) {
return 0;
}
int n = nums.length;
int max = Integer.MIN_VALUE;
int maxIndex = -1;
// 找到最高的柱子
for (int i = 0; i < n; i++) {
if (height[i] > max) {
max = height[i];
maxIndex = i;
}
}
// 先让left指针指向最左边
int left = height[0];
int right = 0;
int warter = 0;
for (int i = 1; i < maxIndex; i++) {
right = height[i];
if (left > right) {
warter = water + left - right;
} else {
// 当left柱子小于等于right柱子时, left = right。
left = right;
}
}
// 先让right指针指向最右边
right = height[height.length - 1];
for (int i = height.length - 2; i > maxIndex; i--) {
left = height[i];
if (left < right) {
water = water + right - left;
} else {
right = left;
}
}
return water;
}
}
解法四:双指针
class Solution {
public int trap(int[] height) {
int n = height.length;
int left = 0, right = n - 1;
int l_max = 0, r_max = 0;
int res = 0;
while (left < right) {
// 记录height[0, left]的最大高度
l_max = Math.max(l_max, height[left]);
// 记录height[right, n]的最大高度
r_max = Math.max(r_max, height[right]);
// 左边最大值更小,计算此时左边left位置能装的水。
if (l_max < r_max) {
res += l_max - height[left];
left++;
} else {
res += r_max - height[right];
right--;
}
}
return res;
}
}
125. 验证回文串
给定一个字符串,验证它是否是回文串,只考虑字母和数字字符,可以忽略字母的大小写。
说明:本题中,我们将空字符串定义为有效的回文串。
/**
* 这道题我看主要是考察API的使用
* 1、Character.isLetterOrDigit(char ch)判断ch是否是字母或者数字;
* 2、Character.toLowerCase(char ch)将字母大写转小写。
*/
class Solution {
public boolean isPalindrome(String s) {
int n = s.length();
int left = 0, right = n - 1;
while (left < right) {
while (left < right && !Character.isLetterOrDigit(s.charAt(left))) {
left++;
}
while (left < right && !Character.isLetterOrDigit(s.charAt(right))) {
right--;
}
if (left < right) {
if (Character.toLowerCase(s.charAt(left)) != Character.toLowerCase(s.charAt(right))) {
return false;
}
left++;
right--;
}
}
return true;
}
}
167. 两数之和 II - 输入有序数组
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分
别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 < index2 <= numbers.length 。
以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
你所设计的解决方案必须只使用常量级的额外空间。
输入:numbers = [2,7,11,15], target = 9
输出:[1,2]
解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
class Solution {
public int[] twoSum(int[] nums, int target) {
// 一左一右两个指针相向而行
int left = 0, right = nums.length - 1;
// 因为题目说了index1 < index2
while (left < right) {
int sum = nums[left] + nums[right];
if (sum == target) {
// 题目要求的索引是从 1 开始的
return new int[]{left + 1, right + 1};
} else if (sum < target) {
left++; // 让 sum 大一点
} else if (sum > target) {
right--; // 让 sum 小一点
}
}
return new int[]{-1, -1};
}
}
345. 反转字符串中的元音字母
给你一个字符串 s ,仅反转字符串中的所有元音字母,并返回结果字符串。
元音字母包括 'a'、'e'、'i'、'o'、'u',且可能以大小写两种形式出现。
class Solution {
public String reverseVowels(String s) {
int i = 0, j = s.length() - 1;
char[] chars = s.toCharArray();
HashSet set = new HashSet();
set.add('a');
set.add('e');
set.add('i');
set.add('o');
set.add('u');
set.add('A');
set.add('E');
set.add('I');
set.add('O');
set.add('U');
while (i < j) {
while (i < j && !set.contains(s.charAt(i))) {
i++;
}
while (i < j && !set.contains(s.charAt(j))) {
j--;
}
char temp = chars[i];
chars[i] = chars[j];
chars[j] = temp;
i++;
j--;
}
return String.valueOf(chars);
}
}
350. 两个数组的交集 II
给你两个整数数组 nums1 和 nums2 ,请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数,应与元素在两个数组中都出现的次数一致(如果出
现次数不一致,则考虑取较小值)。可以不考虑输出结果的顺序。
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2,2]
我们可以先将数组排序,方便我们查找,然后正式流程如下:
- 创建一个指针 i 指向 nums1 数组首位,指针 j 指向 nums2 数组首位;
- 创建一个临时栈,用于存放结果集;
- 开始比较指针 i 和指针 j 的值大小,若两个值不等,则数字小的指针,往右移一位;
- 若指针 i 和指针 j 的值相等,则将交集压入栈;
- 若 nums 或 nums2 有一方遍历结束,代表另一方的剩余值,都是唯一存在,且不会与之产生交集的。
class Solution {
public int[] intersect(int[] nums1, int[] nums2) {
Arrays.sort(nums1);
Arrays.sort(nums2);
int len1 = nums1.length;
int len2 = nums2.length;
int[] intersection = new int[Math.min(len1, len2)];
int i = 0, j = 0, index = 0;
// 若nums1或nums2有一方遍历结束,代表另一方的剩余值,都是唯一存在,且不会与之产生交集的。
while (i < len1 && j < len2) {
if (nums1[i] < nums2[j]) {
i++;
} else if (nums1[i] > nums2[j]) {
j++;
} else {
intersection[index] = nums1[i];
index++;
i++;
j++;
}
}
return Arrays.copyOfRange(intersection, 0, index);
}
}
581. 最短无序连续子数组的长度⭐⭐⭐
给你一个整数数组 nums ,你需要找出一个 连续子数组 ,如果对这个子数组进行升序排序,那么整个数组都会变为升序排序。
请你找出符合题意的 最短 子数组,并输出它的长度。
最终目的是让整个数组有序,那么我们可以先将数组拷贝一份进行排序,然后使用两个指针 i 和 j 分别找到左右两端第一个不同的地方。
那么 [i, j]这一区间即是答案。
class Solution {
public int findUnsortedSubarray(int[] nums) {
int len = nums.length;
int[] arr = nums.clone();
Arrays.sort(arr);
int i = 0, j = len - 1;
while (i <= j && nums[i] == arr[i]) {
i++;
}
while (i <= j && nums[j] == arr[j]) {
j--;
}
return j - i + 1;
}
}
解析题目要求, 我们可以知道, 要求的子数组需要满足的特征:
- 子数组左边的所有元素,值都要比子数组的最小元素要小;
- 子数组右边的所有元素,值都要比子数组的最大元素要大。
从左到右遍历,,只要碰到比已经遍历过路径内的最大值要小的元素,则说明该元素需要被纳入到重排序的子数组中;
同理,再从右往左遍历,只要碰到比已经遍历过的路径内的最小值还要大的元素,说明该元素也需要被纳入到重排序的子数组中。
class Solution {
public int findUnsortedSubarray(int[] nums) {
// 双指针: 需要分别确认左右边界:
int left = 0, right = 0; //目标区域的左右边界
int max = left; // 区域内的最大值的角标
for (int i = 1; i < nums.length; i++) {
if (nums[i] >= nums[max]) {
max = i;
} else if (nums[i] < nums[max]) {
// 从左到右遍历,只要碰到比已经遍历过路径内的最大值要小的元素。
// 说明该元素需要被纳入到重排序的子数组中。
right = i;
}
}
int min = right; // 区域内的最小值的角标
for (int i = right - 1; i >= 0; i--) {
if (nums[i] <= nums[min]) {
min = i;
} else if (nums[i] > nums[min]) {
left = i;
}
}
return right == left ? 0 : right - left + 1;
}
}
快慢指针
19. 删除链表的倒数第 N 个结点
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode(0);
dummy.next = head;
// 从dummy开始移动,如果直接从head开始移动,当只有一个节点时,会报空指针异常。
ListNode fast = dummy;
ListNode slow = dummy;
// 快指针先移动n步
while (n > 0) {
fast = fast.next;
n--;
}
ListNode prev = null;
while (fast != null) {
prev = slow;
// 快慢指针同时移动,当fast指针指向null时,slow指针指向的就是要删除的节点。
// 而此时prev指针就是删除节点的前一个节点。
slow = slow.next;
fast = fast.next;
}
prev.next = slow.next;
slow.next = null;
return dummy.next;
}
}
141. 环形链表
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链
表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。

class Solution {
public boolean hasCycle(ListNode head) {
if (head == null) {
return false;
}
ListNode slow = head;
ListNode fast = head;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
if (slow == fast) {
return true;
}
}
return fasle;
}
}
202. 快乐数
class Solution {
public int getNext(int n) {
int totalSum = 0;
while (n > 0) {
int d = n % 10;
n = n / 10;
totalSum += d * d;
}
return totalSum;
}
public boolean isHappy(int n) {
int slowRunner = n;
int fastRunner = getNext(n);
while (fastRunner != 1 && slowRunner != fastRunner) {
slowRunner = getNext(slowRunner);
fastRunner = getNext(getNext(fastRunner));
}
return fastRunner == 1;
}
}
Hash
3. 无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
class Solution {
public int lengthOfLongestSubstring(String s) {
// 定义返回的最大长度,左右指针。
int Max = 0, left = 0, right = 0;
char[] charArray = s.toCharArray();
// 用Set来去重
Set<Character> set = new HashSet<>();
for (int i = 0; i < s.length(); i++) {
// 如果当前字母加入窗口中会造成重复,则不断移动左指针直到没有重复字母为止。
while (set.contains(charArray[i])) {
set.remove(charArray[left++]);
}
// 当不会造成重复时加入
set.add(charArray[i]);
int tempLen = right - left + 1;
// right 指针右移
right++;
// 尝试更新最大值
Max = Math.max(tempLen, Max);
}
return Max;
}
}
13. 罗马数字转整数
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
class Solution {
public int romanToInt(String s) {
HashMap<String, Integer> map = new HashMap<>();
map.put("I", 1);
map.put("IV", 4);
map.put("V", 5);
map.put("IX", 9);
map.put("X", 10);
map.put("XL", 40);
map.put("L", 50);
map.put("XC", 90);
map.put("C", 100);
map.put("CD", 400);
map.put("D", 500);
map.put("CM", 900);
map.put("M", 1000);
int res = 0;
for (int i = 0; i < s.length();) {
if (i + 1 < s.length() && map.containsKey(s.substring(i, i + 2))) {
res = res + map.get(s.substring(i, i + 2));
i = i + 2;
} else {
res = res + map.get(s.substring(i, i + 1));
i += 1;
}
}
return res;
}
}
36. 有效的数独⭐⭐⭐
请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
- 数字 1-9 在每一行只能出现一次。
- 数字 1-9 在每一列只能出现一次。
- 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
注意:
- 一个有效的数独(部分已被填充)不一定是可解的;
- 只需要根据以上规则,验证已经填入的数字是否有效即可;
- 空白格用 '.' 表示。
class Solution {
public boolean isValidSudoku(char[][] board) {
Map<Integer, Set<Integer>> row = new HashMap<>(), col = new HashMap<>(), area = new HashMap<>();
for (int i = 0; i < 9; i++) {
row.put(i, new HashSet<>());
col.put(i, new HashSet<>());
area.put(i, new HashSet<>());
}
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
char c = board[i][j];
if (c == '.') {
continue;
}
int u = c - '0';
// 确定这个数属于哪一个小方格
int idx = (i / 3) * 3 + j / 3;
// 判断遍历到的这个数所在的行和列之前是否出现过这个数,或者小方格是否存在这个数。
if (row.get(i).contains(u) || col.get(j).contains(u) || area.get(idx).contains(u)) {
return false;
}
row.get(i).add(u);
col.get(j).add(u);
area.get(idx).add(u);
}
}
return true;
}
}
// @solution-sync:end
class Main {
public static void main(String[] args) {
char[][] board = new char[][]{
new char[]{'5', '3', '.', '.', '7', '.', '.', '.', '.'},
new char[]{'6', '.', '.', '1', '9', '5', '.', '.', '.'},
new char[]{'.', '9', '8', '.', '.', '.', '.', '6', '.'},
new char[]{'8', '.', '.', '.', '6', '.', '.', '.', '3'},
new char[]{'4', '.', '.', '8', '.', '3', '.', '.', '1'},
new char[]{'7', '.', '.', '.', '2', '.', '.', '.', '6'},
new char[]{'.', '6', '.', '.', '.', '.', '2', '8', '.'},
new char[]{'.', '.', '.', '4', '1', '9', '.', '.', '5'},
new char[]{'.', '.', '.', '.', '8', '.', '.', '7', '9'}
};
boolean result = new Solution().isValidSudoku(board);
System.out.println(result);
}
}
128. 最长连续序列⭐⭐
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
核心思路:
如果我们知道了每一个连续序列的左边界,并且知道以它为左边界的连续序列的长度。进而就可以知道所有连续序列的长度。在其中取最大值即为结果。
但都有哪些数可以成为连续序列的左边界呢?
设想,如果num为一个左边界,那么num - 1就不应该存在于数组中(因为如果num - 1存在于数组中,num - 1又与num连续,所以num不可能是连续序列的左边
界)。因此如果一个数字num满足:num - 1不存在于数组中。这个数字num就可以成为连续序列的左边界。
具体的算法流程如下;
准备一个HashSet,将所有元素入set,之后遍历数组中的每一个数num;
如果num - 1存在于set中,那么num不可能是左边界,直接跳过;
如果num - 1不存在于set中,那么num会是一个左边界,我们再不断地查找num+1、num+2......是否存在于set中,来看以num为左边界的连续序列能有多长;
在上述遍历中,我们知道了对于每一个可能的左边界,能扩出的最长连续序列的长度,再在这些长度中取最大即为结果。
class Solution {
public int longestConsecutive(int[] nums) {
Set<Integer> set = new HashSet<>();
for (int num : nums) {
set.add(num);
}
int res = 0;
for (int num : nums) {
// 如果num - 1存在于集合中,说明num不是左边界。
if (set.contains(num - 1)) {
continue;
} else {
int len = 0;
// 一直加大num值,看集合中是否存在。
while (set.contains(num++)) {
len++;
}
res = Math.max(res, len);
}
}
return res;
}
}
202. 快乐数⭐
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。
解题思路:注意题目说的无限循环,就是说每个位置上的数字的平方和,曾经出现过,那么这样就出现了无限循环,不是快乐数了。
class Solution {
public boolean isHappy(int n) {
Set<Integer> record = new HashSet<>();
// 退出循环的两种条件是
// 1、当n == 1时,说明是快乐数
// 2、当set集合中存在这个数时,说明出现了无限循环,不是快乐数
while (n != 1 && !record.contains(n)) {
record.add(n);
n = getNextNumber(n);
}
// 比较n是不是1
return n == 1;
}
private int getNextNumber(int n) {
int res = 0;
while (n > 0) {
int temp = n % 10;
res += temp * temp;
n = n / 10;
}
return res;
}
}
49. 字母异位词分组⭐
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的字母得到的一个新单词,所有源单词中的字母通常恰好只用一次。
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]
class Solution {
public List<List<String>> groupAnagrams(String[] strs) {
HashMap<String, List<String>> map = new HashMap<>();
for (String s : strs) {
char[] chars = s.toCharArray();
// 将字符数组按字符排序
// 字母异位词排序后字符顺序就是一样的了
// 毕竟字母异位词只是字符顺序不一样,每种字符的个数是一样的。
Arrays.sort(chars);
// 这个API都有的嘛,将字符数组转换为字符串。
String str = String.valueOf(chars);
if (!map.containsKey(str)) {
map.put(str, new ArrayList<>());
}
map.get(str).add(s);
}
return new ArrayList<>(map.values());
}
}
// 对字符串排序可以是一种编码方案,如果是异位词,排序后就变成一样的了,但是这样时间复杂度略高,且会修改原始数据。
// 更好的编码方案是利用每个字符的出现次数进行编码,也就是下面的解法代码。
class Solution {
public List<List<String>> groupAnagrams(String[] strs) {
// 编码到分组的映射
HashMap<String, List<String>> codeToGroup = new HashMap<>();
for (String s : strs) {
// 对字符串进行编码
String code = encode(s);
// 把编码相同的字符串放在一起
codeToGroup.putIfAbsent(code, new LinkedList<>());
codeToGroup.get(code).add(s);
}
// 获取结果
List<List<String>> res = new LinkedList<>();
for (List<String> group : codeToGroup.values()) {
res.add(group);
}
return res;
}
// 利用每个字符的出现次数进行编码
String encode(String s) {
char[] count = new char[26];
for (char c : s.toCharArray()) {
int delta = c - 'a';
count[delta]++;
}
return new String(count);
}
}
242. 有效的字母异位词
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。
class Solution {
public boolean isAnagram(String s, String t) {
int[] record = new int[26];
for (char ch : s.toCharArray()) {
record[ch - 'a']++;
}
for (char ch : t.toCharArray()) {
record[ch - 'a']--;
}
for (int num : nums) {
if (num != 0) {
return false;
}
}
return true;
}
}
720. 词典中最长的单词⭐⭐
给出一个字符串数组 words 组成的一本英语词典。返回 words 中最长的一个单词,该单词是由 words 词典中其他单词逐步添加一个字母组成。
若其中有多个可行的答案,则返回答案中字典序最小的单词。若无答案,则返回空字符串。
输入:words = ["a", "banana", "app", "appl", "ap", "apply", "apple"]
输出:"apple"
解释:"apply" 和 "apple" 都能由词典中的单词组成。但是 "apple" 的字典序小于 "apply"
class Solution {
public String longestWord(String[] words) {
Set<String> set = new HashSet<>(Arrays.asList(words));
String ans = "";
out:
for (String word : words) {
for (int i = 1; i < word.length(); i++) {
// 如果word中的某一个前缀不存在于词典中直接跳过去处理下一个word。
if (!set.contains(word.substring(0, i))) {
continue out;
}
}
// 来到这里说明word这个字符的所有前缀都在字典中,
// 选择符合条件并且长度更长的word。
if (word.length() > ans.length()) {
ans = word;
} else if (word.length() == ans.length()) {
// 长度相同比较字典序
if (word.compareTo(ans) < 0) {
ans = word;
}
}
}
return ans;
}
}
class Main {
public static void main(String[] args) {
String[] words = new String[]{"w", "wo", "wor", "worl", "world"};
String result = new Solution().longestWord(words);
System.out.println(result);
}
}
N数之和
我先来编一道 twoSum 题目:
如果假设输入一个数组 nums 和一个目标和 target,请你返回 nums 中能够凑出 target 的两个元素的值,比如输入 nums = [1,3,5,6], target = 9,那么
算法返回两个元素 [3,6]。可以假设只有且仅有一对儿元素可以凑出 target。
我们可以先对 nums 排序,然后利用前文 双指针技巧 写过的左右双指针技巧,从两端相向而行就行了:
int[] twoSum(int[] nums, int target) {
// 先对数组排序
Arrays.sort(nums);
// 左右指针
int lo = 0, hi = nums.size() - 1;
while (lo < hi) {
int sum = nums[lo] + nums[hi];
// 根据 sum 和 target 的比较,移动左右指针
if (sum < target) {
lo++;
} else if (sum > target) {
hi--;
} else if (sum == target) {
return {nums[lo], nums[hi]};
}
}
return {};
}
这样就可以解决这个问题,力扣第 1 题「两数之和」和力扣第 167 题「两数之和 II - 输入有序数组」稍加修改就可以用类似的思路解决,我这里就不写了。
不过我要继续魔改题目,把这个题目变得更泛化,更困难一点:
nums 中可能有多对儿元素之和都等于 target,请你的算法返回所有和为 target 的元素对儿,其中不能出现重复。
int[][] twoSumTarget(int[] nums, int target);
比如说输入为 nums = [1,3,1,2,2,3], target = 4,那么算法返回的结果就是:[[1,3],[2,2]](注意,我要求返回元素,而不是索引)。
对于修改后的问题,关键难点是现在可能有多个和为 target 的数对儿,还不能重复,比如上述例子中 [1,3] 和 [3,1] 就算重复,只能算一次。
首先,基本思路肯定还是排序加双指针:
vector<vector<int>> twoSumTarget(vector<int>& nums, int target) {
// 先对数组排序
sort(nums.begin(), nums.end());
vector<vector<int>> res;
int lo = 0, hi = nums.size() - 1;
while (lo < hi) {
int sum = nums[lo] + nums[hi];
// 根据 sum 和 target 的比较,移动左右指针
if (sum < target) lo++;
else if (sum > target) hi--;
else {
res.push_back({nums[lo], nums[hi]});
lo++; hi--;
}
}
return res;
}
但是,这样实现会造成重复的结果,比如说 nums = [1,1,1,2,2,3,3], target = 4,得到的结果中 [1,3] 肯定会重复。
出问题的地方在于 sum == target 条件的 if 分支,当给 res 加入一次结果后,lo 和 hi 不仅应该相向而行,而且应该跳过所有重复的元素:
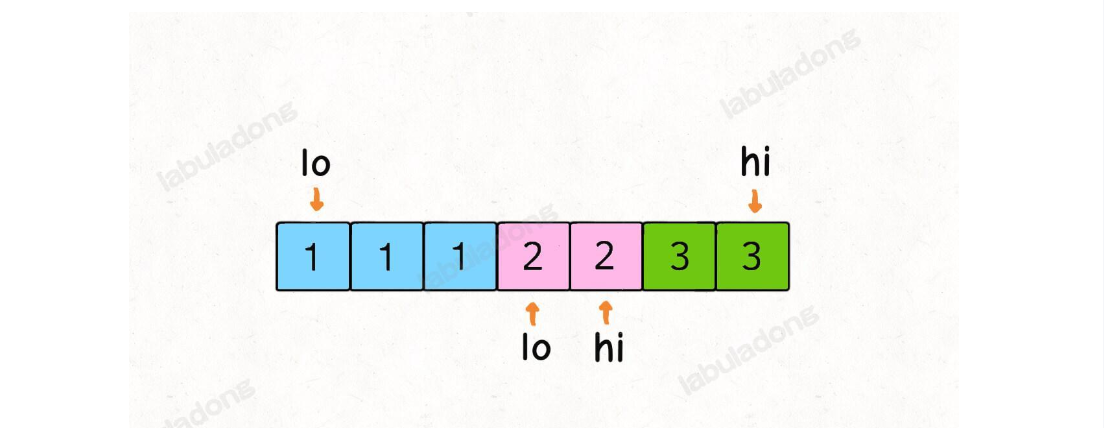
所以,可以对双指针的 while 循环做出如下修改:
while (lo < hi) {
int sum = nums[lo] + nums[hi];
// 记录索引 lo 和 hi 最初对应的值
int left = nums[lo], right = nums[hi];
if (sum < target) lo++;
else if (sum > target) hi--;
else {
res.push_back({left, right});
// 跳过所有重复的元素
while (lo < hi && nums[lo] == left) lo++;
while (lo < hi && nums[hi] == right) hi--;
}
}
这样就可以保证一个答案只被添加一次,重复的结果都会被跳过,可以得到正确的答案。不过,受这个思路的启发,其实前两个 if 分支也是可以做一点效率优化,
跳过相同的元素:
public List<List<Integer>> twoSum(int[] nums, int target) {
// 数组需要排序
Arrays.sort(nums);
// 存储结果
List<List<Integer>> res = new ArrayList<>();
// 注意开闭,全闭区间
int lo = 0, hi = nums.length - 1;
// 结束条件:lo == hi
while (lo < hi) {
int left = nums[lo], right = nums[hi];
int sum = left + right;
if (sum < target) {
// 排除重复元素
while (lo < hi && left == nums[lo]) lo++;
} else if (sum > target) {
// 排除重复元素
while (lo < hi && right == nums[hi]) hi--;
} else {
List<Integer> list = new ArrayList<>();
list.add(left);
list.add(right);
res.add(list);
// 排除重复元素
while (lo < hi && left == nums[lo]) lo++;
while (lo < hi && right == nums[hi]) hi--;
}
}
return res;
}
「三数和」利用「二数和」,即:确定一个数,就变成了「二数和」
public List<List<Integer>> threeSum(int[] nums) {
// 排序
Arrays.sort(nums);
List<List<Integer>> res = new ArrayList<>();
for (int i = 0; i < nums.length; i++) {
// 确定 num[i],从 i + 1 开始寻找「二数和」
List<List<Integer>> twoSumList = twoSum(nums, i + 1, 0 - nums[i]);
// 结果汇合
for (List<Integer> list : twoSumList) {
list.add(nums[i]);
res.add(list);
}
// 排除重复元素
while (i < nums.length - 1 && nums[i] == nums[i + 1]) i++;
}
return res;
}
// start : 开始下标,不再从 0 开始
private List<List<Integer>> twoSum(int[] nums, int start, int target) {
List<List<Integer>> res = new ArrayList<>();
int lo = start, hi = nums.length - 1;
while (lo < hi) {
int left = nums[lo], right = nums[hi];
int sum = left + right;
if (sum < target) {
while (lo < hi && left == nums[lo]) lo++;
} else if (sum > target) {
while (lo < hi && right == nums[hi]) hi--;
} else {
List<Integer> list = new ArrayList<>();
list.add(left);
list.add(right);
res.add(list);
while (lo < hi && left == nums[lo]) lo++;
while (lo < hi && right == nums[hi]) hi--;
}
}
return res;
}
「四数和」利用「三数和」,即:确定一个数,就变成了「三数和」
public List<List<Integer>> fourSum(int[] nums, int target) {
// 排序
Arrays.sort(nums);
List<List<Integer>> res = new ArrayList<>();
for (int i = 0; i < nums.length; i++) {
// 确定 num[i],从 i + 1 开始寻找「三数和」
List<List<Integer>> threeSumList = threeSum(nums, i + 1, target - nums[i]);
for (List<Integer> list : threeSumList) {
list.add(nums[i]);
res.add(list);
}
// 排除重复元素
while (i < nums.length - 1 && nums[i] == nums[i + 1]) i++;
}
return res;
}
// start : 开始下标,不再从 0 开始
private List<List<Integer>> threeSum(int[] nums, int start, int target) {
List<List<Integer>> res = new ArrayList<>();
for (int i = start; i < nums.length; i++) {
List<List<Integer>> twoSumList = twoSum(nums, i + 1, target - nums[i]);
for (List<Integer> list : twoSumList) {
list.add(nums[i]);
res.add(list);
}
while (i < nums.length - 1 && nums[i] == nums[i + 1]) i++;
}
return res;
}
private List<List<Integer>> twoSum(int[] nums, int start, int target) {
List<List<Integer>> res = new ArrayList<>();
int lo = start, hi = nums.length - 1;
while (lo < hi) {
int left = nums[lo], right = nums[hi];
int sum = left + right;
if (sum < target) {
while (lo < hi && left == nums[lo]) lo++;
} else if (sum > target) {
while (lo < hi && right == nums[hi]) hi--;
} else {
List<Integer> list = new ArrayList<>();
list.add(left);
list.add(right);
res.add(list);
while (lo < hi && left == nums[lo]) lo++;
while (lo < hi && right == nums[hi]) hi--;
}
}
return res;
}
看了上面的「二数和」「三数和」「四数和」,是否有一种无限套娃的感觉
现在将上面的代码重构,变成 N 数和。
// nums : 有序数组
// start : 开始下标
// target : 目标数
// k : 数量
public List<List<Integer>> nSum(int[] nums, int start, int target, int k) {
int n = nums.length;
List<List<Integer>> res = new ArrayList<>();
// k > 2 : 递归调用 k - 1 k -2 k - 3
if (k > 2) {
for (int i = start; i < n; i++) {
List<List<Integer>> sumList = nSum(nums, i + 1, target - nums[i], k - 1);
for (List<Integer> list : sumList) {
list.add(nums[i]);
res.add(list);
}
while (i < n - 1 && nums[i] == nums[i + 1]) i++;
}
} else {
// k = 2 : 使用「二数和」
int lo = start, hi = n - 1;
while (lo < hi) {
int left = nums[lo], right = nums[hi];
int sum = left + right;
if (sum < target) {
while (lo < hi && left == nums[lo]) lo++;
} else if(sum > target) {
while (lo < hi && right == nums[hi]) hi--;
} else {
List<Integer> list = new ArrayList<>();
list.add(left);
list.add(right);
res.add(list);
while (lo < hi && left == nums[lo]) lo++;
while (lo < hi && right == nums[hi]) hi--;
}
}
}
return res;
}
1. 两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
class solution {
public int twoSum(int[] nums, int target) {
int[] res = new int[2];
HashMap<Integer, Integer> map = new HashMap<>();
if (nums == null || nums.length == 0) {
return res;
}
for (int i = 0; i < nums.length; i++) {
int temp = target - nums[i];
if (map.containsKey(temp)) {
res[1] = i;
res[0] = map.get(temp);
}
// 将从nums数组中遍历到的数放在map中,key是nums[i],value是下标i。
map.put(nums[i], i);
}
return res;
}
}
2. 两数相加
给你两个非空的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
// 初始化一个第一个节点为0的链表
ListNode result = new ListNode(0);
// 把该链表的引用给临时的表示当前节点的链表 (请注意Java是赋值方式)
ListNode current = result;
// 表示余数(本题目中carry要么0,要么1, 为什么?仔细阅读题目)
int carry = 0;
// 如果任意一个链表不为null,则继续循环
while (l1 != null || l2 != null) { // 有可能两个数并不具有相同的位
// 接下来的操作就是l1当前值 + l2当前值 + 上次计算得到的carry余数
int sum = carry;
// 如果链表1不为null,即没有计算到终点,把当前值给sum, 计算完成后从链表1去掉当前节点
if (l1 != null) {
sum += l1.val;
l1 = l1.next;
}
// 如果链表2不为null,即没有计算到终点,把当前值给sum, 计算完成后从链表2去掉当前节点
if (l2 != null) {
sum += l2.val;
l2 = l2.next;
}
// 进位 前面计算值 / 10
carry = sum / 10;
// 两数的和为sum%10,即如果sum大于10,则sum为超出10的部分,也就是余数。
sum = sum % 10;
// 当前节点的下一个节点设为计算得到的sum
current.next = new ListNode(sum);
// 把上一步的节点赋给当前节点(如果不理解为什么,请用idea调试一下过程)
current = current.next;
}
// 最终计算完成了如果余数位仍然大于0(这里其实可以换成carry是否为1,如果1则下一个节点设为1)
if (carry == 1) {
current.next = new ListNode(carry);
}
// 返回result,因为result链表的第一个节点为0(初始化的值),就直接返回下一个节点即可。
return result.next;
}
}
15. 三数之和
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
这道题难点在去重剪枝的操作。
class solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
// 先对数组进行排序
Arrays.sort(nums);
for (int i = 0; i < nums.length; i++) {
// 很明显当三个数中的第一个数都大于0了,三数之和肯定不会为0。
if (nums[i] > 0) {
return res;
}
// 这里去重是因为前一个数已经将后面可能和为0的数扫描过了,如果下一个数还和前一个数相同,往下执行扫描就会出现重复的结果。
// 比如-1, -1,-1, 2, 2, 2 第一个-1时就会将后面和为0的数找到了,如果还从第二个-1开始找就会出现重复的情况。
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
int left = i + 1;
int right = nums.length - 1;
while (left < right) {
int sum = nums[i] + nums[left] + nums[right];
if (sum > 0) {
right--;
} else if (sum < 0) {
left++;
} else {
res.add(Arrays.asList(nums[i], nums[left], nums[right]));
// 当找到一个和为0的三数组合时,如果nums[left] == nums[left + 1] 同时 nums[right] == nums[right - 1]
// 此时如果不剪枝就出现了重复的三数组合。 如-1, -1, -1, 2, 2, 2
while (left < right && nums[left] == nums[left + 1]) {
left++;
}
while (left < right && nums[right] == nums[right - 1]) {
right--;
}
right--;
left++;
}
}
}
return res;
}
}
// 模板解法
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
Arrays.sort(nums);
int n = nums.length;
for (int i = 0; i < n; i++) {
ArrayList<ArrayList<Integer>> tuples = twoSumTarget(nums, i + 1, 0 - nums[i]);
for (List<Integer> list : tuples) {
list.add(nums[i]);
res.add(list);
}
// 不让第一个数重复至于后面的两个数,我们复用的 twoSum 函数会保证它们不重复。
// 所以代码中必须用一个 while 循环来保证 3Sum 中第一个元素不重复。
while (i < n - 1 && nums[i] == nums[i + 1]) {
i++;
}
}
return res;
}
ArrayList<ArrayList<Integer>> twoSumTarget(int[] nums, int start, int target) {
ArrayList<ArrayList<Integer>> res = new ArrayList<>();
Arrays.sort(nums);
int lo = start, hi = nums.length - 1;
while (lo < hi) {
int sum = nums[lo] + nums[hi];
int left = nums[lo];
int right = nums[hi];
// 去重
if (sum < target) {
while (lo < hi && nums[lo] == left) {
lo++;
}
} else if (sum > target) {
while (lo < hi && nums[hi] == right) {
hi--;
}
} else {
ArrayList<Integer> list = new ArrayList();
list.add(left);
list.add(right);
res.add(list);
while (lo < hi && nums[lo] == left) {
lo++;
}
while (lo < hi && nums[hi] == right) {
hi--;
}
}
}
return res;
}
}
16. 最接近的三数之和⭐⭐⭐
给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数,使它们的和与 target 最接近。
返回这三个数的和。
假定每组输入只存在恰好一个解。
class solution {
public int threeSumClosest(int[] nums, target) {
Arrays.sort(nums);
int ans = nums[0] + nums[1] + nums[2];
for (int i = 0; i < nums.length; i++) {
int left = i + 1;
int right = nums.length - 1;
int sum = nums[i] + nums[left] + nums[right];
if (Math.abs(target - sum) < Math.abs(target - ans)) {
ans = sum;
}
if (sum < target) {
left++;
} else if (sum > target) {
right--;
} else {
return ans;
}
}
return ans;
}
}
18. 四数之和
给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a],nums[b],nums[c],nums[d]]
若两个四元组元素一一对应,则认为两个四元组重复:
- 0 <= a, b, c, d < n,a、b、c 和 d 互不相同;
- nums[a] + nums[b] + nums[c] + nums[d] == target。
你可以按任意顺序返回答案。
这道题是在一个数组中找到4个数之和等于target的全部四元组。
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> res = new ArrayList<>();
Arrays.sort(nums);
for (int i = 0; i < nums.length; i++) {
// 去重
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
// 去重
for (int j = i + 1; j < nums.length - 2; j++) {
if (j > i + 1 && nums[j] == nums[j - 1]) {
continue;
}
int left = j + 1;
int right = nums.length - 1;
while (left < right) {
long sum = nums[i] * 1l + nums[j] + nums[left] + nums[right];
if (sum > target) {
right--;
} else if (sum < target) {
left++;
} else {
res.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));
// 去重
while (right > left && nums[right] == nums[right - 1]) {
right--;
}
// 去重
while (right > left && nums[left] == nums[left + 1]) {
left++;
}
left++;
right--;
}
}
}
}
return res;
}
}
// 模板写法
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
Arrays.sort(nums);
List<List<Integer>> res = nSumTarget(nums, 4, 0, target);
return res;
}
public List<List<Integer>> nSumTarget(int[] nums, int n, int start, int target) {
int sz = nums.length;
List<List<Integer>> res = new ArrayList<>();
if (n < 2 || sz < n) {
return res;
}
if (n == 2) {
int lo = start, hi = sz - 1;
while (lo < hi) {
int sum = nums[lo] + nums[hi];
int left = nums[lo], right = nums[hi];
if (sum < target) {
while (lo < hi && nums[lo] == left) {
lo++;
}
} else if (sum > target) {
while (lo < hi && nums[hi] == right) {
hi--;
}
} else {
ArrayList<Integer> list = new ArrayList<>();
list.add(left);
list.add(right);
res.add(list);
while (lo < hi && nums[lo] == left) {
lo++;
}
while (lo < hi && nums[hi] == right) {
right--;
}
}
}
} else {
for (int i = start; i < sz; i++) {
List<List<Integer>> sub = nSumTarget(nums, n - 1, i + 1, target - nums[i]);
for (List<Integer> list : sub) {
ArrayList array = new ArrayList();
list.add(nums[i]);
for (Integer num : list) {
array.add(num);
}
res.add(array);
}
while (i < sz - 1 && nums[i] == nums[i + 1]) {
i++;
}
}
}
return res;
}
}
454. 四数相加 II(hash)⭐⭐⭐
给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足:
- 0 <= i,j, k, l < n;
- nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0。
题目的要求是在四个数组中找到和为0的四个数的组合。
思路就是先
class Solution {
public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
Map<Integer, Integer> map = new HashMap<>();
int temp;
int res = 0;
// 统计两个数组中的元素之和,同时统计出现的次数,放入map
for (int i : nums1) {
for (int j : nums2) {
temp = i + j;
// 如果出现过就将次数加一
if (map.containsKey(temp)) {
map.put(temp, map.get(temp) + 1);
} else {
// map中没有出现过直接放入map
map.put(temp, 1);
}
}
}
// 统计剩余的两个元素的和,在map中找是否存在相加为0的情况,同时记录次数
for (int i : nums3) {
for (int j : nums4) {
temp = i + j;
if (map.containsKey(0 - temp)) {
res += map.get(0 - temp);
}
}
}
return res;
}
}
二分
二分查找并不简单,Knuth 大佬(发明 KMP 算法的那位)都说二分查找:思路很简单,细节是魔鬼。很多人喜欢拿整型溢出的 bug 说事儿,但是二分查找真正的
坑根本就不是那个细节问题,而是在于到底要给 mid 加一还是减一,while 里到底用 <= 还是 <。
你要是没有正确理解这些细节,写二分肯定就是玄学编程,有没有 bug 只能靠菩萨保佑(谁写谁知道)。
普通二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
class Solution {
public int search(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] > target) {
right = mid - 1; // 左闭
} else if (nums[mid] < target) {
left = mid + 1; // 右闭
} else {
return mid; // 返回下标
}
}
return -1;
}
}
寻找左侧边界的二分查找
class Solution {
public int leftBound(int[] nums, int target) {
int left = 0;
int right = nums.length;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
// 若target比nums数组中所有的数都大一直递增直到left == right == nums.length退出
// 此时数组中不存在这个数返回-1。
// 那要是target比数组中所有元素都小呢?
// 因为我们搜索的区间是左闭右开的,right一直减到left==0此时在判断nums[left] == target就可以直到target不在数组中
if (left = nums.length) {
return -1;
}
// 判断target是否在数组中。
return nums[left] == target ? left : -1;
}
}
能不能想办法把 right 变成 nums.length - 1,也就是继续使用两边都闭的「搜索区间」?这样就可以和第一种二分搜索在某种程度上统一起来了。
答:当然可以,只要你明白了「搜索区间」这个概念,就能有效避免漏掉元素,随便你怎么改都行。下面我们严格根据逻辑来修改:
因为你非要让搜索区间两端都闭,所以 right 应该初始化为 nums.length - 1,while 的终止条件应该是 left == right + 1,也就是其中应该用 <=:
int leftBound(int[] nums, int target) {
// 搜索区间为 [left, right]
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
// if else ...
}
因为搜索区间是两端都闭的,且现在是搜索左侧边界,所以 left 和 right 的更新逻辑如下:
if (nums[mid] < target) {
// 搜索区间变为 [mid+1, right]
left = mid + 1;
} else if (nums[mid] > target) {
// 搜索区间变为 [left, mid-1]
right = mid - 1;
} else if (nums[mid] == target) {
// 收缩右侧边界
right = mid - 1;
}
和刚才相同,如果想在找不到 target 的时候返回 -1,那么检查一下 nums[left] 和 target 是否相等即可:
// 此时 target 比所有数都大,返回 -1
if (left == nums.length) return -1;
// 判断一下 nums[left] 是不是 target
return nums[left] == target ? left : -1;
至此,整个算法就写完了,完整代码如下:
int leftBound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
// 搜索区间为 [left, right]
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
// 搜索区间变为 [mid+1, right]
left = mid + 1;
} else if (nums[mid] > target) {
// 搜索区间变为 [left, mid-1]
right = mid - 1;
} else if (nums[mid] == target) {
// 收缩右侧边界
right = mid - 1;
}
}
// 判断 target 是否存在于 nums 中
// 此时 target 比所有数都大,返回 -1
if (left == nums.length) {
return -1;
}
// 判断一下 nums[left] 是不是 target
return nums[left] == target ? left : -1;
}
寻找右侧边界的二分查找
class Solution {
public int rightBound(int[] nums, int target) {
int left = 0;
int right = nums.length;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
left = mid + 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
// 判断 target 是否存在于 nums 中
// 此时 left - 1 索引越界
if (left - 1 < 0) return -1;
// 判断一下 nums[left] 是不是 target
return nums[left - 1] == target ? (left - 1) : -1;
}
}
是否也可以把这个算法的「搜索区间」也统一成两端都闭的形式呢?这样这三个写法就完全统一了,以后就可以闭着眼睛写出来了。
答:当然可以,类似搜索左侧边界的统一写法,其实只要改两个地方就行了:
class Solution {
public int rightBound(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] == taget) {
left = mid + 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > taget) {
right = mid - 1;
}
}
// 判断 target 是否存在于 nums 中
// 此时 left - 1 索引越界
if (left - 1 < 0) return -1;
// 判断一下 nums[left] 是不是 target
return nums[left - 1] == target ? (left - 1) : -1;
}
}
当然,由于 while 的结束条件为 right == left - 1,所以你把上述代码中的 left - 1 都改成 right 也没有问题,这样可能更有利于看出来这是在「搜索右
侧边界」。至此,搜索右侧边界的二分查找的两种写法也完成了,其实将「搜索区间」统一成两端都闭反而更容易记忆,你说是吧?
逻辑统一二分查找
int binarySearch(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while(left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if(nums[mid] == target) {
// 直接返回
return mid;
}
}
// 直接返回
return -1;
}
int leftBound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回,锁定左侧边界
right = mid - 1;
}
}
// 判断 target 是否存在于 nums 中
// 此时 target 比所有数都大,返回 -1
if (left == nums.length) return -1;
// 判断一下 nums[left] 是不是 target
return nums[left] == target ? left : -1;
}
int rightBound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回,锁定右侧边界
left = mid + 1;
}
}
// 此时 left - 1 索引越界
if (left - 1 < 0) return -1;
// 判断一下 nums[left] 是不是 target
return nums[left - 1] == target ? (left - 1) : -1;
如果以上内容你都能理解,那么恭喜你,二分查找算法的细节不过如此。通过本文,你学会了:
1、分析二分查找代码时,不要出现 else,全部展开成 else if 方便理解;
2、注意「搜索区间」和 while 的终止条件,如果存在漏掉的元素,记得在最后检查;
3、如需定义左闭右开的「搜索区间」搜索左右边界,只要在 nums[mid] == target 时做修改即可,搜索右侧时需要减一;
4、如果将「搜索区间」全都统一成两端都闭,好记,只要稍改 nums[mid] == target 条件处的代码和返回的逻辑即可,推荐拿小本本记下,作为二分搜索模板。
最后我想说,以上二分搜索的框架属于「术」的范畴,如果上升到「道」的层面,二分思维的精髓就是:通过已知信息尽可能多地收缩(折半)搜索空间,从而增
加穷举效率,快速找到目标。
二分搜索问题的泛化
什么问题可以运用二分搜索算法技巧?
首先,你要从题目中抽象出一个自变量 x,一个关于 x 的函数 f(x),以及一个目标值 target。
同时,x, f(x), target 还要满足以下条件:
1、f(x) 必须是在 x 上的单调函数(单调增单调减都可以)。
2、题目是让你计算满足约束条件 f(x) == target 时的 x 的值。
上述规则听起来有点抽象,来举个具体的例子:
给你一个升序排列的有序数组 nums 以及一个目标元素 target,请你计算 target 在数组中的索引位置,如果有多个目标元素,返回最小的索引。
这就是「搜索左侧边界」这个基本题型,解法代码之前都写了,但这里面 x, f(x), target 分别是什么呢?
我们可以把数组中元素的索引认为是自变量 x,函数关系 f(x) 就可以这样设定:
// 函数 f(x) 是关于自变量 x 的单调递增函数
// 入参 nums 是不会改变的,所以可以忽略,不算自变量
int f(int x, int[] nums) {
return nums[x];
}
其实这个函数 f 就是在访问数组 nums,因为题目给我们的数组 nums 是升序排列的,所以函数 f(x) 就是在 x 上单调递增的函数。
最后,题目让我们求什么来着?是不是让我们计算元素 target 的最左侧索引?
是不是就相当于在问我们「满足 f(x) == target 的 x 的最小值是多少」?
画个图,如下:
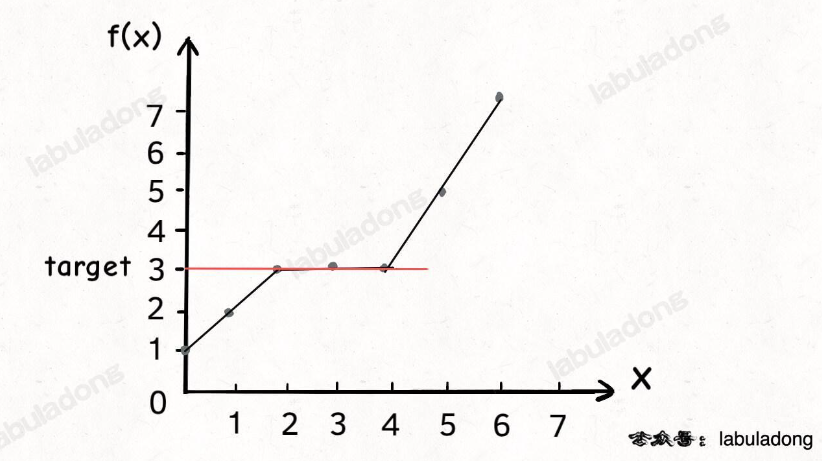
如果遇到一个算法问题,能够把它抽象成这幅图,就可以对它运用二分搜索算法。
算法代码如下:
// 函数 f 是关于自变量 x 的单调递增函数
int f(int x, int[] nums) {
return nums[x];
}
int left_bound(int[] nums, int target) {
if (nums.length == 0) return -1;
int left = 0, right = nums.length;
while (left < right) {
int mid = left + (right - left) / 2;
if (f(mid, nums) == target) {
// 当找到 target 时,收缩右侧边界
right = mid;
} else if (f(mid, nums) < target) {
left = mid + 1;
} else if (f(mid, nums) > target) {
right = mid;
}
}
return left;
}
这段代码把之前的代码微调了一下,把直接访问 nums[mid] 套了一层函数 f,其实就是多此一举,但是,这样能抽象出二分搜索思想在具体算法问题中的框架。
运用二分搜索的套路框架:
想要运用二分搜索解决具体的算法问题,可以从以下代码框架着手思考:
// 函数 f 是关于自变量 x 的单调函数
int f(int x) {
// ...
}
// 主函数,在 f(x) == target 的约束下求 x 的最值
int solution(int[] nums, int target) {
if (nums.length == 0) return -1;
// 问自己:自变量 x 的最小值是多少?
int left = ...;
// 问自己:自变量 x 的最大值是多少?
int right = ... + 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (f(mid) == target) {
// 问自己:题目是求左边界还是右边界?
// ...
} else if (f(mid) < target) {
// 问自己:怎么让 f(x) 大一点?
// ...
} else if (f(mid) > target) {
// 问自己:怎么让 f(x) 小一点?
// ...
}
}
return left;
}
具体来说,想要用二分搜索算法解决问题,分为以下几步:
1、确定 x, f(x), target 分别是什么,并写出函数 f 的代码。
2、找到 x 的取值范围作为二分搜索的搜索区间,初始化 left 和 right 变量。
3、根据题目的要求,确定应该使用搜索左侧还是搜索右侧的二分搜索算法,写出解法代码。
下面用几道例题来讲解这个流程。
875,
69. x 的平方根
题意分析
这道题要求我们实现平方根函数,输入是一个非负整数,输出也是一个整数;
但是题目当中说:结果只保留整数的部分,小数部分将被舍去。这是什么意思呢?我们分析一下示例。
示例 1:
输入: 4
输出: 2
这是显然的,4 本身是一个完全平方数,2^2 = 4 虽然在数学上一个数的平方根有正有负,但是这个题目只要求我们返回算术平方根。
示例 2 :
输入: 8
输出: 2
因为 8 的平方根实际上是 2.82842,题目要求我们将小数部分舍去。因此输出 2。于是我们知道:由于输出结果的时候,需要将小数部分舍去,因此问题的答案,
平方以后一定不会严格大于输入的整数。这里返回 3就不对了,这是因为 3^2 = 9 > 8。
思路分析
从题目的要求和示例我们可以看出,这其实是一个查找整数的问题,并且这个整数是有范围的。
-
如果这个整数的平方 恰好等于 输入整数,那么我们就找到了这个整数;
-
如果这个整数的平方 严格大于 输入整数,那么这个整数肯定不是我们要找的那个数;
-
如果这个整数的平方 严格小于 输入整数,那么这个整数 可能 是我们要找的那个数(重点理解这句话)。
因此我们可以使用「二分查找」来查找这个整数,不断缩小范围去猜。
-
猜的数平方以后大了就往小了猜;
-
猜的数平方以后恰恰好等于输入的数就找到了;
-
猜的数平方以后小了,可能猜的数就是,也可能不是。
很容易知道,题目要我们返回的整数是有范围的,直觉上一个整数的平方根肯定不会超过它自己的一半,但是 0 和 1 除外,因此我们可以在 1到输入整数除以 2 这
个范围里查找我们要找的平方根整数。0单独判断一下就好。
class Solution {
public int mySqrt(int x) {
if (x == 0 || x == 1) {
return x;
}
int left = 1;
int right = x / 2;
while (left <= right) {
int mid = left + (right - left) / 2;
if (mid > x / mid) {
right = mid - 1;
} else if (mid < x / mid) {
left = mid + 1;
} else {
return mid;
}
}
return right;
}
}
287. 寻找重复数⭐⭐⭐
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有一个重复的整数 ,返回这个重复的数 。
二分查找的思路是先猜一个数(有效范围 [left..right] 里位于中间的数 mid),然后统计原始数组中小于等于 mid 的元素的个数 cnt:
- 如果 cnt 严格大于 mid。根据抽屉原理,重复元素就在区间 [left..mid] 里;
- 否则,重复元素就在区间 [mid + 1..right] 里。
与绝大多数使用二分查找问题不同的是,这道题正着思考是容易的,即:思考哪边区间存在重复数是容易的,因为有抽屉原理做保证。
二分解法:
class Solution {
public int findDuplicate(int[] nums) {
int left = 1;
int right = nums.length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
int count = 0;
for (int num : nums) {
if (num <= mid) {
count++;
}
}
if (count > mid) {
right = mid;
} else {
left = mid + 1;
}
}
// 因为while循环时判断的是left < right,当退出循环时,left == right 这时候left和right都可以作为返回结果。
return left;
}
}
快慢指针解法:
class Solution {
public int findDuplicate(int[] nums) {
int slow = 0;
int fast = 0;
while (true) {
slow = nums[slow];
fast = nums[nums[fast]];
if (slow == fast) {
slow = 0;
while (slow != fast) {
slow = nums[slow];
fast = nums[fast];
}
return slow;
}
}
}
}
33. 搜索旋转排序数组⭐⭐⭐
整数数组 nums 按升序排列,数组中的值互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0],
nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你旋转后的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
其实题目中说「你的算法时间复杂度必须是O(logn) 级别」。提示我们可以使用二分查找算法。题目中还说「你可以假设数组中不存在重复的元素」。
根据示例 [4, 5, 6, 7, 0, 1, 2] ,自己手写几个旋转数组。不难发现:将待搜索区间从中间一分为二,位于中间的元素 nums[mid] 一定会落在其中一个有序区间里。
需要分类讨论。
这道题其实是要我们明确「二分」的本质是什么。
「二分」不是单纯指从有序数组中快速找某个数,这只是「二分」的一个应用。
「二分」的本质是两段性,并非单调性。只要一段满足某个性质,另外一段不满足某个性质,就可以用「二分」。
class Solution {
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
return mid;
}
// 举个栗子
// 3 4 5 6 7 8 9 0 1 2
// 此时属于从左边界开始递增到超过数组一半
// nums[mid] = 7
// 当 nums[mid] 在 target 的右边时 nums[mid] > target && target >= nums[left]
// 为什么还要保证 target > nums[left] 因为数组右边部分比如0 1 2 也是小于nums[mid]的
// 加上 target >= nums[left] 就把范围限制在了 nums[left] 和 nums[mid - 1] 之间
if (nums[mid] >= nums[left]) {
if (nums[mid] > target && target >= nums[left]) {
right = mid - 1;
// 当target在 8 9 中此时nums[mid] < target,又或者 target 在 0 1 2 中此时 target < nums[left]。
// 这两种情况都应该移动left指针
} else if (nums[mid] < target || target < nums[left]) {
left = mid + 1;
}
// 属于这种情况也举个例子
// 8 9 0 1 2 3 4 5 6 7
// 此时属于到数组右边界的递增长度超过了数组一半
// 此时 nums[mid] = 2 即 nums[mid] < nums[left]
// 如果 target 在 3 4 5 6 7 中 那么有 nums[mid] < target && target <= nums[right] 此时移动左边界 left = mid + 1。
} else if (nums[mid] < nums[left]) {
if (nums[mid] < target && target <= nums[right]) {
left = mid + 1;
// 如果 target 在 0 1 中 此时 nums[mid] > target,又或者 target 在 8 9 中此时 target > nums[right]。
} else if (nums[mid] > target || target > nums[right]) {
right = mid - 1;
}
}
}
return -1;
}
}
81. 搜索旋转排序数组 II⭐⭐⭐
已知存在一个按非降序排列的整数数组 nums ,数组中的值不必互不相同。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转 ,使数组变为 [nums[k], nums[k+1], ..., nums[n-1],
nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。给你 旋转后 的数组
nums 和一个整数 target ,请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ,则返回 true ,否则返回 false 。
你必须尽可能减少整个操作步骤。
解题思路:
这道题和上一道题不同的地方在于这道题的数组中存在重复元素
class Solution {
public boolean search(int[] nums, int target) {
// 左右指针
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
// 如果找到了目标值,返回其下标。
if (nums[mid] == target) {
return true;
}
// 为什么这样就去重了呢?
// 比如栗子 1 3 1 1 1 target = 3
// 当 nums[mid] >= nums[left]时,并且 target > nums[mid]。
// 此时不去重 left = mid + 1就会漏掉target。
if (nums[mid] == nums[left]) {
left++;
continue;
}
// 整个数组被划分为两部分,每一部分都是递增的。
if (nums[mid] >= nums[left]) {
if (nums[mid] > target && target >= nums[left]) {
right = mid - 1;
} else if (target > nums[mid] || target < nums[left]) {
left = mid + 1;
}
} else if (nums[mid] < nums[left]) {
if (nums[mid] < target && target <= nums[right]) {
left = mid + 1;
} else if (target < nums[mid] || target > nums[right]) {
right = mid - 1;
}
}
}
// 没有查找到
return false;
}
}
// 另外一种去重方式
class Solution {
public boolean search(int[] nums, int target) {
// 左右指针
int left = 0;
int right = nums.length - 1;
while (left <= right) {
// 这种去重方式会让左右两边各有一个相同的数 1 0 1 1 1 变为 1 0 1
// 我觉得这种去重方式不太优雅,没有严格保证二段性,让旋转点的一段严格大于另一端
while (left < right && nums[left] == nums[left + 1]) {
left++;
}
while (left < right && nums[right] == nums[right - 1]) {
right--;
}
int mid = left + (right - left) / 2;
// 如果找到了目标值,返回其下标。
if (nums[mid] == target) {
return true;
}
// 整个数组被划分为两部分,每一部分都是递增的。
if (nums[mid] >= nums[left]) {
if (nums[mid] > target && target >= nums[left]) {
right = mid - 1;
} else if (target > nums[mid] || target < nums[left]) {
left = mid + 1;
}
} else if (nums[mid] < nums[left]) {
if (nums[mid] < target && target <= nums[right]) {
left = mid + 1;
} else if (target < nums[mid] || target > nums[right]) {
right = mid - 1;
}
}
}
// 没有查找到
return false;
}
}
// 最终采取的去重方式
class Solution {
public boolean search(int[] nums, int target) {
// 左右指针
int left = 0;
int right = nums.length - 1;
while (left <= right) {
// 为什么这样就去重了呢?
// 比如栗子 1 3 1 1 1 target = 3
// 当 nums[mid] >= nums[left]时,并且 target > nums[mid]。
// 这样保证了二段性,一段严格大于另一段。
while (left < right && nums[0] == nums[right]) {
right--;
}
int mid = left + (right - left) / 2;
// 如果找到了目标值,返回其下标。
if (nums[mid] == target) {
return true;
}
// 整个数组被划分为两部分,每一部分都是递增的。
if (nums[mid] >= nums[left]) {
if (nums[mid] > target && target >= nums[left]) {
right = mid - 1;
} else if (target > nums[mid] || target < nums[left]) {
left = mid + 1;
}
} else if (nums[mid] < nums[left]) {
if (nums[mid] < target && target <= nums[right]) {
left = mid + 1;
} else if (target < nums[mid] || target > nums[right]) {
right = mid - 1;
}
}
}
// 没有查找到
return false;
}
}
面试题 10.03. 搜索旋转数组⭐⭐⭐⭐
搜索旋转数组。给定一个排序后的数组,包含n个整数,但这个数组已被旋转过很多次了,次数不详。
请编写代码找出数组中的某个元素,假设数组元素原先是按
升序排列的。若有多个相同元素,返回索引值最小的一个。
这道题看起来和81题差不多,81题只是判断数组中存不存在target值,而这一道题是需要返回target的索引,并且如果存在多个元素还要返回索引值最小的一个。
class Solution {
public int search(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
// 将数组尾部与nums[0]相同的元素忽略,使得其二段性恢复。
while (left < right && arr[0] == arr[right]) {
right--;
}
int mid = left + (right - left) / 2;
// 注意:遇到了arr[mid] == target
// 因为我们要找左边界,让 right = mid - 1
if (arr[mid] == target) {
right = mid - 1;
} else if (arr[mid] >= arr[left]) {
if (arr[mid] > target && target >= arr[left]) {
right = mid - 1;
} else if (target > arr[mid] || target < arr[left]) {
left = mid + 1;
}
} else if (arr[mid] < arr[left]) {
if (arr[mid] < target && target <= arr[right]) {
left = mid + 1;
} else if (target < arr[mid] || target > arr[right]) {
right = mid - 1;
}
}
}
// arr = 15, 16, 19, 20, 25, 1, 3, 4, 5, 7, 10, 14 target = 11
// 防止数组中不存在target时, left 越界
if (left == arr.length) {
return -1;
}
return arr[left] == target ? left : -1;
}
}
将题目改成找target有多个相同元素时,找右边界。
class Solution {
public int search(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
// 将数组尾部与nums[0]相同的元素忽略,使得其二段性恢复。
while (left < right && arr[0] == arr[right]) {
right--;
}
int mid = left + (right - left) / 2;
// 注意:遇到了arr[mid] == target
// 因为我们要找左边界,让right = mid - 1
if (arr[mid] == target) {
right = mid - 1;
}
if (arr[mid] >= arr[left]) {
if (arr[mid] > target && target >= arr[left]) {
right = mid - 1;
} else if (target > arr[mid] || target < arr[left]) {
left = mid + 1;
}
} else if (arr[mid] < arr[left]) {
if (arr[mid] < target && target <= arr[right]) {
left = mid + 1;
} else if (target < arr[mid] || target > arr[right]) {
right = mid - 1;
}
}
}
// 防止target比所有数都大此时left最后为arr.length
if (left == arr.length) {
return -1;
}
return arr[left] == target ? left : -1;
}
}
34. 在排序数组中查找元素的第一个和最后一个位置⭐⭐⭐
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
class Solution {
public int[] searchRange(int[] nums, int target) {
// 寻找做边界
int first =leftBound(nums, target);
// 如果说左侧边界找到了,那么一定能找到右侧边界,target只存在一个时,左右索引都是它。
if (first < nums.length && nums[first] == target) {
// 寻找右边界
int second = rightBound(nums, target);
return new int[]{first, second};
} else {
return new int[]{-1, -1};
}
}
/**
* 寻找左侧边界的二分。
*/
private int leftBound(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
right = mid - 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
}
}
return left;
}
/**
* 寻找右侧边界的二分。
*/
private int rightBound(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
left = mid + 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
}
}
return left - 1; // or return right;
}
}
153. 寻找旋转排序数组中的最小值⭐⭐⭐
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
- 若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]
- 若旋转 7 次,则可以得到 [0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
class Solution {
public int findMin(int[] nums) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < nums[right]) {
right = mid;
} else if (nums[mid] >= nums[right]) {
left = mid + 1;
}
}
return nums[left - 1];
}
}
154. 寻找旋转排序数组中的最小值 II⭐⭐⭐
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,4,4,5,6,7] 在变化后可能得到:
- 若旋转 4 次,则可以得到 [4,5,6,7,0,1,4]
- 若旋转 7 次,则可以得到 [0,1,4,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个可能存在 重复 元素值的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须尽可能减少整个过程的操作步骤。
class Solution {
public int findMin(int[] nums) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
// 去除掉两边可能重复的元素
// 时间复杂度:恢复二段性处理中,最坏的情况下(考虑整个数组都是同一个数)复杂度是 O(n)。
// 而之后的找旋转点是「二分」,复杂度为 O(logn)。整体复杂度为 O(n)O(n) 的。
while (left < right && nums[left] == nums[left + 1]) {
left++;
}
while (left < right && nums[right] == nums[right - 1]) {
right--;
}
int mid = left + (right - left) / 2;
if (nums[mid] < nums[right]) {
right = mid;
} else if (nums[mid] >= nums[right]) {
left = mid + 1;
}
}
return nums[left - 1];
}
}
875. 爱吃香蕉的珂珂⭐⭐⭐⭐🍄
珂珂喜欢吃香蕉。这里有 n 堆香蕉,第 i 堆中有 piles[i] 根香蕉。警卫已经离开了,将在 h 小时后回来。
珂珂可以决定她吃香蕉的速度 k (单位:根/小时)。每个小时,她将会选择一堆香蕉,从中吃掉 k 根。
如果这堆香蕉少于 k 根,她将吃掉这堆的所有香蕉,然后这一小时内不会再吃更多的香蕉。
珂珂喜欢慢慢吃,但仍然想在警卫回来前吃掉所有的香蕉。
返回她可以在 h 小时内吃掉所有香蕉的最小速度 k(k 为整数)。
1、确定 x, f(x), target 分别是什么,并写出函数 f 的代码。
自变量 x 是什么呢?回忆之前的函数图像,二分搜索的本质就是在搜索自变量。
所以,题目让求什么,就把什么设为自变量,珂珂吃香蕉的速度就是自变量 x。
那么,在 x 上单调的函数关系 f(x) 是什么?
显然,吃香蕉的速度越快,吃完所有香蕉堆所需的时间就越少,速度和时间就是一个单调函数关系。
所以,f(x) 函数就可以这样定义:
若吃香蕉的速度为 x 根/小时,则需要 f(x) 小时吃完所有香蕉。
代码实现如下:
// 定义:速度为 x 时,需要 f(x) 小时吃完所有香蕉
// f(x) 随着 x 的增加单调递减
int f(int[] piles, int x) {
int hours = 0;
for (int i = 0; i < piles.length; i++) {
hours += piles[i] / x;
if (piles[i] % x > 0) {
hours++;
}
}
return hours;
}
target 就很明显了,吃香蕉的时间限制 H 自然就是 target,是对 f(x) 返回值的最大约束。
2、找到 x 的取值范围作为二分搜索的搜索区间,初始化 left 和 right 变量。
珂珂吃香蕉的速度最小是多少?多大是多少?
显然,最小速度应该是 1,最大速度是 piles 数组中元素的最大值,因为每小时最多吃一堆香蕉,胃口再大也白搭嘛。
这里可以有两种选择,要么你用一个 for 循环去遍历 piles 数组,计算最大值,要么你看题目给的约束,piles 中的元素取值范围是多少,然后给 right 初始化一个取值范围之外的值。
我选择第二种,题目说了 1 <= piles[i] <= 10^9,那么我就可以确定二分搜索的区间边界:
public int minEatingSpeed(int[] piles, int H) {
int left = 1;
// 注意,right 是开区间,所以再加一
int right = 1000000000 + 1;
// ...
}
3、根据题目的要求,确定应该使用搜索左侧还是搜索右侧的二分搜索算法,写出解法代码。
现在我们确定了自变量 x 是吃香蕉的速度,f(x) 是单调递减的函数,target 就是吃香蕉的时间限制 H,题目要我们计算最小速度,也就是 x 要尽可能小:

这就是搜索左侧边界的二分搜索嘛,不过注意 f(x) 是单调递减的,不要闭眼睛套框架,需要结合上图进行思考,写出代码:
public int minEatingSpeed(int[] piles, int H) {
int left = 1;
int right = 1000000000 + 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (f(piles, mid) == H) {
// 搜索左侧边界,则需要收缩右侧边界
right = mid;
} else if (f(piles, mid) < H) {
// 需要让 f(x) 的返回值大一些
right = mid;
} else if (f(piles, mid) > H) {
// 需要让 f(x) 的返回值小一些
left = mid + 1;
}
}
return left;
}
最终代码如下:
class Solution {
public int minEatingSpeed(int[] piles, int h) {
int left = 1;
int right = 1000000000 + 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (f(piles, mid) == h) {
right = mid;
} else if (f(piles, mid) < h) {
right = mid;
} else if (f(piles, mid) > h) {
left = mid + 1;
}
}
return left;
}
int f(int[] piles, int x) {
int hours = 0;
for (int i = 0; i < piles.length; i++) {
hours += piles[i] / x;
if (piles[i] % x > 0) {
hours++;
}
}
return hours;
}
}
1011. 在 D 天内送达包裹的能力🍄
传送带上的包裹必须在 days 天内从一个港口运送到另一个港口。
传送带上的第 i 个包裹的重量为 weights[i]。
每一天,我们都会按给出重量(weights)的顺序往传送带上装载包裹。我们装载的重量不会超过船的最大运载重量。
返回能在 days 天内将传送带上的所有包裹送达的船的最低运载能力。
1、确定 x, f(x), target 分别是什么,并写出函数 f 的代码。
题目问什么,什么就是自变量,也就是说船的运载能力就是自变量 x。
运输天数和运载能力成反比,所以可以让 f(x) 计算 x 的运载能力下需要的运输天数,那么 f(x) 是单调递减的。
函数 f(x) 的实现如下:
// 定义:当运载能力为 x 时,需要 f(x) 天运完所有货物
// f(x) 随着 x 的增加单调递减
int f(int[] weights, int x) {
int days = 0;
for (int i = 0; i < weights.length; ) {
// 尽可能多装货物
int cap = x;
while (i < weights.length) {
if (cap < weights[i]) {
break;
} else {
cap -= weights[i];
}
i++;
}
days++;
}
return days;
}
对于这道题,target 显然就是运输天数 D,我们要在 f(x) == D 的约束下,算出船的最小载重。
2、找到 x 的取值范围作为二分搜索的搜索区间,初始化 left 和 right 变量。
船的最小载重是多少?最大载重是多少?
显然,船的最小载重应该是 weights 数组中元素的最大值,因为每次至少得装一件货物走,不能说装不下嘛。
最大载重显然就是weights 数组所有元素之和,也就是一次把所有货物都装走。
这样就确定了搜索区间 [left, right):
public int shipWithinDays(int[] weights, int days) {
int left = 0;
// 注意,right 是开区间,所以额外加一
int right = 1;
for (int w : weights) {
left = Math.max(left, w);
right += w;
}
// ...
}
3、需要根据题目的要求,确定应该使用搜索左侧还是搜索右侧的二分搜索算法,写出解法代码。
现在我们确定了自变量 x 是船的载重能力,f(x) 是单调递减的函数,target 就是运输总天数限制 D,题目要我们计算船的最小载重,也就是 x 要尽可能小:
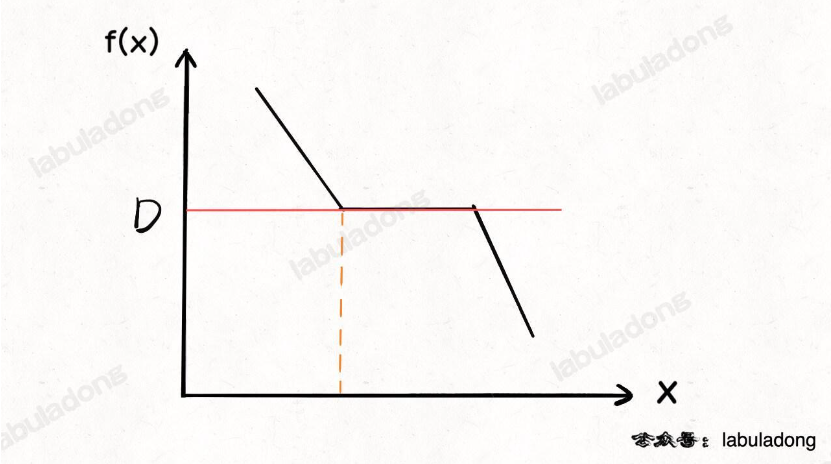
这就是搜索左侧边界的二分搜索嘛,结合上图就可写出二分搜索代码:
class Solution {
public int shipWithinDays(int[] weights, int days) {
int left = 0, right = 1;
for (int w : weights) {
left = Math.max(left, w);
right += w;
}
// 单调递减的
while (left < right) {
int mid = (left + right) / 2;
if (f(weights, mid) == days) {
right = mid;
} else if (f(weights, mid) < days) {
right = mid;
} else if (f(weights, mid) > days) {
left = mid + 1;
}
}
return left;
}
// 我怎么感觉这段代码也非常之优雅!!!!
private int f(int[] weights, int x) {
int days = 0;
for (int i = 0; i < weights.length;) {
int cap = x;
while (i < weights.length) {
if (cap < weights[i]) {
break;
} else {
cap -= weights[i];
}
i++;
}
days++;
}
return days;
}
}
410. 分割数组的最大值(记忆化递归)🍄
给定一个非负整数数组 nums 和一个整数 m ,你需要将这个数组分成 m 个非空的连续子数组。
设计一个算法使得这 m 个子数组各自和的最大值最小。
输入:nums = [7,2,5,10,8], m = 2
输出:18
解释:
一共有四种方法将 nums 分割为 2 个子数组。
其中最好的方式是将其分为 [7,2,5] 和 [10,8] 。
因为此时这两个子数组各自的和的最大值为18,在所有情况中最小。
这道题居然和1011题一模一样,只是换了一种说法,感觉真神奇啊!!!
你只有一艘货船,现在有若干货物,每个货物的重量是 nums[i],现在你需要在 m 天内将这些货物运走。
请问你的货船的最小载重是多少?
这不就是刚才我们解决的力扣第 1011 题「在 D 天内送达包裹的能力」吗?
货船每天运走的货物就是 nums 的一个子数组;在 m 天内运完就是将 nums 划分成 m 个子数组;
让货船的载重尽可能小,就是让所有子数组中最大的那个子数组元素之和尽可能小。
所以这道题的解法直接复制粘贴运输问题的解法代码即可:
class Solution {
public int splitArray(int[] nums, int m) {
return shipWithinDays(nums, m);
}
public int shipWithinDays(int[] weights, int days) {
int left = 0, right = 1;
for (int i = 0; i < weights.length; i++) {
left = Math.max(left, weights[i]);
right += weights[i];
}
while (left < right) {
int mid = (left + right) / 2;
if (f(weights, mid) == days) {
right = mid;
} else if (f(weights, mid) < days) {
right = mid;
} else if (f(weights, mid) > days) {
left = mid + 1;
}
}
return left;
}
private int f(int[] weights, int x) {
int days = 0;
for (int i = 0; i < weights.length;) {
int cap = x;
while (i < weights.length) {
if (cap < weights[i]) {
break;
} else {
cap -= weights[i];
}
i++;
}
days++;
}
return days;
}
}
滑动窗口
3. 无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
class Solution {
public int lengthOfLongestSubstring(String s) {
// 定义返回的最大长度,左右指针。
int Max = 0, left = 0, right = 0;
char[] charArray = s.toCharArray();
// 用Set来去重
Set<Character> set = new HashSet<>();
for (int i = 0; i < s.length(); i++) {
// 如果当前字母加入窗口中会造成重复,则不断移动左指针直到没有重复字母为止。
while (set.contains(charArray[i])) {
set.remove(charArray[left++]);
}
// 当不会造成重复时加入
set.add(charArray[i]);
// right 指针右移
right++;
int tempLen = right - left;
// 尝试更新最大值
Max = Math.max(tempLen, Max);
}
return Max;
}
}
class Solution {
public int lengthOfLongestSubstring(String s) {
HashMap<Character, Integer> window = new HashMap<>();
int left = 0, right = 0;
int res = 0;
while (right < s.length()) {
char c = s.charAt(right);
right++;
window.put(c, window.getOrDefault(c, 0) + 1);
while (window.get(c) > 1) {
char d = s.charAt(left);
left++;
window.put(d, window.get(d) - 1);
}
res = Math.max(res, right - left);
}
return res;
}
}
剑指 Offer 57 - II. 和为s的连续正数序列
输入一个正整数 target ,输出所有和为 target 的连续正整数序列(至少含有两个数)。
序列内的数字由小到大排列,不同序列按照首个数字从小到大排列。
class Solution {
public int[][] findContinuousSequence(int target) {
int end = target / 2;
int left = 1, right = 1;
int sum = 0;
ArrayList<int[]> res = new ArrayList<>();
// 窗口的左边是窗口内的最小数字,只能小于等于target / 2
// 因为需要至少两个数的和为target,当超过了target的一半时,此时任意两个连续数的和一定是大于target的。
// 有一个数大于target的一半时可能满足条件 比如当target==7时,3,4就是这种情况
while (left <= end) {
sum += right;
right++;
// 移动窗口左侧,这里要用while
// 如果右边刚加入了一个较大的数
// 也许左侧需要移动几个位置,才能使和 <= target
while (sum > target) {
sum = sum - left;
left++;
}
if (sum == target) {
int[] temp = new int[right - left];
for (int i = 0; i < temp.length; i++) {
temp[i] = left + i;
}
res.add(temp);
}
}
return res.toArray(new int[res.size()][]);
}
}
76. 最小覆盖子串⭐
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
注意:
- 对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量;
- 如果 s 中存在这样的子串,我们保证它是唯一的答案。
class Solution {
public String minWindow(String s, String t) {
HashMap<Character, Integer> needs = new HashMap<>();
HashMap<Character, Integer> window = new HashMap<>();
for (Character ch : t.toCharArray()) {
needs.put(ch, needs.getOrDefault(ch, 0) + 1);
}
int left = 0, right = 0;
int valid = 0;
int start = 0, len = Integer.MAX_VALUE;
while (right < s.length()) {
// 即将移入窗口的字符
char c = s.charAt(right);
// 增大窗口
right++;
// 进行窗口内数据的一系列更新
if (needs.containsKey(c)) {
window.put(c, window.getOrDefault(c, 0) + 1);
// Integer会缓存频繁使用的数值,
// 数值范围为-128到127,在此范围内直接返回缓存值,超过范围就会new对象。
// 比如两个Integer对象数值为128,当用==比较时是比较两个对象的引用,会得出不等。
// 用equals判断两个Integer的数值是否相等
if (window.get(c).equals(needs.get(c))) {
valid++;
}
}
// 判断左侧窗口是否要收缩,当窗口已经包含t中所有的字符,就要缩小窗口了
// 因为题目是要求包含t所有字符的最短字符串,已经找到一个满足条件的字符串窗口继续增大,字符会增加,没必要。
// 我们缩短左侧窗口看是否能够找到更短的能满足条件的字符串。
while (valid == needs.size()) {
// 当窗口内的字符包含t中所有的字符时,如果长度更小,记录下窗口的起点及长度。
if (right - left < len) {
start = left;
len = right - left;
}
// d 是将移出窗口的字符
char d = s.charAt(left);
left++;
// 进行窗口内数据的一系列更新
if (needs.containsKey(d)) {
if (window.get(d).equals(needs.get(d))) {
valid--;
}
window.put(d, window.get(d) - 1);
}
}
}
return len == Integer.MAX_VALUE ? "" : s.substring(start, start + len);
}
}
187. 重复的DNA序列
DNA序列 由一系列核苷酸组成,缩写为 'A', 'C', 'G' 和 'T'.。
- 例如,"ACGAATTCCG" 是一个 DNA序列 。
在研究 DNA 时,识别 DNA 中的重复序列非常有用。
给定一个表示 DNA序列 的字符串 s ,返回所有在 DNA 分子中出现不止一次的 长度为 10 的序列(子字符串)。
你可以按任意顺序返回答案。
字符串哈希:
class Solution {
List<String> findRepeatedDnaSequences(String s) {
// 先把字符串转化成四进制的数字数组
int[] nums = new int[s.length()];
for (int i = 0; i < nums.length; i++) {
switch (s.charAt(i)) {
case 'A':
nums[i] = 0;
break;
case 'G':
nums[i] = 1;
break;
case 'C':
nums[i] = 2;
break;
case 'T':
nums[i] = 3;
break;
}
}
// 记录重复出现的哈希值
HashSet<Integer> seen = new HashSet<>();
// 记录重复出现的字符串结果
HashSet<String> res = new HashSet<>();
// 数字位数
int L = 10;
// 进制
int R = 4;
// 存储 R^(L - 1) 的结果
int RL = (int) Math.pow(R, L - 1);
// 维护滑动窗口中字符串的哈希值
int windowHash = 0;
// 滑动窗口代码框架,时间 O(N)
int left = 0, right = 0;
while (right < nums.length) {
// 扩大窗口,移入字符,并维护窗口哈希值(在最低位添加数字)
windowHash = R * windowHash + nums[right];
right++;
// 当子串的长度达到要求
if (right - left == L) {
// 根据哈希值判断是否曾经出现过相同的子串
if (seen.contains(windowHash)) {
// 当前窗口中的子串是重复出现的
res.add(s.substring(left, right));
} else {
// 当前窗口中的子串之前没有出现过,记下来
seen.add(windowHash);
}
// 缩小窗口,移出字符,并维护窗口哈希值(删除最高位数字)
windowHash = windowHash - nums[left] * RL;
left++;
}
}
// 转化成题目要求的 List 类型
return new LinkedList<>(res);
}
}
简单写法:
class Solution {
public List<String> findRepeatedDnaSequences(String s) {
int left = 0, right = 9;
HashMap<String, Integer> map = new HashMap<>();
List<String> res = new ArrayList<>();
String t;
while (right < s.length()) {
t = s.substring(left, right + 1);
map.put(t, map.getOrDefault(t, 0) + 1);
if (map.get(t) == 2) {
res.add(t);
}
left++;
right++;
}
return res;
}
}
class Solution {
public List<String> findRepeatedDnaSequences(String s) {
int n = s.length();
int[] nums = new int[n];
for (int i = 0; i < n; i++) {
if (s.charAt(i) == 'A') {
nums[i] = 0;
} else if (s.charAt(i) == 'C') {
nums[i] = 1;
} else if (s.charAt(i) == 'G') {
nums[i] = 2;
} else if (s.charAt(i) == 'T') {
nums[i] = 3;
}
}
List<String> res = new ArrayList<>();
HashMap<Integer, Integer> seen = new HashMap<>();
int window = 0;
int left = 0;
int right = 0;
while (right < n) {
window = window * 4 + nums[right];
right++;
if (right - left == 10) {
seen.put(window, seen.getOrDefault(window, 0) + 1);
if (seen.get(window) == 2) {
res.add(s.substring(left, right));
}
window = (int) (window - nums[left] * Math.pow(4, 9));
left++;
}
}
return res;
}
}
209. 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。
如果不存在符合条件的子数组,返回 0 。
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int left = 0;
int right = 0;
int sum = 0;
int len = Integer.MAX_VALUE;
while (right < nums.length) {
int c = nums[right];
right++;
sum = sum + c;
// 一直将左窗口移动使sum < target为止。这时再进入下一轮循环移动右窗口。
while (sum >= target) {
len = Math.min(len, right - left);
sum =sum - nums[left];
left++;
}
}
return len == Integer.MAX_VALUE ? 0 : len;
}
}
713 & 剑指 Offer II 009. 乘积小于 K 的子数组⭐
给定一个正整数数组 nums和整数 k ,请找出该数组内乘积小于 k 的连续的子数组的个数。
输入: nums = [10,5,2,6], k = 100
输出: 8
解释: 8 个乘积小于 100 的子数组分别为: [10], [5], [2], [6], [10,5], [5,2], [2,6], [5,2,6]。
需要注意的是 [10,5,2] 并不是乘积小于100的子数组。
class Solution {
public int numSubarrayProductLessThanK(int[] nums, int k) {
int left = 0, right = 0;
int windowProduct = 1;
int count = 0;
while (right < nums.length) {
// 扩大窗口
int c = nums[right];
windowProduct = windowProduct * c;
right++;
// 窗口可能需要移动不止1个位置才使乘积小于k
// 右边如果乘了一个很大的数,左边可能需要移动几个位置
// 所以这里用while循环,类似于第三题的while循环。
// left < right 是因为遇到有些情况windowProduct >= k会一直满足,一直移动left指针,导致nums[left]出现下标越界。
while (left < right && windowProduct >= k) {
// 缩小窗口
windowProduct = windowProduct / nums[left];
left++;
}
// 现在必然是一个合法的窗口,但注意思考这个窗口中的子数组个数怎么计算:
// 比方说 left = 1, right = 4 划定了 [1, 2, 3] 这个窗口(right 是开区间)
// 其中所有可能的子数组为 [1], [2], [3], [1,2], [2,3], [1,2,3]
// 而我们只需要记录 [3], [2,3], [1,2,3] 这 right - left 个子数组即可
// 因为 [1], [2], [1,2] 已经在滑动窗口为 [1, 2] 时计算过了
count = count + right - left;
}
return count;
}
}
219. 存在重复元素 II⭐
给你一个整数数组 nums 和一个整数 k ,判断数组中是否存在两个 不同的索引 i 和 j ,满足 nums[i] == nums[j] 且 abs(i - j) <= k 。如果存在,返回 true ;否则,返回 false 。
class Solution {
public boolean containsNearbyDuplicate(int[] nums, int k) {
HashMap<Integer, Integer> window = new HashMap<>();
int right = 0;
while (right < nums.length) {
int c = nums[right];
if (window.containsKey(c)) {
if (right - window.get(c) <= k) {
return true;
}
}
window.put(c, right);
right++;
}
return false;
}
}
220. 存在重复元素 III⭐
给你一个整数数组 nums 和两个整数 k 和 t 。请你判断是否存在 两个不同下标 i 和 j,使得 abs(nums[i] - nums[j]) <= t ,同时又满足 abs(i - j) <= k 。如果存在则返回 true,不存在返回 false。
class Solution {
public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
TreeSet<Integer> window = new TreeSet<>();
int left = 0, right = 0;
while (right < nums.length) {
// 为了防止 i == j,所以在扩大窗口之前先判断是否有符合题意的索引对 (i, j)
// 查找略大于 nums[right] 的那个元素
Integer ceiling = window.ceiling(nums[right]);
if (ceiling != null && (long) ceiling - nums[right] <= t) {
return true;
}
// 查找略小于 nums[right] 的那个元素
Integer floor = window.floor(nums[right]);
if (floor != null && (long) nums[right] - floor <= t) {
return true;
}
// 扩大窗口
window.add(nums[right]);
right++;
// 当窗口大小大于k时,缩小窗口。
if (right - left > k) {
// 缩小窗口
window.remove(nums[left]);
left++;
}
}
return false;
}
}
239. 滑动窗口最大值⭐⭐⭐
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。
滑动窗口每次只向右移动一位。返回滑动窗口中的最大值 。
// 构建一个单调队列保证队列中的元素是递减的 从first往last方向看是递减的
class MyQueue {
Deque<Integer> deque = new LinkedList<>();
// 删除元素时判断要删除的元素是不是当前单调队列中最大的元素
// 同时判断队列当前是否为空
void poll(int val) {
if (val == deque.peek()) {
deque.poll();
}
}
// 一个LinkedList 是这样的 first ------ last
// 添加元素时,如果要添加的元素大于入口处的元素,就将入口元素弹出。
// 保证队列元素单调递减。
// 比如此时队列元素3,1,2将要入队,比1大,所以1弹出,此时队列:3,2
void add(int val) {
// 注意这个while循环,在一个值val添加到队列时,会与队列尾部元素进行比较
// 将队列中所有比添加的值val小的值移除之后,再将val入队。
while (!deque.isEmpty() && val > deque.getLast()) {
deque.removeLast();
}
// 是从last那边添加,感觉就相当于addLast。
deque.addLast(val);
}
// 队列队头元素始终为最大值,这就要求我们在添加元素时,把值小于要添加的元素的值都删掉。
int peek() {
return deque.peek();
}
}
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if (nums.length == 1) {
return nums;
}
// 就相当于数组长度nums.length可以允许存在多少个长度为k的窗口
int len = nums.length - k + 1;
// 存放结果元素的数组
int[] res = new int[len];
int num = 0;
// 自定义队列
MyQueue myQueue = new MyQueue();
// 先将前k的元素放入队列
for (int i = 0; i < k; i++) {
myQueue.add(nums[i]);
}
// 把第一个窗口中最大的元素加入结果集
res[num++] = myQueue.peek();
for (int i = 0; i < nums.length - k; i++) {
// 注意要先移除再添加
// 滑动窗口移除最前面的元素,移除是判断该元素是否放入队列
myQueue.poll(nums[i]);
// 滑动窗口加入最后面的元素
myQueue.add(nums[i + k]);
// 记录对应的最大值
res[num++] = myQueue.peek();
}
return res;
}
}
class MyQueue {
Deque<Integer> deque = new LinkedList<>();
void poll(int val) {
// 判断要删除的元素是否是最大值,是最大值就删除
if (val == peek()) {
deque.removeFirst();
}
}
void add(int val) {
// 这里要判断队列是否为空,如果要添加的元素,比队列中的元素都大,则会将他们全部移除,导致队列为空。
// 当队列为空时再调用getLast会抛出NoSuchElementException。
while (!deque.isEmpty() && val > deque.getLast()) {
deque.removeLast();
}
deque.addLast(val);
}
int peek() {
return deque.peek();
}
}
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
MyQueue window = new MyQueue();
List<Integer> res = new ArrayList<>();
for (int i = 0; i < nums.length; i++) {
if (i < k - 1) {
//先填满窗口的前 k - 1
window.add(nums[i]);
} else {
// 窗口向前滑动,加入新数字
window.add(nums[i]);
// 记录当前窗口的最大值
res.add(window.peek());
// 移出旧数字
window.poll(nums[i - k + 1]);
}
}
// 需要转成 int[] 数组再返回
int[] arr = new int[res.size()];
for (int i = 0; i < res.size(); i++) {
arr[i] = res.get(i);
}
return arr;
}
}
395. 至少有 K 个重复字符的最长子串⭐⭐
这道题难度还是挺大的,不过用 滑动窗口算法框架 讲的代码框架,稍微修改下就能做这道题。
前文 滑动窗口框架 说过,使用滑动窗口算法需要搞清楚以下几个问题:
1、什么时候应该扩大窗口?
2、什么时候应该缩小窗口?
3、什么时候得到一个合法的答案?
在本题的场景中,我们想尽可能多地装字符,即扩大窗口,但不知道什么时候应该开始收缩窗口。
为什么呢?比如窗口中有些字符出现次数不满足 k,但有可能再扩大扩大窗口就能满足 k 了呀?但要这么说的话,你干脆一直扩大窗口算了,所以你说不准啥时候应该收缩窗口。
理论上讲,这种情况就不能用滑动窗口模板了,但有时候我们可以自己添加一些约束,来进行窗口的收缩。
题目说让我们求每个字符都出现至少 k 次的子串,我们可以再添加一个约束条件:求每个字符都出现至少 k 次,仅包含 count 种不同字符的最长子串。
即实现一个函数签名如下的算法:
// 在 s 中寻找仅含有 count 种字符,且每种字符出现次数都大于 k 的最长子串
int logestKLetterSubstr(String s, int k, int count) {
添加了字符种类的限制,我们就可以回答滑动窗口算法的三个灵魂问题了:
1、什么时候应该扩大窗口?窗口中字符种类小于 count 时扩大窗口。
2、什么时候应该缩小窗口?窗口中字符种类大于 count 时扩大窗口。
3、什么时候得到一个合法的答案?窗口中所有字符出现的次数都大于等于 k 时,得到一个合法的子串。
然后就可以套用滑动窗口算法模板实现 logestKLetterSubstr 函数了。
当然,题目没有 count 的约束,那没关系呀,count 能有几种取值?因为 s 中只包含小写字母,所以 count 的取值也就是 1~26,所以最后用一个 for 循环把
这些值都输入 logestKLetterSubstr 计算一遍,求最大值就是题目想要的答案了。这充分体现了前文 我的刷题经验总结 中所说:算法的本质是穷举。
滑动窗口算法的时间复杂度是 O(N),循环 26 次依然是 O(26N) = O(N)。
class Solution {
public int longestSubstring(String s, int k) {
int len = 0;
for (int i = 1; i <= 26; i++) {
// 限制窗口中只能有 i 种不同字符
len = Math.max(len, logestKLetterSubstr(s, k, i));
}
return len;
}
// 寻找 s 中含有 count 种字符,且每种字符出现次数都大于 k 的子串
int logestKLetterSubstr(String s, int k, int count) {
// 记录答案
int res = 0;
// 快慢指针维护滑动窗口,左闭右开区间
int left = 0, right = 0;
// 题目说 s 中只有小写字母,所以用大小 26 的数组记录窗口中字符出现的次数
int[] windowCount = new int[26];
// 记录窗口中存在几种不同的字符(字符种类)
int windowUniqueCount = 0;
// 记录窗口中有几种字符的出现次数达标(大于等于 k)
int windowValidCount = 0;
// 滑动窗口代码模板
while (right < s.length()) {
// 移入字符,扩大窗口
char c = s.charAt(right);
if (windowCount[c - 'a'] == 0) {
// 窗口中新增了一种字符
windowUniqueCount++;
}
windowCount[c - 'a']++;
if (windowCount[c - 'a'] == k) {
// 窗口中新增了一种达标的字符
windowValidCount++;
}
right++;
// 当窗口中字符种类大于 k 时,缩小窗口
// 当窗口内的字符种类大于了限制类型数时,就要缩小窗口了。
// 这里要用while因为有可能左边有多个相同的字符,移动一次并不能使字符种类减少。
// 一直移动到字符种类等于限制count为止。
while (windowUniqueCount > count) {
// 移出字符,缩小窗口
char d = s.charAt(left);
if (windowCount[d - 'a'] == k) {
// 窗口中减少了一种达标的字符
windowValidCount--;
}
windowCount[d - 'a']--;
if (windowCount[d - 'a'] == 0) {
// 窗口中减少了一种字符
windowUniqueCount--;
}
left++;
}
// 当窗口中字符种类为 count 且每个字符出现次数都满足 k 时,更新答案
if (windowValidCount == count) {
res = Math.max(res, right - left);
}
}
return res;
}
}
424. 替换后的最长重复字符⭐
给你一个字符串 s 和一个整数 k 。你可以选择字符串中的任一字符,并将其更改为任何其他大写英文字符。
该操作最多可执行 k 次。在执行上述操作后,返回包含相同字母的最长子字符串的长度。
class Solution {
public int characterReplacement(String s, int k) {
int left = 0, right = 0;
int[] windowCharCount = new int[26];
// 窗口内重复字符出现最多的次数
int windowMaxCount = 0;
int res = 0;
while (right < s.length()) {
windowCharCount[s.charAt(right) - 'A']++;
windowMaxCount = Math.max(windowMaxCount, windowCharCount[s.charAt(right) - 'A']);
right++;
if (right - left - windowMaxCount > k) {
windowCharCount[s.charAt(left) - 'A']--;
left++;
// 疑惑为什么移动了窗口不用更新windowMaxCount。
// 因为每轮循环的窗口大小都是比最长序列长度大一,是要你去测试这个窗口长度是否可行。
// 如果左边缩小窗口时,将出现次数最多的字符移除了一个,那么不管下一轮新加入窗口的字符是不是出现最多的字符。
// 都不能保证right - left - windowMaxCount > k
// 1、新加入窗口的字符是出现最多的字符,删了一个字符又加入一个新的重复字符,其余不是重复最多的字符没变,和上一轮情况一样。
// 2、新加入窗口的字符不是出现最多的字符,删了一个出现最多的字符,结果还加了一个不是出现最多的字符,需要替换的字符就更多了。
// 比上一轮还多,上一轮都不满足最多替换k个字符,这一轮依然不满足。
// 可以看出这种情况windowMaxCount要么是不变,要么还减小了。
}
// 满足最多执行k次窗口中的字符全是相同的
// 更新结果为窗口的大小
res = Math.max(res, right - left);
}
return res;
}
}
1004. 最大连续1的个数 III⭐
给定一个二进制数组 nums 和一个整数 k,如果可以翻转最多 k 个 0 ,则返回 数组中连续 1 的最大个数 。
class Solution {
public int longestOnes(int[] nums, int k) {
int left = 0, right = 0;
// 记录窗口中 1 的出现次数
int windowOneCount = 0;
// 记录结果长度
int res = 0;
// 开始滑动窗口模板
while (right < nums.length) {
// 扩大窗口
if (nums[right] == 1) {
windowOneCount++;
}
right++;
while (right - left - windowOneCount > k) {
// 当窗口中需要替换的 0 的数量大于 k,缩小窗口
if (nums[left] == 1) {
windowOneCount--;
}
left++;
}
// 此时一定是一个合法的窗口,求最大窗口长度
res = Math.max(res, right - left);
}
return res;
}
}
438. 找到字符串中所有字母异位词⭐
给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
class Solution {
public List<Integer> findAnagrams(String s, String p) {
HashMap<Character, Integer> need = new HashMap<>();
HashMap<Character, Integer> window = new HashMap<>();
List<Integer> res = new ArrayList<>();
for (Character ch : p.toCharArray()) {
need.put(ch, need.getOrDefault(ch, 0) + 1);
}
int left = 0, right = 0;
int start = 0, len = Integer.MAX_VALUE;
int valid = 0;
while (right < s.length()) {
char c = s.charAt(right);
right++;
if (need.containsKey(c)) {
window.put(c, window.getOrDefault(c, 0) + 1);
if (window.get(c).equals(need.get(c))) {
valid++;
}
}
if (right - left == p.length()) {
start = left;
if (valid == need.size()) {
res.add(start);
}
char d = s.charAt(left);
left++;
if (need.containsKey(d)) {
if (window.get(d).equals(need.get(d))) {
valid--;
}
window.put(d, window.get(d) - 1);
}
}
}
return res;
}
}
567. 字符串的排列⭐
给你两个字符串 s1 和 s2 ,写一个函数来判断 s2 是否包含 s1 的排列。如果是,返回 true ;否则,返回 false 。
换句话说,s1 的排列之一是 s2 的 子串 。
输入:s1 = "ab" s2 = "eidbaooo"
输出:true
解释:s2 包含 s1 的排列之一 ("ba")
class Solution {
public boolean checkInclusion(String s1, String s2) {
int m = s1.length(), n = s2.length();
// 当s1的长度大于s2的长度时直接返回false。
if (m > n) {
return false;
}
// 仅包含小写字母
int[] cs1 = new int[26];
int[] cs2 = new int[26];
// 以s1字符串的长度为固定滑动窗口的大小
// 首先确定一个初始窗口
for (int i = 0; i < m; i++) {
cs1[s1.charAt(i) - 'a']++;
cs2[s2.charAt(i) - 'a']++;
}
// 比较两个数组中对应索引位置的元素是不是相等
if (Arrays.equals(cs1, cs2)) {
return true;
}
// 移动滑动窗口
for (int i = m; i < n; i++) {
// 删除一个元素
cs2[s2.charAt(i - m) - 'a']--;
// 添加一个元素
cs2[s2.charAt(i) - 'a']++;
if (Arrays.equals(cs1, cs2)) {
return true;
}
}
return false;
}
}
滑动窗口模板
class Solution {
public boolean checkInclusion(String s1, String s2) {
HashMap<Character, Integer> need = new HashMap<>();
HashMap<Character, Integer> window = new HashMap<>();
for (char ch : s1.toCharArray()) {
need.put(ch, need.getOrDefault(ch, 0) + 1);
}
int left = 0, right = 0;
int valid = 0;
// 在s2字符串上滑动窗口
while (right < s2.length()) {
char c = s2.charAt(right);
right++;
if (need.containsKey(c)) {
window.put(c, window.getOrDefault(c, 0) + 1);
if (window.get(c).equals(need.get(c))) {
valid++;
}
}
// 窗口是左闭右开的,当窗口大小等于s1字符串的长度时
// 首先判断是否找到了满足条件的子串
// 没找到就移动窗口
while (right - left == s1.length()) {
if (valid == need.size()) {
return true;
}
// 要移除窗口的字符
char d = s2.charAt(left);
left++;
if (need.containsKey(d)) {
if (window.get(d).equals(need.get(d))) {
valid--;
}
window.put(d, window.get(d) - 1);
}
}
}
return false;
}
}
594. 最长和谐子序列
和谐数组是指一个数组里元素的最大值和最小值之间的差别 正好是 1 。
现在,给你一个整数数组 nums ,请你在所有可能的子序列中找到最长的和谐子序列的长度。
数组的子序列是一个由数组派生出来的序列,它可以通过删除一些元素或不删除元素、且不改变其余元素的顺序而得到。
class Solution {
public int findLHS(int[] nums) {
Arrays.sort(nums);
int left = 0, right = 0, max = Integer.MIN_VALUE;
while (right < nums.length) {
int c = nums[right];
right++;
if (c - nums[left] > 1) {
left++;
}
if (c - nums[left] == 1) {
max = Math.max(max, right - left);
}
}
return max == Integer.MIN_VALUE ? 0 : max;
}
}
862. 和至少为 K 的最短子数组(单调队列)⭐⭐⭐
给你一个整数数组 nums 和一个整数 k ,找出 nums 中和至少为 k 的最短非空子数组 ,并返回该子数组的长度。如果不存在这样的 子数组 ,返回 -1 。
子数组是数组中连续的一部分。
class Solution {
public int shortestSubarray(int[] nums, int k) {
int n = nums.length;
// 看题目的数据范围,前缀和数组中元素可能非常大,所以用 long类型。
long[] preSum = new long[n + 1];
// 计算 nums 的前缀和数组
for (int i = 0; i < n; i++) {
preSum[i + 1] = preSum[i] + nums[i];
}
// 单调队列辅助滑动窗口算法
MyQueue window = new MyQueue();
int right = 0, left = 0;
int len = Integer.MAX_VALUE;
// 开始执行滑动窗口算法框架
while (right < preSum.length) {
// 扩大窗口,元素入队
window.add(preSum[right]);
right++;
// 若新进入窗口的元素和窗口中的最小值之差大于等于 k,
// 说明得到了符合条件的子数组,缩小窗口,使子数组长度尽可能小
// 前面两个判断是防止preSum[right]下标越界
// 当window为空时,window.peek()为null,要做减法会调用longValue转为long类型,可是此时为null。
// 抛出空指针异常,这些细节一定要注意。
while (right < preSum.length && !window.isEmpty() && preSum[right] - window.peek() >= k) {
// 更新答案
len = Math.min(len, right - left);
// 缩小窗口
window.poll(preSum[left]);
left++;
}
}
return len == Integer.MAX_VALUE ? -1 : len;
}
}
/**
* 单调增的队列,队头就是最小的元素。
*/
class MyQueue {
Deque<Long> deque = new LinkedList<>();
void poll(long val) {
// 判断要删除的元素是否是最小值,是最小值就删除
if (val == peek()) {
deque.removeFirst();
}
}
void add(long val) {
// 这里要判断队列是否为空,如果要添加的元素,比队列中的元素都小,则会将他们全部移除,导致队列为空。
// 当队列为空时再调用getLast会抛出NoSuchElementException。
while (!deque.isEmpty() && val < deque.getLast()) {
deque.removeLast();
}
deque.addLast(val);
}
long peek() {
return deque.peek();
}
boolean isEmpty() {
return deque.isEmpty();
}
}
918. 环形子数组的最大和(单调队列)⭐⭐⭐
给定一个长度为 n 的环形整数数组 nums ,返回 nums 的非空 子数组 的最大可能和 。
环形数组 意味着数组的末端将会与开头相连呈环状。
形式上, nums[i] 的下一个元素是 nums[(i + 1) % n] , nums[i] 的前一个元素是 nums[(i - 1 + n) % n] 。
子数组 最多只能包含固定缓冲区 nums 中的每个元素一次。
形式上,对于子数组 nums[i], nums[i + 1], ..., nums[j] ,不存在 i <= k1, k2 <= j 其中 k1 % n == k2 % n 。
class Solution {
public int maxSubarraySumCircular(int[] nums) {
int n = nums.length;
// 模拟环状的 nums 数组
int[] preSum = new int[2 * n + 1];
preSum[0] = 0;
// 计算环状 nums 的前缀和
for (int i = 1; i < preSum.length; i++) {
preSum[i] = preSum[i - 1] + nums[(i - 1) % n];
}
// 记录答案
// 维护一个滑动窗口,以便根据窗口中的最小值计算最大子数组和。
int maxSum = Integer.MIN_VALUE;
MonotonicQueue<Integer> window = new MonotonicQueue<>();
window.push(0);
for (int i = 1; i < preSum.length; i++) {
maxSum = Math.max(maxSum, preSum[i] - window.min());
// 维护窗口的大小为 nums 数组的大小
if (window.size() == n) {
window.pop();
}
window.push(preSum[i]);
}
return maxSum;
}
}
/* 单调队列的实现,可以高效维护最大值和最小值 */
class MonotonicQueue<E extends Comparable<E>> {
// 常规队列,存储所有元素
LinkedList<E> q = new LinkedList<>();
// 元素降序排列的单调队列,头部是最大值
LinkedList<E> maxq = new LinkedList<>();
// 元素升序排列的单调队列,头部是最小值
LinkedList<E> minq = new LinkedList<>();
public void push(E elem) {
// 维护常规队列,直接在队尾插入元素
q.addLast(elem);
// 维护 maxq,将小于 elem 的元素全部删除
while (!maxq.isEmpty() && maxq.getLast().compareTo(elem) < 0) {
maxq.pollLast();
}
maxq.addLast(elem);
// 维护 minq,将大于 elem 的元素全部删除
while (!minq.isEmpty() && minq.getLast().compareTo(elem) > 0) {
minq.pollLast();
}
minq.addLast(elem);
}
public E max() {
// maxq 的头部是最大元素
return maxq.getFirst();
}
public E min() {
// minq 的头部是最大元素
return minq.getFirst();
}
public E pop() {
// 从标准队列头部弹出需要删除的元素
E deleteVal = q.pollFirst();
assert deleteVal != null;
// 由于 push 的时候会删除元素,deleteVal 可能已经被删掉了
if (deleteVal.equals(maxq.getFirst())) {
maxq.pollFirst();
}
if (deleteVal.equals(minq.getFirst())) {
minq.pollFirst();
}
return deleteVal;
}
public int size() {
// 标准队列的大小即是当前队列的大小
return q.size();
}
public boolean isEmpty() {
return q.isEmpty();
}
}
643. 子数组最大平均数 I(固定窗口)
给你一个由 n 个元素组成的整数数组 nums 和一个整数 k 。
请你找出平均数最大且 长度为 k 的连续子数组,并输出该最大平均数。
任何误差小于 10-5 的答案都将被视为正确答案。
输入:nums = [1,12,-5,-6,50,3], k = 4
输出:12.75
解释:最大平均数 (12-5-6+50)/4 = 51/4 = 12.75
提示:
- n == nums.length
- 1 <= k <= n <= 105
- -10^4 <= nums[i] <= 10^4
因为这个题目说的是找平均数最大的长度为k的子数组,不是说找平均数最大的子数组。
先初始化一个k的窗口,求出平均数。然后一直往后移动。
class Solution {
public double findMaxAverage(int[] nums, int k) {
double max = 0;
double sum = 0;
for (int i = 0; i < k; i++) {
sum += nums[i];
}
max = sum / k;
for (int i = k; i < nums.length; i++) {
sum = sum - nums[i - k] + nums[i];
max = Math.max(max, sum / k);
}
return max;
}
}
1423. 可获得的最大点数(固定窗口)⭐
几张卡牌 排成一行,每张卡牌都有一个对应的点数。点数由整数数组 cardPoints 给出。
每次行动,你可以从行的开头或者末尾拿一张卡牌,最终你必须正好拿 k 张卡牌。
你的点数就是你拿到手中的所有卡牌的点数之和。
给你一个整数数组 cardPoints 和整数 k,请你返回可以获得的最大点数。
输入:cardPoints = [1,2,3,4,5,6,1], k = 3
输出:12
解释:第一次行动,不管拿哪张牌,你的点数总是 1 。但是,先拿最右边的卡牌将会最大化你的可获得点数。最优策略是拿右边的三张牌,最终点数为 1 + 6 + 5 = 12 。
class Solution {
public int maxScore(int[] cardPoints, int k) {
int max = 0;
int sum = 0;
int n = cardPoints.length;
for (int i = 0; i < k; i++) {
sum = sum + cardPoints[i];
}
max = sum;
for (int j = 1; j <= k; j++) {
sum = sum - cardPoints[k - j] + cardPoints[n - j];
max = Math.max(max, sum);
}
return max;
}
}
1438. 绝对差不超过限制的最长连续子数组⭐
给你一个整数数组 nums ,和一个表示限制的整数 limit,请你返回最长连续子数组的长度,该子数组中的任意两个元素之间的绝对差必须小于或者等于 limit 。
如果不存在满足条件的子数组,则返回 0 。
解题思路:
当窗口内绝对差不超过 limit 时扩大窗口,当新加入窗口的元素使得绝对值之差超过 limit 时开始收缩窗口,窗口的最大宽度即最长子数组的长度。
但有个问题,当窗口进新元素时,我可以更新窗口中的最大值和最小值,但当窗口收缩时,如何更新最大值和最小值呢?难道要遍历一遍窗口中的所有元素吗?这
就用到单调队列结构了,这里需要一个通用的 MonotonicQueue 类,用来高效判断窗口中的最大值和最小值。
class Solution {
public int longestSubarray(int[] nums, int limit) {
int left = 0, right = 0;
int res = 0;
MyQueue window = new MyQueue();
while (right < nums.length) {
int c = nums[right];
right++;
window.add(c);
// 这里为什么用if呢?经过我举例观察发现:
// 在删除窗口左边元素时要么删掉的是最小值,要么是最大值。
// 并且最重要的是删掉之后两个单调队列里的最值就是相同的了。
if (window.max() - window.min() > limit) {
window.poll(nums[left]);
left++;
}
res = Math.max(res, right - left);
}
return res;
}
}
class MyQueue {
Deque<Integer> minDeque = new LinkedList<>();
Deque<Integer> maxDeque = new LinkedList<>();
void add(int val) {
while (!minDeque.isEmpty() && val < minDeque.getLast()) {
minDeque.removeLast();
}
minDeque.addLast(val);
while (!maxDeque.isEmpty() && val > maxDeque.getLast()) {
maxDeque.removeLast();
}
maxDeque.addLast(val);
}
void poll(int val) {
if (val == min()) {
minDeque.pollFirst();
}
if (val == max()) {
maxDeque.pollFirst();
}
}
int min() {
return minDeque.peek();
}
int max() {
return maxDeque.peek();
}
}
1658. 将 x 减到 0 的最小操作数⭐
给你一个整数数组 nums 和一个整数 x 。每一次操作时,你应当移除数组 nums 最左边或最右边的元素,然后从 x 中减去该元素的值。请注意,需要 修改 数组
以供接下来的操作使用。
如果可以将 x 恰好 减到 0 ,返回 最小操作数 ;否则,返回 -1 。
这道题需要转换一下思路,题目让你从边缘删除掉和为 x 的元素,那剩下来的是什么?剩下来的是不是就是 nums 中的一个子数组?让你尽可能少地从边缘删除
元素说明什么?是不是就是说剩下来的这个子数组大小尽可能的大?
所以,这道题等价于让你寻找 nums 中元素和为 sum(nums) - x 的最长子数组。
寻找子数组就是考察滑动窗口技巧。前文 滑动窗口框架 说过,使用滑动窗口算法需要搞清楚以下几个问题:
1、什么时候应该扩大窗口?
2、什么时候应该缩小窗口?
3、什么时候得到一个合法的答案?
针对本题,以上三个问题的答案是:
1、当窗口内元素之和小于目标和 target 时,扩大窗口,窗口内元素;
2、当窗口内元素之和大于目标和 target 时,缩小窗口,空余出更多可替换次数;
3、当窗口内元素之和等于目标和 target 时,找到一个符合条件的子数组,我们想找的是最长的子数组长度。
注意:类似 713. 乘积小于 K 的子数组,之所以本题可以用滑动窗口,关键是题目说了 nums 中的元素都是正数,这就保证了只要有元素加入窗口,和一定变大,
只要有元素离开窗口,和一定变小。
你想想如果存在负数的话就没有这个性质了,也就不能确定什么时候扩大和缩小窗口,也就不能使用滑动窗口算法。
而应该使用前缀和 + 哈希表的方式解决,参见 560. 和为K的子数组。
class Solution {
public int minOperations(int[] nums, int x) {
int n = nums.length, sum = 0;
for (int i = 0; i < n; i++) {
sum += nums[i];
}
// 滑动窗口需要寻找的子数组目标和
int target = sum - x;
int left = 0, right = 0;
// 记录窗口内所有元素和
int windowSum = 0;
// 记录目标子数组的最大长度
int maxLen = Integer.MIN_VALUE;
// 开始执行滑动窗口框架
while (right < nums.length) {
// 扩大窗口
windowSum += nums[right];
right++;
while (windowSum > target && left < right) {
// 缩小窗口
windowSum -= nums[left];
left++;
}
// 寻找目标子数组
if (windowSum == target) {
maxLen = Math.max(maxLen, right - left);
}
}
// 目标子数组的最大长度可以推导出需要删除的字符数量
return maxLen == Integer.MIN_VALUE ? -1 : n - maxLen;
}
}
动态规划
10. 正则表达式匹配
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
- '.' 匹配任意单个字符
- '*' 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
提示:
- 1 <= s.length <= 20
- 1 <= p.length <= 30
- s 只包含从 a-z 的小写字母。
- p 只包含从 a-z 的小写字母,以及字符 . 和 *。
- 保证每次出现字符 * 时,前面都匹配到有效的字符
class Solution {
public boolean isMatch(String s, String p) {
int m = s.length();
int n = p.length();
// dp[i][j]表示s的前i个字符和p的前j个字符是否匹配
boolean[][] dp = new boolean[m + 1][n + 1];
dp[0][0] = true;
// s为空,p不为空,由于*可以匹配0个字符,所以有可能为true。
// s = "",p = "a*b*c" 这种p的奇数索引位置上都是*字符的就可以和空串""匹配。
for (int i = 1; i <= n; i++) {
if (p.charAt(i - 1) == '*' && dp[0][i - 2]) {
dp[0][i] = true;
}
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if ((p.charAt(j - 1) == '.') || p.charAt(j - 1) == s.charAt(i - 1)) {
dp[i][j] = dp[i - 1][j - 1];
} else if (p.charAt(j - 1) == '*') {
// 若遇到*字符就拿*字符前面的那个字符p[j - 2]去和s[i - 1]匹配
// 若它们相等,或者p[j - 2]='.'就说明匹配上了
if (p.charAt(j - 2) == s.charAt(i - 1) || p.charAt(j - 2) == '.') {
// 匹配0个,或多次
dp[i][j] = dp[i][j - 2] || dp[i - 1][j];
} else {
// 若p[j - 2]和s[i - 1]不等
// 那*字符前面出现的字符就出现0次,匹配0次。
dp[i][j] = dp[i][j - 2];
}
}
}
}
return dp[m][n];
}
}
70. 爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
爬楼梯时注意题目给出所站的位置。
这道题就像是站在第1个楼梯下面,往上爬楼梯。
class Solution {
public int climbStairs(int n) {
if (n <= 1) {
return n;
}
int[] dp = new int[n + 1];
// dp[i]表示爬上第i个楼梯,需要几种方式。
// 题目给出了1 <= n <= 45的条件,所以说不用考虑dp[0]的情况。
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
}
746. 使用最小花费爬楼梯
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
输入:cost = [10,15,20]
输出:15
解释:你将从下标为 1 的台阶开始。
- 支付 15 ,向上爬两个台阶,到达楼梯顶部。总花费为 15 。
从例子可以看出是有下标为0的数组。
题目告诉了我们可以站在下标为0或者下标为1的楼梯上,开始爬楼梯。不同于70题,70题没有站在任何楼梯上。
class Solution {
public int minCostClimbingStairs(int[] cost) {
int dp[] = new int[cost.length + 1];
// dp[i]定义为爬上第i阶楼梯的最低花费
// 如果要爬完所有的楼梯那最小花费应该是dp[dp.length - 1]
dp[0] = 0; // 可以从第0阶或者第1阶开始爬,直接站在上面。离开楼梯时需要支付费用。
dp[1] = 0;
// 注意这里i < dp.length
for (int i = 2; i < dp.length; i++) {
dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
return dp[dp.length - 1];
}
}
53. 最大子数组和🌈
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
状态定义:
dp[i]:表示以 nums[i]结尾的连续子数组的最大和。
状态转移方程(描述子问题之间的联系):
根据状态的定义,由于 nums[i] 一定会被选取,并且以 nums[i] 结尾的连续子数组与以 nums[i - 1] 结尾的连续子数组只相差一个元素 nums[i] 。
假设数组 nums 的值全都严格大于 0,那么一定有 dp[i] = dp[i - 1] + nums[i]。
可是 dp[i - 1] 有可能是负数,于是分类讨论:
- 如果 dp[i - 1] > 0,那么可以把 nums[i] 直接接在 dp[i - 1] 表示的那个数组的后面,得到和更大的连续子数组;
- 如果 dp[i - 1] <= 0,那么 nums[i] 加上前面的数 dp[i - 1] 以后值不会变大。于是 dp[i] 「另起炉灶」,此时单独的一个 nums[i] 的值,就是 dp[i]。
以上两种情况的最大值就是 dp[i] 的值,写出如下状态转移方程:
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i])
初始值:
dp[0] 根据定义,只有 1 个数,一定以 nums[0] 结尾,因此 dp[0] = nums[0]。
输出:
这里状态的定义不是题目中的问题的定义,不能直接将最后一个状态返回回去。因为以nums[len - 1]结尾的连续子数组的和不一定是最大的。
而是返回dp数组中最大值。
class Solution {
public int maxSubArray(int[] nums) {
int len = nums.length;
int[] dp = new int[len];
dp[0] = nums[0];
int max = nums[0];
for (int i = 1; i < len; i++) {
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
max = Math.max(max, dp[i]);
}
return max;
}
}
152. 乘积最大子数组🌈
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
子数组 是数组的连续子序列。
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
class Solution {
// 参考:「力扣」第 53 题思路
public int maxProduct(int[] nums) {
int len = nums.length;
if (len == 1) {
return nums[0];
}
// 状态定义:以索引 i 结尾
// 思考清楚一种特例: [2, -1 ,3],前面乘起来是负数的话,倒不如另起炉灶
// maxDp[i]表示以nums[i]结尾的连续子序列的乘积的最大值。
int[] maxDp = new int[len];
// minDp[i]表示以nums[i]结尾的连续子序列的乘积的最小值。
int[] minDp = new int[len];
// 初始化两个dp数组
maxDp[0] = nums[0];
minDp[0] = nums[0];
int res = maxDp[0];
for (int i = 1; i < len; i++) {
// 遍历到nums[i]是正数时
if (nums[i] >= 0) {
maxDp[i] = Math.max(nums[i], maxDp[i - 1] * nums[i]);
minDp[i] = Math.min(nums[i], minDp[i - 1] * nums[i]);
} else {
maxDp[i] = Math.max(nums[i], minDp[i - 1] * nums[i]);
minDp[i] = Math.min(nums[i], maxDp[i - 1] * nums[i]);
}
res = Math.max(res, maxDp[i]);
}
return res;
}
}
62. 不同路径🍁
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
class Solution {
public int uniquePaths(int m, int n) {
//dp[i][j]: 表示从(0,0)出发,到(i,j) 有dp[i][j]条不同的路径。
int[][] dp = new int[m][n];
// 初始化,第一行的方格只有一种走法
for (int i = 0; i < m; i++) {
dp[i][0] = 1;
}
// 第一列的方格也只有一种走法
for (int i = 0; i < n; i++) {
dp[0][i] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
}
63. 不同路径 II🍁
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?

这题和上题不同的是我们在初始化base case时要考虑障碍物,遇到障碍物之后,障碍物所在的列和行不能在继续往后走了。
而且在状态转移时,遇到障碍物,障碍物所在的方块就达到不了。
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int n = obstacleGrid.length, m = obstacleGrid[0].length;
int[][] dp = new int[n][m];
// 下面两个for循环是初始化,当遇到障碍物时,这一行或者这一列后面的方格都到达不了。
for (int i = 0; i < m; i++) {
// 一旦遇到障碍,后续都到不了
if (obstacleGrid[0][i] == 1) {
break;
}
dp[0][i] = 1;
}
for (int i = 0; i < n; i++) {
// 一旦遇到障碍,后续都到不了
if (obstacleGrid[i][0] == 1) {
break;
}
dp[i][0] = 1;
}
for (int i = 1; i < n; i++) {
for (int j = 1; j < m; j++) {
if (obstacleGrid[i][j] == 1) {
// 从两个for循环的遍历顺序来看,是一行一行的处理的,当遇到一个障碍物,continue跳出内层循环
// 继续处理障碍物右边的方格。
continue;
}
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[n - 1][m - 1];
}
}
97. 交错字符串🍁
给定三个字符串 s1、s2、s3,请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。
两个字符串 s 和 t 交错 的定义与过程如下,其中每个字符串都会被分割成若干 非空 子字符串:
- s = s1 + s2 + ... + sn
- t = t1 + t2 + ... + tm
- |n - m| <= 1
- 交错 是 s1 + t1 + s2 + t2 + s3 + t3 + ... 或者 t1 + s1 + t2 + s2 + t3 + s3 + ...
注意:a + b 意味着字符串 a 和 b 连接。
参考题解:
class Solution {
public boolean isInterleave(String s1, String s2, String s3) {
int m = s1.length(), n = s2.length();
if (s3.length() != m + n) {
return false;
}
// 动态规划,dp[i,j]表示s1前i字符能与s2前j字符组成s3前i+j个字符。
boolean[][] dp = new boolean[m + 1][n + 1];
dp[0][0] = true;
// 只有s1字符串
for (int i = 1; i <= m && s1.charAt(i - 1) == s3.charAt(i - 1); i++) {
dp[i][0] = true; // 不相符直接终止
}
// 只有s2字符串
for (int j = 1; j <= n && s2.charAt(j - 1) == s3.charAt(j - 1); j++) {
dp[0][j] = true; // 不相符直接终止
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
dp[i][j] = (dp[i - 1][j] && s3.charAt(i + j - 1) == s1.charAt(i - 1)) ||
(dp[i][j - 1] && s3.charAt(i + j - 1) == s2.charAt(j - 1));
}
}
return dp[m][n];
}
}
91. 解码方法🍎
一条包含字母 A-Z 的消息通过以下映射进行了 编码 :
'A' -> "1"
'B' -> "2"
...
'Z' -> "26"
要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法)。例如,"11106" 可以映射为:
- "AAJF" ,将消息分组为 (1 1 10 6)
- "KJF" ,将消息分组为 (11 10 6)
注意,消息不能分组为 (1 11 06) ,因为 "06" 不能映射为 "F" ,这是由于 "6" 和 "06" 在映射中并不等价。
给你一个只含数字的 非空 字符串 s ,请计算并返回 解码 方法的 总数 。
题目数据保证答案肯定是一个 32 位 的整数。
提示:
- 1 <= s.length <= 100;
- s 只包含数字,并且可能包含前导零。
状态定义:
定义dp[i]为s的前i个字符解码方式的数量
状态转移:
1.如果s[i]不为0,则可以单独解码s[i],由于求的是方案数,如果确定了第i个数字的翻译方式,那么解码前i个数字和解码前i - 1个数的方案数就是相同的。
即f[i] = f[i - 1]。(s[]数组下标从1开始)。
2.将s[i]和s[i - 1]组合起来解码( 组合的数字范围在10 ~ 26之间 )。如果确定了第i个数和第i - 1个数的解码方式,那么解码前i个数字和解码前i - 2个数的方案数就
是相同的,即f[i] = f[i - 2]。(s[]数组下标从1开始)
初始化:
dp[0] = 1
为什么解码前0个数的方案数是1?
dp[0]代表前0个数字的方案数,这样的状态定义其实是没有实际意义的,但是dp[0]的值需要保证边界是对的,即dp[1]和dp[2]是对的。比如说,第一个数不为0,
那么解码前1个数只有一种方法,将其单独解码,即dp[1] = dp[1 - 1] = 1。解码前两个数,如果第1个数和第2个数可以组合起来解码。
那么dp[2] = dp[1] + dp[0] = 2 ,否则只能单独解码第2个数,即dp[2] = dp[1] = 1。
因此,在任何情况下dp[0]取1都可以保证dp[1]和dp[2]是正确的,所以dp[0]应该取1。
class Solution {
public int numDecodings(String s) {
int n = s.length();
// 定义:dp[i] 表示 s 的前 i 个字符解码方式的数量
int[] dp = new int[n + 1];
// base case: s 为空或者 s 只有一个字符的情况
dp[0] = 1;
// 注意有前导0的情况存在
dp[1] = s.charAt(0) == '0' ? 0 : 1;
// 注意 dp 数组和 s 之间的索引偏移一位
for (int i = 2; i <= n; i++) {
char c = s.charAt(i - 1), d = s.charAt(i - 2);
// 0 不能单独解码
if ('1' <= c && c <= '9') {
// 1. s[i] 本身可以作为一个字母
dp[i] += dp[i - 1];
}
// 如果c是1-9可以单独解码 这里dp[i]就已经包含之前的情况了。
// 如果还可以和前面一个数组合解码
if (d == '1' || d == '2' && c <= '6') {
// 2. s[i] 和 s[i - 1] 结合起来表示一个字母
dp[i] += dp[i - 2];
}
}
return dp[n];
}
}
剑指 Offer 46. 把数字翻译成字符串🍎
给定一个数字,我们按照如下规则把它翻译为字符串:0 翻译成 “a” ,1 翻译成 “b”,……,11 翻译成 “l”,……,25 翻译成 “z”。一个数字可能有多个翻译。请编程
实现一个函数,用来计算一个数字有多少种不同的翻译方法。
class Solution {
/**
* dp[i] 表示的是前i个数字的翻译方法数
* 分两种情况:
* 1. 第i位数字 无法和前面的数组合,比如 1245, 5 只能单独翻译,
* 那么方法数和 124 是一样的dp[i] = dp[i - 1]。
* 2.第i位数字 可以和前面的数组合,比如 1215, 5 可以选择 组合 和 不组合,最终结果为两种情况相加
* a. 选择组合,15看成是整体,那么 dp[i] = dp[i - 2]
* b. 不选择组合,5单独翻译,那么 dp[i] = dp[i - 1]
*/
public int translateNum(int num) {
String s = String.valueOf(num);
int n = s.length();
int[] dp= new int[n + 1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
char c = s.charAt(i - 1);
char d = s.charAt(i - 2);
if (c >= '0' && c <= '9') {
dp[i] = dp[i] + dp[i - 1];
}
if (d == '1' || d == '2' && c <= '5') {
dp[i] = dp[i] + dp[i - 2];
}
}
return dp[n];
}
}
64. 最小路径和🌻
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
状态定义:
设 dp为大小m×n 矩阵,其中dp[i] [j]的值代表直到走到 (i, j)的最小路fuhao径和。
转移方程:
只能向右或向下走,换句话说,当前单元格 (i, j)只能从左方单元格 (i, j - 1)或上方单元格 (i- 1, j)走到,因此只需要考虑矩阵左边界和上边界。
走到当前单元格 (i, j)的最小路径和 == “从左方单元格 (i-1, j)与 从上方单元格 (i, j-1)走来的两个最小路径和中较小的 ” + 当前单元格值grid[i] [j]。
具体分为以下4种情况:
- 当左边和上边都不是矩阵边界时: 即当i ≠ 0,j ≠ 0,dp[i] [j] = min(dp[i - 1] [j], dp[i] [j - 1]) + grid[i] [j];
- 当只有左边是矩阵边界时:只能从上面来,即当i = 0, j ≠ 0时,dp[i] [j] = dp[i] [j - 1] + grid[i] [j];
- 当只有上边是矩阵边界时:只能从上面来,即当i ≠ 0, j = 0时,dp[i] [j] = dp[i - 1] [j] + grid[i] [j];
- 当左边和上边都是矩阵边界时:即当i = 0,j = 0,其实就是起点,dp[i] [j] = grid[i] [j]。
初始状态:
dp 初始化即可,不需要修改初始0值。
返回值:
返回dp矩阵右下角值,即走到终点的最小路径和。
class Solution {
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int[][] dp = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (i == 0 && j == 0) {
dp[i][j] = grid[i][j];
} else if (i == 0 && j != 0) {
dp[i][j] = dp[i][j - 1] + grid[i][j];
} else if (j == 0 && i != 0) {
dp[i][j] = dp[i - 1][j] + grid[i][j];
} else {
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
}
}
return dp[m - 1][n - 1];
}
}
174. 地下城游戏🌻
一些恶魔抓住了公主(P)并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。
我们英勇的骑士(K)最初被安置在左上角的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);
其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快到达公主,骑士决定每次只向右或向下移动一步。
参考题解:https://labuladong.gitee.io/algo/3/28/87/
class Solution {
/* 主函数 */
int calculateMinimumHP(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
// 备忘录中都初始化为 -1
memo = new int[m][n];
for (int[] row : memo) {
Arrays.fill(row, -1);
}
return dp(grid, 0, 0);
}
// 备忘录,消除重叠子问题
int[][] memo;
// 定义:从 (i, j) 到达右下角,需要的初始血量至少是多少
int dp(int[][] grid, int i, int j) {
int m = grid.length;
int n = grid[0].length;
// base case
if (i == m - 1 && j == n - 1) {
return grid[i][j] >= 0 ? 1 : -grid[i][j] + 1;
}
if (i == m || j == n) {
return Integer.MAX_VALUE;
}
// 避免重复计算
if (memo[i][j] != -1) {
return memo[i][j];
}
// 状态转移逻辑
int res = Math.min(dp(grid, i, j + 1), dp(grid, i + 1, j)) - grid[i][j];
// 骑士的生命值至少为 1
memo[i][j] = res <= 0 ? 1 : res;
return memo[i][j];
}
}
dp数组写法:
96. 不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。

class Solution {
public int numTrees(int n) {
// dp[i]表示i个节点能够组成二叉搜索树的数量。
int[] dp = new int[n + 1];
// 初始化0个节点和1个节点的情况。
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= i; j++) {
// 对于第i个节点,需要考虑1作为根节点直到i作为根节点的情况,所以需要累加。
// 一共i个节点,对于根节点j时,左子树的节点个数为 j-1,右子树的节点个数为 i - j。
dp[i] += dp[j - 1] * dp[i - j]; // dp[2] = dp[0] * dp[1]
}
}
return dp[n];
}
}
0-1背包问题😭
二维dp写法:
public class Package01 {
public static void main(String[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
// 背包可装的最大重量
int bagWeight = 4;
int res = testWeightBagProblem(weight, value, bagWeight);
System.out.println("能获取的最大价值是:" + res);
}
public static int testWeightBagProblem(int[] weight, int[] value, int bagWeight) {
int wLen = weight.length;
// 定义dp数组:dp[i][j]表示背包容量为j时,前i个物品能获得的最大价值。
int[][] dp = new int[wLen][bagWeight + 1]; // 注意dp数组二维的大小,在重量基础上加一,因为我们要考虑背包能装的最小重量为0(base case)。
// 初始化:背包容量为0时,能获得的价值都为0。
for (int i = 0; i < wLen; i++) {
dp[i][0] = 0;
}
// 初始化:dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值,就是下标0的物体的价值。
// 那么显而易见只有背包容量大于weight[0](下标为0的物品重量)时才能装下它获取价值。
for (int j = weight[0]; j <= bagWeight; j++) {
dp[0][j] = value[0];
}
// 遍历顺序:先遍历物品,再遍历背包容量。
for (int i = 1; i < wLen; i++) {
for (int j = 1; j <= bagWeight; j++) {
// 选下标为i物品的前提背包剩余容量j >= weight[i]
// 若下标为i的物品大于背包允许的重量
if (weight[i] > j) {
dp[i][j] = dp[i - 1][j]; // weight[1] == 3 > j == 1 >>> dp[1][1] = dp[0][1]。
} else { // 容量足够时,但是也可以选第i件物品,也可以不选。
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
}
// 打印dp数组
for (int i = 0; i < wLen; i++) {
for (int j = 0; j <= bagWeight; j++) {
System.out.print(dp[i][j] + " ");
}
System.out.print("\n");
}
return dp[wLen - 1][bagWeight];
}
}
一维dp写法:
public class Package02 {
public static void main(String[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
// 背包可装的最大重量
int bagWeight = 4;
int res = testWeightBagProblem(weight, value, bagWeight);
System.out.println("能获取的最大价值是:" + res);
}
public static int testWeightBagProblem(int[] weight, int[] value, int bagWeight) {
int wLen = weight.length;
// 定义dp数组:dp[j]表示背包容量为j时,能获得的最大价值。
int[] dp = new int[bagWeight + 1];
// 对于初始化问题,dp[0] = 0是肯定可以确定地,因为背包的容量都是0,获取的最大价值肯定是0。
// 遍历顺序:先遍历物品,再遍历背包容量。
// 关于遍历顺序其实很有讲究的。
// 如果正序遍历背包容量,物品有可能被多次放入,就不满足每件物品只有一个的要求了。
// 当i = 0时,放第一件物品,当然物品要能够放到背包里,这个物品的重量是要小于背包容量的,这也是为什么内层循环 j >= weight[i]的原因。
// 若采用正序遍历:
// dp[1] = Math.max(dp[1], dp[0] + 15) == 15;
// dp[2] = Math.max(dp[2], dp[1] + 15) == 30; 这样物品0就放入了两次。 因为一个dp[j]状态的更新是要用到它左边的某个数dp[x]。
// 为什么倒序遍历就不会发生物品多次放入背包呢?
// 难道就是我们一维数组的状态转移不适合正序遍历吗?
// 倒序遍历时第一轮外循环结束,背包可容纳重量大于物品0重量 对应的最大价值就是物品0的价值。
for (int i = 0; i < wLen; i++) {
for (int j = bagWeight; j >= weight[i]; j--) {
// 当i = 0这一轮循环结束dp数组为[0, 15, 15, 15, 15]
// 接着下一轮循环i = 1,j = 4时 dp[4] = Math.max(dp[4], dp[4 - 3] + 20) = 35。
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
// 打印dp数组
for (int j = 0; j <= bagWeight; j++) {
System.out.print(dp[j] + " ");
}
return dp[bagWeight];
}
}
416. 分割等和子集⭐⭐
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
这题是需要转换为01背包问题。
做这道题需要做一个等价转换:是否可以从输入数组中挑选出一些正整数,使得这些数的和 等于 整个数组元素的和的一半。
那么相当于背包的容量是数组元素和的一半,定义为target。
数组中的每一个元素 i 相当于是一件物品,其重量是nums[i],价值也是nums[i]。
我们只需要看是否恰好有物品的重量加起来等于背包的可容纳重量,这题物品的重量和价值是同一个数,那么当刚好达到背包的可容纳重量,此时价值也最大。
价值之和就是重量之和,在不超过背包容量target的情况下,寻找最大价值。选取的物品总重量刚好等于target时,说明可以分割为等和子集。
其实就和背包问题一样在不超过背包容量时寻找最大价值。背包的总容量是限制,带着镣铐跳舞。
class Solution {
public boolean canPartition(int[] nums) {
int len = nums.length;
int sum = 0;
for (int num : nums) {
sum += num;
}
// 分成两个等和子集,那总和肯定是偶数啊。
if (sum % 2 == 1) {
return false;
}
int target = sum >> 1;
int[] dp = new int[target + 1];
// dp[j]代表总和为j时,最大可凑成的子集总和。
// 遍历顺序依然是先物品,再背包。
for (int i = 0; i < len; i++) {
for (int j = target; j >= nums[i]; j--) {
dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
}
}
return dp[target] == target;
}
}
1049. 最后一块石头的重量 II⭐⭐
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果 x == y,那么两块石头都会被完全粉碎;
- 如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
注意看题目的描述,当我们尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就转换为01背包问题了。
就是说在所有石头中选取一些石头,让这些石头重量之和最接近石头总重量的一半。
class Solution {
public int lastStoneWeightII(int[] stones) {
int len = stones.length;
int totalHeavy = 0;
for (int h : stones) {
totalHeavy += h;
}
int target = totalHeavy / 2;
// 就是让所选取石头重量之和最接近石头总重量的一半。(选取物品尽最大能力达到背包的最大容量)
// 背包不一定要装满。
// 然后用剩下的那堆没有选择的石头的重量减去选择石头的重量,就是最后剩下的重量。
int[] dp = new int[target + 1];
for (int i = 0; i < len; i++) {
for (int j = target; j >= stones[i]; j--) {
dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
//
return (totalHeavy - dp[target]) - dp[target];
}
}
494. 目标和⭐⭐⭐
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,nums = [2, 1] ,可以在 2 之前添加 '+' ,在 1 之前添加 '-' ,然后串联起来得到表达式 "+2-1" 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
解题思路:
原问题等同于: 找到nums一个正子集和一个负子集,使得总和等于target。
我们假设P是正子集,N是负子集 例如: 假设nums = [1, 2, 3, 4, 5],target = 3,一个可能的解决方案是+1-2+3-4+5 = 3 这里正子集P = [1, 3, 5]和负子集N = [2, 4]
那么让我们看看如何将其转换为子集求和问题:
sum(P) - sum(N) = target
sum(P) + sum(N) + sum(P) - sum(N) = target + sum(P) + sum(N)
2 * sum(P) = target + sum(nums)
因此,原来的问题已转化为一个求子集的和问题: 找到nums的一个子集 P,使得sum(P) = (target + sum(nums)) / 2 背包容量
请注意,上面的公式已经证明target + sum(nums)必须是偶数。
class Solution {
public int findTargetSumWays(int[] nums, int target) {
target = Math.abs(target);
int sum = 0;
// 求出数组总和,数组中所有元素都是正的。
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
}
// target + sum 一定是偶数
if ((target + sum) % 2 != 0) {
return 0;
}
int size = (target + sum) / 2;
// dp[j] 表示:填满j(包括j)这么大容积的包,有dp[j]种方法。
int[] dp = new int[size + 1];
// dp[0] = 1,理论上也很好解释,装满容量为0的背包,有1种方法,就是装0件物品。
dp[0] = 1;
// dp数组初始值为[1, 0, 0, 0, 0]
// i = 0第一轮外循环拿物品0去装入各背包 [1, 1, 0, 0, 0]
// dp[1] = dp[1] + dp[1 - nums[0]] = dp[0] = 1 代表的意思是把物品0装入容量为1的背包,
// 这时候使容量为1的背包装满的方法数和把背包总容量减去物品0的重量所剩余得容量装满的方法数一样。
// i = 0第一轮外循环结束时dp数组为 [1, 1, 0, 0, 0] 可以看到只得出了dp[1]的值其余dp[x] = dp[x - 1]都是0。
// i = 1第二轮外循环拿物品1去装入各背包 到dp[2]时,dp[2] = dp[2] + dp[2 - nums[1]] = dp[2 - 1] = 1。
// 到dp[1]时,dp[1] = dp[1] + dp[1 - nums[1]] = dp[1] + dp[0] = 2。更新dp[1]在原来dp[1]加上dp[0]。
// 因为我们的dp[j]代表容量为j的背包被装满有多少种方法。
for (int i = 0; i < nums.length; i++) {
for (int j = size; j >= nums[i]; j--) {
dp[j] += dp[j - nums[i]];
}
}
return dp[size];
}
}
474. 一和零(两个0-1背包)⭐⭐⭐
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
这道题怎么转换为01背包问题,首先这是一个二维的01背包,并不是多重背包,因为字符串数组中的字符串每一个都只能选择一次。
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
// dp[i][j]表示背包(字符串组合)两个维度的容量为i和j时,能获得的最大价值(字符串组合的长度最长(个数最多))
// 说白了就是在一个字符串数组(物品集合)中选一些字符串(物品)在不超过背包容量的限制下,能获得的最大价值。
// 一个物品(字符串)的价值就是1。
int[][] dp = new int[m + 1][n + 1];
int zeroNum = 0, oneNum = 0;
// 字符串数组的每一个元素相当于是物品
for (String str : strs) {
zeroNum = 0;
oneNum = 0;
for (char ch : str.toCharArray()) {
if (ch == '0') {
zeroNum++;
} else {
oneNum++;
}
}
// 在上面首先求出每一个物品(字符串数组中的字符串)0的数量和1的数量。
// 这两个数量相当于是物品的重量。
// 倒序遍历,m和n相当于是两个背包的容量。
// i >= zeroNum,j >= oneNum 容量肯定要大于物品重量时才考虑放入物品。
for (int i = m; i >= zeroNum; i--) {
for (int j = n; j >= oneNum; j--) {
dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
}
}
}
return dp[m][n];
}
}
完全背包
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪
些物品装入背包里物品价值总和最大。完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
背包最大重量为4。
物品为:
| 物品 | 重量 | 价值 |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
public class CompletePackageProblem {
public static void main(String[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWeight = 4;
int res = testCompletePack(weight, value, bagWeight);
System.out.println("能获取的最大价值是:" + res);
//testCompletePackAnotherWay();
}
// 先遍历物品,再遍历背包
private static int testCompletePack(int[] weight, int[] value, int bagWeight) {
int[] dp = new int[bagWeight + 1];
for (int i = 0; i < weight.length; i++) { // 遍历物品
for (int j = weight[i]; j <= bagWeight; j++) { // 遍历背包容量
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
return dp[bagWeight];
}
// 先遍历背包,再遍历物品
private static void testCompletePackAnotherWay() {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWeight = 4;
int[] dp = new int[bagWeight + 1];
for (int i = 1; i <= bagWeight; i++) { // 遍历背包容量
for (int j = 0; j < weight.length; j++) { // 遍历物品
if (i - weight[j] >= 0) {
dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);
}
}
}
}
}
其实还有一个很重要的问题,为什么遍历物品在外层循环,遍历背包容量在内层循环?
这个问题很多题解关于这里都是轻描淡写就略过了,大家都默认 遍历物品在外层,遍历背包容量在内层,好像本应该如此一样,那么为什么呢?
难道就不能遍历背包容量在外层,遍历物品在内层?
在完全背包中,对于一维dp数组来说,其实两个for循环嵌套顺序同样无所谓!
因为dp[j] 是根据下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以了。
518. 零钱兑换 II(遍历顺序)⭐⭐⭐
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
一看就是完全背包问题
class Solution {
public int change(int amount, int[] coins) {
// 我理解的背包问题就是在一个限制条件下完成某个目标。
// 限制条件就是抽象出来的背包容量,比如这里背包容量就是amount总金额
//
//递推表达式
// dp[j]表示凑成总金额j的硬币组合数
int[] dp = new int[amount + 1];
//初始化dp数组,表示金额为0时只有一种情况,也就是什么都不装。
dp[0] = 1;
for (int i = 0; i < coins.length; i++) {
for (int j = coins[i]; j <= amount; j++) {
dp[j] = dp[j] + dp[j - coins[i]];
}
}
return dp[amount];
}
}
在求装满背包有几种方案的时候,认清遍历顺序是非常关键的。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
377. 组合总和 Ⅳ⭐⭐⭐⭕
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围。
nums = [1, 2, 3] target = 4
所有可能的组合为: (1, 1, 1, 1) (1, 1, 2) (1, 2, 1) (1, 3) (2, 1, 1) (2, 2) (3, 1)
请注意,顺序不同的序列被视作不同的组合。
因此输出为 7。
本题题目描述说是求组合,但又说是可以元素相同顺序不同的组合算两个组合,其实就是求排列!
弄清什么是组合,什么是排列很重要。
组合不强调顺序,(1,5)和(5,1)是同一个组合。
排列强调顺序,(1,5)和(5,1)是两个不同的排列。
class Solution {
public int combinationSum4(int[] nums, int target) {
// dp[i]: 凑成目标正整数为i的排列个数为dp[i]
int[] dp = new int[target + 1];
// 因为题目中也说了:给定目标值是正整数! 所以dp[0] = 1是没有意义的,仅仅是为了推导递推公式。
dp[0] = 1;
// 先遍历背包
for (int i = 1; i <= target; i++) {
// 再遍历物品
for (int j = 0; j < nums.length; j++) {
// 背包容量肯定要大于物品容量才行
if (i >= nums[j]) {
dp[i] = dp[i] + dp[i - nums[j]];
}
}
}
return dp[target];
}
}
爬楼梯(进阶版)⭕
一步一个台阶,两个台阶,三个台阶,.......,直到 m个台阶。问有多少种不同的方法可以爬到楼顶呢?
1阶,2阶,.... m阶就是物品,楼顶就是背包。
每一阶可以重复使用,例如跳了1阶,还可以继续跳1阶。
问跳到楼顶有几种方法其实就是问装满背包有几种方法。
此时大家应该发现这就是一个完全背包问题了!
1.确定dp数组以及下标的含义
dp[i]:爬到有i个台阶的楼顶,有dp[i]种方法。
class Solution {
public int climbStairs(int n) {
int[] dp = new int[n + 1];
int[] weight = {1, 2}; // 物品
dp[0] = 1;
for (int i = 0; i <= n; i++) { // 先遍历背包
for (int j = 0; j < weight.length; j++) { // 再遍历物品
if (i >= weight[j]) dp[i] += dp[i - weight[j]];
}
}
return dp[n];
}
}
322. 零钱兑换⭐⭐⭐🎈
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
class Solution {
public int coinChange(int[] coins, int amount) {
int max = Integer.MAX_VALUE;
// dp[j]代表凑足总额为j所需硬币的最少个数。
int[] dp = new int[amount + 1];
// 初始化dp数组为最大值
for (int j = 0; j < dp.length; j++) {
dp[j] = max;
}
// 当金额为0时需要的硬币数目为0,题目给了用例amount = 0时,所需硬币数为0。
dp[0] = 0;
for (int i = 0; i < coins.length; i++) {
// 正序遍历:完全背包每个硬币可以选择多次
for (int j = coins[i]; j <= amount; j++) {
// 只有dp[j-coins[i]]不是初始最大值时,该位才有选择的必要。
// 该位不为max才说明容量为j - coins[i]时,有选择物品的方法将容量为j - coins[i]装满。
if (dp[j - coins[i]] != max) {
// 选择硬币数目最小的情况
dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
}
}
}
return dp[amount] == max ? -1 : dp[amount];
}
}
279. 完全平方数⭐⭐⭐🎈
给你一个整数 n ,返回和为 n 的完全平方数的最少数量。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
我来把题目翻译一下:完全平方数就是物品(可以无限件使用),凑够正整数n就是背包,问凑满这个背包最少有多少物品?
class Solution {
public int numSquares(int n) {
int max = Integer.MAX_VALUE;
// dp[j]表示和为j的完全平方数的最少数量
int[] dp = new int[n + 1];
for (int i = 0; i <= n; i++) {
dp[i] = max;
}
dp[0] = 0;
// 小于n的完全平方数就是物品
// 遍历物品
for (int i = 0; i * i <= n; i++) {
// 遍历背包
for (int j = i * i; j <= n; j++) {
if (dp[j - i * i] != max) {
dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
}
}
}
return dp[n];
}
}
139. 单词拆分⭐
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
确定dp数组以及下标的含义:
dp[i]表示长度为i的字符串可以拆分成一个或多个在字典里出现的单词。
状态转移:
如果确定dp[j] 是true,且 [j, i] 这个区间的子串出现在字典里,那么dp[i]一定是true。(j < i )。
所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。
初始化:
从递归公式中可以看出,dp[i] 的状态依靠 dp[j]是否为true,那么dp[0]就是递归的根基,dp[0]一定要为true,否则递归下去后面都都是false了。
那么dp[0]有没有意义呢?
dp[0]表示如果字符串为空的话,说明出现在字典里。
但题目中说了“给定一个非空字符串 s” 所以测试数据中不会出现i为0的情况,那么dp[0]初始为true完全就是为了推导公式。
下标非0的dp[i]初始化为false,只要没有被覆盖说明都是不可拆分为一个或多个在字典中出现的单词。
遍历顺序:
题目中说是拆分为一个或多个在字典中出现的单词,所以这是完全背包。
还要讨论两层for循环的前后循序。
- 如果求组合数就是外层for循环遍历物品,内层for遍历背包;
- 如果求排列数就是外层for遍历背包,内层for循环遍历物品。
但本题还有特殊性,因为是要求子串,最好是遍历背包放在外循环,将遍历物品放在内循环。
如果要是外层for循环遍历物品,内层for遍历背包,就需要把所有的子串都预先放在一个容器里。(如果不理解的话,可以自己尝试这么写一写就理解了)
所以最终我选择的遍历顺序为:遍历背包放在外循环,将遍历物品放在内循环。内循环从前到后。
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
int len = s.length();
// 字典里面的字符串就是物品,字符串s是背包。
// dp[i]表示长度为i的字符串可以拆分成一个或多个在字典里出现的单词。
boolean[] dp = new boolean[s.length() + 1];
dp[0] = true;
// 先遍历背包
for (int i = 1; i <= len; i++) {
// 再遍历物品
// 假设现在背包容量是4,体现在leet。
// 此时第一件物品是leet,第二件物品是eet,第三件物品是et,第四件物品是t。
// 当我们判断到leet在字典中,并且dp[0] = true那么dp[4] = true。
for (int j = 0; j < i; j++) {
if (wordDict.contains(s.substring(j, i)) && dp[j]) {
dp[i] = true;
break; // 找到一种由字典中的字符串拼接出的长度为i的字符串的方法就可以退出内循环。
}
}
}
return dp[len];
}
}
118. 杨辉三角
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和上方的数的和。
class Solution {
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> res = new ArrayList<>();
int[][] dp = new int[numRows + 1][numRows + 1];
for (int i = 1; i <= numRows; i++) {
List<Integer> temp = new ArrayList<>();
for (int j = 1; j <= i; j++) {
if (j == 1 || i == j) {
dp[i][j] = 1;
} else {
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
}
temp.add(dp[i][j]);
}
res.add(temp);
}
return res;
}
}
198. 打家劫舍⭐
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻
的房屋在同一晚上被小偷闯入,系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最
高金额。
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
class Solution {
public int rob(int[] nums) {
if (nums.length == 1) {
return nums[0];
}
int[] dp = new int[nums.length];
// dp[i]定义为考虑到下标i为止(包括下标i)的房屋,最多可以偷窃到的金额是dp[i]。
dp[0] = nums[0];
// 若第一间房屋金额多,偷第一间房屋。第二件房屋不偷。此时偷到的最高金额是nums[0]
// 若第二间房屋金额多,偷第二间房屋。第一间房屋不偷。此时偷到的最高金额是nums[1]
dp[1] = Math.max(nums[0], nums[1]);
for (int i = 2; i < nums.length; i++) {
// 状态转移方程可以如下理解:
// 1、如果偷第i间房屋,那么第i - 1间房屋是肯定不能偷的。此时偷取金额是到i - 2下标为止的房屋,能偷取的金额加上偷i间房屋的金额
// 2、如果不偷第i间房屋,能偷取到的金额就是以i - 1下标为止的房屋,能够偷取到的金额。
dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[nums.length - 1];
}
}
213. 打家劫舍 II⭐
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。
同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
输入:nums = [2,3,2]
输出:3
解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
对于一个数组,成环的话主要有如下三种情况:
- 情况一:考虑不包含首尾元素
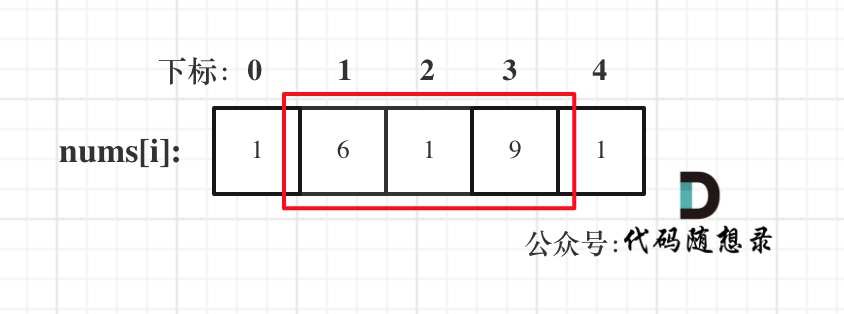
- 情况二:考虑包含首元素,不包含尾元素
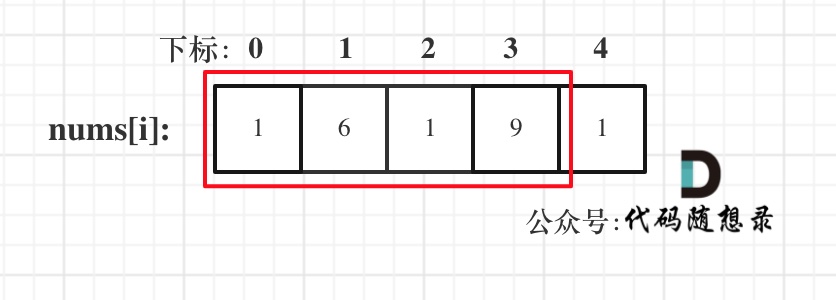
- 情况三:考虑包含尾元素,不包含首元素
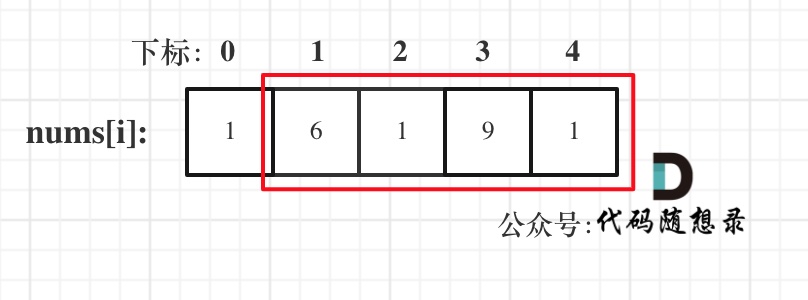
注意我这里用的是"考虑",例如情况三,虽然是考虑包含尾元素,但不一定要选尾部元素! 对于情况三,取nums[1] 和 nums[3]就是最大的。
而情况二 和 情况三 都包含了情况一了,所以只考虑情况二和情况三就可以了。
分析到这里,本题其实比较简单了。 剩下的和198.打家劫舍 (opens new window)就是一样的了。
class Solution {
public int rob(int[] nums) {
int res1 = robRange(nums, 0, nums.length - 2);
int res2 = robRange(nums, 1, nums.length - 1);
return Math.max(res1, res2);
}
public int robRange(int[] nums, int start, int end) {
// 注意考虑如下的特殊情况
// 当数组元素只有一个时,直接返回这个数
if (nums.length == 1) {
return nums[0];
}
// 当数组只有两个元素时,比如[2, 3],robRange(nums, 0, 0)返回2,robRange(nums, 1, 1)返回3。
if (start == end) {
return nums[start];
}
int[] dp = new int[nums.length];
dp[start] = nums[start];
dp[start + 1] = Math.max(nums[start], nums[start + 1]);
for (int i = start + 2; i <= end; i++) {
dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1]);
}
// 这里是返回dp[end],因为end无论在那一段都是最后需要考虑的,end有可能是nums.length - 1,有可能是nums.length - 2。
return dp[end];
}
}
337. 打家劫舍 III⭐
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相
连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额。
这道题是树形dp入门问题,仔细分析下。
参考题解:https://leetcode.cn/problems/house-robber-iii/solution/shu-xing-dp-ru-men-wen-ti-by-liweiwei1419/
状态定义:
dp[node] [j] :这里 node 表示一个结点,以 node 为根结点的树,并且规定了 node 是否偷取能够获得的最大价值。
- j = 0 表示 node 结点不偷取;
- j = 1 表示 node 结点偷取。
状态转移:
根据当前结点偷或者不偷,就决定了需要从哪些子结点里的对应的状态转移过来。
- 如果当前结点不偷,左右子结点偷或者不偷都行,选最大者;
- 如果当前结点偷,左右子结点均不能偷。
初始化:
一个结点都没有,空节点,返回 0,对应后序遍历时候的递归终止条件。
输出:
在根结点的时候,返回两个状态的较大者。
class Solution {
// 树的后序遍历(递归写法) 左右中
public int rob(TreeNode root) {
int[] res = dfs(root);
return Math.max(res[0], res[1]);
}
private int[] dfs(TreeNode node) {
if (node == null) {
return new int[]{0, 0};
}
// 分类讨论的标准是:当前结点偷或者不偷
// 由于需要后序遍历,所以先计算左右子结点,然后计算当前结点的状态值。
int[] left = dfs(node.left);
int[] right = dfs(node.right);
// dp[0]:以当前 node 为根结点的子树能够偷取的最大价值,规定 node 结点不偷。
// dp[1]:以当前 node 为根结点的子树能够偷取的最大价值,规定 node 结点偷。
int[] dp = new int[2];
dp[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
dp[1] = node.val + left[0] + right[0];
return dp;
}
}
343. 整数拆分
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回你可以获得的最大乘积。
121. 买卖股票的最佳时机⭐
1、确定dp数组以及下标的含义
- dp[i] [0]代表第i天持有股票的最大收益;
- dp[i] [1]代表第i天不持有股票的最大收益。
这道题dp数组的下标是和原price数组下标对应起来的,也就是说price下标对应元素属于我们定义的状态。
2、确定递推公式
如果第i天持有股票即dp[i] [0], 那么可以由两个状态推出来
- 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1] [0];
- 第i天买入股票,所得现金就是买入今天的股票后所得现金即:-prices[i]。
那么dp[i] [0]应该选所得现金最大的,所以dp[i] [0] = max(dp[i - 1] [0], -prices[i])
如果第i天不持有股票即dp[i] [1], 也可以由两个状态推出来
- 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1] [1]
- 第i天卖出股票,所得现金就是按照今天股票佳价格卖出后所得现金即:prices[i] + dp[i - 1] [0]
同样dp[i] [1]取最大的,dp[i] [1] = max(dp[i - 1] [1], prices[i] + dp[i - 1] [0]);
这样递归公式我们就分析完了
3、dp数组如何初始化
由递推公式 dp[i] [0] = max(dp[i - 1] [0], -prices[i]); 和 dp[i] [1] = max(dp[i - 1] [1], prices[i] + dp[i - 1] [0]);可以看出
其基础都是要从dp[0] [0]和dp[0] [1]推导出来。
那么dp[0] [0]表示第0天持有股票,此时的持有股票就一定是买入股票了,因为不可能有前一天推出来,所以dp[0] [0] -= prices[0];
dp[0] [1]表示第0天不持有股票,不持有股票那么现金就是0,所以dp[0] [1] = 0;
class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
int[][] dp = new int[len][2];
// 第0天就买入股票,此时的收益就是-prices[0]
dp[0][1] = -prices[0];
// 第0天未持有股票,只能是未买入,此时默认收益就是0
dp[0][0] = 0;
for (int i = 1; i < len; i++) {
// 第i天持有股票时的最大收益实际上就是看哪天买入价格更低
dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);
// 第i天未持有股票有两种情况
// 1.到第i天还未买入股票
// 2.第i天之前已经将股票卖出
// 对于第一种情况,还未买入股票,说明如果在前面几天买入股票再卖出利润都为负,根本不赚钱
// 在第i天时,判断卖出之前买入的股票收益与未买入股票的收益谁更高。
// 第二种情况比较之前已经卖出了股票的收益与第i天卖出股票的收益 较 (就是看与第i天之前最低的买入股票价格与卖出股票价格之差谁更大)
// 有可能第i天股票价格高,比之前卖出收益都更大。
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
}
return dp[len - 1][0];
}
}
122. 买卖股票的最佳时机 II⭐
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候最多只能持有一股股票。你也可以先购买,然后在同一天出售。
返回你能获得的最大利润。
这道题的题意是不限制买卖的次数,最终可以获得的最大利润。可以在同一天先卖出股票然后再买入股票。
第一种解法:贪心算法
class Solution {
public int maxProfit(int[] prices) {
int profit = 0;
for (int i = 1; i < prices.length; i++) {
int tmp = prices[i] - prices[i - 1];
if (tmp > 0) {
profit += tmp;
}
}
return profit;
}
}
第二种解法:动态规划
这道题与上面那道题的区别是,这题可以买卖多次,不只是买卖一次。
那么第i天持有股票时的收益(实际上是比较最低的买入价格)就是之前卖出股票所得的收益减去第i天股票价格。
class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
int[][] dp = new int[len][2];
dp[0][0] = 0;
dp[0][1] = -prices[0];
for (int i = 1; i < len; i++) {
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
}
return dp[len - 1][0];
}
}
123. 买卖股票的最佳时机 III⭐
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成两笔交易。
注意:你不能同时参与多笔交易(你必须再次购买前出售掉之前的股票)。
输入:prices = [3,3,5,0,0,3,1,4]
输出:6
解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。
随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
int[][] dp = new int[len][5];
// 第0天没有操作
dp[0][0] = 0;
// 第0天第一次买入股票收益
dp[0][1] = -prices[0];
// 第0天第一次卖出股票收益
dp[0][2] = 0;
// 第0天第二次买入股票收益
dp[0][3] = -prices[0];
// 第0天第二次卖出股票收益
dp[0][4] = 0;
for(int i = 1; i < len; i++){
dp[i][0] = dp[i - 1][0];
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
}
return dp[len - 1][4];
}
}
188. 买卖股票的最佳时机 IV⭐
给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
这道题思路和股票第三题是一样的,虽然不知道k具体是几次,但是也有章法可循。
class Solution {
public int maxProfit(int k, int[] prices) {
if (k == 0 || prices == null || prices.length <= 1) {
return 0;
}
int[][] dp = new int[prices.length][k * 2 + 1];
for (int i = 0; i < k * 2 + 1; i++) {
// 奇数买入
if (i % 2 == 1) {
dp[0][i] = -prices[0];
} else {
// 偶数卖出
dp[0][i] = 0;
}
}
for (int i = 1; i < prices.length; i++) {
// 最后j肯定是取到2k,是一个偶数。
for (int j = 1; j < k * 2 + 1; j++) {
// 奇数买入
if (j % 2 == 1) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - 1] - prices[i]);
} else {
// 偶数卖出
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - 1] + prices[i]);
}
}
}
return dp[prices.length - 1][2 * k];
}
}
309. 最佳买卖股票时机含冷冻期⭐
给定一个整数数组prices,其中第 prices[i] 表示第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
解题思路:由题意知,冷冻期是不持有股票的,更不能买入股票。
状态定义:
dp[i] [j] 表示在第i天,状态为j时,我们手上拥有的现金数。
具体有如下3个状态:
- 0表示今天不是卖出了股票的不持股状态;
- 1表示持股;
- 2表示今天由于卖出了股票的不持股状态。
状态转移方程:
1、0状态的转移
| 昨天 | 今天 | 分析是否可以转移,可以转移的情况下今天的操作 |
|---|---|---|
| 0 | 0 | 可以转移,今天什么都不做,沿用昨天的状态。 |
| 0 | 1 | 可以转移,今天买入股票。 |
| 0 | 2 | 不可以转移,不持股的情况下,不能卖出股票。 |
2、1状态的转移
| 昨天 | 今天 | 分析是否可以转移,可以转移的情况下今天的操作 |
|---|---|---|
| 1 | 0 | 不可以转移,根据我们的状态定义,只能转移到状态2。 |
| 1 | 1 | 可以转移,今天什么都不做,沿用昨天的状态。 |
| 1 | 2 | 可以转移,卖出股票进入不持股状态2. |
3、2状态的转移
| 昨天 | 今天 | 分析是否可以转移,可以转移的情况下今天的操作 |
|---|---|---|
| 2 | 0 | 可以转移,根据题意,今天就是冷冻期,什么都不能操作,进入状态0。 |
| 2 | 1 | 不可以转移,根据题意,昨天刚刚卖出股票,今天不能执行买入操作。 |
| 2 | 2 | 不可以转移,不持股的情况下,不能卖出股票。 |
初始化:
dp[0] [0] = 0,dp[0] [1] = -prices[0],dp[0] [2] = 0;
输出:
最后一天共有两种不持股的状态:
- 倒数第2天卖出,最后一天是冷冻期不持股;
- 最后一天卖出之后不持股。
那么收益最大是这两种状态的收益的最大值。
class Solution {
public int maxProfix(int[] prices) {
int len = prices.length;
int[][] dp = new int[len][3];
dp[0][0] = 0;
dp[0][1] = -prices[i];
dp[0][2] = 0;
for (int i = 1; i < len; i++) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][2]);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
dp[i][2] = dp[i - 1][1] + prices[i];
}
return Math.max(dp[len - 1][0], dp[len - 1][2]);
}
}
714. 买卖股票的最佳时机含手续费⭐
给定一个整数数组 prices,其中 prices[i]表示第 i 天的股票价格 ;整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易,但是你每笔交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
注意:这里的一笔交易指买入持有并卖出股票的整个过程,每笔交易你只需要为支付一次手续费。
做题时我们规定在买入股票时交手续费,当让也可以规定在卖出股票时交手续费。
状态定义:
- dp[i] [j] 表示:[0, i] 区间内,到下标为 i 这一天天(从 00 开始)状态为 j 时的我们手上拥有的现金数;
- 其中 j 取两个值:0 表示不持股,1 表示持股。
状态转移方程:
dp[i] [0]:当天不持股,可以由昨天不持股和昨天持股转换而来。
- 如果昨天不持股,今天仍然不持股,则说明今天什么都没做;
- 如果昨天持股,今天不持股,则说明今天卖出了一股,当前的 dp 应该加上当天的股价。
因此:dp[i] [0] = max(dp[i - 1] [0], dp[i - 1] [1] + prices[i])。
dp[i] [1]:当天持股,也可以由昨天不持股和昨天持股转换而来。
- 如果昨天不持股,今天持股,则说明今天买入股票,根据我们之前的规定,需要扣除手续费;
- 如果昨天持股,今天仍然持股,则说明今天什么都没做。
因此:dp[i] [1] = max(dp[i - 1] [1], dp[i - 1] [0] - prices[i] - fee)。
初始化:
dp[0] [0] = 0,dp[0] [1] = -prices[i] - fee。
输出:
每一天都由前面几天的状态转换而来,最优值在最后一天,并且是不持股的状态。
class Solution {
public int maxProfit(int[] prices, int fee) {
int len = prices.length;
int[][] dp = new int[len][2];
dp[0][0] = 0;
dp[0][1] = -prices[i] - fee;
for (int i = 1; i < len; i++) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i] - fee);
}
return dp[len - 1][0];
}
}
300. 最长递增子序列的长度⭐⭐⭐🍓
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
这道题是很经典「动态规划」算法问题。
- 需要对「子序列」和「子串」这两个概念进行区分;
- 子序列:子序列并不要求连续;
- 子串:子串一定是原始字符串的连续子串。
- 题目中的「上升」的意思是「严格上升」;
- 子序列中元素的相对顺序很重要,子序列中的元素必须保持在原始数组中的相对顺序。如果把这个限制去掉,将原始数组去重以后,元素的个数即为所求。
算法实现步骤
-
确定dp数组以及下标含义;
dp[i]表示以nums[i]结尾的最长递增子序列的长度
-
状态转移方程;
如果一个较大的数接在较小的数后面,就会形成一个更长的子序列。只要 nums[i] 严格大于在它位置之前的某个数。
那么 nums[i] 就可以接在这个数后面形成一个更长的上升子序列。
-
初始化;
dp[i] = 1,1个字符显然是长度为 1 的上升子序列。
-
输出;
不能返回最后一个状态值,最后一个状态值只表示以 nums[len - 1] 结尾的「上升子序列」的长度,状态数组 dp 的最大值才是题目要求的结果。
-
空间优化。
遍历到一个新数的时候,之前所有的状态值都得保留,因此无法优化空间。
class Solution {
public int lengthOfLIS(int[] nums) {
int[] dp = new int[nums.length];
// base case 每个字符都可以单独构成一个长度的上升子序列。
Arrays.fill(dp, 1);
int res = 0;
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[j] + 1, dp[i]);
}
}
res = Math.max(res, dp[i]);
}
return res;
}
}
354. 俄罗斯套娃信封问题🍓
给你一个二维整数数组 envelopes ,其中 envelopes[i] = [wi, hi] ,表示第 i 个信封的宽度和高度。
当另一个信封的宽度和高度都比这个信封大的时候,这个信封就可以放进另一个信封里,如同俄罗斯套娃一样。
请计算 最多能有多少个 信封能组成一组“俄罗斯套娃”信封(即可以把一个信封放到另一个信封里面)。
注意:不允许旋转信封。
这道题的解法比较巧妙:
先对宽度 w 进行升序排序,如果遇到 w 相同的情况,则按照高度 h 降序排序;之后把所有的 h 作为一个数组,在这个数组上计算 LIS 的长度就是答案。
画个图理解一下,先对这些数对进行排序:

然后在 h 上寻找最长递增子序列,这个子序列就是最优的嵌套方案:
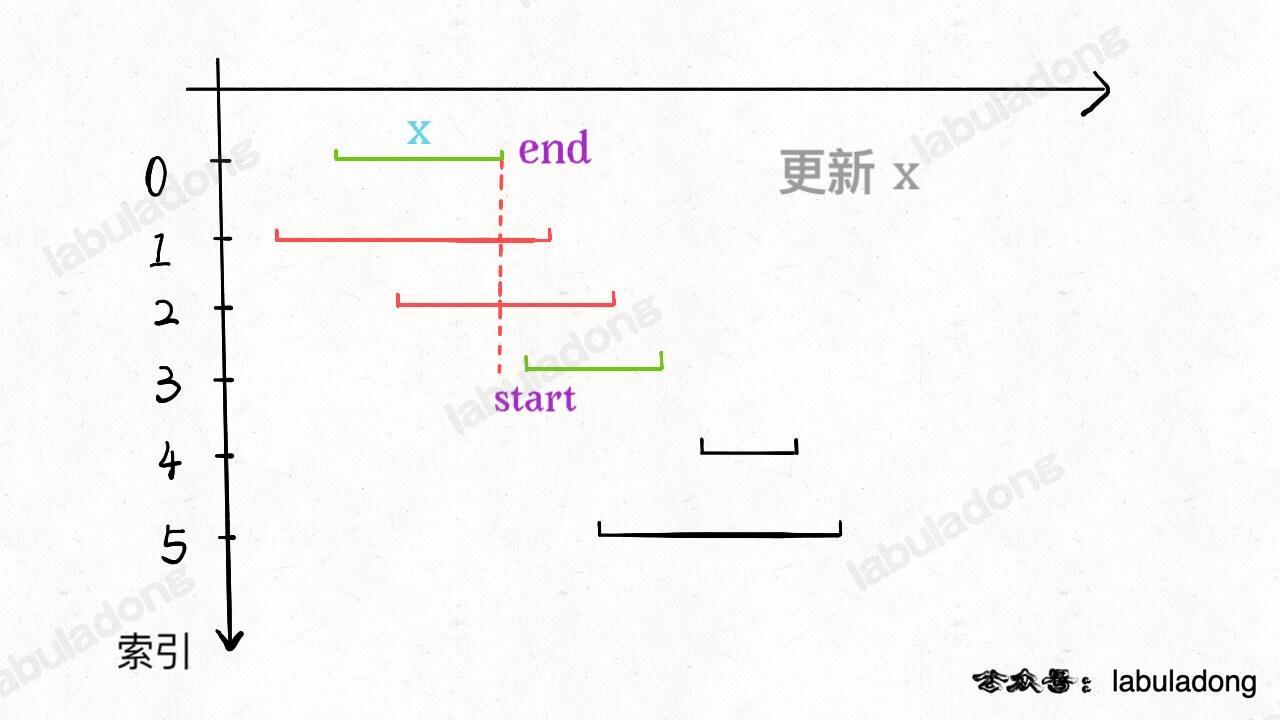
为什么呢?稍微思考一下就明白了:
首先,对宽度 w 从小到大排序,确保了 w 这个维度可以互相嵌套,所以我们只需要专注高度 h 这个维度能够互相嵌套即可。
其次,两个 w 相同的信封不能相互包含,所以对于宽度 w 相同的信封,对高度 h 进行降序排序,保证 LIS 中不存在多个 w 相同的信封(因为题目说了长宽相同
也无法嵌套)。
class Solution {
public int maxEnvelopes(int[][] envelopes) {
Arrays.sort(envelopes, (a, b) -> {
if (a[0] == b[0]) {
return b[1] - a[1];
} else {
return a[0] - b[0];
}
});
int n = envelopes.length;
int[] height = new int[n];
for (int i = 0; i < n; i++) {
height[i] = envelopes[i][1];
}
int res = lengthOfLIS(height);
return res;
}
private int lengthOfLIS(int[] height) {
int n = height.length;
int[] dp = new int[n];
Arrays.fill(dp, 1);
int res = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < i; j++) {
if (height[i] > height[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
res = Math.max(res, dp[i]);
}
return res;
}
}
上面解法已经超时了
下面这种二分方法能过
class Solution {
public int maxEnvelopes(int[][] envelopes) {
int n = envelopes.length;
Arrays.sort(envelopes, (e1, e2) -> {
if (e1[0] != e2[0]) {
return e1[0] - e2[0];
} else {
return e2[1] - e1[1];
}
});
List<Integer> f = new ArrayList<>();
f.add(envelopes[0][1]);
for (int i = 1; i < n; ++i) {
int num = envelopes[i][1];
// 比最后一堆堆顶元素都大,新建一个堆存放这个数。
if (num > f.get(f.size() - 1)) {
f.add(num);
} else {
int index = binarySearch(f, num);
// 相当于覆盖堆顶的值。
f.set(index, num);
}
}
// 最长上升子序列的长度就是f集合的大小,也就是一共有几堆。
return f.size();
}
// 根据target找到在数组中的索引
// 寻找左侧边界的二分搜索
public int binarySearch(List<Integer> f, int target) {
int left = 0, right = f.size() - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (f.get(mid) < target) {
left = mid + 1;
} else if (f.get(mid) > target) {
right = mid - 1;
} else if (f.get(mid) == target) {
right = mid - 1;
}
}
return left;
}
}
435. 无重叠区间🍓
给定一个区间的集合 intervals ,其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互不重叠 。
这个题用动态规划也会超时了。
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
Arrays.sort(intervals, (a, b) -> {
return a[0] - b[0];
});
int n = intervals.length;
int[] dp = new int[n];
Arrays.fill(dp, 1);
int res = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < i; j++) {
// 当前区间的左端点大于等于之前区间的右断点就行。
if (intervals[i][0] >= intervals[j][1]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
res = Math.max(res, dp[i]);
}
return n - res;
}
}
贪心解法:
1、从区间集合 intvs 中选择一个区间 x,这个 x 是在当前所有区间中结束最早的(end 最小)。
2、把所有与 x 区间相交的区间从区间集合 intvs 中删除。
3、重复步骤 1 和 2,直到 intvs 为空为止。之前选出的那些 x 就是最大不相交子集。
把这个思路实现成算法的话,可以按每个区间的 end 数值升序排序,因为这样处理之后实现步骤 1 和步骤 2 都方便很多,如下 GIF 所示:
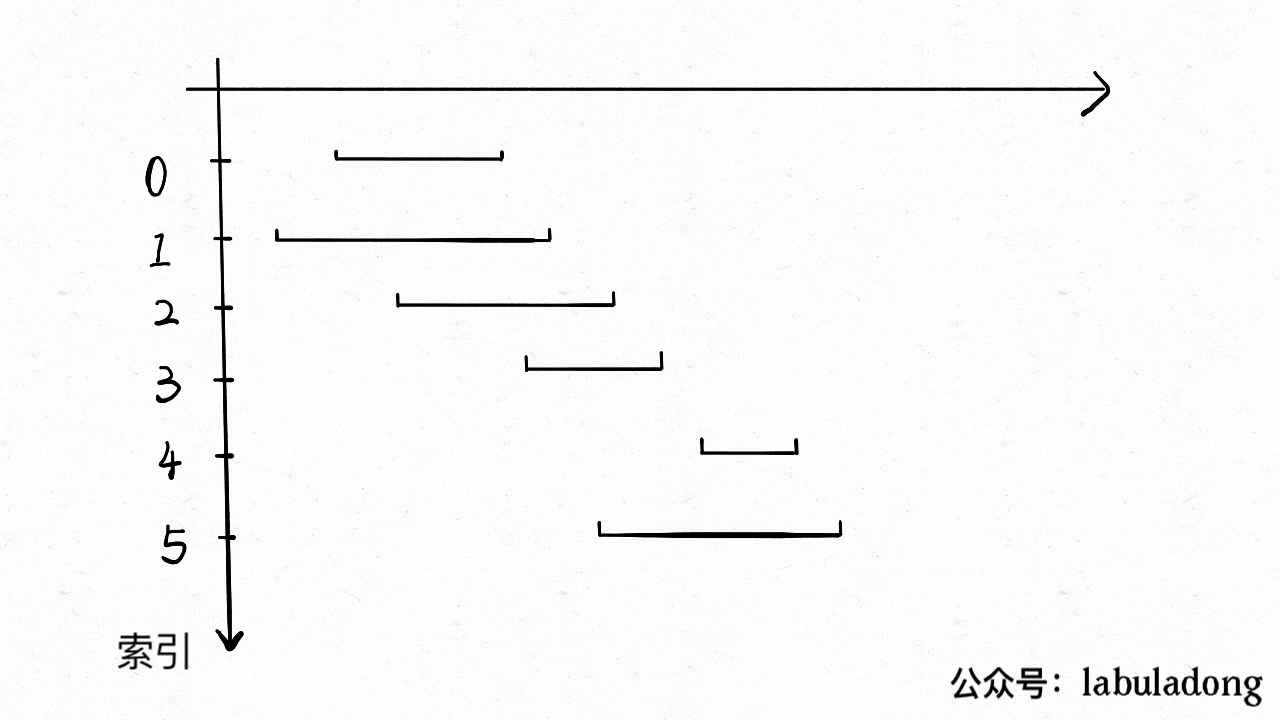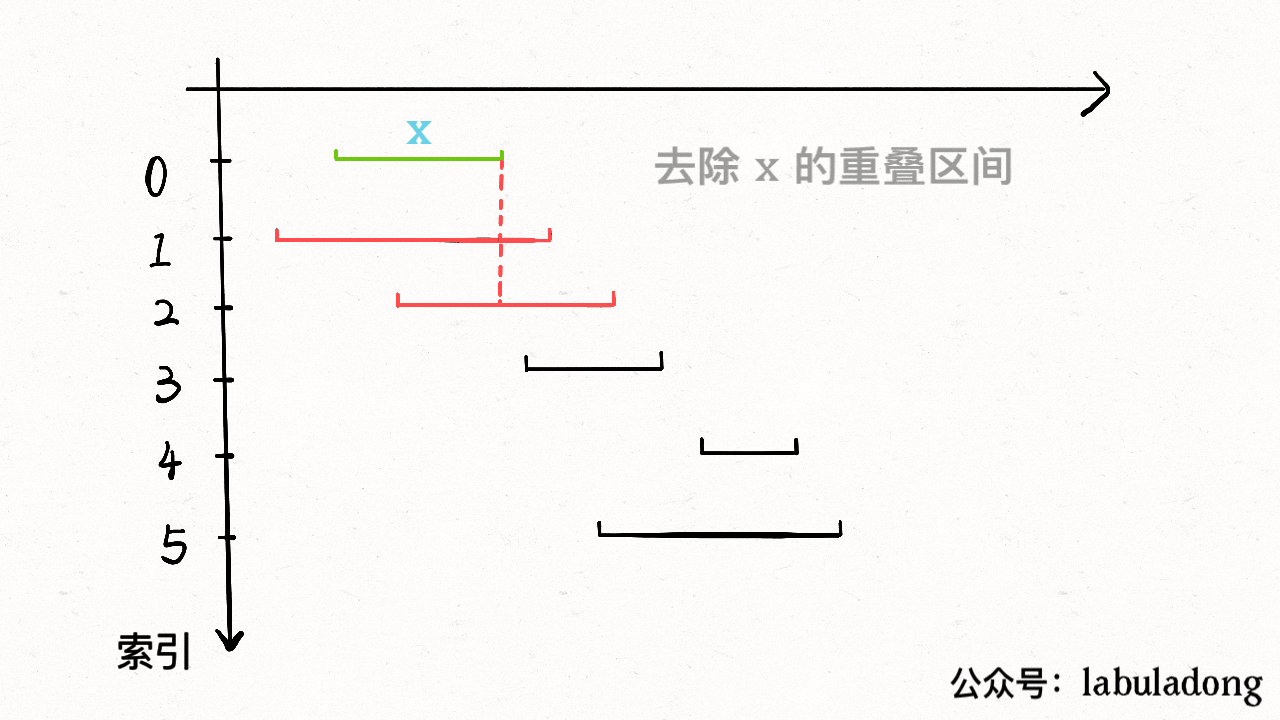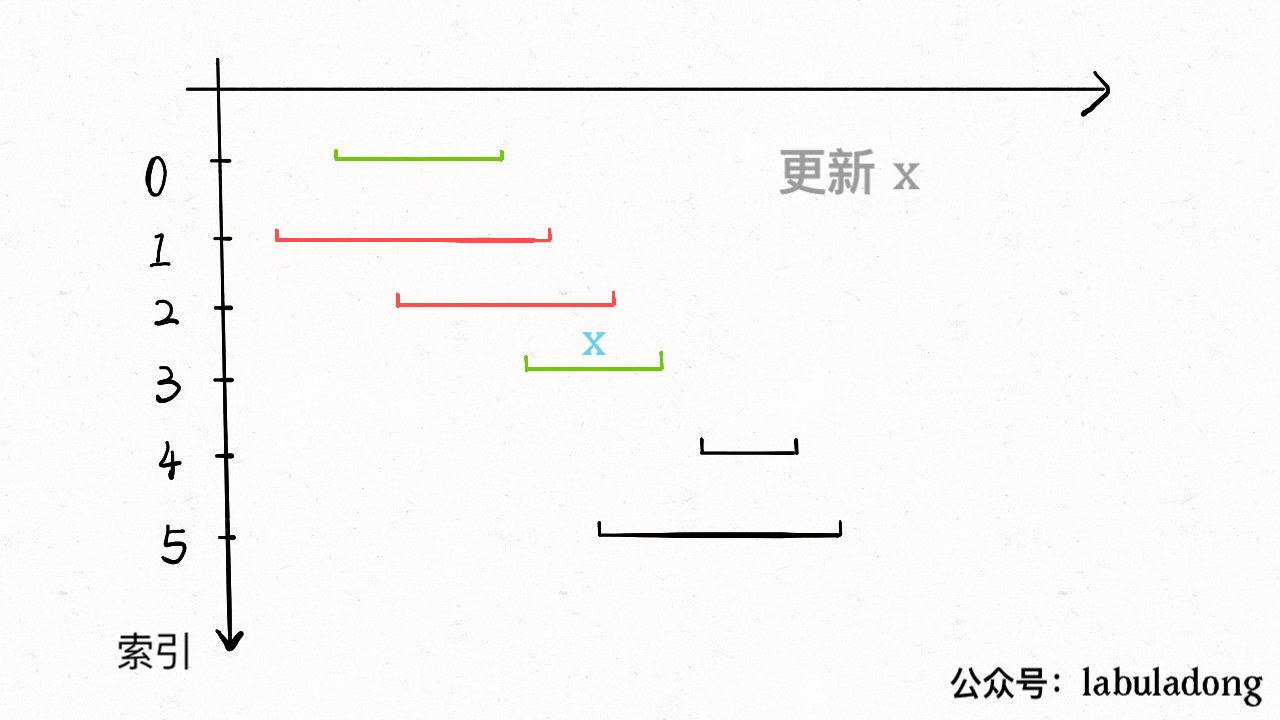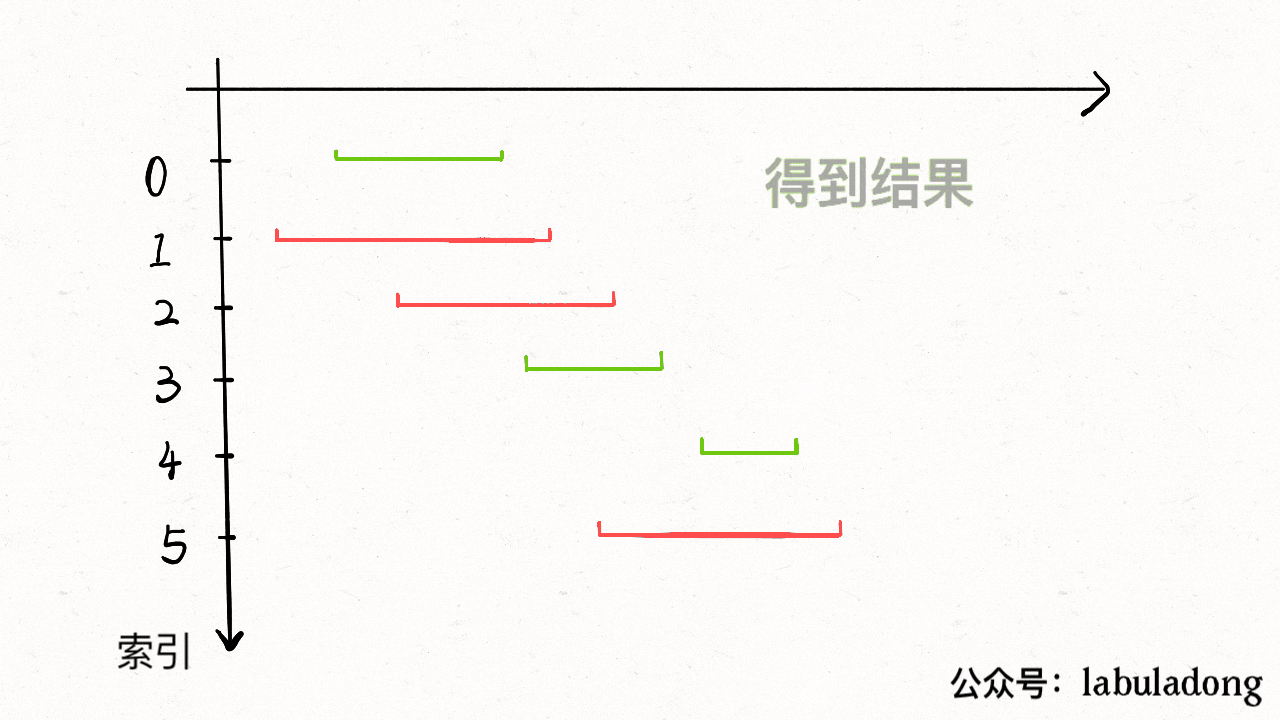
现在来实现算法,对于步骤 1,由于我们预先按照 end 排了序,所以选择 x 是很容易的。关键在于,如何去除与 x 相交的区间,选择下一轮循环的 x 呢?
由于我们事先排了序,不难发现所有与 x 相交的区间必然会与 x 的 end 相交;
如果一个区间不想与 x 的 end 相交,它的 start 必须要大于(或等于)x 的 end:
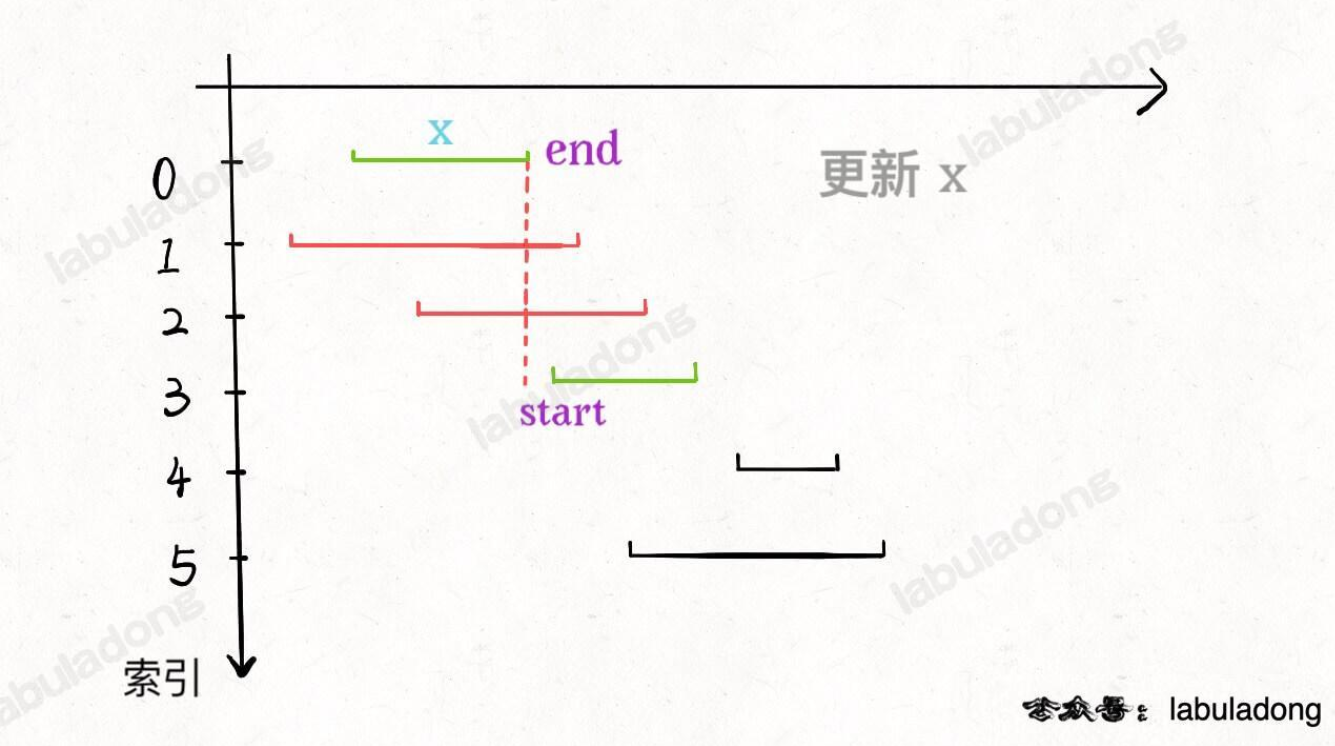
看下代码:
public int intervalSchedule(int[][] intvs) {
if (intvs.length == 0) return 0;
// 按 end 升序排序
Arrays.sort(intvs, new Comparator<int[]>() {
public int compare(int[] a, int[] b) {
return a[1] - b[1];
}
});
// 至少有一个区间不相交
int count = 1;
// 排序后,第一个区间就是 x
int x_end = intvs[0][1];
for (int[] interval : intvs) {
int start = interval[0];
if (start >= x_end) {
// 找到下一个选择的区间了
count++;
x_end = interval[1];
}
}
return count;
}
最终解法:
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
return intervals.length - intervalSchedule(intervals);
}
private int intervalSchedule(int[][] intervals) {
// 按照区间的右端点进行排序。
Arrays.sort(intervals, (a, b) -> {
return a[1] - b[1];
});
int end = intervals[0][1];
int count = 1;
for (int[] interval : intervals) {
int start = interval[0];
if (start >= end) {
count++;
end = interval[1];
}
}
return count;
}
}
646. 最长数对链🍓
给出 n 个数对。 在每一个数对中,第一个数字总是比第二个数字小。
现在,我们定义一种跟随关系,当且仅当 b < c 时,数对(c, d) 才可以跟在 (a, b) 后面。我们用这种形式来构造一个数对链。
给定一个数对集合,找出能够形成的最长数对链的长度。你不需要用到所有的数对,你可以以任何顺序选择其中的一些数对来构造。
class Solution {
public int findLongestChain(int[][] pairs) {
Arrays.sort(pairs, (a, b) -> {
return a[0] - b[0];
});
int n = pairs.length;
int[] dp = new int[n];
Arrays.fill(dp, 1);
int res = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < i; j++) {
if (pairs[i][0] > pairs[j][1]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
res = Math.max(res, dp[i]);
}
return res;
}
}
面试题 08.13. 堆箱子🍓
堆箱子。给你一堆n个箱子,箱子宽 wi、深 di、高 hi。箱子不能翻转,将箱子堆起来时,下面箱子的宽度、高度和深度必须大于上面的箱子。
实现一种方法,搭出最高的一堆箱子。箱堆的高度为每个箱子高度的总和。
输入使用数组[wi, di, hi]表示每个箱子。
673. 最长递增子序列的个数⭐⭐⭐⭐⭐😭
给定一个未排序的整数数组 nums , 返回最长递增子序列的个数 。
注意 这个数列必须是 严格 递增的。
输入: [1,3,5,4,7]
输出: 2
解释: 有两个最长递增子序列,分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。
我们定义两个数组
dp[i]代表以nums[i]结尾的最长递增子序列的长度;
combination[i]表示以nums[i]结尾的最长递增子序列的组合的个数。
这两个数组全部初始化为1,显然当序列长度为1时,最长递增子序列的长度为1,并且所有最长递增子序列的个数至少为1。
用两层for循环的原因是,外层循环遍历nums数组,求出以nums[i]结尾的最长递增子序列的长度以及个数。
内层循环是判断在nums[i]之前是否有严格小于nums[i]的数nums[j],如果有说明nums[i]可以接在nums[j]的后面组成一个递增子序列。
若要LIS成立,我们只需要考虑nums[i] > nums[j]就可以了,其他情况不考虑。
当dp[j] + 1 > dp[i]说明第一次找到这个组合,直接更新dp[i] = dp[j] + 1,combination[i] = combination[j];
当dp[j] + 1 == dp[i]说明找到了能够组成和之前出现过的序列一样长的新序列。
比如上面的例子1 3 5 4 7,最长递增子序列的长度是4。当扫描到4时发现dp[3] + 1 == dp[4],此时1 3 4 7 就和前面出现过的1 3 5 7序列一样长。
class Solution {
public int findNumberOfLIS(int[] nums) {
int len = nums.length;
int[] dp = new int[len];
int[] combination = new int[len];
Arrays.fill(dp, 1);
Arrays.fill(combination, 1);
int max = 1, res = 0;
for (int i = 0; i < len; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
if (dp[j] + 1 > dp[i]) { // 如果+1长于当前LIS则组合数不变。
dp[i] = dp[j] + 1;
combination[i] = combination[j];
} else if (dp[j] + 1 == dp[i]) { // 如果+1等于当前LIS则说明找到了新组合。
combination[i] += combination[j];
}
}
}
max = Math.max(max, dp[i]);
}
// 当nums数组中的数全是相同的,或者全是降序的,
for (int i = 0; i < nums.length; i++) {
if (dp[i] == max) {
res += combination[i];
}
}
return res;
}
}
674. 最长连续递增序列的长度
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1],
nums[r]] 就是连续递增子序列。
输入:nums = [1,3,5,4,7]
输出:3
解释:最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
这题其实和最长递增子序列差不多,只不过这一题要求连续。
class Solution {
public int findLengthOfLCIS(int[] nums) {
int len = nums.length;
int max = 1;
int[] dp = new int[len];
Arrays.fill(dp, 1);
for (int i = 1; i < len; i++) {
if (nums[i] > nums[i - 1]) {
dp[i] = dp[i - 1] + 1;
}
max = Math.max(max, dp[i]);
}
return max;
}
}
滑动窗口解法:
class Solution {
public int findLengthOfLCIS(int[] nums) {
int n = nums.length;
int left = 0, right = 1;
int len = 1;
while (right < n) {
if (nums[right] > nums[right - 1]) {
right++;
} else {
len = Math.max(len, right - left);
left = right;
right++;
}
}
// 循环结束时,别忘了最后的窗口还需要更新一次len。
len = Math.max(len, right - left);
return len;
}
}
516. 最长回文子序列的长度(遍历顺序)🐱🏍
给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
第一种解法:
转换为最长公共子序列的长度。
class Solution {
public int longestPalindromeSubseq(String s) {
// 先反转字符串s
String str = new StringBuilder(s).reverse().toString();
int len1 = s.length(), len2 = len1;
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (s.charAt(i - 1) == str.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[len1][len2];
}
}
子序列问题是常见的算法问题,而且并不好解决。
首先,子序列问题本身就相对子串、子数组更困难一些,因为前者是不连续的序列,而后两者是连续的,就算穷举你都不一定会,更别说求解相关的算法问题了。
一般来说,这类问题都是让你求一个最长子序列,因为最短子序列就是一个字符嘛,没啥可问的。
一旦涉及到子序列和最值,那几乎可以肯定,考察的是动态规划技巧,时间复杂度一般都是 O(n^2)。
区间dp
定义状态:
dp[i] [j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i] [j]。
状态转移:
如果我们想求 dp[i] [j],假设你知道了子问题 dp[i+1] [j-1] 的结果(s[i+1..j-1] 中最长回文子序列的长度)。
你是否能想办法算出 dp[i] [j] 的值(s[i..j] 中,最长回文子序列的长度)呢?
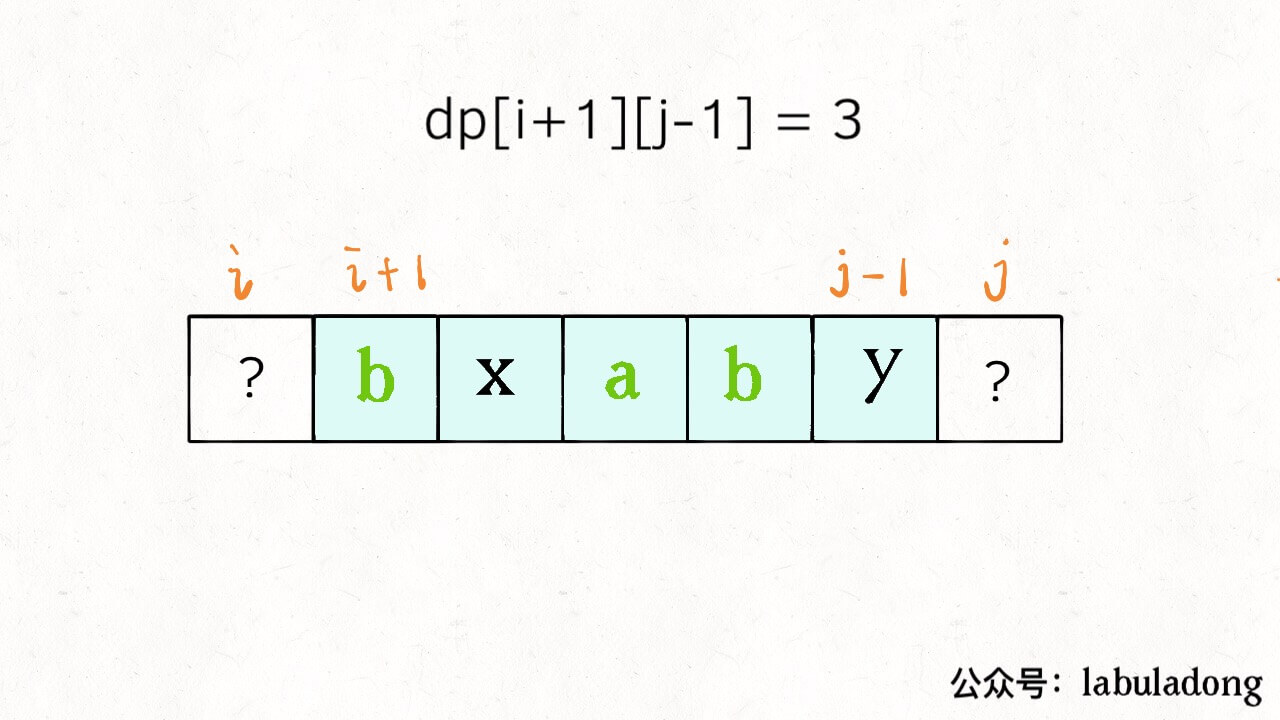
如果它俩相等,那么它俩加上 s[i+1..j-1] 中的最长回文子序列就是 s[i..j] 的最长回文子序列:
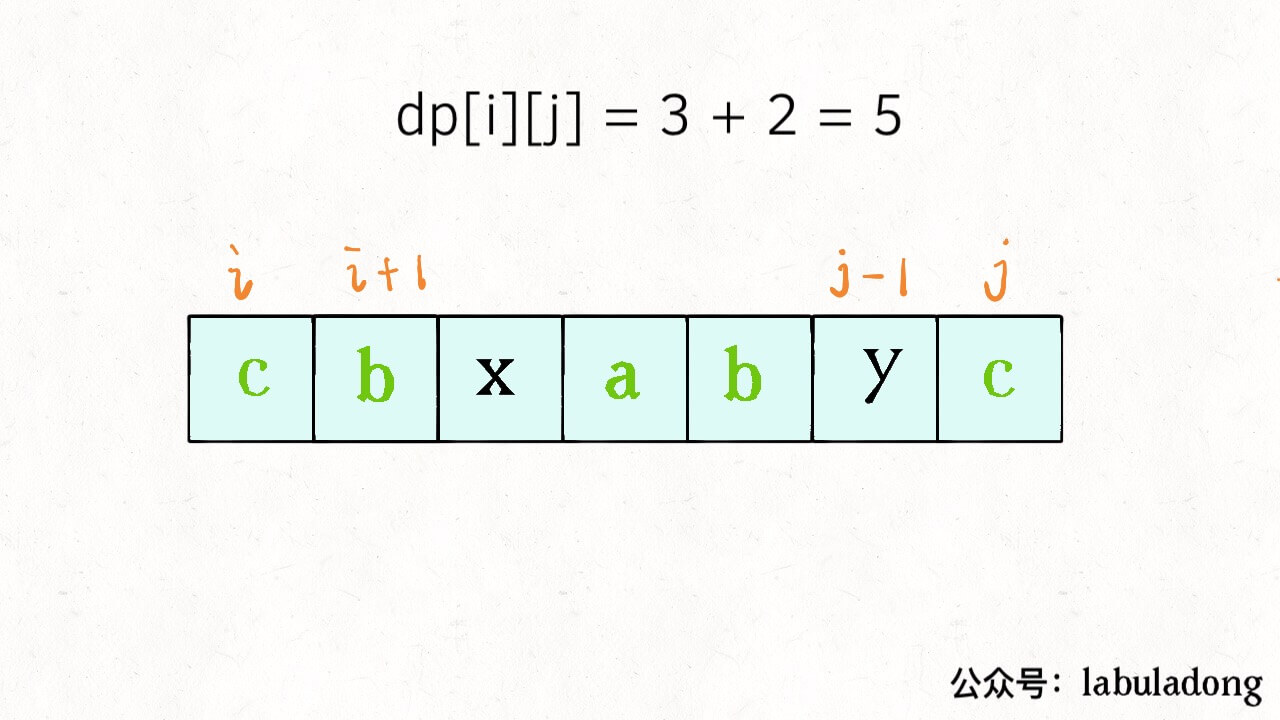
如果它俩不相等,说明它俩不可能同时出现在 s[i..j] 的最长回文子序列中,那么把它俩分别加入 s[i+1..j-1] 中,看看哪个子串产生的回文子序列更长即可:
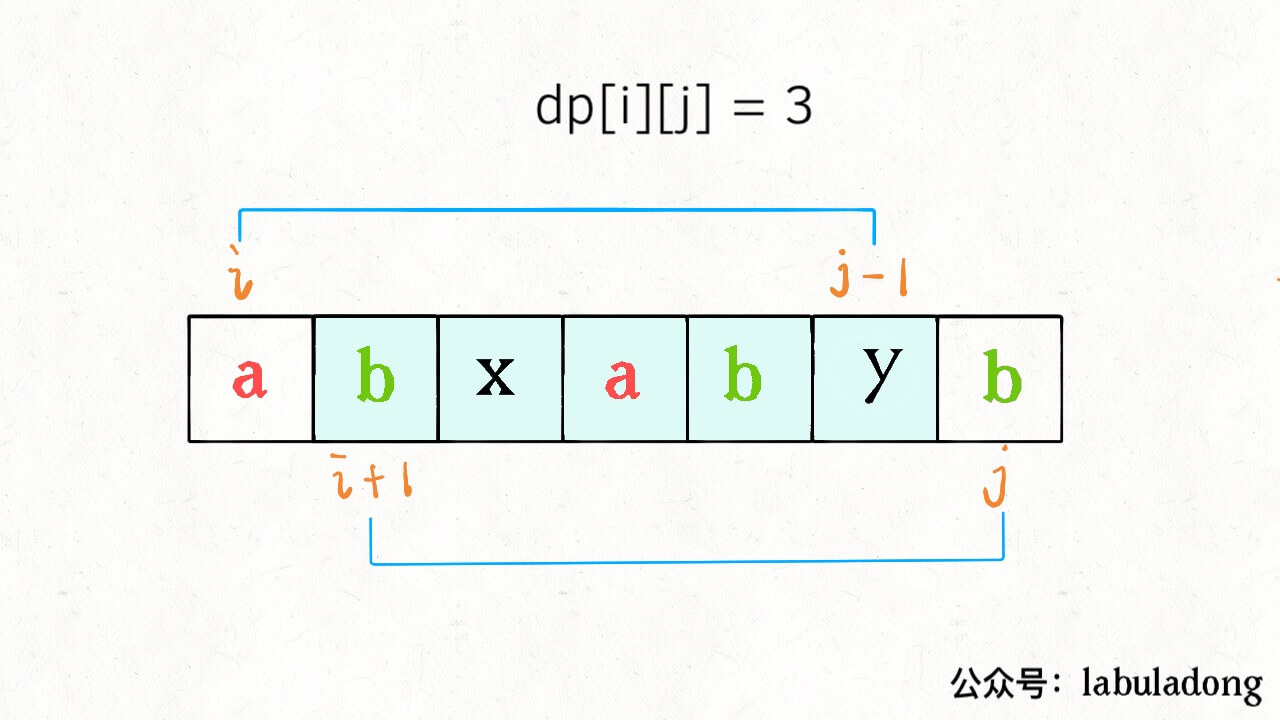
以上两种情况写成代码就是这样:
if (s[i] == s[j]) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}
初始化:
如果只有一个字符,显然最长回文子序列长度是 1,也就是 dp[i] [j] = 1 (i == j)。
因为 i 肯定小于等于 j,所以对于那些 i > j 的位置,根本不存在什么子序列,应该初始化为 0。
另外,看看刚才写的状态转移方程,想求 dp[i] [j] 需要知道 dp[i+1] [j-1],dp[i+1] [j],dp[i] [j-1] 这三个位置,可能会用到左下方,下方,左方的数据来更新。
再看看我们确定的 base case。填入 dp 数组之后是这样:
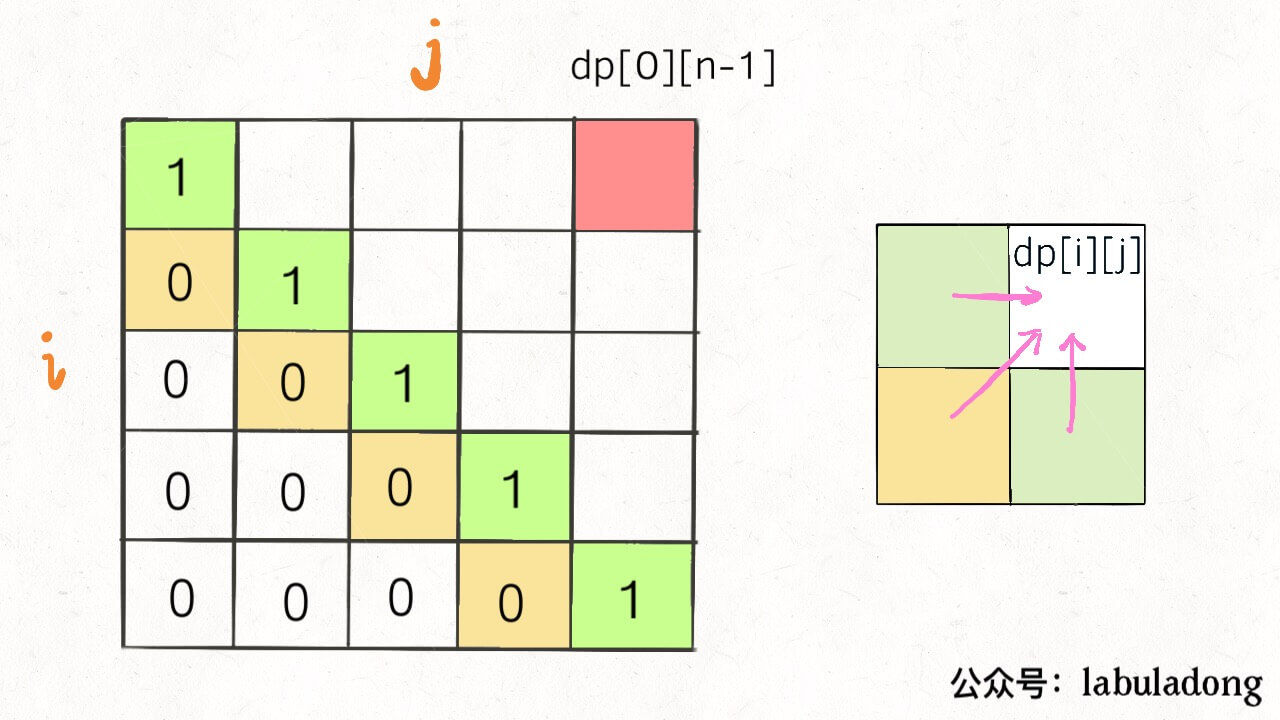
为了保证每次计算 dp[i] [j],左下右方向的位置已经被计算出来,只能斜着遍历或者反着遍历:
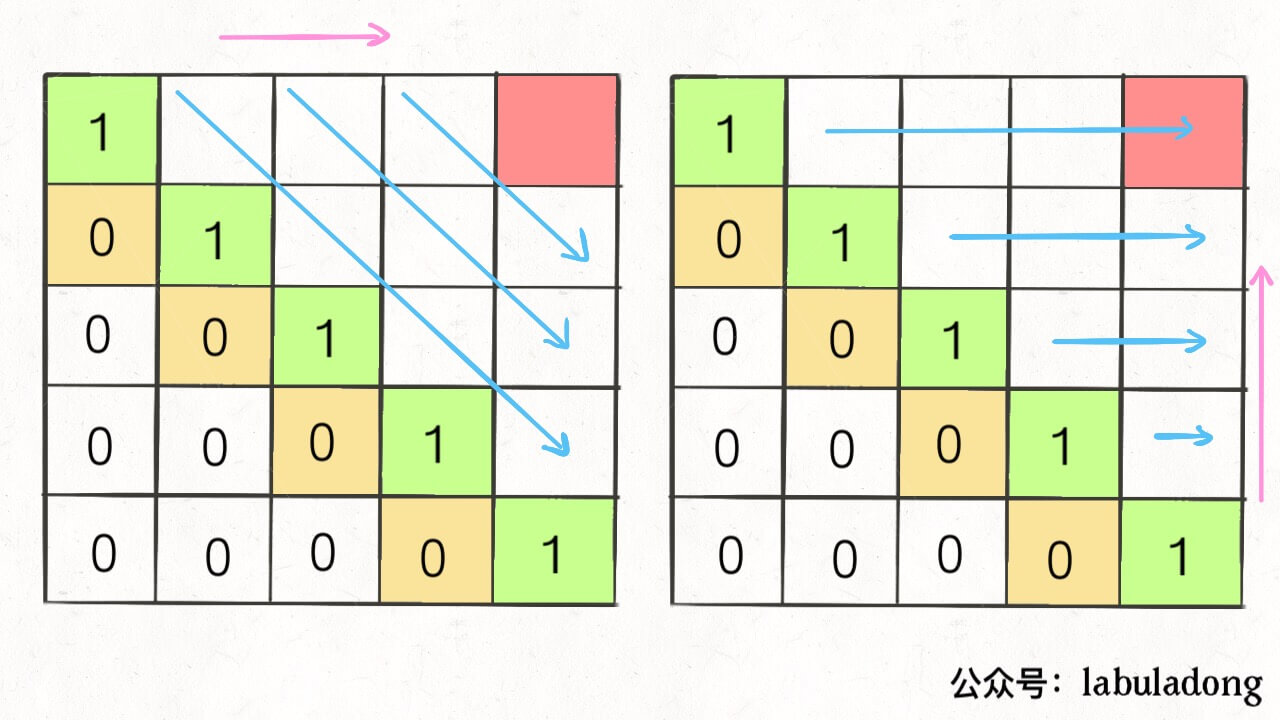
我们选择反着遍历,从上到下,从左到右的遍历。
class Solution {
public int longestPalindromeSubseq(String s) {
int len = s.length();
// 这题和647一样属于区间dp类型
// dp[i][j]代表s在[i, j]范围内最长回文子序列的长度。
int[][] dp = new int[len][len];
// base case 初始化。
// 只有一个字符,最长回文子序列就是1。
for (int i = 0; i < len; i++) {
dp[i][i] = 1;
}
// 这个题是很典型的根据状态转移方程确定遍历顺序。
// 我们看状态转移方程,发现 dp[i][j] 可能由矩阵中左下位置更新而来。
// 也可能由左方和下方的状态更新而来。
// 也就是说这些位置我们要先求出来。
// 遍历顺序就是从下到上,从左到右。
for (int i = len - 1; i >= 0; i--) {
for (int j = i + 1; j < len; j++) {
if (s.charAt(i) == s.charAt(j)) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = Math.max(dp[i][j - 1], dp[i + 1][j]);
}
}
}
// 最终返回代表整个字符串的区间的子序列的长度。
return dp[0][len - 1];
}
}
647. 回文子串的个数(遍历顺序)🐱🏍
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
class Solution {
public int countSubstrings(String s) {
int n = s.length(), ans = 0;
// dp[i][j]:s字符串下标i到下标j的字串是否是一个回文串,即s[i, j]。
boolean[][] dp = new boolean[n][n];
// 这里注意遍历的顺序。
for (int j = 0; j < n; j++) {
for (int i = 0; i <= j; i++) {
// 当两端字母一样时,才可以两端收缩进一步判断。
if (s.charAt(i) == s.charAt(j)) {
// i++,j--,即两端收缩之后i,j指针指向同一个字符或者i超过j了,必然是一个回文串。
if (j - i <= 2) {
dp[i][j] = true;
} else {
// 否则通过收缩之后的子串判断。根据左下方进行更新。
dp[i][j] = dp[i + 1][j - 1];
}
}
}
}
// 因为dp数组记录了某一个区间是不是回文串。
// 遍历每一个子串,统计回文串个数。
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (dp[i][j]) {
ans++;
}
}
}
return ans;
}
}
1312. 让字符串成为回文串的最少插入次数🐱🏍
给你一个字符串 s ,每一次操作你都可以在字符串的任意位置插入任意字符。
请你返回让 s 成为回文串的 最少操作次数 。
「回文串」是正读和反读都相同的字符串。
解题思路:其实这道题可以借助516题最长回文子序列来做,求出字符串中最长的回文子序列之后,字符串中剩下的字符就是需要进行回文配对的。
class Solution {
public int minInsertions(String s) {
int n = s.length();
int res = longestPalindromeSubseq(s);
return n - res;
}
private int longestPalindromeSubseq(String s) {
int n = s.length();
int[][] dp = new int[n][n];
for (int i = 0; i < n; i++) {
dp[i][i] = 1;
}
for (int i = n - 1; i >= 0; i--) {
for (int j = i + 1; j < n; j++) {
if (s.charAt(i) == s.charAt(j)) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
return dp[0][n - 1];
}
}
对字符串 s[i..j],最少需要进行 dp[i][j] 次插入才能变成回文串。
根据 dp 数组的定义,base case 就是 dp[i][i] = 0,因为单个字符本身就是回文串,不需要插入。
然后使用数学归纳法,假设已经计算出了子问题 dp[i+1][j-1] 的值了,思考如何推出 dp[i][j] 的值:
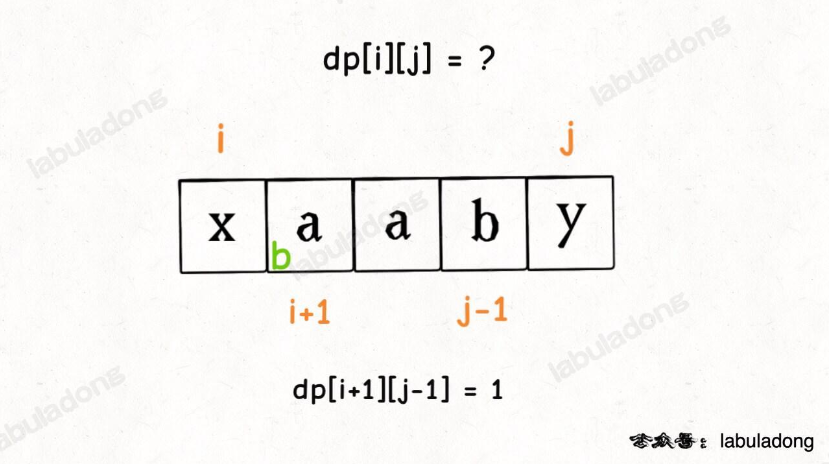
实际上和最长回文子序列问题的状态转移方程非常类似,这里也分两种情况:
if (s[i] == s[j]) {
// 不需要插入任何字符
dp[i][j] = dp[i + 1][j - 1];
} else {
// 把 s[i+1..j] 和 s[i..j-1] 变成回文串,选插入次数较少的
// 然后还要再插入一个 s[i] 或 s[j],使 s[i..j] 配成回文串
dp[i][j] = min(dp[i + 1][j], dp[i][j - 1]) + 1;
}
最后,我们依然采取倒着遍历 dp 数组的方式,写出代码:
class Solution {
public int minInsertions(String s) {
int n = s.length();
// 对字符串 s[i..j],最少需要进行 dp[i][j] 次插入才能变成回文串。
int[][] dp = new int[n][n];
// 注意遍历顺序,从上到下,从左到右,确保状态更新时,其余状态已经知道了。
for (int i = n - 1; i >= 0; i--) {
for (int j = i + 1; j < n; j++) {
// 不需要插入任何字符都是回文。
if (s.charAt(i) == s.charAt(j)) {
dp[i][j] = dp[i + 1][j - 1];
} else {
// 任何一个回文字符串,插入一个字符仍然是回文,比如a b b a在中间插入一个字符仍然是回文。
// 又或者aba在中间插入一个b也仍然是回文。
dp[i][j] = Math.min(dp[i + 1][j], dp[i][j - 1]) + 1;
}
}
}
return dp[0][n - 1];
}
}
718. 最长重复子数组
给两个整数数组 nums1 和 nums2 ,返回两个数组中公共的 、长度最长的子数组的长度。
输入:nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出:3
解释:长度最长的公共子数组是 [3,2,1] 。
子数组是连续的呢。
class Solution {
public int findLength(int[] nums1, int[] nums2) {
int n1 = nums1.length, n2 = nums2.length;
int[][] dp = new int[n1 + 1][n2 + 1];
int res = 0;
// dp[i][j]代表索引从0~i-1和索引0~j-1构成的两个数组中公共的、长度最长的子数组的长度。
// 比如dp[1][1]就代表nums1[0]和nums2[0]这两个数组公共的、长度最长的子树组的长度。
for (int i = 1; i <= n1; i++) {
for (int j = 1; j <= n2; j++) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
res = Math.max(res, dp[i][j]);
}
}
}
return res;
}
}
1143. 最长公共子序列的长度🌈🤩
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。如果不存在公共子序列 ,返回 0 。
一个字符串的子序列是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
解题思路:
求两个数组或者字符串的最长公共子序列问题,肯定是要用动态规划的。下面的题解并不难,你肯定能看懂。
首先,区分两个概念:
子序列可以是不连续的;
子数组(子字符串)需要是连续的。
另外,动态规划也是有套路的:单个数组或者字符串要用动态规划时,可以把动态规划 dp[i] 定义为 nums[0:i] 中想要求的结果;
当两个数组或者字符串要用动态规划时,可以把动态规划定义成两维的 dp[i] [j] ,其含义是在 A[0 : i - 1] 与 B[0 : j - 1] 之间匹配得到的想要的结果。
状态定义:
先给出 dp[][] 数组的定义:dp[i] [j] 表示子串 s1[0..i - 1] 和 s2[0..j - 1] 最长公共子序列的长度。
那么「状态转移方程」是什么呢?
如果 s1[i] = s2[j],dp[i] [j] = dp[i - 1] [j - 1] + 1;
如果 s1[i] != s2[j],dp[i] [j] = Math.max(dp[i] [j - 1], dp[i - 1] [j])。
那么「base case」是什么呢?只要两个字符串有一个是空字符串,显然最长公共子序列长度为0。
如上图粉色标记出来的就是 base case。橙色标记出来的是相等的情况,其余是不等的情况
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int n1 = text1.length(), n2 = text2.length();
int[][] dp = new int[n1 + 1][n2 + 1];
// dp[i][j]表示text1 索引下标0-索引下标i - 1的子串和 text2索引下标0-索引下标j - 1的子串 的最长公共子序列长度。
// dp[0][0]表示两个空字符串的最长公共子序列长度
// dp[0][j]表示text1空字符串和text2的最长公共子序列长度
// dp[i][0]表示text1和空字符串text2的最长公共子序列长度
for (int i = 1; i <= n1; i++) {
for (int j = 1; j <= n2; j++) {
if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[n1][n2];
}
}
392. 判断子序列🌈🤩
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。
例如,"ace"是"abcde"的一个子序列,而"aec"不是。
状态定义:
dp[i] [j]代表s以下标i - 1结尾的子串和t以下标j - 1结尾的子串相同子序列的长度。
状态转移:
当s.charAt(i - 1) == t.charAt(j - 1)时,dp[i] [j] = dp[i - 1] [j - 1] + 1;
当s.charAt(i - 1) != t.charAt(j- 1)时,dp[i] [j] = dp[i] [j - 1]。
初始化:
从递推公式可以看出dp[i] [j]都是依赖于dp[i - 1] [j - 1] 和 dp[i] [j - 1],所以dp[0] [0]和dp[i] [0]是一定要初始化的。
这里大家已经可以发现,在定义dp[i] [j]含义的时候为什么要表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i] [j]。
因为这样的定义在dp二维矩阵中可以留出初始化的区间,如图:

class Solution {
public boolean isSubsequence(String s, String t) {
int len1 = s.length();
int len2 = t.length();
// 开辟dp数组时注意长度,因为dp数组的0行0列都是base case,需要多1列1行
// 才能存储下所有的情况。
int[][] dp = new int[len1 + 1][len2 + 1];
// len1更短
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (s.charAt(i - 1) == t.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = dp[i][j - 1]; // 这里不考虑dp[i - 1][j]的原因是我们知道s是更短的字符串。
}
}
}
if (dp[len1][len2] == len1) {
return true;
} else {
return false;
}
}
}
关于这道题为什么不像1143题那样用 dp[i] [j] = Math.max(dp[i - 1] [j], dp[i] [j - 1])。因为这题我们知道s是长度更短的,并且遍历s的字符在外循环。举个例子:
s = afe,t = aecde。当遍历到s字符串的e字符,t字符串的c字符时。两个字符不相等,afe和aec的最长公共子序列与afe和ae的最长公共子序列相等。此时没问题
但是当s = aecde,t = afe时。当遍历到s字符串的c字符,t字符串的e字符时。两个字符不相等,如果还是j退后一步。此时就会出错,在这个时候是aec和af的最长
公共子序列作为aec和afe的最长公共子序列。明显不对。分析其根本原因是,不能够让较短的字符串往后退一步。这样有可能出错。
1143题就是不知道两个字符串的长度,所有才会取都往后退一步的最大值。
1035. 不相交的线🌈🤩
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足满足:
- nums1[i] == nums2[j];
- 且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
本题说是求绘制的最大连线数,其实就是求两个字符串的最长公共子序列的长度!
class Solution {
public int maxUncrossedLines(int[] nums1, int[] nums2) {
int n1 = nums1.length, n2 = nums2.length;
int[][] dp = new int[n1 + 1][n2 + 1];
for (int i = 1; i <= n1; i++) {
for (int j = 1; j<= n2; j++) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[n1][n2];
}
}
115. 字符串s中子序列t出现的个数🤩
给定一个字符串 s 和一个字符串 t ,计算在 s 的子序列中 t 出现的个数。
字符串的一个 子序列 是指,通过删除一些(也可以不删除)字符且不干扰剩余字符相对位置所组成的新字符串。
(例如,"ACE" 是 "ABCDE" 的一个子序列,而 "AEC" 不是)
题目数据保证答案符合 32 位带符号整数范围。
1、确定dp数组以及下标的含义
这道题的关键在于 dp 数组状态的定义,当 i 和 j 都大于等于 1 时,我们定义dp [i] [j] 为字符串s中以索引 i - 1 处的字符结尾的子字符串的子序列(字符串s的前 i 个
字符组成的子序列)中包含字符串 t 中以索引 j - 1结尾的子字符串(字符串 t 的前 i 个字符组成的字符串) 的个数。
2、确定递推公式
这一类问题,基本是要分析两种情况。
- s[i - 1] 与 t[j - 1]相等;
- s[i - 1] 与 t[j - 1] 不相等。
当s[i - 1] 与 t[j - 1] 相等时,dp[i] [j]可以有两部分组成。
一部分是用 s[i - 1] 来匹配,那么个数为 dp[i - 1] [j - 1],因为dp数组代表子序列出现的个数,当s[i - 1] == t[j - 1]时增加一个字符子序列出现的次数和不增加相同。
一部分是不用 s[i - 1] 来匹配,个数为 dp[i - 1] [j],j肯定是不能往后移动的,因为我们要将j匹配到最后t.len。
这里可能有同学不明白了,为什么还要考虑不用s[i - 1]来匹配,都相同了指定要匹配啊。
例如: s:bagg 和 t:bag ,s[3] 和 t[2]是相同的,但是字符串s也可以不用s[3]来匹配,即用s[0]s[1]s[2]组成的bag。
当然也可以用s[3]来匹配,即:s[0]s[1]s[3]组成的bag。
所以当s[i - 1] 与 t[j - 1]相等时,dp[i] [j] = dp[i - 1] [j - 1] + dp[i - 1] [j];
当s[i - 1] 与 t[j - 1]不相等时,dp[i] [j]只有一部分组成,不用s[i - 1]来匹配,即:dp[i - 1] [j]
所以递推公式为:dp[i] [j] = dp[i - 1] [j];这里为什么是dp[i- 1] [j]因为s字符串更长。
3、dp数组如何初始化
从递推公式 dp[i] [j] = dp[i - 1] [j - 1] + dp[i - 1] [j] 和 dp[i] [j] = dp[i - 1] [j] 中可以看出 dp[i] [0] 和 dp[0] [j] 是一定要初始化的。
每次当初始化的时候,都要回顾一下 dp[i] [j] 的定义,不要凭感觉初始化。当 i 和 j 等于0 时分别代表字符串s和字符串t是空字符串。
值得注意的是dp数组不再是统一的含义,当i和j都大于1时又是另一种含义。
dp[i] [0] 表示什么呢?
dp[i] [0] 表示:以i-1为结尾的s可以随便删除元素,出现空字符串的个数。
那么 dp[i] [0] 一定都是1,因为也就是把以i-1为结尾的s,删除所有元素,出现空字符串的个数就是1。
再来看 dp[0] [j],dp[0] [j]:空字符串s可以随便删除元素,出现以j-1为结尾的字符串t的个数。
那么 dp[0] [j] 一定都是0,s如论如何也变成不了t。
最后就要看一个特殊位置了,即:dp[0] [0] 应该是多少。
dp[0] [0] 应该是1,空字符串s,可以删除0个元素,变成空字符串t。
注意:经过写代码验证这题的用例s的长度总是大于等于t的长度的。
class Solution {
public int numDistinct(String s, String t) {
// sLength和tLength分别是两个字符串的长度
int sLen = s.length();
int tLen = t.length();
// 因为我们用dp数组的i和j表示的是字符串s的i - 1和字符串t的j - 1索引下标的状态。
// 所以dp数组的两个维度的长度都要加1。
// dp[i][j]表示以下标i-1结尾的s的子序列中以j-1结尾的t的子字符串出现的个数。
// dp[i][j]表示s的前j个字符构成的字符串的子序列中出现t的前i个字符构成的字符串的个数。
int[][] dp = new int[sLen + 1][tLen + 1];
// 初始化dp数组
// 字符串t为空是所有字符串的子集
// dp[0][0]代表两个都是空字符串的,空字符串s的子序列中空字符串出现的个数是1。
for (int i = 0; i < sLen + 1; i++) {
dp[i][0] = 1;
}
for (int i = 1; i <= sLen; i++) {
for (int j = 1; j <= tLen; j++) {
if (s.charAt(i - 1) == t.charAt(j - 1)) {
// 当i-1位置和j-1位置字符相等时:
// 可以用s[i - 1]来匹配,那么个数为dp[i - 1][j - 1];
// 不用s[i - 1]来匹配时,个数为dp[i - 1][j]。
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
} else {
// 当i-1位置和j-1位置字符不相等时
// 只能用s中i - 2位置结束的子序列中匹配t中j - 1位置结束的字串。
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[sLen][tLen];
}
}
583. 两个字符串的删除操作🤩
给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。
每步 可以删除任意一个字符串中的一个字符。
输入: word1 = "sea", word2 = "eat"
输出: 2
解释: 第一步将 "sea" 变为 "ea" ,第二步将 "eat "变为 "ea"。
定义状态:
dp[i] [j]表示word1以i - 1下标结尾的字串与word2以j - 1结尾的字串,达到相等时,需要删除元素的最少次数。
状态转移:
- 当word1[i - 1] 与 word2[j - 1]相同的时候;
- 当word1[i - 1] 与 word2[j - 1]不相同的时候。
当word1[i - 1] 与 word2[j - 1]相同的时候,dp[i] [j] = dp[i - 1] [j - 1]。
当word1[i - 1] 与 word2[j - 1]不相同的时候,有三种情况:
情况一:删word1[i - 1],最少操作次数为dp[i - 1] [j] + 1;
情况二:删word2[j - 1],最少操作次数为dp[i] [j - 1] + 1;
情况三:同时删word1[i - 1]和word2[j - 1],操作的最少次数为dp[i - 1] [j - 1] + 2。
那最后当然是取最小值,所以当word1[i - 1] 与 word2[j - 1]不相同的时候,递推公式:dp[i][j] = min({dp[i - 1] [j - 1] + 2, dp[i - 1] [j] + 1, dp[i] [j - 1] + 1});
class Solution {
public int minDistance(String word1, String word2) {
int len1 = word1.length(), len2 = word2.length();
// dp[i][j]表示word1以i - 1下标结尾的字串与word2以j - 1结尾的字串,达到相等时,需要删除元素的最少次数。
int[][] dp = new int[len1 + 1][len2 + 1];
// 初始化
// 当word2是空字符串时,word1需要删除元素的次数。
for (int i = 0; i <= len1; i++) {
dp[i][0] = i;
}
// 当word1是空字符串时,word2需要删除元素的次数。
for (int j = 0; j <= len2; j++) {
dp[0][j] = j;
}
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = Math.min(dp[i - 1][j - 1] + 2, Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1));
}
}
}
return dp[len1][len2];
}
}
另一种做法先求出两个字符串的最长公共子序列的长度,拿两个字符串的长度之和减去2倍的最长公共子序列的长度就可以了。
class Solution {
public int minDistance(String word1, String word2) {
int len1 = word1.length();
int len2 = word2.length();
// dp[i][j]
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return (len1 + len2) - 2 * dp[len1][len2];
}
}
贪心
12. 整数转罗马数字
class Solution {
public String intToRoman(int num) {
int[] nums = {1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1};
String[] romans = {"M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"};
int index = 0;
StringBuilder sb = new StringBuilder();
while (index < 13) {
while (num >= nums[index]) {
sb.append(romans[index]);
num = num - nums[index];
}
if (num == 0) {
break;
}
index++;
}
return sb.toString();
}
}
设计贪心算法如下:每一步都使用当前对应阿拉伯数字较大的罗马数字作为加法因子,最后得到罗马数字表示就是长度最少的。
贪心算法的证明:
我们先说 题目中隐含的条件,这是我在调试的时候发现的:900(CM)、400(CD),90、40、9、4 这些数字只允许出现一次,即:1800
不能对应 CMCM,应该对应 MDCCC,也就是说,如果能拆分 4、9、40、90、400、900 作为加法因子,它们只能出现一次。
剩下的可以出现多次的字符有 1、5、10、50、100、500、1000,它们呈明显的倍数关系。例如 1000 = 500 × 2,能用 1000 就不应该用 2 个 500。贪心选择可
以保证使用的字符在这样的规则下字符最少。
55. 跳跃游戏⭐⭐
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
刚看到本题一开始可能想:当前位置元素如果是3,我究竟是跳一步呢,还是两步呢,还是三步呢,究竟跳几步才是最优呢?
其实跳几步无所谓,关键在于可跳的覆盖范围!
不一定非要明确一次究竟跳几步,每次取最大的跳跃步数,这个就是可以跳跃的覆盖范围。
这个范围内,别管是怎么跳的,反正一定可以跳过来。
那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点!
每次移动取最大跳跃步数(得到最大的覆盖范围),每移动一个单位,就更新最大覆盖范围。
贪心算法局部最优解:每次取最大跳跃步数(取最大覆盖范围),整体最优解:最后得到整体最大覆盖范围,看是否能到终点。

class Solution {
public boolean canJump(int[] nums) {
int n = nums.length;
// 记录当前能跳到的最远位置
int max = 0;
for (int i = 0; i < n; ++i) {
//当前能跳到的最远位置
if (i <= max) {
// 如果当前位置能跳到最远位置,则可以跳到下一个位置
max = Math.max(max, i + nums[i]);
if (max >= n - 1) {
return true;
}
}
}
return false;
}
}
class Solution {
public boolean canJump(int[] nums) {
int len = nums.length;
int max = 0;
for (int i = 0; i <= max; i++) {
max = Math.max(max, i + nums[i]);
if (max >= len - 1) {
return true;
}
}
return false;
}
}
45. 跳跃游戏 II⭐⭐
给你一个非负整数数组 nums ,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
假设你总是可以到达数组的最后一个位置。
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
class Solution {
public int jump(int[] nums) {
int len = nums.length;
if (len == 1) {
return 0;
}
// 表示当前遍历到的数组下标能覆盖到那个下标为止。
int curDistance = 0;
// 表示下一步最大的覆盖下标位置
int maxDistance = 0;
// 记录跳跃的次数
int count = 0;
for (int i = 0; i < len; i++) {
maxDistance = Math.max(maxDistance, i + nums[i]);
// 说明再跳一次就能够到达数组最后一个位置了。
if (maxDistance >= len - 1) {
count++;
break;
}
// 来到了当前覆盖范围的最后一个下标时,更新下一步可达的最大区域。
if (i == curDistance) {
curDistance = maxDistance;
count++;
}
}
return count;
}
}
253. 会议室 II
给你一个会议时间安排的数组 intervals ,每个会议时间都会包括开始和结束的时间 intervals[i] = [starti, endi] ,返回 所需会议室的最小数量 。
示例 1:
输入:intervals = [[0,30],[5,10],[15,20]]
输出:2示例 2:
输入:intervals = [[7,10],[2,4]]
输出:1
406. 根据身高重建队列⭐
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。
每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性
(queue[0] 是排在队列前面的人)。
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释:
编号为 0 的人身高为 5 ,没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ,没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ,有 2 个身高更高或者相同的人排在他前面,即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
编号为 4 的人身高为 4 ,有 4 个身高更高或者相同的人排在他前面,即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。
参考题解:https://programmercarl.com/0406.根据身高重建队列.html#思路
排序的技巧
class Solution {
public int[][] reconstructQueue(int[][] people) {
// 身高从大到小排(身高相同k小的站前面)
Arrays.sort(people, (a, b) -> {
if (a[0] == b[0]) {
return a[1] - b[1];
}
return b[0] - a[0];
});
LinkedList<int[]> que = new LinkedList<>();
for (int[] p : people) {
que.add(p[1], p);
}
return que.toArray(new int[people.length][]);
}
}
452. 用最少数量的箭引爆气球

只是有一点不一样,在 intervalSchedule 算法中,如果两个区间的边界触碰,不算重叠;
而按照这道题目的描述,箭头如果碰到气球的边界气球也会爆炸,所以说相当于区间的边界触碰也算重叠:
class Solution {
// 区间调度问题
public int findMinArrowShots(int[][] intvs) {
if (intvs.length == 0) return 0;
// 按 end 升序排序
Arrays.sort(intvs, new Comparator<int[]>() {
public int compare(int[] a, int[] b) {
return Integer.compare(a[1], b[1]);
}
});
// 至少有一个区间不相交
int count = 1;
// 排序后,第一个区间就是 x
int x_end = intvs[0][1];
for (int[] interval : intvs) {
int start = interval[0];
// 把 >= 改成 > 就行了
if (start > x_end) {
count++;
x_end = interval[1];
}
}
return count;
}
}
455. 分发饼干
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以
将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
用小饼干喂饱小胃口
class Solution {
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int start = 0;
int count = 0;
// 注意for循环执行的条件
// i < s.length && start < g.length
for (int i = 0; i < s.length && start < g.length; i++) {
if (s[i] >= g[start]) {
count++;
start++;
}
}
return count;
}
}
376. 摆动序列⭐
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等
元素的序列也视作摆动序列。
- 例如, [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ,因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
- 相反,[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
给你一个整数数组 nums ,返回 nums 中作为 摆动序列 的 最长子序列的长度 。
动态规划解法:
class Solution {
public int wiggleMaxLength(int[] nums) {
int len = nums.length;
// dp[i][0]表示在索引下标i位置以降序结尾的最长摆动子序列的长度;
// dp[i][1]表示索引下标i位置以升序结尾的最长摆动子序列的长度。
int[][] dp = new int[len][2];
// 初始化,数组第一个元素我们既可以看成是降序结尾,也可以看作是升序结尾。
dp[0][0] = 1;
dp[0][1] = 1;
for (int i = 1; i < len; i++) {
if (nums[i] > nums[i - 1]) {
dp[i][0] = dp[i - 1][0];
dp[i][1] = dp[i - 1][0] + 1;
} else if (nums[i] < nums[i - 1]) {
dp[i][0] = dp[i - 1][1] + 1;
dp[i][1] = dp[i - 1][1];
} else {
dp[i][0] = dp[i - 1][0];
dp[i][1] = dp[i - 1][1];
}
}
return Math.max(dp[len - 1][0], dp[len - 1][1]);
}
}
贪心解法:
class Solution {
public int wiggleMaxLength(int[] nums) {
if (nums.length <= 1) {
return nums.length;
}
// 当前差值
int curDiff = 0;
// 上一个差值
int preDiff = 0;
int count = 1;
for (int i = 1; i < nums.length; i++) {
// 得到当前差值
curDiff = nums[i] - nums[i - 1];
// 如果当前差值和上一个差值为一正一负
// 等于0的情况表示初始时的preDiff
if ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {
count++;
preDiff = curDiff;
}
}
return count;
}
}
621. 任务调度器
给你一个用字符数组 tasks 表示的 CPU 需要执行的任务列表。其中每个字母表示一种不同种类的任务。任务可以以任意顺序执行,并且每个任务都可以在 1 个单
位时间内执行完。在任何一个单位时间,CPU 可以完成一个任务,或者处于待命状态。
然而,两个 相同种类 的任务之间必须有长度为整数 n 的冷却时间,因此至少有连续 n 个单位时间内 CPU 在执行不同的任务,或者在待命状态。
你需要计算完成所有任务所需要的 最短时间 。
参考题解:https://leetcode.cn/problems/task-scheduler/solution/tong-si-xiang-jian-ji-gao-xiao-by-hzhu212/
class Solution {
public int leastInterval(char[] tasks, int n) {
int[] arr = new int[26];
// 记录每种字符出现的次数
for (char c : tasks) {
arr[c - 'A']++;
}
int max = 0;
// 找到字符出现最多的次数
for (int i = 0; i < 26; i++) {
max = Math.max(max, arr[i]);
}
int ret = (max - 1) * (n + 1);
for (int i = 0; i < 26; i++) {
if (arr[i] == max) {
ret++;
}
}
return Math.max(ret, tasks.length);
}
}
860. 柠檬水找零
在柠檬水摊上,每一杯柠檬水的售价为 5 美元。顾客排队购买你的产品,(按账单 bills 支付的顺序)一次购买一杯。
每位顾客只买一杯柠檬水,然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零,也就是说净交易是每位顾客向你支付 5 美元。
注意,一开始你手头没有任何零钱。
给你一个整数数组 bills ,其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零,返回 true ,否则返回 false 。
解题思路:
吊炸天的求解: 由于顾客买柠檬水的面值是固定的:5,10,20;
if(顾客花费== 5) five++;
if(顾客花费== 10) five--; ten++;
if(顾客花费==20) five--; ten--; 或者if(ten < 0) five -= 3;
那么我们如何判定终止条件呢? 我们发现,无论顾客花费多少钱买柠檬水我们要想顺利找零,手中必须要有5美元的零钱;显然,终止条件是判断if(five < 0);
class Solution {
public boolean lemonadeChange(int[] bills) {
int five = 0;
int ten = 0;
for (int bill : bills) {
if (bill == 5) {
five++;
} else if (bill == 10) {
five--;
ten++;
} else if (bill == 20) {
if (ten != 0) {
ten--;
five--;
} else {
five -= 3;
}
}
if (five < 0) {
return false;
}
}
return true;
}
}
1005. K 次取反后最大化的数组和
给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组:
- 选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。
重复这个过程恰好 k 次。可以多次选择同一个下标 i 。
以这种方式修改数组后,返回数组 可能的最大和 。
class Solution {
public int largestSumAfterKNegations(int[] nums, int k) {
Arrays.sort(nums);
for (int i = 0; i < nums.length; i++) {
if (nums[i] < 0) {
nums[i] = -nums[i];
k--;
if (k == 0) {
break;
}
}
}
if (k != 0) {
Arrays.sort(nums);
for (int i = 0; i < nums.length; i++) {
int count = k;
for (int j = 0; j < count; j++) {
k--;
nums[i] = -nums[i];
}
if (k == 0) {
break;
}
}
}
int sum = 0;
for (int num : nums) {
sum += num;
}
return sum;
}
}
134. 加油站⭐
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
解题思路:
首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈,说明 各个站点的加油站 剩油量rest[i]相加一定是大于等于零的。
每个加油站的剩余量 rest[i] 为 gas[i] - cost[i]。
i从0开始累加rest[i],和记为curSum,一旦curSum小于零,说明[0, i]区间都不能作为起始位置,起始位置从i+1算起,再从0计算curSum。
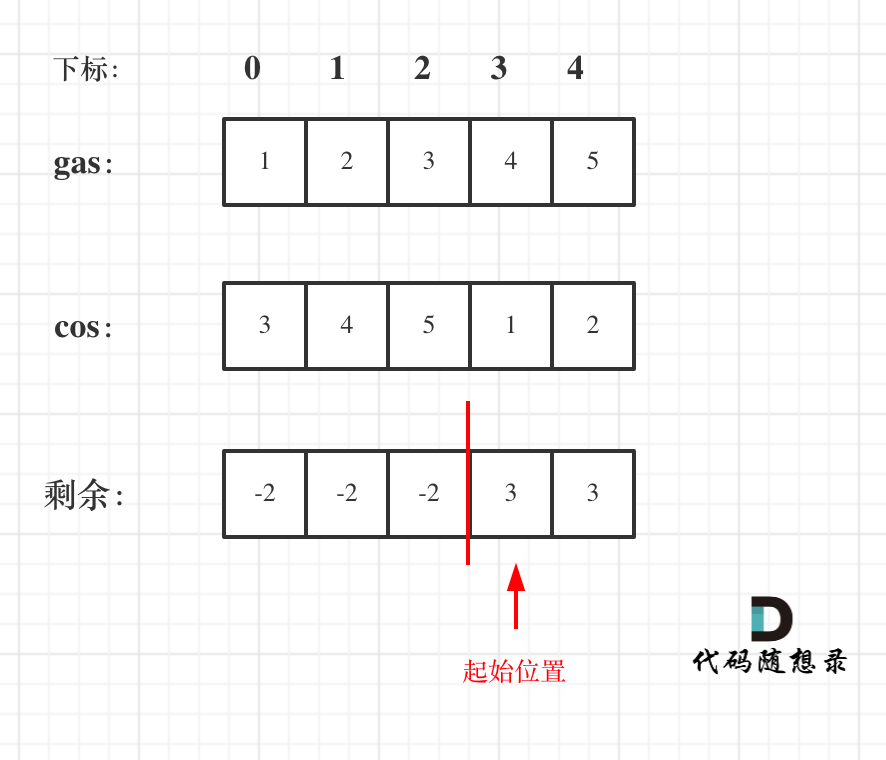
那么为什么一旦[i,j] 区间和为负数,起始位置就可以是j+1呢,j+1后面就不会出现更大的负数?
如果出现更大的负数,就是更新j,那么起始位置又变成新的j+1了。
而且j之前出现了多少负数,j后面就会出现多少正数,因为耗油总和是大于零的(前提我们已经确定了一定可以跑完全程)。
那么局部最优:当前累加rest[j]的和curSum一旦小于0,起始位置至少要是j+1,因为从j开始一定不行。全局最优:找到可以跑一圈的起始位置。
局部最优可以推出全局最优,找不出反例,试试贪心!
class Solution {
public int canCompleteCircuit(int[] gas, int[] cost) {
int curSum = 0;
int totalSum = 0;
int index = 0;
for (int i = 0; i < gas.length; i++) {
curSum += gas[i] - cost[i];
totalSum += gas[i] - cost[i];
if (curSum < 0) {
index = i + 1;
curSum = 0;
}
}
if (totalSum < 0) {
return -1;
}
return index;
}
}
135. 分发糖果⭐
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。
你需要按照以下要求,给这些孩子分发糖果:
- 每个孩子至少分配到 1 个糖果。
- 相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果,计算并返回需要准备的 最少糖果数目 。
参考题解:
https://leetcode.cn/problems/candy/solution/candy-cong-zuo-zhi-you-cong-you-zhi-zuo-qu-zui-da-/
https://programmercarl.com/0135.分发糖果.html#思路
这道题目一定是要确定一边之后,再确定另一边,例如比较每一个孩子的左边,然后再比较右边,如果两边一起考虑一定会顾此失彼。
先确定右边评分大于左边的情况(也就是从前向后遍历)
此时局部最优:只要右边评分比左边大,右边的孩子就多一个糖果,全局最优:相邻的孩子中,评分高的右孩子获得比左边孩子更多的糖果。
class Solution {
public int candy(int[] ratings) {
// 从左往右遍历时的数组
int[] left = new int[ratings.length];
// 从右往左遍历时的数组
int[] right = new int[ratings.length];
// 每个孩子都要分到糖果
Arrays.fill(left, 1);
Arrays.fill(right, 1);
// 首先从左往右遍历,发现相邻的两个学生,右边学生的评分更高,则右边学生比左边学生多一颗糖果。
for (int i = 1; i < ratings.length; i++) {
if (ratings[i] > ratings[i - 1]) {
left[i] = left[i - 1] + 1;
}
}
// 然后从右往左遍历,比较相邻的两个学生,左边学生的评分更高,则左边学生比右边学生多一颗糖果。
// 这里为什么选择从右往左遍历,而不是从左往右遍历?
// 如果从左往右遍历,两个相邻的学生,左边的学生评分比右边学生的评分高,那左边需要比右边多一颗糖果
// 但是如果右边的学生比他右边的学生评分高,此时还会更新糖果数。所以这样遍历不能满足评分高的糖果多。
// 如果从右往左遍历,右边的学生糖果是不会再更新的。
// 例如 4 3 2 从左往右遍历最终糖果会是 2 2 1
for (int i = ratings.length - 2; i >= 0; i--) {
if (ratings[i] > ratings[i + 1]) {
right[i] = right[i + 1] + 1;
}
}
int count = 0;
for (int i = 0; i < ratings.length; i++) {
count = count + Math.max(left[i], right[i]);
}
return count;
}
}
1024. 视频拼接
你将会获得一系列视频片段,这些片段来自于一项持续时长为 time 秒的体育赛事。这些片段可能有所重叠,也可能长度不一。
使用数组 clips 描述所有的视频片段,其中 clips[i] = [starti, endi] 表示:某个视频片段开始于 starti 并于 endi 结束。
甚至可以对这些片段自由地再剪辑:
- 例如,片段 [0, 7] 可以剪切成 [0, 1] + [1, 3] + [3, 7] 三部分。
我们需要将这些片段进行再剪辑,并将剪辑后的内容拼接成覆盖整个运动过程的片段([0, time])。
返回所需片段的最小数目,如果无法完成该任务,则返回 -1 。
class Solution {
int videoStitching(int[][] clips, int T) {
if (T == 0) {
return 0;
}
// 按起点升序排列,起点相同的降序排列。
Arrays.sort(clips, (a, b) -> {
if (a[0] == b[0]) {
return b[1] - a[1];
}
return a[0] - b[0];
});
// 记录选择的短视频个数。
int res = 0;
int curEnd = 0, nextEnd = 0;
int i = 0, n = clips.length;
while (i < n && clips[i][0] <= curEnd) {
// 在第 res 个视频的区间内贪心选择下一个视频。
while (i < n && clips[i][0] <= curEnd) {
nextEnd = Math.max(nextEnd, clips[i][1]);
i++;
}
// 找到下一个视频,更新curEnd。
res++;
curEnd = nextEnd;
if (curEnd >= T) {
// 已经可以拼出区间 [0, T]。
return res;
}
}
// 无法连续拼出区间 [0, T]
return -1;
}
}
回溯
for 选择 in 选择列表:
# 做选择
将该选择从选择列表移除
路径.add(选择)
backtrack(路径, 选择列表)
# 撤销选择
路径.remove(选择)
将该选择再加入选择列表
17. 电话号码的字母组合⭐⭐⭐
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按任意顺序返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
class Solution {
// 设置全局列表存储最后的结果
List<String> list = new ArrayList<>();
// 每次迭代获取一个字符串,所以会涉及大量的字符串拼接,所以这里选择更为高效的 StringBuilder。
StringBuilder sb = new StringBuilder();
public List<String> letterCombinations(String digits) {
// 从题目提示看到digits数组长度可能为0
if (digits == null || digits.length() == 0) {
return list;
}
// 初始对应所有的数字,为了直接对应2-9,新增了两个无效的字符串""。
String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
backTrack(digits, numString, 0);
return list;
}
// 比如digits如果为"23",num 为0,则str表示2对应的 abc。
public void backTrack(String digits, String[] numString, int start) {
// 遍历全部一次记录一次得到的字符串。
if (start == digits.length()) {
list.add(sb.toString());
return;
}
// str 表示当前num对应的字符串。
String str = numString[digits.charAt(start) - '0'];
for (int i = 0; i < str.length(); i++) {
sb.append(str.charAt(i));
backTrack(digits, numString, start + 1);
// 剔除末尾的继续尝试。
sb.deleteCharAt(sb.length() - 1);
}
}
}
22. 括号生成⭐⭐⭐
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
输入:n = 3
输出:["((()))","(()())","(())()","()(())","()()()"]
本题可以改写为:
现在有 2n 个位置,每个位置可以放置字符 ( 或者 ),组成的所有括号组合中,有多少个是合法的?
这就是典型的回溯算法提醒,暴力穷举就行了。
不过为了减少不必要的穷举,我们要知道合法括号串有以下性质:
1、一个「合法」括号组合的左括号数量一定等于右括号数量,这个很好理解。
2、对于一个「合法」的括号字符串组合 p,必然对于任何 0 <= i < len(p) 都有:子串 p[0..i] 中左括号的数量都大于或等于右括号的数量。
因为从左往右算的话,肯定是左括号多嘛,到最后左右括号数量相等,说明这个括号组合是合法的。
class Solution {
List<String> res = new ArrayList<>();
StringBuilder path = new StringBuilder();
public List<String> generateParenthesis(int n) {
backTrack(n, n);
return res;
}
private void backTrack(int left, int right) {
if (right < left) {
return;
}
if (left < 0 || right < 0) {
return;
}
if (left == 0 && right == 0) {
res.add(path.toString());
return;
}
path.append("(");
backTrack(left - 1, right);
path.deleteCharAt(path.length() - 1);
path.append(")");
backTrack(left, right - 1);
path.deleteCharAt(path.length() - 1);
}
}
/**
* 必须要满足两个条件
* 1,括号组合中左括号的数量等于右括号的数量
* 2,括号组合中任何位置左括号的数量都是大于等于右括号的数量
*/
class Solution {
// 做减法
public List<String> generateParenthesis(int n) {
List<String> res = new ArrayList<>();
// 特判
if (n == 0) {
return res;
}
// 执行深度优先遍历,搜索可能的结果
dfs("", n, n, res);
return res;
}
/**
* @param curStr 当前递归得到的结果
* @param left 左括号还有几个可以使用
* @param right 右括号还有几个可以使用
* @param res 结果集
*/
private void dfs(String curStr, int left, int right, List<String> res) {
// 因为每一次尝试,都使用新的字符串变量,所以无需回溯。
// 在递归终止的时候,直接把它添加到结果集即可,注意与「力扣」第 46 题、第 39 题区分。
if (left == 0 && right == 0) {
res.add(curStr);
return;
}
// 剪枝(如图,左括号可以使用的个数严格大于右括号可以使用的个数,才剪枝,注意这个细节)
if (left > right) {
return;
}
if (left > 0) {
dfs(curStr + "(", left - 1, right, res);
}
if (right > 0) {
dfs(curStr + ")", left, right - 1, res);
}
}
}
46. 全排列
给定一个不含重复数字的数组 nums ,返回其所有可能的全排列 。你可以按任意顺序返回答案。
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
回溯的题大多都可以看作树形的结构
从全排列问题开始理解回溯算法
我们尝试在纸上写 3个数字、4个数字、5个数字的全排列,相信不难找到这样的方法。以数组 [1, 2, 3] 的全排列为例。
先写以 1开头的全排列,它们是:[1, 2, 3], [1, 3, 2],即 1 + [2, 3] 的全排列(注意:递归结构体现在这里);
再写以 2开头的全排列,它们是:[2, 1, 3], [2, 3, 1],即 2 + [1, 3] 的全排列;
最后写以 3 开头的全排列,它们是:[3, 1, 2], [3, 2, 1],即 3 + [1, 2] 的全排列。
总结搜索的方法:按顺序枚举每一位可能出现的情况,已经选择的数字在当前要选择的数字中不能出现。按照这种策略搜索就能够做到不重不漏。
这样的思路,可以用一个树形结构表示。每当走到树的底层叶子节点,其「路径」就是一个全排列。
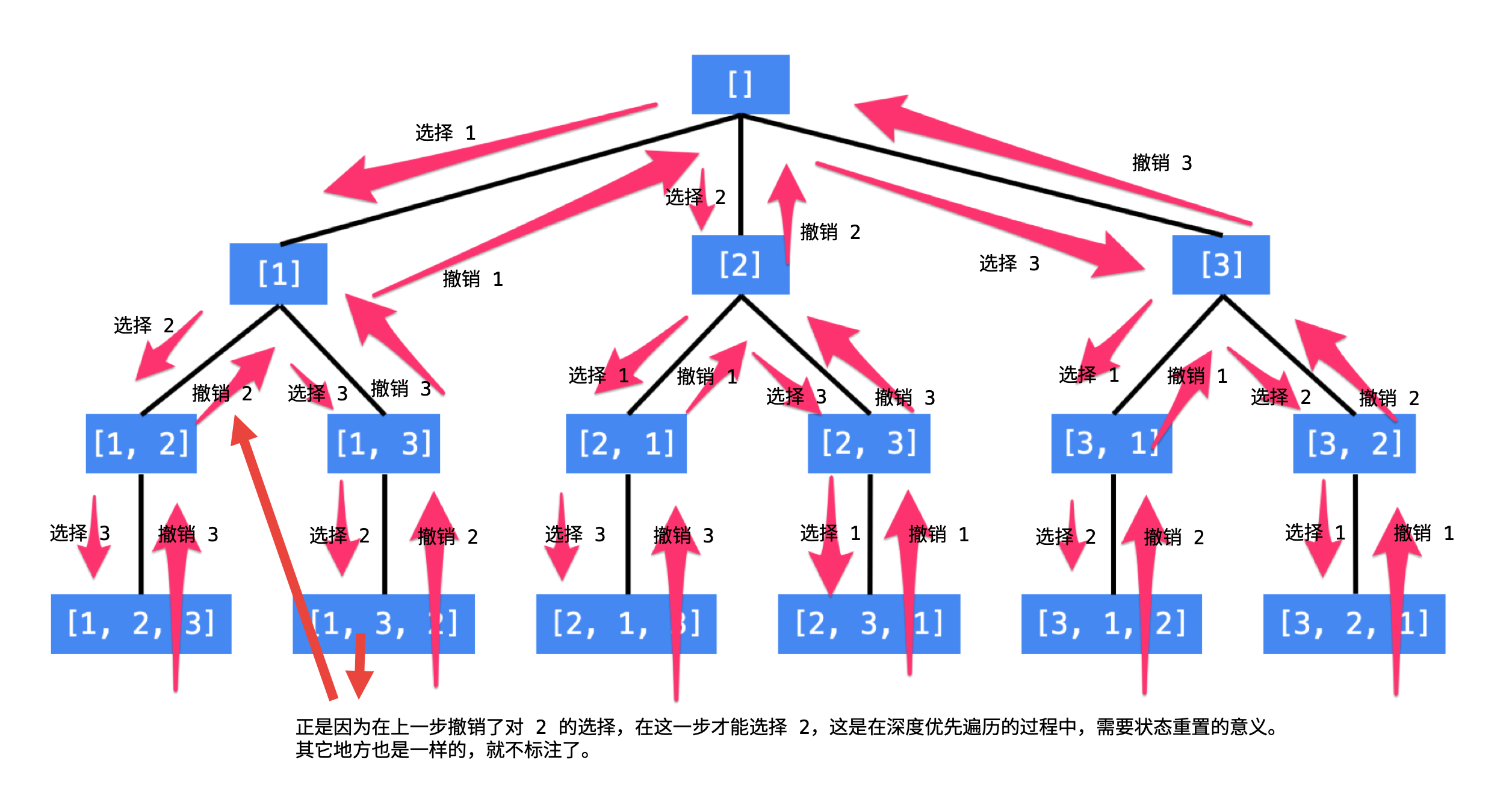
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
backTrack(nums);
return res;
}
private void backTrack(int[] nums) {
// 3、终止条件,如果数字都被使用完了,说明找到了一个排列,(可以把它看做是n叉树到
// 叶子节点了,不能往下走了,所以要返回)
if (path.size() == nums.length) {
// 因为list是引用传递,这里必须要重新new一个,否则在回溯的时候,会删除掉已经加入最终结果集的数据。
res.add(new ArrayList<>(path));
return;
}
//(可以把它看做是遍历n叉树每个节点的子节点)2、选择列表
for (int i = 0; i < nums.length; i++) {
// 排除已经选过的元素
if (path.contains(nums[i])) {
continue;
}
// 选择当前值 1、路径
path.add(nums[i]);
// 递归(可以把它看做遍历子节点的子节点)
backtrack(nums);
// 撤销选择,把最后一次添加的值给移除
path.remove(path.size() - 1);
}
}
}
47. 全排列 II⭐⭐
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
这道题是包含重复的数字
这道题的关键就是如何去重
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> permuteUnique(int[] nums) {
// 先对数组进行排序,这样做目的是相同的值在数组中肯定是挨着的,
// 方便过滤掉重复的结果
Arrays.sort(nums);
// boolean数组,used[i]表示元素nums[i]是否被访问过
boolean[] used = new boolean[nums.length];
// 执行回溯算法
backtrack(nums, used);
return res;
}
/*
一般来说回溯的方法都是没有返回值的
*/
public void backtrack(int[] nums, boolean[] used) {
// 如果数组中的所有元素都使用完了,类似于到了叶子节点,
// 我们直接把从根节点到当前叶子节点这条路径的元素加入
// 到集合res中
if (path.size() == nums.length) {
res.add(new ArrayList<>(path));
return;
}
// 遍历数组中的元素
// 因为排列是讲究顺序的所以这里
for (int i = 0; i < nums.length; i++) {
// 如果已经被使用过,则直接跳过
// 这里不像全排列那样去判断临时结果集中有没有这个数,因为nums序列本来有重复的数。
// 比如有两个相同的数a,第一个a用了添加进path中,如果遇到第二个a时用path.contains(a)判断会以为第二个a也用过了。但实际上还没有用过
// 如果还像全排列那样判断临时结果集会出现错误。
if (used[i]) {
continue;
}
// 注意,这里要剪掉重复的组合
// 如果当前元素和前一个一样,并且前一个没有被使用过,我们也跳过
// 这个判断会保证重复的数,前面的一定要先用掉
if (i > 0 && nums[i - 1] == nums[i] && !used[i - 1]) {
continue;
}
// 否则我们就使用当前元素,把他标记为已使用,相当于从选择列表中移除
used[i] = true;
// 把当前元素nums[i]添加到tempList中
path.add(nums[i]);
// 递归,类似于n叉树的遍历,继续往下走
backtrack(nums, used);
// 递归完之后会往回走,往回走的时候要撤销选择
path.remove(path.size() - 1);
used[i] = false; // 添加回选择列表
}
}
}
怎么样才能过滤掉重复的数字呢,一种方式就是找出所有的组合结果,然后在这个结果中过滤掉重复的组合。如果组合是字符串还好比较,但这里是个数组,所有
数组两两比较复杂度太高,这种方式我们不考虑。
除了上面说的一种解法还有一种方式就是我们常说的剪枝,怎么剪呢?因为要过滤掉重复的,只有重复的数字才会造成重复的结果。所以第一步要做的就是对数组
进行排序,排序之后相同的数字肯定是挨着的。
当遍历到当前数字的时候,如果数组中当前数字和前一个数字一样,并且前一个数字没有被使用,我们就跳过当前分支,也就是把当前分支给剪掉。如下图所示
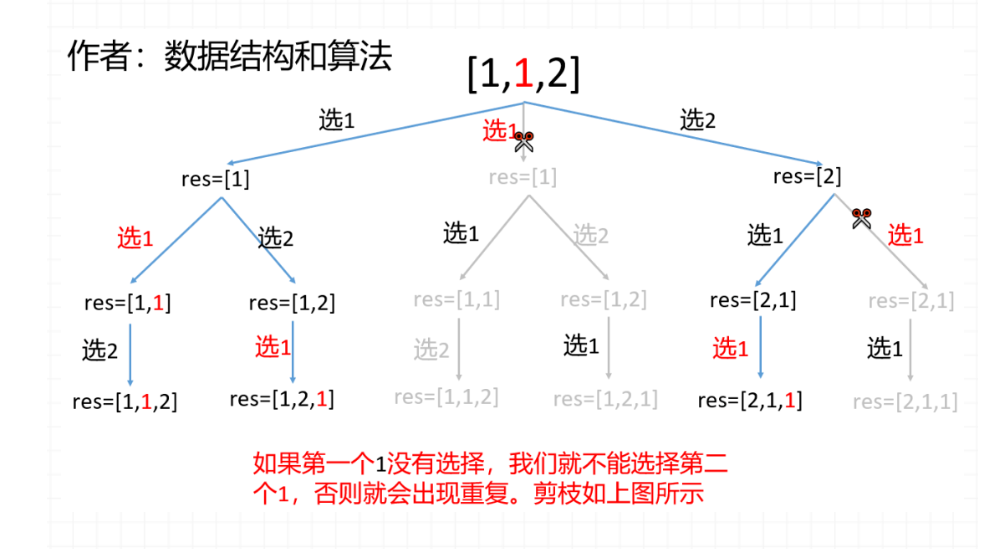
51. N 皇后⭐⭐
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
首先我们来分析一下。对于每一行,我们可以有 n 个选择,即任选一个格放下棋子,只要满足要求即可;同时,我们需要做 n 次这样的选择,即存在 n 行,每一
行选择一个格子放棋子
N 皇后的决策树如下图所示:

很不巧的是,n = 3 时,没有一种情况是符合的。不过这不重要!!!(如上图红色标注的分支均为不符合条件的情况)
问题一:用什么数据来表示棋盘呢???
回答一:二维数组。.表示未放棋子;Q表示放了棋子
问题二:如何判断当前行某一格放下棋子是满足要求的呢??
回答二:具体代码如下:
class Solution {
private List<String> list = new ArrayList<>();
private List<List<String>> result = new ArrayList<>();
public List<List<String>> solveNQueens(int n) {
// 只给了皇后的数量,初始化一个二维的字符数组。
char[][] board = new char[n][n];
// 初始化棋盘
for (int i = 0; i < n; i++) {
Arrays.fill(board[i], '.');
}
// 从第 0 行开始
backtrack(board, 0);
return result;
}
private void backtrack(char[][] board, int row) {
// 满足要求
if (list.size() == board.length) {
result.add(new ArrayList<>(list));
return;
}
for (int i = 0; i < board.length; i++) {
// 该格不符合放棋子的条件
if (!isValid(board, row, i)) {
continue;
}
// 放棋子
board[row][i] = 'Q';
// 记录当前行的数据
list.add(new String(board[row]));
// 处理下一行
backtrack(board, row + 1);
// 移除棋子
board[row][i] = '.';
// 去除当前行的数据
list.remove(list.size() - 1);
}
}
private boolean isValid(char[][] board, int row, int col) {
int n = board.length;
// 检查列是否有冲突
for (int i = 0; i <= row; i++) {
if (board[i][col] == 'Q') {
return false;
}
}
// 检查右上方是否有冲突
for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (board[i][j] == 'Q') {
return false;
}
}
// 检查左上方是否有冲突
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (board[i][j] == 'Q') {
return false;
}
}
return true;
}
}
77. 组合
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
不同于全排列,组合是不能够出现重复的。
解题思路:
如果你能够成功的生成所有无重子集,那么你稍微改改代码就能生成所有无重组合了。
你比如说,让你在 nums = [1,2,3] 中拿 2 个元素形成所有的组合,你怎么做?
稍微想想就会发现,大小为 2 的所有组合,不就是所有大小为 2 的子集嘛。
所以我说组合和子集是一样的:大小为 k 的组合就是大小为 k 的子集。
class Solution {
List<List<Integer>> res = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> combine(int n, int k) {
backtrack(n, k, 1);
return res;
}
/**
* 每次从集合中选取元素,可选择的范围随着选择的进行而收缩,调整可选择的范围,就是要靠startIndex。
*
* @param startIndex 用来记录本层递归中,集合从哪里开始遍历。
*/
private void backtrack(int n, int k, int startIndex) {
// 3、终止条件
if (path.size() == k) {
res.add(new ArrayList<>(path));
return;
}
// k - path.size()表示当前路径中还需要多少个元素才能构成k个数的组合。
// n - i + 1表示在当前路径中还可以往下遍历的节点的数量
// 找出搜索起点上界
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) {
path.add(i); // 1、路径
backtrack(n, k, i + 1);
path.removeLast();
}
}
}
事实上,如果 n = 5, k = 3,从 4开始搜索就已经没有意义了,这是因为:即使把 4 选上,后面的数只有 5,一共就 2个候选数,凑不出3个数的组合。因此,搜索
起点有上界,这个上界是多少,可以举几个例子分析。
分析搜索起点的上界,其实是在深度优先遍历的过程中剪枝,剪枝可以避免不必要的遍历,剪枝剪得好,可以大幅度节约算法的执行时间。
下面的图片绿色部分是剪掉的枝叶,当 n 很大的时候,能少遍历很多结点,节约了时间。

容易知道:搜索起点和当前还需要选几个数有关,而当前还需要选几个数与已经选了几个数有关,即与 path 的长度相关。我们举几个例子分析:
例如:n = 5 ,k = 3
path.size() == 0 的时候,接下来要选择3个数,搜索起点最大是3,最后一个被选的组合是 [3, 4, 5];
path.size() == 1 的时候,接下来要选择2个数,搜索起点最大是4,最后一个被选的组合是 [4, 5];
path.size() == 2 的时候,接下来要选择1个数,搜索起点最大是5,最后一个被选的组合是 [5];
可以归纳出:
搜索起点的上界 + 接下来要选择的元素个数 - 1 = n 上面的例子是 3 + 3 = 6 6 - 1= 5 = n
其中,接下来要选择的元素个数 = k - path.size(),整理得到:
搜索起点的上界 = n - (k - path.size()) + 1
39. 组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式
返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
backtrack(candidates, 0, target);
return res;
}
private void backtrack(int[] candidates, int start, int target) {
// 找到一个满足条件的组合,加入最终的结果集
if (target == 0) {
res.add(new ArrayList<>(path));
return;
}
// 因为可以选择重复的数,所以每次进入backtrack当前数及之后的数都可以选择
for (int i = start; i < candidates.length; i++) {
if (candidates[i] <= target) {
path.add(candidates[i]);
backtrack(candidates, i, target - candidates[i]);
path.remove(path.size() - 1); // 回溯
}
}
}
}
40. 组合总和 II⭐⭐
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。注意:解集不能包含重复的组合。
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
// 关键步骤,对候选数组进行排序,让相同的数挨在一起。
Arrays.sort(candidates);
boolean[] used = new boolean[candidates.length];
dfs(candidates, used, 0, target);
return res;
}
private void dfs(int[] candidates, boolean[] used, int begin, int target) {
if (target == 0) {
res.add(new ArrayList<>(path));
return;
}
for (int i = begin; i < candidates.length; i++) {
if (candidates[i] <= target) {
// 去重逻辑,如果存在相同的数,前一个数没有使用,当前这个数是不能使用的,否则会出现重复。
if (i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]) {
continue;
}
// 做选择
path.add(candidates[i]);
// 从选择列表中移除
used[i] = true;
dfs(candidates, used, i + 1, target - candidates[i]);
path.remove(path.size() - 1);
used[i] = false;
}
}
}
}
216. 组合总和 III⭐⭐
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
- 只使用数字1到 9
- 每个数字最多使用一次
返回所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
回溯其实就是递归,反正我暂时是这么理解的。我们都知道递归就是调用同样的方法(自己调用自己),最重要的核心就是执行相同的逻辑
这题说的很明白,就是从1-9中选出k个数字,他们的和等于n,并且这k个数字不能有重复的。所以第一次选择的时候可以从这9个数字中任选一个,沿着这个分支
走下去,第二次选择的时候还可以从这9个数字中任选一个,但因为不能有重复的,所以要排除第一次选择的,第二次选择的时候只能从剩下的8个数字中选一
个……。这个选择的过程就比较明朗了,我们可以把它看做一棵9叉树,除叶子结点外每个节点都有9个子节点,也就是下面这样

从9个数字中任选一个,就是沿着他的任一个分支一直走下去,其实就是DFS。
二叉树的DFS代码是下面这样的
public static void TreeDFS(TreeNode root) {
if (root == null) {
return;
}
TreeDFS(root.left);
TreeDFS(root.right);
}
这里可以仿照二叉树的DFS来写一下9叉树,9叉树的DFS就是通过递归遍历他的9个子节点,代码如下:
public static void TreeDFS(TreeNode root) {
// 递归必须有终止条件
if (root == null) {
return;
}
System.out.println(root.val);
// 通过循环分别遍历9个数
for (int i = 1; i <= 9; i++) {
// 一些操作
TreeDFS("第i个子节点")
}
}
DFS其实就相当于遍历他的所有分支,就是列出他所有的可能结果,只要判断结果等于n就是我们要找的,那么这棵9叉树最多有多少层呢,因为有k个数字,所以
最多只能有k 层。来看下代码
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> combinationSum3(int k, int n) {
backtrack(1, k, n);
return res;
}
private void backtrack(int start, int k, int n) {
// 这里不但要判断path集合中的数是否是k个,而且还要判断k个数的和是否是n
if (path.size() == k && n == 0) {
res.add(new ArrayList<>(path));
return;
}
for (int i = start; i <= 9; i++) {
if (i <= n) {
path.add(i);
backtrack(i + 1, k, n - i);
path.remove(path.size() - 1);
} else {
break;
}
}
}
}
79. 单词搜索⭐⭐(有返回值)
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。
同一个单元格内的字母不允许被重复使用。
class Solution {
public boolean exist(char[][] board, String word) {
char[] words = word.toCharArray();
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
// 从[i,j]这个坐标开始查找
if (dfs(board, words, i, j, 0)) {
return true;
}
}
}
return false;
}
private boolean dfs(char[][] board, char[] word, int i, int j, int index) {
// 首先是4个边界的判断,如果越界直接返回false。index表示的是查找到字符串word的第几个字符,
// 如果这个字符不等于board[i][j],说明验证这个坐标路径是走不通的,直接返回false。
if (i >= board.length || i < 0 || j >= board[0].length || j < 0 || board[i][j] != word[index]) {
return false;
}
// 如果word的每个字符都查找完了,直接返回true。
if (index == word.length - 1) {
return true;
}
// 把当前坐标的值保存下来,为了在最后复原
char tmp = board[i][j];
// 然后修改当前坐标的值 来到这里说明和word的某个字符匹配上了
board[i][j] = '*';
// 走递归,沿着当前坐标的上下左右4个方向查找
boolean res = dfs(board, word, i + 1, j, index + 1) // 往下走
|| dfs(board, word, i - 1, j, index + 1) // 往上走
|| dfs(board, word, i, j + 1, index + 1) // 往右走
|| dfs(board, word, i, j - 1, index + 1); // 往左走
// 递归之后再把当前的坐标复原
board[i][j] = tmp; // 假如一直匹配着走,突然匹配到一个几个方向都走不通了,此时需要将原来走过的路径元素复原
return res;
}
}
212. 单词搜索 II(Trie辅助)⭐⭐⭐⭐
给定一个 m x n 二维字符网格 board 和一个单词(字符串)列表 words, 返回所有二维网格上的单词。
单词必须按照字母顺序,通过 相邻的单元格 内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。
同一个单元格内的字母在一个单词中不允许被重复使用。
参考题解:https://leetcode.cn/problems/word-search-ii/solution/tong-ge-lai-shua-ti-la-yi-ti-si-jie-zi-d-2igi/
class Solution {
// 上下左右移动的方向
int[][] dirs = new int[][]{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
StringBuilder result = new StringBuilder();
public List<String> findWords(char[][] board, String[] words) {
// 结果集,去重
Set<String> resultSet = new HashSet<>();
// 构建字典树
TrieNode root = buildTrie(words);
// 记录沿途遍历到的元素
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
// 从每个元素开始遍历
dfs(resultSet, board, i, j, root);
}
}
// 题目要求返回List
return new ArrayList<>(resultSet);
}
private void dfs(Set<String> resultSet, char[][] board, int i, int j, TrieNode node) {
// 判断越界,或者访问过,或者不在字典树中,直接返回。
if (i < 0 || j < 0 || i >= board.length || j >= board[0].length || board[i][j] == '*' || node.children[board[i][j] - 'a'] == null) {
return;
}
// 记录当前字符。
char curr = board[i][j];
result.append(curr);
// 如果有结束字符,加入结果集中。
if (node.children[curr - 'a'].isEnd) {
resultSet.add(result.toString());
}
// 记录当前元素已访问。
board[i][j] = '*';
// 按四个方向去遍历。
for (int[] dir : dirs) {
dfs(resultSet, board, i + dir[0], j + dir[1], node.children[curr - 'a']);
}
// 还原状态。
board[i][j] = curr;
result.deleteCharAt(result.length() - 1);
}
private TrieNode buildTrie(String[] words) {
// root是最上面一层的节点。
TrieNode root = new TrieNode();
for (String word : words) {
char[] arr = word.toCharArray();
TrieNode curr = root;
for (char c : arr) {
if (curr.children[c - 'a'] == null) {
curr.children[c - 'a'] = new TrieNode();
}
curr = curr.children[c - 'a'];
}
curr.isEnd = true;
}
return root;
}
class TrieNode {
// 记录到这个节点是否是一个完整的单词。
boolean isEnd = false;
// 孩子节点,题目说了都是小写字母,所以用数组,否则可以用HashMap替换。
TrieNode[] children = new TrieNode[26];
}
}
980. 不同路径 III⭐⭐⭐⭐
在二维网格 grid 上,有 4 种类型的方格:
- 1 表示起始方格。且只有一个起始方格。
- 2 表示结束方格,且只有一个结束方格。
- 0 表示我们可以走过的空方格。
- -1 表示我们无法跨越的障碍。
返回在四个方向(上、下、左、右)上行走时,从起始方格到结束方格的不同路径的数目。
每一个无障碍方格都要通过一次,但是一条路径中不能重复通过同一个方格。
参考题解:https://leetcode.cn/problems/unique-paths-iii/solution/dfs-hui-su-shuang-bai-by-quantum-10/
class Solution {
public int uniquePathsIII(int[][] grid) {
int startX = 0, startY = 0, stepNum = 1; // 当grid[i][j] == 2, stepNum++, 这里直接初始化为1。
// 遍历获取起始位置和统计总步数
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == 1) {
startX = i;
startY = j;
continue;
}
// 统计空白格的数量。
if (grid[i][j] == 0) {
stepNum++;
}
}
}
return dfs(startX, startY, stepNum, grid);
}
public int dfs(int x, int y, int stepSur, int[][] grid) {
// 排除越界的情况和遇到障碍的情况
if (x < 0 || x >= grid.length || y < 0 || y >= grid[0].length || grid[x][y] == -1) {
return 0;
}
// 到达结束方格
if (grid[x][y] == 2) {
// 所有空方格是否已经走完,没走完就达到了结束方格这样可不算一条路径。
return stepSur == 0 ? 1 : 0;
}
// 已走过的标记为障碍
grid[x][y] = -1;
int res = 0;
res += dfs(x - 1, y, stepSur - 1, grid);
res += dfs(x + 1, y, stepSur - 1, grid);
res += dfs(x, y - 1, stepSur - 1, grid);
res += dfs(x, y + 1, stepSur - 1, grid);
// dfs遍历完该位置为起始位置的情况后,置零,以不影响后面的dfs
grid[x][y] = 0;
return res;
}
}
78. 子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集不能包含重复的子集。你可以按任意顺序返回解集。
如果把子集问题、组合问题、分割问题都抽象为一棵树的话,那么组合问题和分割问题都是收集树的叶子节点,而子集问题是找树的所有节点!
其实子集也是一种组合问题,因为它的集合是无序的,子集{1,2} 和子集{2,1}是一样的。
那么既然是无序,取过的元素不会重复取,写回溯算法的时候,for就要从startIndex开始,而不是从0开始!
有同学问了,什么时候for可以从0开始呢?
求排列问题的时候,就要从0开始,因为集合是有序的,{1, 2} 和{2, 1}是两个集合。
以示例中nums = [1,2,3]为例把求子集抽象为树型结构,如下:
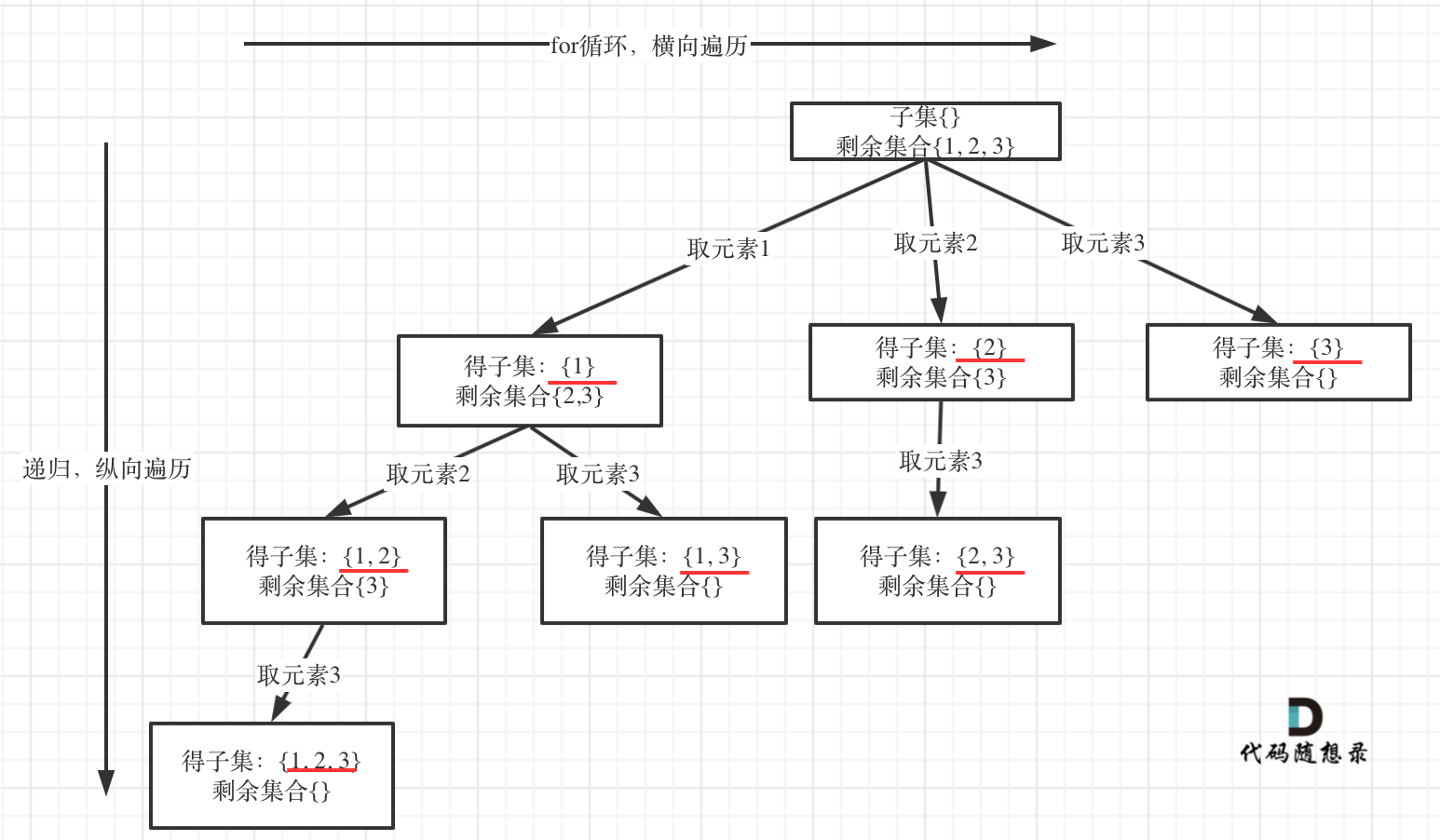
从图中红线部分,可以看出遍历这个树的时候,把所有节点都记录下来,就是要求的子集集合。
剩余集合为空的时候,就是叶子节点。
那么什么时候剩余集合为空呢?
就是startIndex已经大于数组的长度了,就终止了,因为没有元素可取了,代码如下:
if (startIndex >= nums.size()) {
return;
}
其实可以不需要加终止条件,因为startIndex >= nums.size(),本层for循环本来也结束了。
求取子集问题,不需要任何剪枝!因为子集就是要遍历整棵树。
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> subsets(int[] nums) {
backtrack(0, nums);
return res;
}
private void backtrack(int start, int[] nums) {
res.add(new ArrayList<>(path));
for (int i = start; i < nums.length; i++) {
path.add(nums[i]);
backtrack(i + 1, nums);
path.remove(path.size() - 1);
}
}
}
90. 子集 II🏳🌈
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集不能包含重复的子集。返回的解集中,子集可以按任意顺序排列。
输入:nums = [1,2,2]
输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> subsetsWithDup(int[] nums) {
Arrays.sort(nums);
boolean[] used = new boolean[nums.length];
backtrack(0, used, nums);
return res;
}
private void backtrack(int start, boolean[] used, int[] nums) {
res.add(new ArrayList<>(path));
for (int i = start; i < nums.length; i++) {
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
continue;
}
path.add(nums[i]);
used[i] = true;
backtrack(i + 1, used, nums);
path.remove(path.size() - 1);
used[i] = false;
}
}
}
131. 分割回文串⭐👶
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
本题这涉及到两个关键问题:
切割问题,有不同的切割方式
判断回文
相信这里不同的切割方式可以搞懵很多同学了。
这种题目,想用for循环暴力解法,可能都不那么容易写出来,所以要换一种暴力的方式,就是回溯。
一些同学可能想不清楚回溯究竟是如何切割字符串呢?
我们来分析一下切割,其实切割问题类似组合问题。
例如对于字符串abcdef:
组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中在选组第三个。
切割问题:切割一个a之后,在bcdef中再去切割第二段,切割b之后在cdef中在切割第三段。
感受出来了不?
所以切割问题,也可以抽象为一颗树形结构,如图:

class Solution {
List<List<String>> res = new ArrayList<>();
List<String> path = new ArrayList<>();
public List<List<String>> partition(String s) {
backtrack(s, 0);
return res;
}
private void backtrack(String s, int start) {
// 如果起始位置大于s的大小,说明找到了一组分割方案。
if (start == s.length()) {
res.add(new ArrayList(path));
return;
}
for (int i = start; i < s.length(); i++) {
// 如果是回文子串,则记录
if (isPalindrome(s, start, i)) {
String str = s.substring(start, i + 1);
path.add(str);
// 起始位置后移,保证不重复
backtrack(s, i + 1);
path.remove(path.size() - 1);
}
}
}
// 判断是否是回文串
private boolean isPalindrome(String s, int startIndex, int end) {
for (int i = startIndex, j = end; i < j; i++, j--) {
if (s.charAt(i) != s.charAt(j)) {
return false;
}
}
return true;
}
}
递归用来纵向遍历,for循环用来横向遍历,切割线(就是图中的红线)切割到字符串的结尾位置,说明找到了一个切割方法。
此时可以发现,切割问题的回溯搜索的过程和组合问题的回溯搜索的过程是差不多的。
140. 单词拆分 II👶
给定一个字符串 s 和一个字符串字典 wordDict ,在字符串 s 中增加空格来构建一个句子,使得句子中所有的单词都在词典中。以任意顺序 返回所有这些可能
的句子。注意:词典中的同一个单词可能在分段中被重复使用多次。
输入:s = "catsanddog", wordDict = ["cat","cats","and","sand","dog"]
输出:["cats and dog","cat sand dog"]
class Solution {
// 用于存储子串的临时List
public List<String> temp = new ArrayList<>();
// 用于存储结果的List
public List<String> res = new ArrayList<>();
public List<String> wordBreak(String s, List<String> wordDict) {
//使用回溯算法
help(s, wordDict, 0);
return res;
}
// 实现回溯算法的代码,i表示当前该从哪个位置扫描字符串
public void help(String s, List<String> wordDict, int i) {
// 如果字符串扫描结束,那么将temp中的子串合并成一个完整的字符串,添加到结果集中返回
if (i == s.length()) {
StringBuilder sb = new StringBuilder();
for (String str : temp) {
sb.append(str);
}
res.add(sb.toString());
}
// 扫描剩余的字符串
for (int j = i; j < s.length(); j++) {
// 子串出现在了字典中,那么添加到临时List中
if (wordDict.contains(s.substring(i, j + 1))) {
// 添加的时候注意空格的要求
if (j + 1 >= s.length()) {
temp.add(s.substring(i, j + 1));
} else {
temp.add(s.substring(i, j + 1) + " ");
}
// 递归寻找字符串的剩余部分
help(s, wordDict, j + 1);
// 最重要的回溯部分
temp.remove(temp.size() - 1);
}
}
}
}
93. 复原 IP 地址
有效IP地址正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
例如:"0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址,但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效 IP 地址。
给定一个只包含数字的字符串 s ,用以表示一个 IP 地址,返回所有可能的有效 IP 地址,这些地址可以通过在 s 中插入 '.' 来形成。你不能重新排序或删除 s 中的
任何数字。你可以按任何顺序返回答案。
class Solution {
List<String> res = new ArrayList<>();
List<String> path = new ArrayList<>();
public List<String> restoreIpAddresses(String s) {
backTrack(0, s);
return res;
}
private void backTrack(int start, String s) {
if (path.size() == 4 && start != s.length()) {
return;
}
if (path.size() == 4) {
// 将path中的元素以.为分割符连接起来
res.add(String.join(".", path));
}
for (int i = start; i < s.length(); i++) {
String str = s.substring(start, i + 1);
// 去除包含前导0的,以及长度大于3的
// str.length() > 1 && str.startsWith("0")不会去除单独的0。
if (str.length() > 1 && str.startsWith("0") || str.length() > 3) {
continue;
}
int value = Integer.parseInt(str);
if (value > 255) {
continue;
}
path.add(str);
backTrack(i + 1, s);
path.remove(path.size() - 1);
}
}
}
491. 递增子序列(注意去重操作)🏳🌈
给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中至少有两个元素 。
你可以按任意顺序返回答案。
数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一种特殊情况。
示例 1:
输入:nums = [4,6,7,7]
输出:[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]
示例 2:
输入:nums = [4,4,3,2,1]
输出:[[4,4]]
这题的示例1非常具有诱导性,它给出的数组是升序的,导致我们认为用之前那种used数组来去重的办法。这道题的关键在于如何去重。
这个递增子序列比较像是取有序的子集。而且本题也要求不能有相同的递增子序列。
这又是子集,又是去重,是不是不由自主的想起了刚刚讲过的90.子集II。
就是因为太像了,更要注意差别所在,要不就掉坑里了!
在90.子集II中我们是通过排序,再加一个标记数组来达到去重的目的。
而本题求自增子序列,是不能对原数组进行排序的,排完序的数组都是自增子序列了。
所以不能使用之前的去重逻辑!
本题给出的示例,还是一个有序数组 [4, 6, 7, 7],这更容易误导大家按照排序的思路去做了。
为了有鲜明的对比,我用 [4, 7, 6, 7] 这个数组来举例,抽象为树形结构如图:
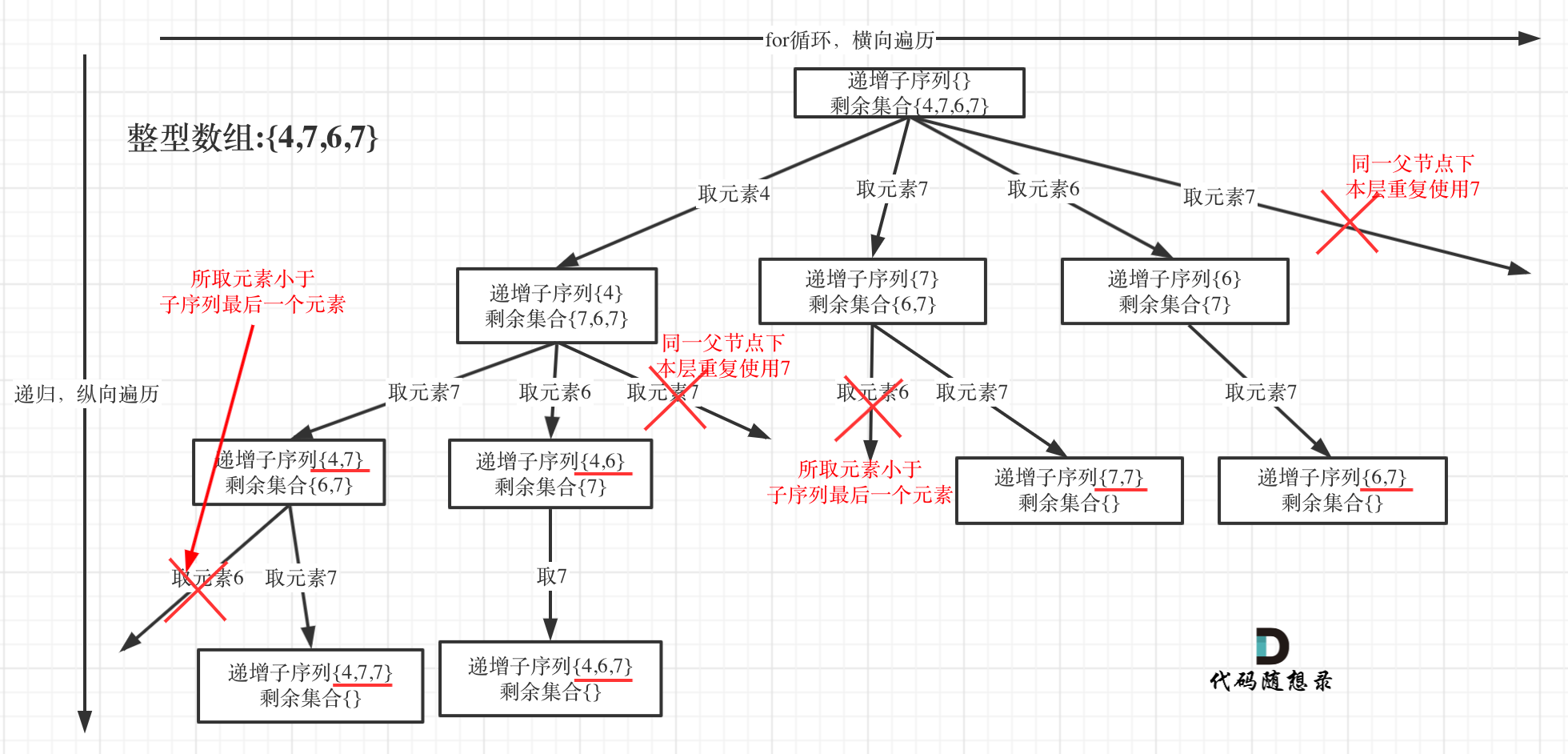
本题其实类似求子集问题,也是要遍历树形结构找每一个节点,所以和回溯算法:求子集问题!一样,可以不加终止条件,startIndex每次都会加1,并不会无限
递归。但本题收集结果有所不同,题目要求递增子序列大小至少为2,所以代码如下:
if (path.size() > 1) {
res.add(new ArrayList<>(path));
// 注意这里不要加return,因为要取树上的所有节点
}
在图中可以看出,同一父节点下的同层上使用过的元素就不能在使用了
那么单层搜索代码如下:
// 使用数组来进行去重
int[] used = new int[201];
for (int i = start; i < nums.length; i++) {
// 当临时集合中末尾的元素大于当前遍历的元素时 或者 相同的数前面已经用过了
if (path.size() != 0 && nums[i] < path.get(path.size() - 1) || (used[nums[i] + 100] == 1)) {
continue;
}
used[nums[i] + 100] = 1;
path.add(nums[i]);
backtracking(nums, i + 1);
path.remove(path.size() - 1);
}
其实用数组来做哈希,效率就高了很多。
注意题目中说了,数值范围[-100,100],所以完全可以用数组来做哈希。
class Solution {
List<Integer> path = new ArrayList<>();
List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> findSubsequences(int[] nums) {
backtracking(nums, 0);
return res;
}
private void backtracking(int[] nums, int start) {
if (path.size() > 1) {
res.add(new ArrayList<>(path));
}
// 使用数组来进行去重
int[] used = new int[201];
for (int i = start; i < nums.length; i++) {
// 当临时集合中末尾的元素大于当前遍历的元素时 或者 相同的数前面已经用过了
if (path.size() != 0 && nums[i] < path.get(path.size() - 1) || (used[nums[i] + 100] == 1)) {
continue;
}
used[nums[i] + 100] = 1;
path.add(nums[i]);
backtracking(nums, i + 1);
path.remove(path.size() - 1);
}
}
}
class Solution {
public List<List<Integer>> findSubsequences(int[] nums) {
backtrack(nums, 0);
return res;
}
List<List<Integer>> res = new LinkedList<>();
// 记录回溯的路径
LinkedList<Integer> track = new LinkedList<>();
// 回溯算法主函数
void backtrack(int[] nums, int start) {
if (track.size() >= 2) {
// 找到一个合法答案
res.add(new LinkedList<>(track));
}
// 用哈希集合防止重复选择相同元素
HashSet<Integer> used = new HashSet<>();
// 回溯算法标准框架
for (int i = start; i < nums.length; i++) {
// 保证集合中元素都是递增顺序
if (!track.isEmpty() && track.getLast() > nums[i]) {
continue;
}
// 保证不要重复使用相同的元素
if (used.contains(nums[i])) {
continue;
}
// 选择 nums[i]
used.add(nums[i]);
track.add(nums[i]);
// 递归遍历下一层回溯树
backtrack(nums, i + 1);
// 撤销选择 nums[i]
track.removeLast();
}
}
}
698. 划分为k个相等的子集(如何穷举以及剪枝的奥秘且有返回值)⭐⭐⭐⭐⭐
给定一个整数数组 nums 和一个正整数 k,找出是否有可能把这个数组分成 k 个非空子集,其总和都相等。
输入: nums = [4, 3, 2, 3, 5, 2, 1], k = 4
输出: True
说明: 有可能将其分成 4 个子集(5),(1,4),(2,3),(2,3)等于总和。
这道题是非常经典的一道回溯算法题。
参考题解:https://leetcode.cn/problems/partition-to-k-equal-sum-subsets/solution/by-lfool-d9o7/
球选择桶:
class Solution {
public boolean canPartitionKSubsets(int[] nums, int k) {
int sum = 0;
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
}
if (sum % k != 0) {
return false;
}
Integer[] numsMirror = new Integer[nums.length];
for (int i = 0; i < nums.length; i++) {
numsMirror[i] = nums[i];
}
// Integer数组降序排列
Arrays.sort(numsMirror, Collections.reverseOrder());
int target = sum / k;
int[] bucket = new int[k];
return backtrack(numsMirror, 0, bucket, k, target);
}
// 球选桶
// index : 第 index 个球开始做选择
// bucket : 桶
private boolean backtrack(Integer[] numsMirror, int index, int[] bucket, int k, int target) {
// 结束条件:已经处理完所有球,所有球都做出了选择。
// 因为桶容量之和就是数组之和,当遍历完数组之后,说明所有桶都装满了。
if (index == numsMirror.length) {
return true;
}
// nums[index] 开始做选择
for (int i = 0; i < k; i++) {
// 对于第一个球,任意放到某个桶中的效果都是一样的,所以我们规定放到第一个桶中。
if (i > 0 && index == 0) {
break;
}
// 其他逻辑不变
// 如果当前桶和上一个桶内的元素和相等,则跳过
// 原因:如果元素和相等,那么 nums[index] 选择上一个桶和选择当前桶可以得到的结果是一致的。
if (i > 0 && bucket[i] == bucket[i - 1]) {
continue;
}
// 其他逻辑不变
// 剪枝:放入球后超过 target 的值,选择下一个桶。
if (bucket[i] + numsMirror[index] > target) {
continue;
}
// 做选择:放入 i 号桶。
bucket[i] += numsMirror[index];
// 处理下一个球,即 nums[index + 1]
if (backtrack(numsMirror, index + 1, bucket, k, target)) {
return true;
}
// 撤销选择:挪出 i 号桶。
bucket[i] -= numsMirror[index];
}
// k 个桶都不满足要求。
return false;
}
}
// @solution-sync:end
class Main {
public static void main(String[] args) {
int[] nums = new int[]{5, 5, 4, 3, 3, 2, 2};
int k = 4;
boolean result = new Solution().canPartitionKSubsets(nums, k);
System.out.println(result);
}
}
桶选择球:
class Solution {
public boolean canPartitionKSubsets(int[] nums, int k) {
if (k > nums.length) {
return false;
}
int sum = 0;
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
}
if (sum % k != 0) {
return false;
}
int used = 0;
int target = sum / k;
return backtrack(k, 0, nums, 0, used, target);
}
HashMap<Integer, Boolean> memo = new HashMap<>();
boolean backtrack(int k, int bucket, int[] nums, int start, int used, int target) {
// base case
if (k == 0) {
// 所有桶都被装满了,而且 nums 一定全部用完了。
return true;
}
if (bucket == target) {
// 装满了当前桶,递归穷举下一个桶的选择。
// 让下一个桶从 nums[0] 开始选数字。
boolean res = backtrack(k - 1, 0, nums, 0, used, target);
// 缓存结果。
memo.put(used, res);
return res;
}
if (memo.containsKey(used)) {
// 避免冗余计算。
return memo.get(used);
}
for (int i = start; i < nums.length; i++) {
// 剪枝
if (((used >> i) & 1) == 1) { // 判断第 i 位是否是 1。
// nums[i] 已经被装入别的桶中。
continue;
}
if (nums[i] + bucket > target) {
continue;
}
// 做选择
used |= 1 << i; // 将第 i 位置为 1。
bucket += nums[i];
// 递归穷举下一个数字是否装入当前桶。
if (backtrack(k, bucket, nums, i + 1, used, target)) {
return true;
}
// 撤销选择
used ^= 1 << i; // 使用异或运算将第 i 位恢复 0。
bucket -= nums[i];
}
return false;
}
}
class Main {
public static void main(String[] args) {
int[] nums = new int[]{5, 5, 4, 3, 3, 2, 2};
int k = 4;
boolean result = new Solution().canPartitionKSubsets(nums, k);
System.out.println(result);
}
}
37. 解数独⭐⭐⭐
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
- 数字 1-9 在每一行只能出现一次。
- 数字 1-9 在每一列只能出现一次。
- 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 '.' 表示。
class Solution {
int m = 9, n = 9;
public void solveSudoku(char[][] board) {
backtrack(board, 0, 0);
}
boolean backtrack(char[][] board, int i, int j) {
if (j == n) {
// 穷举到最后一列的话就换到下一行重新开始。
return backtrack(board, i + 1, 0);
}
if (i == m) {
// 找到一个可行解,触发 base case
return true;
}
if (board[i][j] != '.') {
// 如果有预设数字,不用我们穷举
return backtrack(board, i, j + 1);
}
for (char ch = '1'; ch <= '9'; ch++) {
// 如果遇到不合法的数字,就跳过
if (isValid(board, i, j, ch)) {
board[i][j] = ch;
// 如果找到一个可行解,立即结束。逐层返回。
if (backtrack(board, i, j + 1)) {
return true;
}
board[i][j] = '.';
}
}
// 穷举完 1~9,依然没有找到可行解,此路不通
return false;
}
// 判断 board[i][j] 是否可以填入 n
boolean isValid(char[][] board, int row, int col, char n) {
for (int i = 0; i < 9; i++) {
// 判断行是否存在重复
if (board[row][i] == n) {
return false;
}
// 判断列是否存在重复
if (board[i][col] == n) {
return false;
}
// 判断 3 x 3 方框是否存在重复
int startRow = (row / 3) * 3;
int startCol = (col / 3) * 3;
for (int i = startRow; i < startRow + 3; i++) {
for (int j = startCol; j < startCol + 3; j++) {
if (board[i][j] == ch) {
return false;
}
}
}
return true;
}
}
树相关
https://labuladong.gitee.io/algo/2/21/36/
144. 二叉树的前序遍历
递归写法:
class Solution {
ArrayList<Integer> list = new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {
if (root == null) {
return list;
}
list.add(root.val);
preorderTraversal(root.left);
preorderTraversal(root.right);
return list;
}
}
迭代写法:
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null) {
return result;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
result.add(node.val);
// 右子树先入栈
if (node.right != null) {
stack.push(node.right);
}
if (node.left != null) {
stack.push(node.left);
}
}
return result;
}
}
94. 二叉树的中序遍历
递归写法:
class Solution {
List<Integer> res = new ArrayList<>();
public List<Integer> inorderTraversal(TreeNode root) {
if (root == null) {
return res;
}
inorderTraversal(root.left);
res.add(root.val);
inorderTraversal(root.right);
return res;
}
}
迭代写法:
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) {
return res;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode node = root;
// 迭代的思想是利用栈(递归不也是函数调用栈吗)
// 一直把左节点入栈,当node第一次为null时说明已经来到了最左边
// 这时候走else分支,弹出最左边的元素,遍历它的值。
// 然后查看它是否有右子节点,有就加入栈中,没有就继续弹栈。
while (node != null || !stack.isEmpty()) {
if (node != null) {
stack.push(node);
node = node.left;
} else {
node = stack.pop();
res.add(node.val);
// 注意这里是把刚出栈的节点右孩子赋值给node
node = node.right;
}
}
return res;
}
}
145. 二叉树的后序遍历
递归写法:
class Solution {
List<Integer> res = new ArrayList<>();
public List<Integer> postorderTraversal(TreeNode root) {
if (root == null) {
return res;
}
postorderTraversal(root.left);
postorderTraversal(root.right);
res.add(root.val);
return res;
}
}
迭代写法:
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) {
return res;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
res.add(node.val);
// 向将左节点入栈,待会儿就后出栈,也就后遍历。
if (node.left != null) {
stack.push(node.left);
}
if (node.right != null) {
stack.push(node.right);
}
}
Collections.reverse(res);
return res;
}
}
102. 二叉树的层序遍历
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) {
return res;
}
List<Integer> list = new ArrayList<>();
LinkedList<TreeNode> queue = new LinkedList<>();
queue.offer(root);
// while循环管从上到下的遍历
while(!queue.isEmpty()) {
// 注意这里不能直接写成 i < queue.size
// 因为遍历的同时也在向队列加元素,我们要确保遍历完一层,添加进结果集之后再处理新加进来的节点。
int size = queue.size();
// for循环管从左到右的遍历
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
list.add(node.val);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
res.add(list);
list = new ArrayList<>();
}
return res;
}
}
95. 不同的二叉搜索树 II⭐⭐⭐
给你一个整数 n ,请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。

输入:n = 3
输出:[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]
class Solution {
public List<TreeNode> generateTrees(int n) {
return build(1, n);
}
private List<TreeNode> build(int start, int end) {
List<TreeNode> ans = new ArrayList<>();
// 此时没有数字,将 null 加入结果中。
if (start > end) {
ans.add(null);
return ans;
}
// 我觉得这个题非常像构造树的那一类题,这个题是题目已经告诉了节点的值是1-n。
// 尝试每个数字作为根节点。
for (int i = start; i <= end; i++) {
// 得到所有可能的左子树
List<TreeNode> leftTrees = build(start, i - 1);
// 得到所有可能的右子树
List<TreeNode> rightTrees = build(i + 1, end);
// 左子树右子树两两组合
for (TreeNode leftTree : leftTrees) {
for (TreeNode rightTree : rightTrees) {
TreeNode root = new TreeNode(i, leftTree, rightTree);
// 加入到最终结果中
ans.add(root);
}
}
}
return ans;
}
}
96. 不同的二叉搜索树⭐⭐⭐
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
1、首先,我们要知道二叉搜索树的性质,对于一个二叉搜索树,其 【左边的节点值 < 中间的节点值 < 右边的节点值】,也就是说,对于一个二叉搜索树,其中序
遍历之后形成的数组应该是一个递增的序列,如下图:
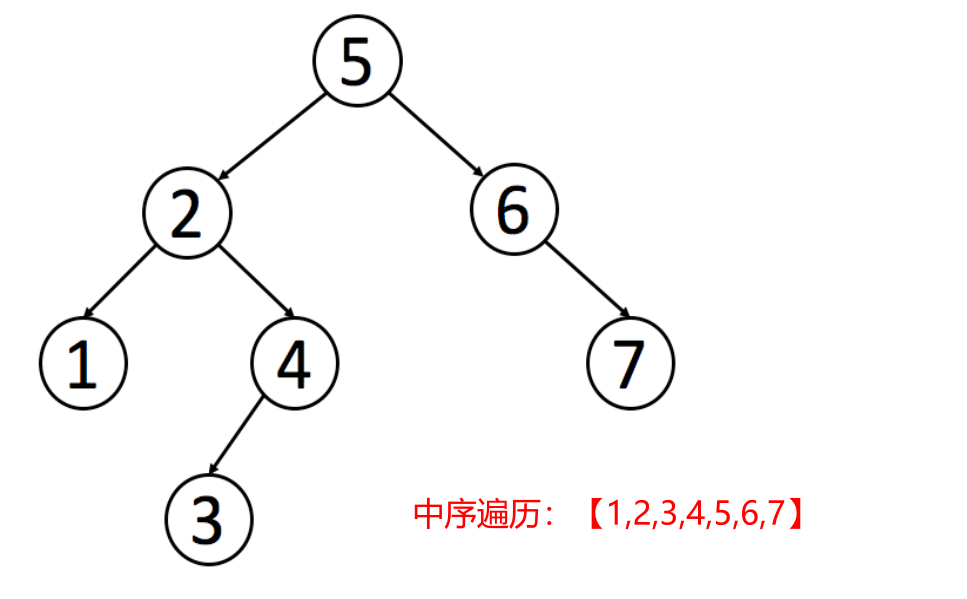
2、我们不妨就假设我们拿到了一个中序遍历的数组nums = [1,2,3,4,5,6,7],来思考一个这样的数组能延伸出多少种二叉搜索树;
3、首先,对于数组中的每一个元素,都有可能成为二叉树最顶部的root节点,例如上图中,是nums[4]这个值,即5,充当了root节点;
4、还拿5这个节点为例,即上图,其左边有四个节点,右边有两个节点。对于左边的四个节点,假设能延伸出 n 种二叉搜索树子树,对于右边的两个节点,假设
能延伸出 m 种二叉搜索树子树。则以5为root节点时的二叉搜索树总数为 m*n;
5、这样我们遍历刚刚的nums数组以值i(注意不是下标)当做根节点,其左边有i-1个节点,右边有n-i个节点,计算出可能的二叉搜索树数量,添加到总结果里。
这道题目是记忆化递归,按理说应该可以用动态规划来做。从定义上来讲,空节点也是一棵二叉树,也是一棵二叉搜索树,这是可以说得通的。
class Solution {
Map<Integer, Integer> map = new HashMap<>();
public int numTrees(int n) {
// 如果只有0,或者1个节点,则可能的子树情况为1种。
if (n == 0 || n == 1) {
return 1;
}
// 如果之前已经算过可以n个数可以构成的二叉搜索树的数量,直接取,不要重复计算。
if (map.containsKey(n)) {
return map.get(n);
}
int count = 0;
for (int i = 1; i <= n; i++) {
// 当用i这个节点当做根节点时
// 左边有多少种子树
int leftNum = numTrees(i - 1);
// 右边有多少种子树
int rightNum = numTrees(n - i);
// 乘起来就是当前节点的子树个数
count += leftNum * rightNum;
}
// 将这一轮计算的n可以组成多少种二叉搜索树放入map种。
map.put(n, count);
return count;
}
}
104. 二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
class Solution {
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int ans = 0;
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
// for循环结束一次说明遍历完一层,高度加1。
ans++;
}
return ans;
}
}
// 遍历思路
class Solution {
// 记录最大深度
int res = 0;
// 记录遍历到的节点的深度
int depth = 0;
// 主函数
int maxDepth(TreeNode root) {
traverse(root);
return res;
}
// 二叉树遍历框架
void traverse(TreeNode root) {
if (root == null) {
return;
}
// 前序位置
depth++;
if (root.left == null && root.right == null) {
// 到达叶子节点,更新最大深度
res = Math.max(res, depth);
}
traverse(root.left);
traverse(root.right);
// 后序位置
depth--;
}
}
// 分解问题思路
class Solution {
// 定义:输入根节点,返回这棵二叉树的最大深度。
int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
// 利用定义,计算左右子树的最大深度。
int leftMax = maxDepth(root.left);
int rightMax = maxDepth(root.right);
// 整棵树的最大深度等于左右子树的最大深度取最大值。
// 然后再加上根节点自己。
int res = Math.max(leftMax, rightMax) + 1;
return res;
}
}
114. 二叉树展开为链表⭐⭐
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。
- 展开后的单链表应该与二叉树 先序遍历 顺序相同。
// 遍历解法
class Solution {
public void flatten(TreeNode root) {
List<TreeNode> list = new ArrayList<>();
//获取二叉树前序遍历的节点
preorderTraversal(root, list);
//如果二叉树是空,直接返回
if (list.size() == 0) {
return;
}
//重新构造二叉树
TreeNode parent = root;
for (int i = 1; i < list.size(); i++) {
// 从1位置开始获取节点,因为0位置就是root节点。
parent.right = list.get(i);
parent.left = null;//左子节点为空
parent = parent.right;
}
}
//通过前序遍历获取二叉树的节点
public void preorderTraversal(TreeNode root, List<TreeNode> list) {
if (root == null) {
return;
}
list.add(root);
preorderTraversal(root.left, list);//递归左子节点
preorderTraversal(root.right, list);//递归右子节点
}
}
这里再看一种分解问题的解法
我们尝试给出 flatten 函数的定义:
// 定义:输入节点 root,然后 root 为根的二叉树就会被拉平为一条链表
void flatten(TreeNode root);
有了这个函数定义,如何按题目要求把一棵树拉平成一条链表?
对于一个节点 x,可以执行以下流程:
1、先利用 flatten(x.left) 和 flatten(x.right) 将 x 的左右子树拉平。
2、将 x 的右子树接到左子树下方,然后将整个左子树作为右子树。

这样,以 x 为根的整棵二叉树就被拉平了,恰好完成了 flatten(x) 的定义。
直接看代码实现:
class Solution {
// 将以root为根节点的二叉树拉平为链表
public void flatten(TreeNode root) {
if (root == null) {
return;
}
// 将左右子树都拉平为链表
flatten(root.left);
flatten(root.right);
TreeNode left = root.left;
TreeNode right = root.right;
root.left = null;
root.right = left;
TreeNode cur = root;
while (cur.right != null) {
cur = cur.right;
}
cur.right = right;
}
}
你看,这就是递归的魅力,你说 flatten 函数是怎么把左右子树拉平的?
不容易说清楚,但是只要知道 flatten 的定义如此并利用这个定义,让每一个节点做它该做的事情,然后 flatten 函数就会按照定义工作。
二叉树解题的思维模式分两类:
1、是否可以通过遍历一遍二叉树得到答案?如果可以,用一个 traverse 函数配合外部变量来实现,这叫「遍历」的思维模式。
2、是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案?
如果可以,写出这个递归函数的定义,并充分利用这个函数的返回值,这叫「分解问题」的思维模式。
无论使用哪种思维模式,你都需要思考:
如果单独抽出一个二叉树节点,它需要做什么事情?需要在什么时候(前/中/后序位置)做其他的节点不用你操心递归函数会帮你在所有节点上执行相同的操作。
希望你能仔细体会,并运用到所有二叉树题目上。
二叉搜索树展开为有序链表
我们尝试给出 flatten 函数的定义:
// 定义:输入节点 root,然后 root 为根的二叉树就会被拉平为一条链表,并且返回有序链表的头节点。
TreeNode flatten(TreeNode root);
有了这个函数定义,如何按题目要求把一棵树拉平成一条有序链表?
class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
}
public TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
// 分解问题的思路
class Solution {
public TreeNode flatten(TreeNode root) {
if (root == null) {
return null;
}
TreeNode leftTree = flatten(root.left);
TreeNode rightTree = flatten(root.right);
root.left = null;
root.right = null;
if (leftTree != null) {
TreeNode cur = leftTree;
while (cur.right != null) {
cur = cur.right;
}
cur.right = root;
root.right = rightTree;
} else {
root.right = rightTree;
return root;
}
return leftTree;
}
}
class Main {
public static void main(String[] args) {
TreeNode root = parseTreeNode(new Integer[]{5, 3, 7, 2, 4, 6, 8});
TreeNode flatten = new Solution().flatten(root);
while (flatten.right != null) {
System.out.print(flatten.val + " ");
flatten = flatten.right;
}
}
private static TreeNode parseTreeNode(Integer[] values) {
TreeNode root = null;
java.util.LinkedList<TreeNode> nodes = new java.util.LinkedList<>();
int i = 0;
while (i < values.length) {
if (i == 0) {
root = new TreeNode(values[i]);
i += 1;
nodes.addLast(root);
continue;
}
TreeNode parent = nodes.pop();
if (values[i] != null) {
TreeNode left = new TreeNode(values[i]);
parent.left = left;
nodes.addLast(left);
}
if (i + 1 < values.length && values[i + 1] != null) {
TreeNode right = new TreeNode(values[i + 1]);
parent.right = right;
nodes.addLast(right);
}
i += 2;
}
return root;
}
}
// 遍历的思路
class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
}
public TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
class Solution {
public TreeNode flatten(TreeNode root) {
List<TreeNode> list = new ArrayList<>();
inorderTraversal(root, list);
if (list.size() == 0) {
return null;
}
//重新构造二叉树
TreeNode parent = list.get(0);
TreeNode cur = parent;
for (int i = 1; i < list.size(); i++) {
// 从1位置开始获取节点,因为0位置就是root节点。
cur.right = list.get(i);
cur.left = null;//左子节点为空
cur = cur.right;
}
return parent;
}
//通过前序遍历获取二叉树的节点
public void inorderTraversal(TreeNode root, List<TreeNode> list) {
if (root == null) {
return;
}
inorderTraversal(root.left, list);//递归左子节点
list.add(root);
inorderTraversal(root.right, list);//递归右子节点
}
}
class Main {
public static void main(String[] args) {
TreeNode root = parseTreeNode(new Integer[]{5, 3, 7, 2, 4, 6, 8});
TreeNode parent = new Solution().flatten(root);
while (parent.right != null) {
System.out.print(parent.val + " ");
parent = parent.right;
}
}
private static TreeNode parseTreeNode(Integer[] values) {
TreeNode root = null;
java.util.LinkedList<TreeNode> nodes = new java.util.LinkedList<>();
int i = 0;
while (i < values.length) {
if (i == 0) {
root = new TreeNode(values[i]);
i += 1;
nodes.addLast(root);
continue;
}
TreeNode parent = nodes.pop();
if (values[i] != null) {
TreeNode left = new TreeNode(values[i]);
parent.left = left;
nodes.addLast(left);
}
if (i + 1 < values.length && values[i + 1] != null) {
TreeNode right = new TreeNode(values[i + 1]);
parent.right = right;
nodes.addLast(right);
}
i += 2;
}
return root;
}
}
111. 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
// BFS写法
class Solution {
public int minDepth(TreeNode root) {
if (root == null) {
return 0;
}
int level = 0;
LinkedList<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
// 注意层数加的位置和二叉树最大深度位置不一样。
// 求二叉树最大深度是把每一层都遍历完了,再加层数。
level++;
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
// 如果检测到当前层的某一个节点的左右孩子均为null,直接返回答案。
if (node.left == null && node.right == null) {
return level;
}
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}
return 0;
}
}
// 递归写法
class Solution {
public int minDepth(TreeNode root) {
if (root == null) return 0;
//这道题递归条件里分为三种情况
//1.左孩子和有孩子都为空的情况,说明到达了叶子节点,直接返回1即可。
if (root.left == null && root.right == null) {
return 1;
}
//2.如果左孩子和由孩子其中一个为空,那么需要返回比较大的那个孩子的深度。
int m1 = minDepth(root.left);
int m2 = minDepth(root.right);
//这里其中一个节点为空,说明m1和m2有一个必然为0,所以可以返回m1 + m2 + 1;
if (root.left == null || root.right == null) {
return m1 + m2 + 1;
}
//3.最后一种情况,也就是左右孩子都不为空,返回最小深度+1即可
return Math.min(m1, m2) + 1;
}
}
116. 填充每个节点的下一个右侧节点指针
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node left;
Node right;
Node next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
// 迭代解法。将每层倒数第二个节点的next指向每层最后一个节点。
class Solution {
public Node connect(Node root) {
if (root == null) {
return root;
}
LinkedList<Node> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
Node node = queue.poll();
if (i < size - 1) {
node.next = queue.peek();
}
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}
return root;
}
}
// 递归解法
class Solution {
// 主函数
public Node connect(Node root) {
if (root == null) return null;
// 遍历「三叉树」,连接相邻节点
traverse(root.left, root.right);
return root;
}
// 三叉树遍历框架
void traverse(Node node1, Node node2) {
if (node1 == null || node2 == null) {
return;
}
/**** 前序位置 ****/
// 将传入的两个节点穿起来
node1.next = node2;
// 连接相同父节点的两个子节点
traverse(node1.left, node1.right);
traverse(node2.left, node2.right);
// 连接跨越父节点的两个子节点
traverse(node1.right, node2.left);
}
}
剑指 Offer 32 - III. 从上到下打印二叉树 III
请实现一个函数按照之字形顺序打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右到左的顺序打印,第三行再按照从左到右的顺序打印,其他行以
此类推。
其实就是层序遍历,只不过不同层加入集合的方式不一样。
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) {
return res;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int row = 1;
while (!queue.isEmpty()) {
LinkedList<Integer> list = new LinkedList<>();
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
if ((row & 1) == 1) {
// 这是一般我们使用队列的添加方式从右边尾部入队
list.addLast(node.val); // 从队列的尾部加入元素,最终这一层的结果集就是从左到右。
} else {
list.addFirst(node.val); // 从队列的头部加入元素,最终这一层的结果集就是从右到左。
}
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
// 遍历完一行,行数加一。
row++;
res.add(list);
}
return res;
}
}
222. 完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,
则该层包含 1~ 2^h 个节点。
如果用遍历的方式时间复杂度是O(n)。
class Solution {
public int countNodes(TreeNode root) {
TreeNode l = root, r = root;
// 沿最左侧和最右侧分别计算高度
int hl = 0, hr = 0;
while (l != null) {
l = l.left;
hl++;
}
while (r != null) {
r = r.right;
hr++;
}
// 如果左右侧计算的高度相同,则是一棵满二叉树
if (hl == hr) {
return (int)Math.pow(2, hl) - 1;
}
// 如果左右侧的高度不同,则按照普通二叉树的逻辑计算
return 1 + countNodes(root.left) + countNodes(root.right);
}
}
124. 二叉树中的最大路径和⭐⭐⭐😲
路径 被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。
该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
其实这道题和二叉树的直径差不多,二叉树的直径是左右深度之后最大的
class Solution {
int res = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
if (root == null) {
return 0;
}
// 计算单边路径和时顺便计算最大路径和
oneSideMax(root);
return res;
}
// 定义:计算从根节点 root 为起点的最大单边路径和。
int oneSideMax(TreeNode root) {
if (root == null) {
return 0;
}
// 这里要和0比较取大值的原因是如果左右子树返回的单边最大值是负值。
// 那我这个节点还不如不要左或者右的单边最大值。
int leftMaxSum = Math.max(0, oneSideMax(root.left));
int rightMaxSum = Math.max(0, oneSideMax(root.right));
// 后序遍历位置,顺便更新最大路径和
int pathMaxSum = root.val + leftMaxSum + rightMaxSum;
res = Math.max(res, pathMaxSum);
// 实现函数定义,左右子树的最大单边路径和加上根节点的值
// 就是从根节点 root 为起点的最大单边路径和
return Math.max(leftMaxSum, rightMaxSum) + root.val;
}
}
129. 求根节点到叶节点数字之和
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
- 例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。

输入:root = [1,2,3]
输出:25
解释:
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此,数字总和 = 12 + 13 = 25
// 层序遍历写法
class Solution {
// 用map来存放当前遍历到的节点以及父节点的映射。
Map<TreeNode, TreeNode> map = new HashMap<>();
public int sumNumbers(TreeNode root) {
int sum = 0;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
// 到叶子节点
if (node.left == null && node.right == null) {
sum += Integer.parseInt(builder(node));
}
if (node.left != null) {
queue.offer(node.left);
map.put(node.left, node);
}
if (node.right != null) {
queue.offer(node.right);
map.put(node.right, node);
}
}
return sum;
}
public String builder(TreeNode node) {
StringBuilder sb = new StringBuilder();
while (node != null) {
sb.append(node.val);
node = map.get(node);
}
// 字符串反转就行相加
return sb.reverse().toString();
}
}
class Solution {
StringBuilder path = new StringBuilder();
int res = 0;
public int sumNumbers(TreeNode root) {
// 遍历一遍二叉树就能出结果
traverse(root);
return res;
}
// 二叉树遍历函数
void traverse(TreeNode root) {
if (root == null) {
return;
}
// 前序遍历位置,记录节点值
path.append(root.val);
if (root.left == null && root.right == null) {
// 到达叶子节点,累加路径和
res += Integer.parseInt(path.toString());
}
// 二叉树递归框架,遍历左右子树
traverse(root.left);
traverse(root.right);
// 后续遍历位置,撤销节点值
path.deleteCharAt(path.length() - 1);
}
}
226. 翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
通过遍历解决:
// 层序遍历的迭代写法,我曾经的最爱!嘻嘻嘻,无语了。
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
LinkedList<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
// 这一层的节点数
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
// 交换节点的左右子树
swapNode(node);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}
return root;
}
public void swapNode(TreeNode root) {
TreeNode tempNode = root.left;
root.left = root.right;
root.right = tempNode;
}
}
// 遍历思路
class Solution {
// 主函数
TreeNode invertTree(TreeNode root) {
// 遍历二叉树,交换每个节点的子节点
traverse(root);
return root;
}
// 二叉树遍历函数
void traverse(TreeNode root) {
if (root == null) {
return;
}
/**** 前序位置 ****/
// 每一个节点需要做的事就是交换它的左右子节点
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
// 遍历框架,去遍历左右子树的节点
traverse(root.left);
traverse(root.right);
}
}
// 分解问题思路
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
TreeNode left = invertTree(root.left);
TreeNode right = invertTree(root.right);
root.left = right;
root.right = left;
return root;
}
}
235. 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也
可以是它自己的祖先)。”
/**
* 由于这道题是求二叉搜索树中两个节点的最近公共祖先,
* 根据二叉搜索树的特性,当根节点的值大于两个节点的值时,那么应该在左子树上去找,
* 当根节点的值小于两个节点的值时,此时就应该去右子树上去找。
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
while (true) {
// 去左子树上找
if (root.val > p.val && root.val > q.val) {
root = root.left;
// 去右子树上找
} else if (root.val < p.val && root.val < q.val) {
root = root.right;
} else {
break;
}
}
return root;
}
}
236. 二叉树的最近公共祖先⭐
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也
可以是它自己的祖先)。”
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// 记录遍历到的每个节点的父节点。
Map<TreeNode, TreeNode> parent = new HashMap<>();
Queue<TreeNode> queue = new LinkedList<>();
// 根节点没有父节点,所以为空。
parent.put(root, null);
queue.add(root);
// 直到两个节点都找到为止。
while (!parent.containsKey(p) || !parent.containsKey(q)) {
// 队列是一边进一边出,这里poll方法是出队。
TreeNode node = queue.poll();
if (node.left != null) {
// 左子节点不为空,记录下他的父节点。
parent.put(node.left, node); // 显然node是node.left的父节点。
// 左子节点不为空,把它加入到队列中。
queue.add(node.left);
}
// 右节点同上
if (node.right != null) {
parent.put(node.right, node);
queue.add(node.right);
}
}
Set<TreeNode> ancestors = new HashSet<>();
// 记录下p和他的祖先节点,从p节点开始一直到根节点。
while (p != null) {
ancestors.add(p);
p = parent.get(p); // 把p的直接父节点赋值给p。
}
// 查看p和他的祖先节点是否包含q节点,如果不包含再看是否包含q的父节点。
while (!ancestors.contains(q)) {
q = parent.get(q);
}
return q;
}
}
寻找一个元素:
先不管最近公共祖先问题,我请你实现一个简单的算法:
给你输入一棵没有重复元素的二叉树根节点 root 和一个目标值 val,请你写一个函数寻找树中值为 val 的节点。
函数签名如下:
TreeNode find(TreeNode root, int val);
这个函数应该很容易实现对吧,比如我这样写代码:
// 定义:在以 root 为根的二叉树中寻找值为 val 的节点
TreeNode find(TreeNode root, int val) {
// base case
if (root == null) {
return null;
}
// 看看 root.val 是不是要找的
if (root.val == val) {
return root;
}
// root 不是目标节点,那就去左子树找
TreeNode left = find(root.left, val);
if (left != null) {
return left;
}
// 左子树找不着,那就去右子树找
TreeNode right = find(root.right, val);
if (right != null) {
return right;
}
// 实在找不到了
return null;
}
这段代码应该不用我多解释了,我下面基于这段代码做一些简单的改写,请你分析一下我的改动会造成什么影响。
首先,我修改一下 return 的位置:
TreeNode find(TreeNode root, int val) {
if (root == null) {
return null;
}
// 前序位置
if (root.val == val) {
return root;
}
// root 不是目标节点,去左右子树寻找
TreeNode left = find(root.left, val);
TreeNode right = find(root.right, val);
// 看看哪边找到了
return left != null ? left : right;
}
这段代码也可以达到目的,但是实际运行的效率会低一些,原因也很简单,如果你能够在左子树找到目标节点,还有没有必要去右子树找了?没有必要。
但这段代码还是会去右子树找一圈,所以效率相对差一些。
更进一步,我把对 root.val 的判断从前序位置移动到后序位置:
TreeNode find(TreeNode root, int val) {
if (root == null) {
return null;
}
// 先去左右子树寻找
TreeNode left = find(root.left, val);
TreeNode right = find(root.right, val);
// 后序位置,看看 root 是不是目标节点
if (root.val == val) {
return root;
}
// root 不是目标节点,再去看看哪边的子树找到了
return left != null ? left : right;
}
这段代码相当于你先去左右子树找,然后才检查 root,依然可以到达目的,但是效率会进一步下降。因为这种写法必然会遍历二叉树的每一个节点。
对于之前的解法,你在前序位置就检查 root,如果输入的二叉树根节点的值恰好就是目标值 val,那么函数直接结束了,其他的节点根本不用搜索。
但如果你在后序位置判断,那么就算根节点就是目标节点,你也要去左右子树遍历完所有节点才能判断出来。
最后,我再改一下题目,现在不让你找值为 val 的节点,而是寻找值为 val1 或 val2 的节点,函数签名如下:
TreeNode find(TreeNode root, int val1, int val2);
这和我们第一次实现的 find 函数基本上是一样的,而且你应该知道可以有多种写法,我选择这样写代码:
// 定义:在以 root 为根的二叉树中寻找值为 val1 或 val2 的节点
TreeNode find(TreeNode root, int val1, int val2) {
// base case
if (root == null) {
return null;
}
// 前序位置,看看 root 是不是目标值
if (root.val == val1 || root.val == val2) {
return root;
}
// 去左右子树寻找
TreeNode left = find(root.left, val1, val2);
TreeNode right = find(root.right, val1, val2);
// 后序位置,已经知道左右子树是否存在目标值
return left != null ? left : right;
}
为什么要写这样一个奇怪的 find 函数呢?因为最近公共祖先系列问题的解法都是把这个函数作为框架的。
下面一道一道题目来看。
先来看看力扣第 236 题「二叉树的最近公共祖先」:
给你输入一棵不含重复值的二叉树,以及存在于树中的两个节点 p 和 q,请你计算 p 和 q 的最近公共祖先节点。
比如输入这样一棵二叉树:

如果 p 是节点 6,q 是节点 7,那么它俩的 LCA 就是节点 5:
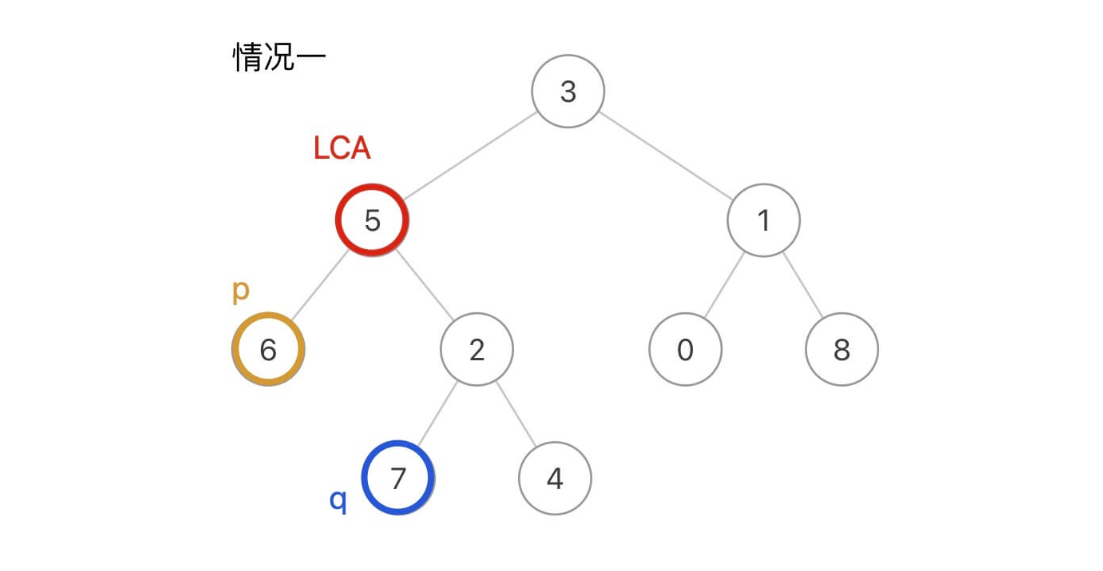
当然,p 和 q 本身也可能是 LCA,比如这种情况 q 本身就是 LCA 节点:
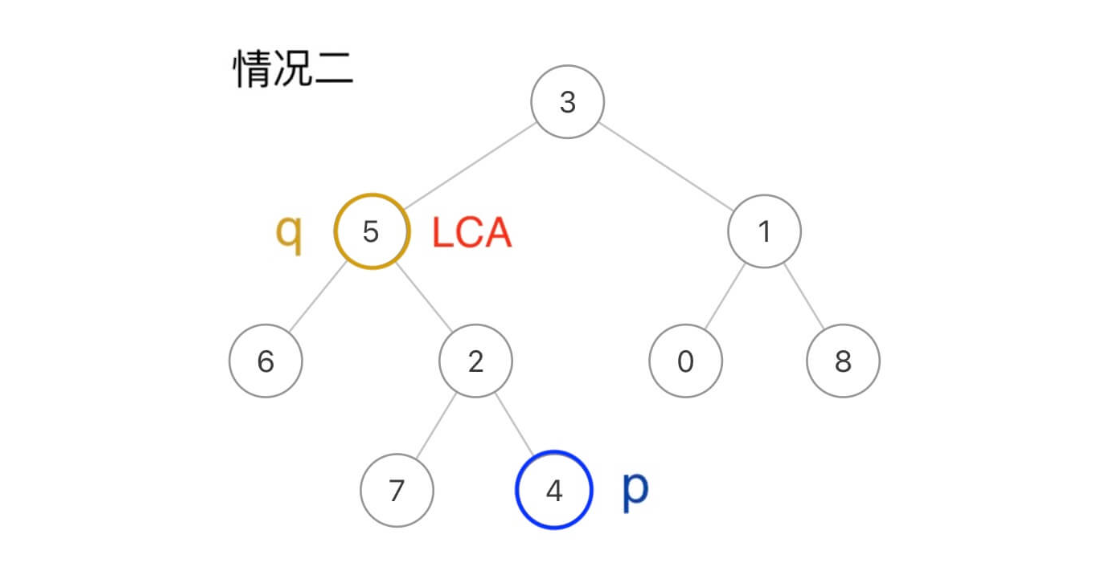
两个节点的最近公共祖先其实就是这两个节点向根节点的「延长线」的交汇点,那么对于任意一个节点,它怎么才能知道自己是不是 p 和 q 的最近公共祖先?
如果一个节点能够在它的左右子树中分别找到 p 和 q,则该节点为 LCA 节点。
这就要用到之前实现的 find 函数了,只需在后序位置添加一个判断逻辑,即可改造成寻找最近公共祖先的解法代码:
TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
return find(root, p.val, q.val);
}
// 在二叉树中寻找 val1 和 val2 的最近公共祖先节点
TreeNode find(TreeNode root, int val1, int val2) {
if (root == null) {
return null;
}
// 前序位置
if (root.val == val1 || root.val == val2) {
// 如果遇到目标值,直接返回
return root;
}
TreeNode left = find(root.left, val1, val2);
TreeNode right = find(root.right, val1, val2);
// 后序位置,已经知道左右子树是否存在目标值
if (left != null && right != null) {
// 当前节点是 LCA 节点
return root;
}
return left != null ? left : right;
}
在 find 函数的后序位置,如果发现 left 和 right 都非空,就说明当前节点是 LCA 节点,即解决了第一种情况:

在 find 函数的前序位置,如果找到一个值为 val1 或 val2 的节点则直接返回,恰好解决了第二种情况:
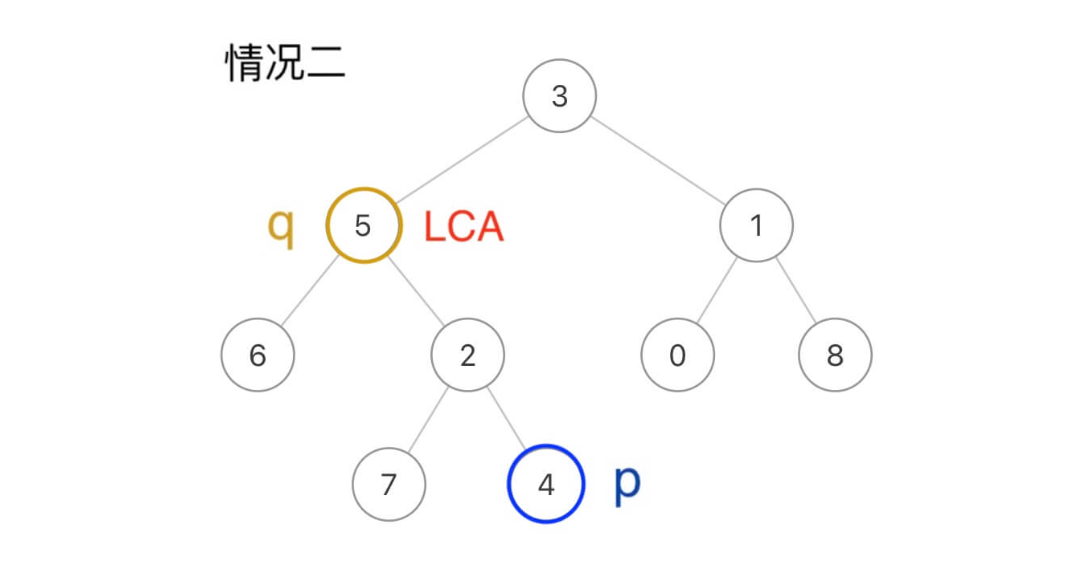
因为题目说了 p 和 q 一定存在于二叉树中(这点很重要),所以即便我们遇到 q 就直接返回,根本没遍历到 p,也依然可以断定 p 在 q 底下,q 就是 LCA 节点。
257. 二叉树的所有路径(遍历问题)
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
class Solution {
public List<String> binaryTreePaths(TreeNode root) {
// 遍历一遍二叉树就能出结果了
traverse(root);
return res;
}
// 记录 traverse 函数递归时的路径
LinkedList<String> path = new LinkedList<>();
// 记录所有从根节点到叶子节点的路径
LinkedList<String> res = new LinkedList<>();
void traverse(TreeNode root) {
if (root == null) {
return;
}
// root 是叶子节点
if (root.left == null && root.right == null) {
path.addLast(root.val + "");
// 将这条路径装入 res
res.addLast(String.join("->", path));
path.removeLast();
return;
}
// 前序遍历位置
path.addLast(root.val + "");
// 递归遍历左右子树
traverse(root.left);
traverse(root.right);
// 后序遍历位置
path.removeLast();
}
}
515. 在每个树行中找最大值
给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。
class Solution {
public static List<Integer> largestValues(TreeNode root) {
List<Integer> list = new ArrayList<>();
List<Integer> maxList = new ArrayList<>();
if (root == null) {
return maxList;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
// 记录当前一层的节点个数
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
list.add(node.val);
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
// 求出这一层的最大值
int max = 0;
for (int i = 0; i < list.size(); i++) {
if (i == 0) {
max = list.get(0);
} else {
max = Math.max(max, list.get(i));
}
}
maxList.add(max);
list.clear();
}
return maxList;
}
}
543. 二叉树的直径(分解)⭐😲
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
1 / \ 2 3 / \ 4 5
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
每一条二叉树的「直径」长度,就是一个节点的左右子树的最大深度之和。
就是说有这样的节点存在,它的左子树深度和右子树深度之和是所有节点中最大的。那么这个左右深度之和就是二叉树的直径。
/**
* 求二叉树的直径就是在求所有树节点的左右子树深度之和最大的那一个。
*
* 这题是分解问题的思想,后序位置收集到左右子树的信息。
*/
class Solution {
int diameter;
public int diameterOfBinaryTree(TreeNode root) {
diameter = 0;
traverse(root);
return diameter;
}
// 返回树的深度
int traverse(TreeNode root) {
if (root == null) {
return 0;
}
int left = traverse(root.left); // 左子树的深度
int right = traverse(root.right); // 右子树的深度
// 直接访问全局变量
// 后序遍历二叉树求每个树节点左右子树的深度,可以看出后序遍历是分解问题的思路。
// 二叉树的直径就是所有节点左右子树深度之和的最大值。
diameter = Math.max(diameter, left + right);
return Math.max(left, right) + 1;
}
}
606. 根据二叉树创建字符串(分解问题)⭐⭐
给你二叉树的根节点 root ,请你采用前序遍历的方式,将二叉树转化为一个由括号和整数组成的字符串,返回构造出的字符串。
空节点使用一对空括号对 "()" 表示,转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。
题目翻译:
题目的意思是子节点需要用()来包裹。举例来说,二叉树[root,left,right],则转换为root(left)(right)。
如果只有left为空节点,则输出root()(right),如果只有right为空节点则可以忽略右节点的(),输出为root(left)。
class Solution {
// 定义:输入以 root 的二叉树,返回描述该二叉树的字符串
public String tree2str(TreeNode root) {
// base case
if (root == null) return "";
if (root.left == null && root.right == null) {
return root.val + "";
}
// 递归生成左右子树的字符串
String leftStr = tree2str(root.left);
String rightStr = tree2str(root.right);
// 后序遍历代码位置
// 根据左右子树字符串组装出前序遍历的顺序
// 按题目要求处理 root 只有一边有子树的情况
if (root.left != null && root.right == null) {
// 省略空的右子树
return root.val + "(" + leftStr + ")";
}
if (root.left == null && root.right != null) {
// 空的左子树不能省略
return root.val + "()" + "(" + rightStr + ")";
}
// 按题目要求处理 root 左右子树都不空的情况
return root.val + "(" + leftStr + ")" + "(" + rightStr + ")";
}
}
669. 修剪二叉搜索树(分解问题)⭐⭐⭐
给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。
修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。

输入:root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出:[3,2,null,1]
// 你希望一个节点做什么就怎么写,其余交给递归去做。
class Solution {
// 定义:删除 BST 中小于 low 和大于 high 的所有节点,返回结果 BST。
public TreeNode trimBST(TreeNode root, int low, int high) {
if (root == null) {
return null;
}
if (root.val < low) {
// 直接返回 root.right
// 等于删除 root 以及 root 的左子树
return trimBST(root.right, low, high);
}
if (root.val > high) {
// 直接返回 root.left
// 等于删除 root 以及 root 的右子树
return trimBST(root.left, low, high);
}
// 闭区间 [lo, hi] 内的节点什么都不做,递归调用函数修剪二叉搜索树。
root.left = trimBST(root.left, low, high);
root.right = trimBST(root.right, low, high);
return root;
}
}
654. 最大二叉树(分解问题)⭐⭐⭐
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
- 创建一个根节点,其值为 nums 中的最大值。
- 递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的最大二叉树 。
// 你希望一个节点做什么就怎么写代码,基于节点交给递归去处理。
class Solution {
public TreeNode constructMaximumBinaryTree(int[] nums) {
return build(nums, 0, nums.length - 1);
}
// 辅助函数,构造二叉树,返回二叉树的根节点。
public TreeNode build(int[] nums, int left, int right) {
// 递归出口
if (left > right) {
return null;
}
// 找到数组中最大的元素的位置。
int index = -1;
int maxValue = Integer.MIN_VALUE;
for (int i = left; i <= right; i++) {
if (nums[i] > maxValue) {
index = i;
maxValue = nums[i];
}
}
// 构造根节点。
TreeNode root = new TreeNode(maxValue);
// 递归调用函数构造左右子树。
root.left = build(nums, left, index - 1);
root.right = build(nums, index + 1, right);
return root;
}
}
998. 最大二叉树 II
这道题的题目描述中文翻译的非常糟糕,建议看一下英文的描述,大致意思就是:给你一个已经构造好的最大二叉树,根据654题的描述,这个最大二叉树是对应
一个数组的,现在这个数组后面append一个元素val,然后重新构造一个最大二叉树。
输入:root = [5,2,3,null,1], val = 4
输出:[5,2,4,null,1,3]
解释:a = [2,1,5,3], b = [2,1,5,3,4]
解题思路:
新增的 val 是添加在原始数组的最后的,根据构建最大二叉树的逻辑,正常来说最后的这个值一定是在右子树的,可以对右子树递归调用 insertIntoMaxTree
插入进去。但是一种特殊情况是 val 比原始数组中的所有元素都大,那么根据构建最大二叉树的逻辑,原来的这棵树应该成为 val 节点的左子树。
class Solution {
public TreeNode insertIntoMaxTree(TreeNode root, int val) {
if (root == null) {
return new TreeNode(val);
}
if (root.val < val) {
// 如果 val 是整棵树最大的,那么原来的这棵树应该是 val 节点的左子树,
// 因为 val 节点是接在原始数组 a 的最后一个元素
TreeNode temp = root;
root = new TreeNode(val);
root.left = temp;
} else {
// 如果 val 不是最大的,那么就应该在右子树上,
// 因为 val 节点是接在原始数组 a 的最后一个元素
root.right = insertIntoMaxTree(root.right, val);
}
return root;
}
}
105. 从前序与中序遍历序列构造二叉树(分解问题)⭐⭐⭐
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
List<Integer> preOrderList = new ArrayList<>();
List<Integer> inOrderList = new ArrayList<>();
for (int i = 0; i < preorder.length; i++) {
preOrderList.add(preorder[i]);
inOrderList.add(inorder[i]);
}
return helper(preOrderList, inOrderList);
}
private TreeNode helper(List<Integer> preOrderList, List<Integer> inOrderList) {
// 递归的构建子树,当一个子树的中序遍历集合为空时,返回null就行了。
if (inOrderList.size() == 0) {
return null;
}
// 这里借助List的api,当remove(int index)删掉index位置元素之后,会将index位置后面的元素向前移动一个单元。
int rootVal = preOrderList.remove(0);
TreeNode root = new TreeNode(rootVal);
// indexOf根据值找到下标。
int mid = inOrderList.indexOf(rootVal);
root.left = helper(preOrderList, inOrderList.subList(0, mid));
root.right = helper(preOrderList, inOrderList.subList(mid + 1, inOrderList.size()));
return root;
}
}
// 分解问题思路,在前序位置做处理单个节点的逻辑,然后递归处理左右子树。返回的节点再赋给root节点的左右子树。
class Solution {
// 存储 inorder 中值到索引的映射。
HashMap<Integer, Integer> valToIndex = new HashMap<>();
public TreeNode buildTree(int[] preorder, int[] inorder) {
for (int i = 0; i < inorder.length; i++) {
valToIndex.put(inorder[i], i);
}
return build(preorder, 0, preorder.length - 1,
inorder, 0, inorder.length - 1);
}
/*
定义:前序遍历数组为 preorder[preStart..preEnd],
中序遍历数组为 inorder[inStart..inEnd],
构造这个二叉树并返回该二叉树的根节点。
*/
TreeNode build(int[] preorder, int preStart, int preEnd,
int[] inorder, int inStart, int inEnd) {
if (preStart > preEnd) {
return null;
}
// root 节点对应的值就是前序遍历数组的第一个元素。
int rootVal = preorder[preStart];
// rootVal 在中序遍历数组中的索引。
int index = valToIndex.get(rootVal);
int leftSize = index - inStart;
// 先构造出当前根节点。
TreeNode root = new TreeNode(rootVal);
// 递归构造左右子树。
root.left = build(preorder, preStart + 1, (preStart + 1) + leftSize - 1,
inorder, inStart, index - 1);
root.right = build(preorder, preStart + leftSize + 1, preEnd,
inorder, index + 1, inEnd);
return root;
}
}
106. 从中序与后序遍历序列构造二叉树(分解问题)⭐⭐⭐
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树。
class Solution {
// 存储 inorder 中值到索引的映射
HashMap<Integer, Integer> valToIndex = new HashMap<>();
public TreeNode buildTree(int[] inorder, int[] postorder) {
for (int i = 0; i < inorder.length; i++) {
valToIndex.put(inorder[i], i);
}
return build(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1);
}
/*
定义:
中序遍历数组为 inorder[inStart..inEnd],
后序遍历数组为 postorder[postStart..postEnd],
构造这个二叉树并返回该二叉树的根节点
*/
TreeNode build(int[] inorder, int inStart, int inEnd, int[] postorder, int postStart, int postEnd) {
// 这个递归出口也很好理解当
if (inStart > inEnd) {
return null;
}
// root 节点对应的值就是后序遍历数组的最后一个元素
int rootVal = postorder[postEnd];
// rootVal 在中序遍历数组中的索引
int index = valToIndex.get(rootVal);
// 左子树的节点个数
int leftSize = index - inStart;
TreeNode root = new TreeNode(rootVal);
// 递归构造左右子树
root.left = build(inorder, inStart, index - 1, postorder, postStart, postStart + leftSize - 1);
root.right = build(inorder, index + 1, inEnd, postorder, postStart + leftSize, postEnd - 1);
return root;
}
}
889. 根据前序和后序遍历构造二叉树(分解问题)⭐⭐⭐
给定两个整数数组,preorder 和 postorder ,其中 preorder 是一个具有 无重复 值的二叉树的前序遍历,postorder 是同一棵树的后序遍历,重构并返回二
叉树。如果存在多个答案,您可以返回其中 任何 一个。
只有每个节点度为2或者0的时候前序和后序才能唯一确定一颗二叉树,只有一个子节点是无法确定的,因为你无法判断他是左子树还是右子树。
题目也说了,如果有多种可能的还原结果,你可以返回任意一种。
为什么呢?我们说过,构建二叉树的套路很简单,先找到根节点,然后找到并递归构造左右子树即可。
前两道题,可以通过前序或者后序遍历结果找到根节点,然后根据中序遍历结果确定左右子树(题目说了树中没有 val 相同的节点)。
这道题,你可以确定根节点,但是无法确切的知道左右子树有哪些节点。
举个例子,比如给你这个输入:
preorder = [1,2,3], postorder = [3,2,1]
下面这两棵树都是符合条件的,但显然它们的结构不同:

不过话说回来,用后序遍历和前序遍历结果还原二叉树,解法逻辑上和前两道题差别不大,也是通过控制左右子树的索引来构建:
1、首先把前序遍历结果的第一个元素或者后序遍历结果的最后一个元素确定为根节点的值。
2、然后把前序遍历结果的第二个元素作为左子树的根节点的值。
3、在后序遍历结果中寻找左子树根节点的值,从而确定了左子树的索引边界,进而确定右子树的索引边界,递归构造左右子树即可。

class Solution {
HashMap<Integer, Integer> valToIndex = new HashMap<>();
public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
for (int i = 0; i < postorder.length; i++) {
valToIndex.put(postorder[i], i);
}
return build(preorder, 0, preorder.length - 1, postorder, 0, postorder.length - 1);
}
private TreeNode build(int[] preorder, int preStart, int preEnd, int[] postorder, int postStart, int postEnd) {
if (preStart > preEnd) {
return null;
}
// 一定要注意这里,当前序遍历只剩下一个值时,直接建立节点返回了。
// 此时已经说明没有左右子树了,如果再按照下面代码执行就会出错。
if (preStart == preEnd) {
return new TreeNode(preorder[preStart]);
}
int val = preorder[preStart];
int leftVal = preorder[preStart + 1];
int leftIndex = valToIndex.get(leftVal);
int leftSize = leftIndex - postStart + 1;
TreeNode root = new TreeNode(val);
root.left = build(preorder, preStart + 1, preStart + leftSize, postorder, postStart, leftIndex);
root.right = build(preorder, preStart + leftSize + 1, preEnd, postorder, leftIndex + 1, postEnd - 1);
return root;
}
}
1008. 前序遍历构造二叉搜索树(分解问题)⭐⭐⭐
给定一个整数数组,它表示BST(即 二叉搜索树 )的 先序遍历 ,构造树并返回其根。
保证 对于给定的测试用例,总是有可能找到具有给定需求的二叉搜索树。
二叉搜索树 是一棵二叉树,其中每个节点, Node.left 的任何后代的值 严格小于 Node.val , Node.right 的任何后代的值 严格大于 Node.val。
二叉树的 前序遍历 首先显示节点的值,然后遍历Node.left,最后遍历Node.right。
解题思路:
生成二叉树的题目,无非就是先生成根节点,然后递归生成左右子树,最后把根节点和左右子树连接起来。具体区别在于你如何找到根节点,如何划分左右子树。
根据前序遍历的特点是,根节点在第一位,后面接着左子树和右子树;
BST 的特点,左子树都比根节点的值小,右子树都比根节点的值大。
所以如何找到根节点?前序遍历的第一个就是根节点。
如何找到左右子树?比根节点小的就是左子树的节点,比根节点大的就是右子树的节点。
最后,确定清楚 build 函数的定义,利用这个函数递归生成 BST 即可。
class Solution {
public TreeNode bstFromPreorder(int[] preorder) {
return build(preorder, 0, preorder.length - 1);
}
// 定义:将 preorder[start..end] 区间内的元素生成 BST,并返回根节点
private TreeNode build(int[] preorder, int start, int end) {
if (start > end) {
return null;
}
// 根据前序遍历的特点,根节点在第一位,后面接着左子树和右子树
int rootVal = preorder[start];
TreeNode root = new TreeNode(rootVal);
// 根据 BST 的特点,左子树都比根节点的值小,右子树都比根节点的值大
// p 就是左右子树的分界点
int p = start + 1;
while (p <= end && preorder[p] < rootVal) {
p++;
}
// [start+1, p-1] 区间内是左子树元素
root.left = build(preorder, start + 1, p - 1);
// [p, end] 区间内是右子树元素
root.right = build(preorder, p, end);
return root;
}
}
序列化篇
对二叉树同时进行「序列化」和「反序列化」。要说序列化和反序列化,得先从 JSON 数据格式说起。
JSON 的运用非常广泛,比如我们经常将变成语言中的结构体序列化成 JSON 字符串,存入缓存或者通过网络发送给远端服务,消费者接受 JSON 字符串然后进行
反序列化,就可以得到原始数据了。这就是序列化和反序列化的目的,以某种特定格式组织数据,使得数据可以独立于编程语言。
前序遍历写法⭐⭐
class Codec {
String SEP = ",";
String NULL = "#";
StringBuilder sb = new StringBuilder();
public String serialize(TreeNode root) {
traverse(root);
return sb.toString();
}
private void traverse(TreeNode root) {
if (root == null) {
sb.append(NULL).append(SEP);
return;
}
sb.append(root.val).append(SEP);
traverse(root.left);
traverse(root.right);
}
public TreeNode deserialize(String data) {
List<String> arr = new ArrayList<>();
String[] nodes = data.split(SEP);
for (String node : nodes) {
arr.add(node);
}
return build(arr);
}
// 可能会有一个疑问的地方就是,为什么这里只需要前序遍历就可以构造一棵二叉树了
// 因为序列化的结果是包含null节点的,而之前通过前序中序遍历构造二叉树时不知道哪些位置有null节点。
// 这是个值得思考的地方。
private TreeNode build(List<String> arr) {
if (arr.isEmpty()) {
return null;
}
String val = arr.remove(0);
if (val.equals(NULL)) {
return null;
}
TreeNode root = new TreeNode(Integer.parseInt(val));
root.left = build(arr);
root.right = build(arr);
return root;
}
}
后序遍历写法
class Codec {
String SEP = ",";
String NULL = "#";
StringBuilder sb = new StringBuilder();
public String serialize(TreeNode root) {
traverse(root);
return sb.toString();
}
private void traverse(TreeNode root) {
if (root == null) {
sb.append(NULL).append(SEP);
return;
}
traverse(root.left);
traverse(root.right);
sb.append(root.val).append(SEP);
}
public TreeNode deserialize(String data) {
LinkedList<String> arr = new LinkedList<>();
String[] nodes = data.split(SEP);
for (String node : nodes) {
arr.add(node);
}
return build(arr);
}
private TreeNode build(LinkedList<String> arr) {
if (arr.isEmpty()) {
return null;
}
String val = arr.removeLast();
if (val.equals(NULL)) {
return null;
}
TreeNode root = new TreeNode(Integer.parseInt(val));
// 先构造右子树,后构造左子树
root.right = build(arr);
root.left = build(arr);
return root;
}
}
层序遍历写法
首先,先写出层级遍历二叉树的代码框架:
void traverse(TreeNode root) {
if (root == null) return;
// 初始化队列,将 root 加入队列
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
while (!q.isEmpty()) {
TreeNode cur = q.poll();
/* 层级遍历代码位置 */
System.out.println(root.val);
/*****************/
if (cur.left != null) {
q.offer(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
}
上述代码是标准的二叉树层级遍历框架,从上到下,从左到右打印每一层二叉树节点的值,可以看到,队列 q 中不会存在 null 指针。
不过我们在反序列化的过程中是需要记录空指针 null 的,所以可以把标准的层级遍历框架略作修改:
void traverse(TreeNode root) {
if (root == null) return;
// 初始化队列,将 root 加入队列
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
while (!q.isEmpty()) {
TreeNode cur = q.poll();
/* 层级遍历代码位置 */
if (cur == null) continue;
System.out.println(root.val);
/*****************/
q.offer(cur.left);
q.offer(cur.right);
}
}
这样也可以完成层级遍历,只不过我们把对空指针的检验从「将元素加入队列」的时候改成了「从队列取出元素」的时候。
那么我们完全仿照这个框架即可写出序列化方法:
String SEP = ",";
String NULL = "#";
/* 将二叉树序列化为字符串 */
String serialize(TreeNode root) {
if (root == null) return "";
StringBuilder sb = new StringBuilder();
// 初始化队列,将 root 加入队列
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
while (!q.isEmpty()) {
TreeNode cur = q.poll();
/* 层级遍历代码位置 */
if (cur == null) {
sb.append(NULL).append(SEP);
continue;
}
sb.append(cur.val).append(SEP);
/*****************/
q.offer(cur.left);
q.offer(cur.right);
}
return sb.toString();
}
层级遍历序列化得出的结果如下图:

可以看到,每一个非空节点都会对应两个子节点,那么反序列化的思路也是用队列进行层级遍历,同时用索引 i 记录对应子节点的位置:
/* 将字符串反序列化为二叉树结构 */
TreeNode deserialize(String data) {
if (data.isEmpty()) return null;
String[] nodes = data.split(SEP);
// 第一个元素就是 root 的值
TreeNode root = new TreeNode(Integer.parseInt(nodes[0]));
// 队列 q 记录父节点,将 root 加入队列
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
for (int i = 1; i < nodes.length; ) {
// 队列中存的都是父节点
TreeNode parent = q.poll();
// 父节点对应的左侧子节点的值
String left = nodes[i++];
if (!left.equals(NULL)) {
parent.left = new TreeNode(Integer.parseInt(left));
q.offer(parent.left);
} else {
parent.left = null;
}
// 父节点对应的右侧子节点的值
String right = nodes[i++];
if (!right.equals(NULL)) {
parent.right = new TreeNode(Integer.parseInt(right));
q.offer(parent.right);
} else {
parent.right = null;
}
}
return root;
}
这段代码可以考验一下你的框架思维。仔细看一看 for 循环部分的代码,发现这不就是标准层级遍历的代码衍生出来的嘛:
while (!q.isEmpty()) {
TreeNode cur = q.poll();
if (cur.left != null) {
q.offer(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
只不过,标准的层级遍历在操作二叉树节点 TreeNode,而我们的函数在操作 nodes[i],这也恰恰是反序列化的目的嘛。
到这里,我们对于二叉树的序列化和反序列化的几种方法就全部讲完了。
652. 寻找重复的子树(借助序列化)⭐⭐
给定一棵二叉树 root,返回所有重复的子树。
对于同一类的重复子树,你只需要返回其中任意一棵的根结点即可。
如果两棵树具有相同的结构和相同的结点值,则它们是重复的。
class Solution {
Map<String, Integer> tree = new HashMap();
List<TreeNode> answer = new LinkedList<>();
public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
traverse(root);
return answer;
}
// 返回序列化子树
private String traverse(TreeNode root) {
if (root == null) {
return "#";
}
//得到序列化后的左子树
String leftTree = traverse(root.left);
//得到序列化后的右子树
String rightTree = traverse(root.right);
//后序遍历-自底向上地构建序列化子树-不断比较返回的子树是否已经存在
String treeSub = root.val + "," + leftTree + "," + rightTree;
int count = tree.getOrDefault(treeSub, 0);
//如果存在该子树
if (count == 1) {
//将该子树根节点存入结果集
answer.add(root);
}
//子树数量递增
tree.put(treeSub, count + 1);
return treeSub;
}
}
98. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
力扣第 98 题「 验证二叉搜索树」就是让你判断输入的 BST 是否合法。注意,这里是有坑的哦,按照 BST 左小右大的特性,每个节点想要判断自己是否是合法的
BST 节点,要做的事不就是比较自己和左右孩子吗?感觉应该这样写代码:
boolean isValidBST(TreeNode root) {
if (root == null) return true;
// root 的左边应该更小
if (root.left != null && root.left.val >= root.val)
return false;
// root 的右边应该更大
if (root.right != null && root.right.val <= root.val)
return false;
return isValidBST(root.left)
&& isValidBST(root.right);
}
但是这个算法出现了错误,BST 的每个节点应该要小于右边子树的所有节点,下面这个二叉树显然不是 BST,因为节点 10 的右子树中有一个节点 6,但是我们的
算法会把它判定为合法 BST:

出现问题的原因在于,对于每一个节点 root,代码值检查了它的左右孩子节点是否符合左小右大的原则;
但是根据 BST 的定义,root 的整个左子树都要小于 root.val,整个右子树都要大于 root.val。
问题是,对于某一个节点 root,他只能管得了自己的左右子节点,怎么把 root 的约束传递给左右子树呢?请看正确的代码:
boolean isValidBST(TreeNode root) {
return isValidBST(root, null, null);
}
/* 限定以 root 为根的子树节点必须满足 max.val > root.val > min.val */
boolean isValidBST(TreeNode root, TreeNode min, TreeNode max) {
// base case
if (root == null) return true;
// 若 root.val 不符合 max 和 min 的限制,说明不是合法 BST
if (min != null && root.val <= min.val) return false;
if (max != null && root.val >= max.val) return false;
// 限定左子树的最大值是 root.val,右子树的最小值是 root.val
return isValidBST(root.left, min, root)
&& isValidBST(root.right, root, max);
}
我们通过使用辅助函数,增加函数参数列表,在参数中携带额外信息,将这种约束传递给子树的所有节点,这也是二叉树算法的一个小技巧吧。
class Solution {
public boolean isValidBST(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
long preVal = Long.MIN_VALUE;
TreeNode node = root;
while (node != null || !stack.isEmpty()) {
if (node != null) {
stack.push(node);
node = node.left;
} else {
node = stack.pop();
// 当前值与上一次遍历到的值比较
// 当前值不大于上一次的值,那么就不符合二叉搜索树的性质了。
if (node.val <= preVal) {
return false;
}
// 记录遍历到的值
preVal = node.val;
node = node.right;
}
}
return true;
}
}
// 递归写法
// 通过使用辅助函数,增加函数参数列表,在参数中携带额外信息,将这种约束传递给子树的所有节点,这也是二叉树算法的一个小技巧吧。
// 感觉是在前序遍历时,
class Solution {
boolean isValidBST(TreeNode root) {
return isValidBST(root, null, null);
}
/* 限定以 root 为根的子树节点必须满足 max.val > root.val > min.val */
boolean isValidBST(TreeNode root, TreeNode min, TreeNode max) {
// base case
if (root == null) {
return true;
}
// 若 root.val 不符合 max 和 min 的限制,说明不是合法 BST
if (min != null && root.val <= min.val) {
return false;
}
if (max != null && root.val >= max.val) {
return false;
}
// 限定左子树的最大值是 root.val,右子树的最小值是 root.val
return isValidBST(root.left, min, root) && isValidBST(root.right, root, max);
}
}
// 用中序遍历的递归方法记录
class Solution {
private long prev = Long.MIN_VALUE;
public boolean isValidBST(TreeNode root) {
if (root == null) {
return true;
}
if (!isValidBST(root.left)) {
return false;
}
if (root.val <= prev) { // 不满足二叉搜索树条件
return false;
}
prev = root.val;
return isValidBST(root.right);
}
}
700. 二叉搜索树中的搜索(遍历)
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
class Solution {
// 迭代,利用二叉搜索树特点,优化,可以不需要栈
public TreeNode searchBST(TreeNode root, int val) {
while (root != null)
if (val < root.val) {
root = root.left;
}
else if (val > root.val) {
root = root.right;
} else {
return root;
}
return root;
}
}
// 递归
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
if (root == null) {
return null;
}
if (root.val < val) {
return searchBST(root.right, val);
}
if (root.val > val) {
return searchBST(root.left, val);
}
return root;
}
}
701. 二叉搜索树中的插入操作(遍历)
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉
搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
// 当树为空时,插入新的节点。
if (root == null) {
return new TreeNode(val);
}
TreeNode newRoot = root;
TreeNode cur = root;
TreeNode pre = root;
while (cur != null) {
pre = cur;
if (cur.val > val) {
cur = cur.left;
} else {
cur = cur.right;
}
}
// 如果要前一个节点的值大于要插入的值,那么就将新节点插入在左边。
if (pre.val > val) {
pre.left = new TreeNode(val);
} else {
// 如果要前一个节点的值小于要插入的值,那么就将新节点插入在右边。
pre.right = new TreeNode(val);
}
return newRoot;
}
}
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
if (root == null) {
return new TreeNode(val);
}
if (root.val > val) {
root.left = insertIntoBST(root.left, val);
}
if (root.val < val) {
root.right = insertIntoBST(root.right, val);
}
return root;
}
}
450. 删除二叉搜索树中的节点⭐⭐⭐
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根
节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
这个问题稍微复杂,跟插入操作类似,先「找」再「改」,先把框架写出来再说:
TreeNode deleteNode(TreeNode root, int key) {
if (root.val == key) {
// 找到啦,进行删除
} else if (root.val > key) {
// 去左子树找
root.left = deleteNode(root.left, key);
} else if (root.val < key) {
// 去右子树找
root.right = deleteNode(root.right, key);
}
return root;
}
找到目标节点了,比方说是节点 A,如何删除这个节点,这是难点。因为删除节点的同时不能破坏 BST 的性质。有三种情况,用图片来说明。
情况 1:A 恰好是末端节点,两个子节点都为空,那么它可以当场去世了。
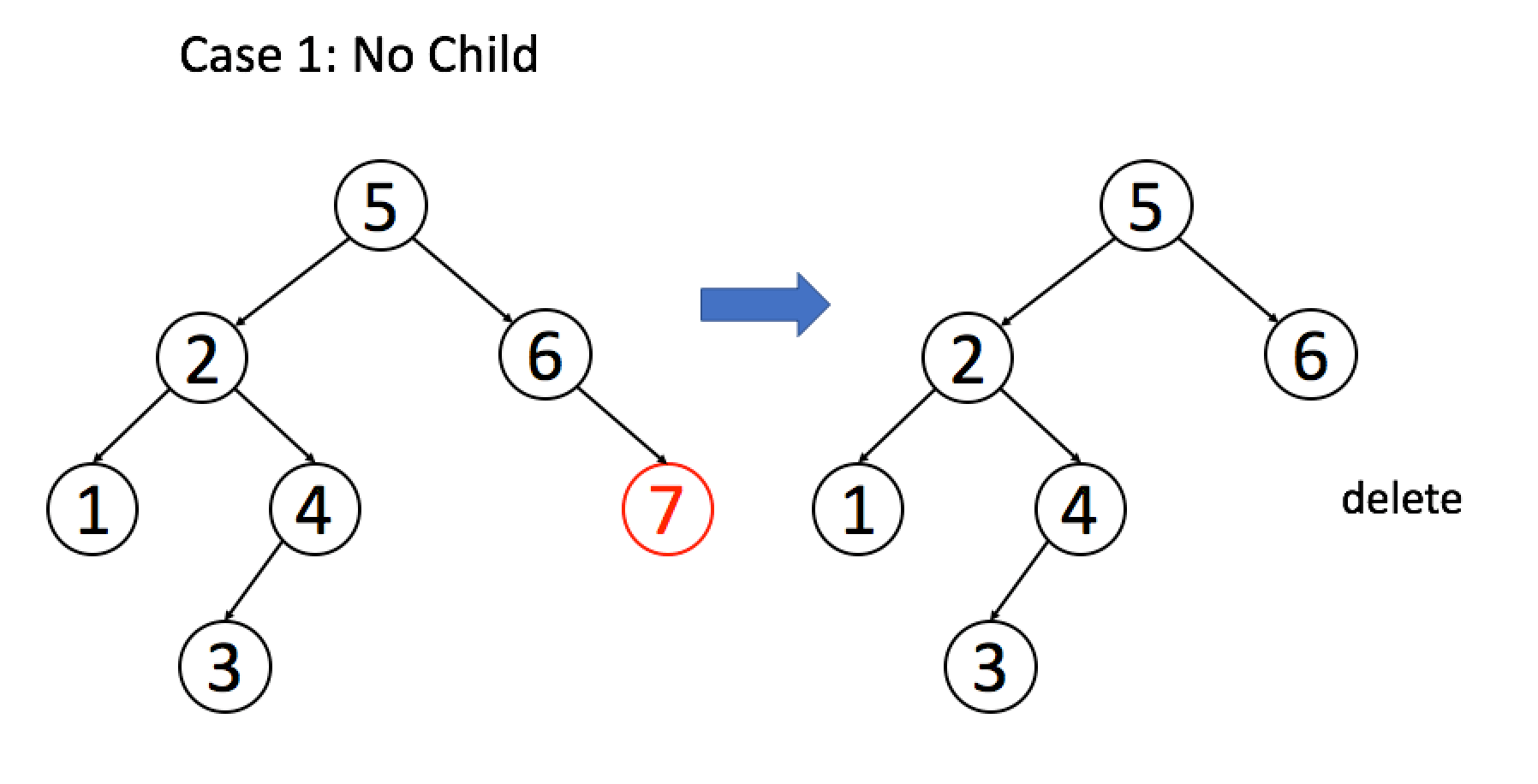
if (root.left == null && root.right == null)
return null;
情况 2:A 只有一个非空子节点,那么它要让这个孩子接替自己的位置。
// 排除了情况 1 之后
if (root.left == null) return root.right;
if (root.right == null) return root.left;
情况 3:A 有两个子节点,麻烦了,为了不破坏 BST 的性质,A 必须找到左子树中最大的那个节点,或者右子树中最小的那个节点来接替自己。我们以第二种方
式讲解。
if (root.left != null && root.right != null) {
// 找到右子树的最小节点
TreeNode minNode = getMin(root.right);
// 把 root 改成 minNode
root.val = minNode.val;
// 转而去删除 minNode
root.right = deleteNode(root.right, minNode.val);
}
三种情况分析完毕,填入框架,简化一下代码:
TreeNode deleteNode(TreeNode root, int key) {
if (root == null) return null;
if (root.val == key) {
// 这两个 if 把情况 1 和 2 都正确处理了
if (root.left == null) return root.right;
if (root.right == null) return root.left;
// 处理情况 3
// 获得右子树最小的节点
TreeNode minNode = getMin(root.right);
// 删除右子树最小的节点
root.right = deleteNode(root.right, minNode.val);
// 用右子树最小的节点替换 root 节点
minNode.left = root.left;
minNode.right = root.right;
root = minNode;
} else if (root.val > key) {
root.left = deleteNode(root.left, key);
} else if (root.val < key) {
root.right = deleteNode(root.right, key);
}
return root;
}
TreeNode getMin(TreeNode node) {
// BST 最左边的就是最小的
while (node.left != null) node = node.left;
return node;
}
这样,删除操作就完成了。注意一下,上述代码在处理情况 3 时通过一系列略微复杂的链表操作交换 root 和 minNode 两个节点:
// 处理情况 3
// 获得右子树最小的节点
TreeNode minNode = getMin(root.right);
// 删除右子树最小的节点
root.right = deleteNode(root.right, minNode.val);
// 用右子树最小的节点替换 root 节点
minNode.left = root.left;
minNode.right = root.right;
root = minNode;
有的读者可能会疑惑,替换 root 节点为什么这么麻烦,直接改 val 字段不就行了?看起来还更简洁易懂:
// 处理情况 3
// 获得右子树最小的节点
TreeNode minNode = getMin(root.right);
// 删除右子树最小的节点
root.right = deleteNode(root.right, minNode.val);
// 用右子树最小的节点替换 root 节点
root.val = minNode.val;
仅对于这道算法题来说是可以的,但这样操作并不完美,我们一般不会通过修改节点内部的值来交换节点。因为在实际应用中,BST 节点内部的数据域是用户自定义的,可以非常复杂,而 BST 作为数据结构(一个工具人),其操作应该和内部存储的数据域解耦,所以我们更倾向于使用指针操作来交换节点,根本没必要关心内部数据。
最后总结一下吧,通过这篇文章,我们总结出了如下几个技巧:
1、如果当前节点会对下面的子节点有整体影响,可以通过辅助函数增长参数列表,借助参数传递信息。
2、在二叉树递归框架之上,扩展出一套 BST 代码框架:
void BST(TreeNode root, int target) {
if (root.val == target)
// 找到目标,做点什么
if (root.val < target)
BST(root.right, target);
if (root.val > target)
BST(root.left, target);
}
3、根据代码框架掌握了 BST 的增删查改操作。
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null) {
return null;
}
if (root.val == key) {
// 左右子树都为空,叶子节点直接删除。
if (root.left == null && root.right == null) {
return null;
}
// 左子树为空,右子树接替被删除节点的位置。
if (root.left == null) {
return root.right;
}
// 右子树为空,左子树接替被删除节点的位置。
if (root.right == null) {
return root.left;
}
// 左右子树都不为空。
// 找到删除节点右子树上最小的节点
TreeNode minNode = getMinNode(root.right);
// 删除右子树最小的节点
root.right = deleteNode(root.right, minNode.val);
minNode.left = root.left;
minNode.right = root.right;
// 因为要向上返回处理之后的节点root
root = minNode;
} else if (root.val > key) { // 递归到左子树上删除
root.left = deleteNode(root.left, key);
} else if (root.val < key) { // 递归到右子树上删除
root.right = deleteNode(root.right, key);
}
return root;
}
private TreeNode getMinNode(TreeNode root) {
while (root.left != null) {
root = root.left;
}
return root;
}
}
863. 二叉树中所有距离为 K 的结点(BFS)⭐⭐⭐
给定一个二叉树(具有根结点 root), 一个目标结点 target ,和一个整数值 k 。
返回到目标结点 target 距离为 k 的所有结点的值的列表。 答案可以以 任何顺序 返回。
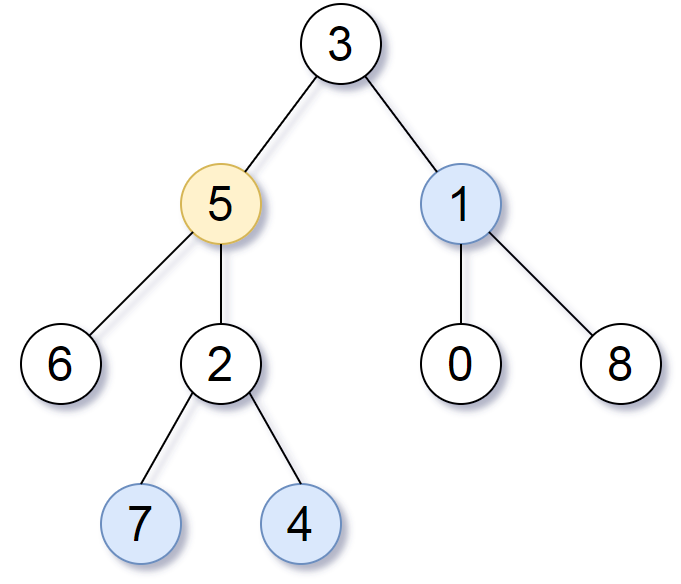
class Solution {
// 记录父节点:node.val -> parentNode
// 题目说了树中所有节点值都是唯一的,所以可以用 node.val 代表 TreeNode
HashMap<Integer, TreeNode> parent = new HashMap<>();
public List<Integer> distanceK(TreeNode root, TreeNode target, int k) {
// 遍历所有节点,记录每个节点的父节点
traverse(root, null);
// 开始从 target 节点施放 BFS 算法,找到距离为 k 的节点
Queue<TreeNode> queue = new LinkedList<>();
HashSet<Integer> visited = new HashSet<>();
queue.offer(target);
visited.add(target.val);
// 记录离 target 的距离
int distance = 0;
List<Integer> res = new LinkedList<>();
while (!queue.isEmpty()) {
int sz = queue.size();
for (int i = 0; i < sz; i++) {
TreeNode cur = queue.poll();
if (distance == k) {
// 找到距离起点 target 距离为 k 的节点
res.add(cur.val);
}
// 向父节点、左右子节点扩散
TreeNode parentNode = parent.get(cur.val);
if (parentNode != null && !visited.contains(parentNode.val)) {
visited.add(parentNode.val);
queue.offer(parentNode);
}
if (cur.left != null && !visited.contains(cur.left.val)) {
visited.add(cur.left.val);
queue.offer(cur.left);
}
if (cur.right != null && !visited.contains(cur.right.val)) {
visited.add(cur.right.val);
queue.offer(cur.right);
}
}
// 向外扩展一圈
distance++;
}
return res;
}
private void traverse(TreeNode root, TreeNode parentNode) {
if (root == null) {
return;
}
parent.put(root.val, parentNode);
// 二叉树递归框架
traverse(root.left, root);
traverse(root.right, root);
}
}
剑指 Offer 33. 二叉搜索树的后序遍历序列
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
解题思路:
我们反向遍历数组,
class Solution {
public boolean verifyPostorder(int[] postorder) {
// 单调栈使用,单调递增的单调栈
Deque<Integer> stack = new LinkedList<>();
int pervElem = Integer.MAX_VALUE;
// 逆向遍历,就是左右翻转的先序遍历
// 先序遍历是中左右
// 后序遍历是左右中
// 反转后序遍历是中右左
for (int i = postorder.length - 1; i >= 0; i--) {
// 左子树元素必须要小于递增栈被peek访问的元素,否则就不是二叉搜索树。
if (postorder[i] > pervElem) {
return false;
}
while (!stack.isEmpty() && postorder[i] < stack.peek()) {
// 数组元素小于单调栈的元素了,表示往左子树走了,记录下上个根节点
// 找到这个左子树对应的根节点,之前右子树全部弹出,不再记录,因为不可能再往根节点的右子树走了
pervElem = stack.pop();
}
// 这个新元素入栈
stack.push(postorder[i]);
}
return true;
}
}
字典树相关
前缀树」又叫「字典树」或「单词查找树」,总之它们是一个意思!
「前缀树」的应用场景:给定一个字符串集合构建一棵前缀树,然后给一个字符串,判断前缀树中是否存在该字符串或者该字符串的前缀。
一般而言,字符串的集合都是仅由小写字母构成,所以本文章都是基于该情况展开分析!
字符串集合:[them, zip, team, the, app, that]。这个样例的前缀树长什么样呢?
由于都是小写字母,所以对于每个节点,均有 26 个孩子节点,上图中没有画出来,省略了而已...,但是要记住:每个节点均有 26 个孩子节点
还有一个点要明确:节点仅仅表示从根节点到本节点的路径构成的字符串是否有效而已。
对于上图中橙色的节点,均为有效节点,即:从根节点到橙色节点的路径构成的字符串均在集合中
如果现在要找前缀 te 是否存在,分两步:
首先看看表示 te 字符串的路径是否存在,这个例子是存在的
其次看看该路径的终点处的节点是否有效,很遗憾,此处为白色,无效
所以前缀 te 不存在!!
现在看看如何表示这棵「前缀树」,即数据结构该如何定义。其实就是一棵多叉树,有 26 个孩子节点的多叉树而已!!
现在来思考节点的值又该如何表示呢?
在上面的例子中,节点仅仅表示路径构成的字符串是否有效而已,所以节点可以用 boolean 类型来表示。
还有一类情况就是每个字符串都有一个权值,所以节点的值可以用一个数值来表示
// 前缀树的数据结构
class TrieNode {
boolean val;
TrieNode[] children = new TrieNode[26];
}
// 前缀树的根节点
private TrieNode root = new TrieNode();
根据上面的分析,其实「前缀树」常用操作就三种
- 根据所给字符串集合构建前缀树;
- 判断前缀树中是否存在目标字符串;
- 在前缀树中找出目标字符串的最短前缀。
构建前缀树
// 往前缀树中插入一个新的字符串
public void insert(String word) {
TrieNode p = root;
for (char c : word.toCharArray()) {
// char -> int
int i = c - 'a';
// 初始化孩子节点
if (p.children[i] == null) {
p.children[i] = new TrieNode();
}
// 节点下移
p = p.children[i];
}
// 此时 p 指向目标字符串的终点
p.val = true;
}
寻找目标字符串
当「前缀树」构建好了后,寻找目标字符串也就大同小异了
复习一下寻找的两个步骤:
- 首先看看表示字符串的路径是否存在;
- 其次看看该路径的终点处的节点是否有效。
public boolean query(String word) {
TrieNode p = root;
for (char c : word.toCharArray()) {
int i = c - 'a';
// 路径不存在的情况,直接返回 false
if (p.children[i] == null) {
return false;
}
p = p.children[i];
}
// 路径存在,直接返回该路径的终点处的节点的有效性
return p.val;
}
寻找最短前缀
和「寻找目标字符串」差不多,但又有些许不同。
「寻找目标字符串」必须遍历到目标字符串的末尾,然后再判断路径是否有效。
「寻找最短前缀」只要在遍历的过程有中,首次出现了有效路径,即为找到!!
public String shortestPrefixOf(String word) {
TrieNode p = root;
StringBuffer sb = new StringBuffer();
for (char c : word.toCharArray()) {
int i = c - 'a';
// 首次遇到有效路径,直接返回
if (p.val) {
return sb.toString();
}
ans.append(c);
// 路径不存在的情况,直接返回 ""
if (p.children[i] == null) {
return "";
}
p = p.children[i];
}
// 没找到
return "";
}
含有通配符的寻找
public String keysWithPattern(TrieNode node, String pattern, int index) {
int i = pattern.charAt(index) - 'a';
if (pattern.charAt(index) == '.') {
for (int j = 0; j < 26; j++) {
if (keysWithPattern(node.children[j], pattern, index + 1)) {
return true;
}
}
return false;
} else {
return keysWithPattern(node.children[i], pattern, index + 1);
}
}
208. 实现 Trie (前缀树)
class Trie {
class TireNode {
boolean val;
TireNode[] children = new TireNode[26];
}
TireNode root;
public Trie() {
root = new TireNode();
}
public void insert(String word) {
TireNode p = root;
for (char c : word.toCharArray()) {
int i = c - 'a';
if (p.children[i] == null) {
p.children[i] = new TireNode();
}
p = p.children[i];
}
p.val = true;
}
public boolean search(String word) {
TireNode p = root;
for (char c : word.toCharArray()) {
int i = c - 'a';
if (p.children[i] == null) {
return false;
}
p = p.children[i];
}
return p.val;
}
public boolean startsWith(String prefix) {
TireNode p = root;
for (char c : prefix.toCharArray()) {
int i = c - 'a';
if (p.children[i] == null) {
return false;
}
p = p.children[i];
}
return true;
}
}
648. 单词替换
在英语中,我们有一个叫做 词根(root) 的概念,可以词根后面添加其他一些词组成另一个较长的单词——我们称这个词为 继承词(successor)。
例如,词根an,跟随着单词 other(其他),可以形成新的单词 another(另一个)。
现在,给定一个由许多词根组成的词典 dictionary 和一个用空格分隔单词形成的句子 sentence。你需要将句子中的所有继承词用词根替换掉。
如果继承词有许多可以形成它的词根,则用最短的词根替换它。你需要输出替换之后的句子。
输入:dictionary = ["cat","bat","rat"], sentence = "the cattle was rattled by the battery"
输出:"the cat was rat by the bat"
class Solution {
public String replaceWords(List<String> dictionary, String sentence) {
// 将dictionary中的单词插入前缀树中
for (String str : dictionary) {
insert(str);
}
StringBuilder sb = new StringBuilder();
// 将句子中的单词分割出来
String[] strings = sentence.split(" ");
for (int i = 0; i < strings.length; i++) {
String res = shortestPrefixOf(strings[i]);
if (res == "") {
sb.append(strings[i]).append(" ");
} else {
sb.append(res).append(" ");
}
}
// 删除最后的空格转为字符串返回
return sb.deleteCharAt(sb.length() - 1).toString();
}
class TrieNode {
boolean val;
TrieNode[] children = new TrieNode[26];
}
TrieNode root = new TrieNode();
public void insert(String word) {
TrieNode p = root;
for (char c : word.toCharArray()) {
int i = c - 'a';
if (p.children[i] == null) {
p.children[i] = new TrieNode();
}
p = p.children[i];
}
p.val = true;
}
// 寻找word在字典树中的最短前缀。
public String shortestPrefixOf(String word) {
TrieNode p = root;
StringBuilder sb = new StringBuilder();
for (char ch : word.toCharArray()) {
int i = ch - 'a';
if (p.val) {
return sb.toString();
}
sb.append(ch);
if (p.children[i] == null) {
return "";
}
p = p.children[i];
}
return "";
}
}
211. 添加与搜索单词 - 数据结构设计
请你设计一个数据结构,支持 添加新单词 和 查找字符串是否与任何先前添加的字符串匹配 。
实现词典类 WordDictionary :
- WordDictionary() 初始化词典对象
- void addWord(word) 将 word 添加到数据结构中,之后可以对它进行匹配
- bool search(word) 如果数据结构中存在字符串与 word 匹配,则返回 true ;否则,返回 false 。word 中可能包含一些 '.' ,每个 . 都可以表示任何一个字母。
class WordDictionary {
class TrieNode {
boolean val;
TrieNode[] children = new TrieNode[26];
}
TrieNode root;
public WordDictionary() {
root = new TrieNode();
}
public void addWord(String word) {
TrieNode p = root;
for (char ch : word.toCharArray()) {
int i = ch - 'a';
if (p.children[i] == null) {
p.children[i] = new TrieNode();
}
p = p.children[i];
}
p.val = true;
}
public boolean search(String word) {
return keysWithPattern(root, word, 0);
}
public boolean keysWithPattern(TrieNode node, String pattern, int index) {
if (node == null) {
return false;
}
// 当index == pattern.length()并不一定是找到了某个单词
// 也许是某个单词的一部分,所以还得查看在这个位置是否被标记为单词的结束即node.val是否为true。
if (index == pattern.length()) {
return node.val;
}
int i = pattern.charAt(index) - 'a';
if (pattern.charAt(index) == '.') {
// 若是遇到字符'.'那么26个字母都可以匹配
for (int j = 0; j < 26; j++) {
if (keysWithPattern(node.children[j], pattern, index + 1)) {
return true;
}
}
return false;
} else {
return keysWithPattern(node.children[i], pattern, index + 1);
}
}
}
677. 键值映射
设计一个 map ,满足以下几点:
- 字符串表示键,整数表示值;
- 返回具有前缀等于给定字符串的键的值的总和。
实现一个 MapSum 类:
-
MapSum() 初始化 MapSum 对象;
-
void insert(String key, int val) 插入 key-val 键值对,字符串表示键 key ,整数表示值 val 。
如果键 key 已经存在,那么原来的键值对 key-value 将被替代成新的键值对;
-
int sum(string prefix) 返回所有以该前缀 prefix 开头的键 key 的值的总和。
class MapSum {
class TrieNode {
int val;
TrieNode[] children = new TrieNode[26];
}
TrieNode root;
public MapSum() {
root = new TrieNode();
}
public void insert(String key, int val) {
TrieNode p = root;
for (char c : key.toCharArray()) {
int i = c - 'a';
if (p.children[i] == null) {
p.children[i] = new TrieNode();
}
p = p.children[i];
}
p.val = val;
}
public int sum(String prefix) {
TrieNode p = root;
// 找到前缀 prefix 的最后一个节点
for (char c : prefix.toCharArray()) {
int i = c - 'a';
if (p.children[i] == null) {
return 0;
}
p = p.children[i];
}
//
return getAllSum(p);
}
// 辅助函数,求以 node 为根节点的子树的节点和
private int getAllSum(TrieNode node) {
if (node == null) {
return 0;
}
int sum = 0;
// DFS
for (int i = 0; i < 26; i++) {
sum += getAllSum(node.children[i]);
}
return sum + node.val;
}
}
676. 实现一个魔法字典
设计一个使用单词列表进行初始化的数据结构,单词列表中的单词 互不相同 。
如果给出一个单词,请判定能否只将这个单词中一个字母换成另一个字母,使得所形成的新单词存在于你构建的字典中。
实现 MagicDictionary 类:
- MagicDictionary() 初始化对象;
- void buildDict(String[] dictionary) 使用字符串数组 dictionary 设定该数据结构,dictionary 中的字符串互不相同;
- bool search(String searchWord) 给定一个字符串 searchWord ,判定能否只将字符串中 一个 字母换成另一个字母,使得所形成的新字符串能够与字典中的任一字符串匹配。如果可以,返回 true ;否则,返回 false 。
class MagicDictionary {
class TrieNode {
boolean val;
TrieNode[] children = new TrieNode[26];
}
TrieNode root;
public MagicDictionary() {
root = new TrieNode();
}
public void buildDict(String[] dictionary) {
for (String str : dictionary) {
TrieNode p = root;
for (char c : str.toCharArray()) {
int i = c - 'a';
if (p.children[i] == null) {
p.children[i] = new TrieNode();
}
p = p.children[i];
}
p.val = true;
}
}
public boolean search(String searchWord) {
// 遍历每一种替换的情况
for (int i = 0; i < searchWord.length(); i++) {
if (search(root, searchWord, 0, i)) {
return true;
}
}
return false;
}
private boolean search(TrieNode node, String searchWord, int index, int start) {
if (node == null) {
return false;
}
if (index == searchWord.length()) {
return node.val;
}
int i = searchWord.charAt(index) - 'a';
// 匹配到我们打算要替换的那个字符的索引位置
// 在这个字符所在字典树对应的children数组里除了i位置不继续往下搜索之外,其余位置都要尝试搜索。
// 为什么不继续搜索i这个位置,因为如果i这个位置对应的字符正好被字典树中的某一个字符串包含。
// 最终能够搜索到这一个完整的字符串,可是这样不符合search函数的语义,这个函数返回是否能够改变
// searchWord中的一个字符与字典中的字符匹配。如果searchWord和字典中的一个字符串一样。
// search函数应该返回false才对。
if (index == start) {
for (int j = 0; j < 26; j++) {
if (i == j) {
continue;
}
if (search(node.children[j], searchWord, index + 1, start)) {
return true;
}
}
return false;
} else {
return search(node.children[i], searchWord, index + 1, start);
}
}
}
DFS
200. 岛屿数量
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
class Solution {
public int numIslands(char[][] grid) {
int count = 0;
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == '1') {
dfs(grid, i, j);
count++;
}
}
}
return count;
}
private void dfs(char[][] grid, int i, int j) {
if (!inArea(grid, i, j)) {
return;
}
if (grid[i][j] != '1') {
return;
}
grid[i][j] = '2';
// 往四个方向dfs把属于这个岛屿的陆地格子都标记为访问过的
dfs(grid, i + 1, j);
dfs(grid, i, j + 1);
dfs(grid, i - 1, j);
dfs(grid, i, j - 1);
}
private boolean inArea(char[][] grid, int i, int j) {
return i >= 0 && i < grid.length && j >= 0 && j < grid[0].length;
}
}
1254. 统计封闭岛屿的数目
二维矩阵 grid 由 0 (土地)和 1 (水)组成。岛是由最大的4个方向连通的 0 组成的群,封闭岛是一个 完全 由1包围(左、上、右、下)的岛。
请返回封闭岛屿的数目。
那么如何判断「封闭岛屿」呢?其实很简单,把上一题中那些靠边的岛屿排除掉,剩下的不就是「封闭岛屿」了吗?
有了这个思路,就可以直接看代码了,注意这题规定 0 表示陆地,用 1 表示海水:
class Solution {
public int closedIsland(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
for (int j = 0; j < n; j++) {
dfs(grid, 0, j);
dfs(grid, m - 1, j);
}
for (int i = 0; i < m; i++) {
dfs(grid, i, 0);
dfs(grid, i, n - 1);
}
int count = 0;
for (int i = 1; i < m - 1; i++) {
for (int j = 1; j < n - 1; j++) {
if (grid[i][j] == 0) {
dfs(grid, i, j);
count++;
}
}
}
return count;
}
private void dfs(int[][] grid, int i, int j) {
if (!inArea(grid, i, j)) {
return;
}
if (grid[i][j] != 0) {
return;
}
grid[i][j] = 2;
dfs(grid, i - 1, j);
dfs(grid, i + 1, j);
dfs(grid, i, j - 1);
dfs(grid, i, j + 1);
}
private boolean inArea(int[][] grid, int i, int j) {
return i >= 0 && i < grid.length && j >= 0 && j < grid[0].length;
}
}
1020. 飞地的数量
// 就是求封闭岛屿的陆地总数
class Solution {
public int numEnclaves(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
for (int j = 0; j < n; j++) {
dfs(grid, 0, j);
dfs(grid, m - 1, j);
}
for (int i = 0; i < m; i++) {
dfs(grid, i, 0);
dfs(grid, i, n - 1);
}
int res = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
res++;
}
}
}
return res;
}
private void dfs(int[][] grid, int i, int j) {
if (!inArea(grid, i, j)) {
return;
}
if (grid[i][j] != 1) {
return;
}
grid[i][j] = 2;
dfs(grid, i - 1, j);
dfs(grid, i + 1, j);
dfs(grid, i, j - 1);
dfs(grid, i, j + 1);
}
private boolean inArea(int[][] grid, int i, int j) {
return i >= 0 && i < grid.length && j >= 0 && j < grid[0].length;
}
}
130. 被围绕的区域
给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' ,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
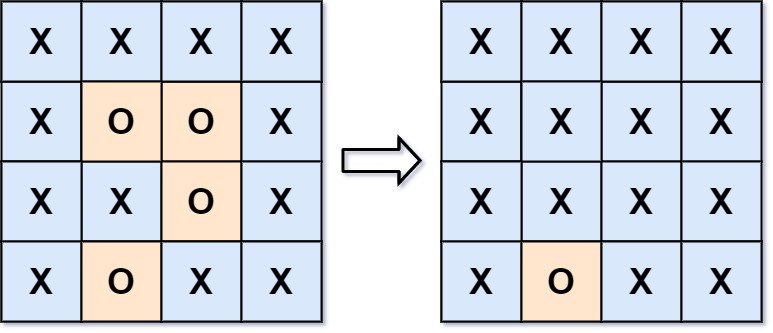
class Solution {
public void solve(char[][] board) {
int m = board.length;
int n = board[0].length;
for (int j = 0; j < n; j++) {
dfs1(board, 0, j);
dfs1(board, m - 1, j);
}
for (int i = 0; i < m; i++) {
dfs1(board, i, 0);
dfs1(board, i, n - 1);
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (board[i][j] == 'O') {
dfs2(board, i, j);
}
}
}
for (int j = 0; j < n; j++) {
dfs3(board, 0, j);
dfs3(board, m - 1, j);
}
for (int i = 0; i < m; i++) {
dfs3(board, i, 0);
dfs3(board, i, n - 1);
}
}
private void dfs1(char[][] board, int i, int j) {
if (!inArea(board, i, j)) {
return;
}
if (board[i][j] != 'O') {
return;
}
board[i][j] = 'P';
dfs1(board, i - 1, j);
dfs1(board, i + 1, j);
dfs1(board, i, j - 1);
dfs1(board, i, j + 1);
}
private void dfs2(char[][] board, int i, int j) {
if (!inArea(board, i, j)) {
return;
}
if (board[i][j] != 'O') {
return;
}
board[i][j] = 'X';
dfs2(board, i + 1, j);
dfs2(board, i - 1, j);
dfs2(board, i, j - 1);
dfs2(board, i, j + 1);
}
private void dfs3(char[][] board, int i, int j) {
if (!inArea(board, i, j)) {
return;
}
if (board[i][j] != 'P') {
return;
}
board[i][j] = 'O';
dfs3(board, i + 1, j);
dfs3(board, i - 1, j);
dfs3(board, i, j + 1);
dfs3(board, i, j - 1);
}
private boolean inArea(char[][] board, int i, int j) {
return i >= 0 && i < board.length && j >= 0 && j < board[0].length;
}
}
695. 岛屿的最大面积
给你一个大小为 m x n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。
你可以假设 grid 的四个边缘都被 0(代表水)包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
这题的大体思路和之前完全一样,只不过 dfs 函数淹没岛屿的同时,还应该想办法记录这个岛屿的面积。
我们可以给 dfs 函数设置返回值,记录每次淹没的陆地的个数,直接看解法吧:
class Solution {
public int maxAreaOfIsland(int[][] grid) {
int res = 0;
for (int row = 0; row < grid.length; row++) {
for (int column = 0; column < grid[0].length; column++) {
if (grid[row][column] == 1) {
int a = dfs(grid, row, column);
res = Math.max(res, a);
}
}
}
return res;
}
int dfs(int[][] grid, int i, int j) {
if (!inArea(grid, i, j)) {
return 0;
}
// 如果遍历到的不是陆地格子,而是海洋或者已经遍历过的陆地格子,直接返回。
if (grid[i][j] != 1) {
return 0;
}
// 遍历过的格子标记为2,就不会重复遍历
grid[i][j] = 2;
return 1 + dfs(grid, i - 1, j) + dfs(grid, i + 1, j) + dfs(grid, i, j - 1) + dfs(grid, i, j + 1);
}
// 是否在网格范围内
boolean inArea(int[][] grid, int i, int j) {
return i >= 0 && i < grid.length && j >= 0 && j < grid[0].length;
}
}
463. 岛屿的周长⭐⭐⭐
给定一个 row x col 的二维网格地图 grid ,其中:grid[i][j] = 1 表示陆地, grid[i][j] = 0 表示水域。
网格中的格子 水平和垂直 方向相连(对角线方向不相连)。
整个网格被水完全包围,但其中恰好有一个岛屿(或者说,一个或多个表示陆地的格子相连组成的岛屿)。
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。
网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
实话说,这道题用 DFS 来解并不是最优的方法。对于岛屿,直接用数学的方法求周长会更容易。
不过这道题是一个很好的理解 DFS 遍历过程的例题,不信你跟着我往下看。
我们再回顾一下 网格 DFS 遍历的基本框架:
void dfs(int[][] grid, int r, int c) {
// 判断 base case
if (!inArea(grid, r, c)) {
return;
}
// 如果这个格子不是岛屿,直接返回
if (grid[r][c] != 1) {
return;
}
grid[r][c] = 2; // 将格子标记为「已遍历过」
// 访问上、下、左、右四个相邻结点
dfs(grid, r - 1, c);
dfs(grid, r + 1, c);
dfs(grid, r, c - 1);
dfs(grid, r, c + 1);
}
// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {
return 0 <= r && r < grid.length
&& 0 <= c && c < grid[0].length;
}
可以看到,dfs 函数直接返回有这几种情况:
- !inArea(grid, r, c),即坐标 (r, c) 超出了网格的范围,也就是我所说的「先污染后治理」的情况;
- grid[r] [c] != 1,即当前格子不是岛屿格子,这又分为两种情况:
- grid[r] [c] == 0,当前格子是海洋格子;
- grid[r] [c] == 2,当前格子是已遍历的陆地格子。
那么这些和我们岛屿的周长有什么关系呢?实际上,岛屿的周长是计算岛屿全部的「边缘」,而这些边缘就是我们在 DFS 遍历中,dfs 函数返回的位置。观察题目
示例,我们可以将岛屿的周长中的边分为两类,如下图所示。黄色的边是与网格边界相邻的周长,而蓝色的边是与海洋格子相邻的周长。
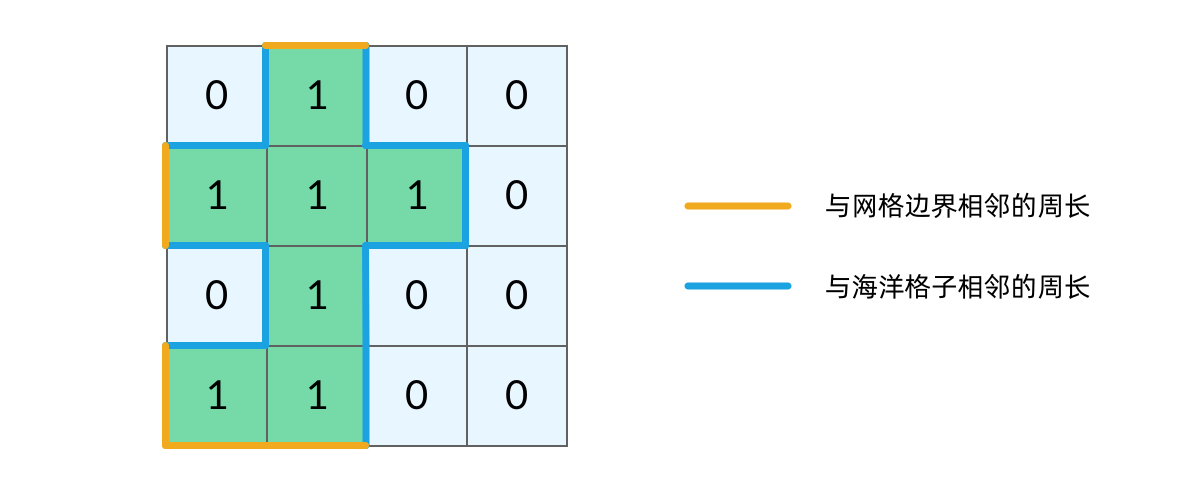
当我们的 dfs 函数因为「坐标 (r, c) 超出网格范围」返回的时候,实际上就经过了一条黄色的边;而当函数因为「当前格子是海洋格子」返回的时候,实际上就经
过了一条蓝色的边。这样,我们就把岛屿的周长跟 DFS 遍历联系起来了,我们的题解代码也呼之欲出:
class Solution {
public int islandPerimeter(int[][] grid) {
for (int r = 0; r < grid.length; r++) {
for (int c = 0; c < grid[0].length; c++) {
if (grid[r][c] == 1) {
// 题目限制只有一个岛屿,计算一个即可。
return dfs(grid, r, c);
}
}
}
return 0;
}
int dfs(int[][] grid, int r, int c) {
// 函数因为「坐标 (r, c) 超出网格范围」返回,对应一条黄色的边。
if (!inArea(grid, r, c)) {
return 1;
}
// 函数因为「当前格子是海洋格子」返回,对应一条蓝色的边。
if (grid[r][c] == 0) {
return 1;
}
// 函数因为「当前格子是已遍历的陆地格子」返回,和周长没关系。
if (grid[r][c] == 2) {
return 0;
}
grid[r][c] = 2;
return dfs(grid, r - 1, c) + dfs(grid, r + 1, c) + dfs(grid, r, c - 1) + dfs(grid, r, c + 1);
}
// 判断坐标 (r, c) 是否在网格中。
boolean inArea(int[][] grid, int r, int c) {
return 0 <= r && r < grid.length && 0 <= c && c < grid[0].length;
}
}
827. 最大人工岛⭐⭐⭐
给你一个大小为 n x n 二进制矩阵 grid 。最多 只能将一格 0 变成 1 。
返回执行此操作后,grid 中最大的岛屿面积是多少?
岛屿 由一组上、下、左、右四个方向相连的 1 形成。
输入: grid = [[1, 0], [0, 1]]
输出: 3
解释: 将一格0变成1,最终连通两个小岛得到面积为 3 的岛屿。
这道题是岛屿最大面积问题的升级版。现在我们有填海造陆的能力,可以把一个海洋格子变成陆地格子,进而让两块岛屿连成一块。
那么填海造陆之后,最大可能构造出多大的岛屿呢?
大致的思路我们不难想到,我们先计算出所有岛屿的面积,在所有的格子上标记出岛屿的面积。然后搜索哪个海洋格子相邻的两个岛屿面积最大。
例如下图中红色方框内的海洋格子,上边、左边都与岛屿相邻,我们可以计算出它变成陆地之后可以连接成的岛屿面积为 7+1+2=10。
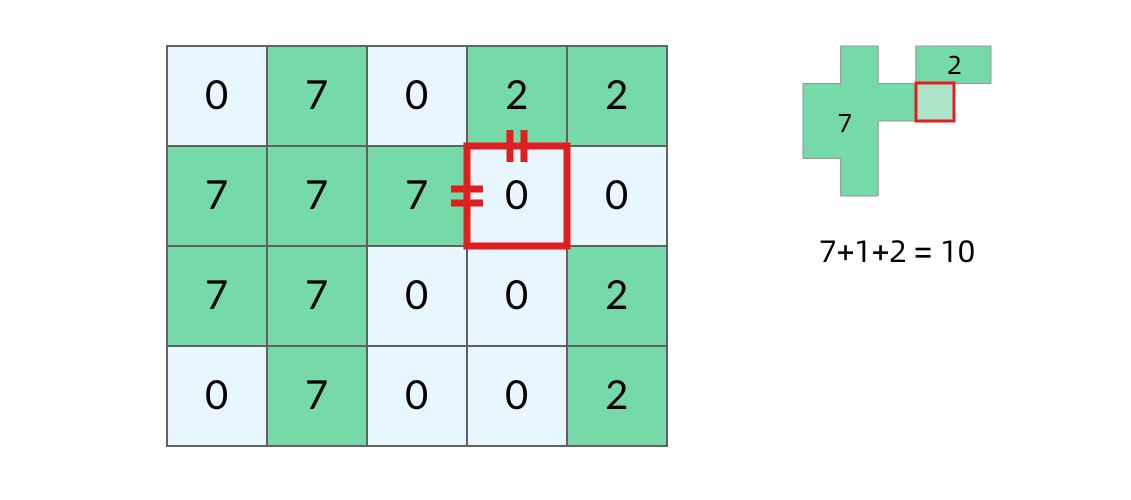
然而,这种做法可能遇到一个问题。如下图中红色方框内的海洋格子,它的上边、左边都与岛屿相邻,这时候连接成的岛屿面积难道是 7+1+7 ?显然不是。这两
个 7 来自同一个岛屿,所以填海造陆之后得到的岛屿面积应该只有 7+1 = 8。
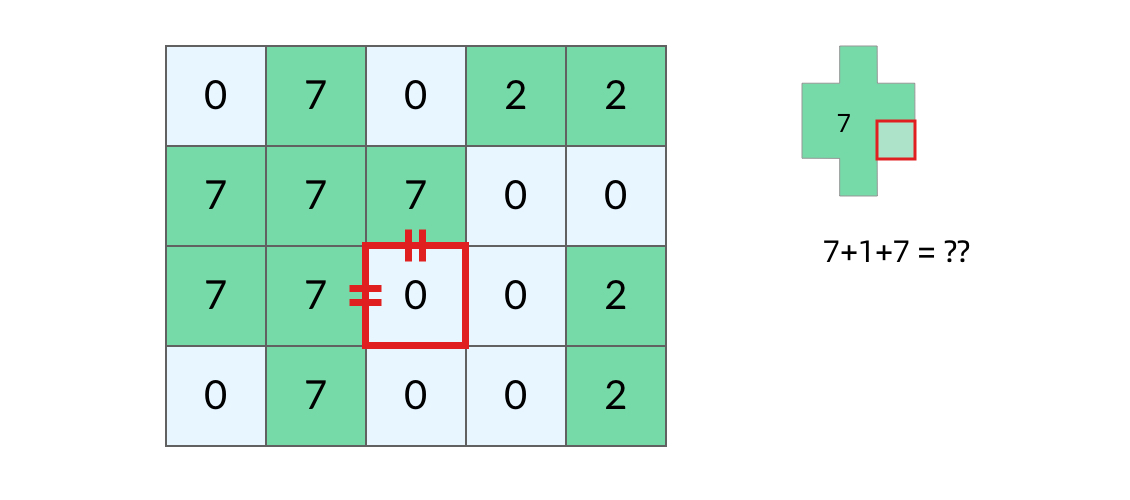
可以看到,要让算法正确,我们得能区分一个海洋格子相邻的两个 7 是不是来自同一个岛屿。
那么,我们不能在方格中标记岛屿的面积,而应该标记岛屿的索引(下标),另外用一个数组记录每个岛屿的面积,如下图所示。
这样我们就可以发现红色方框内的海洋格子,它的「两个」相邻的岛屿实际上是同一个。
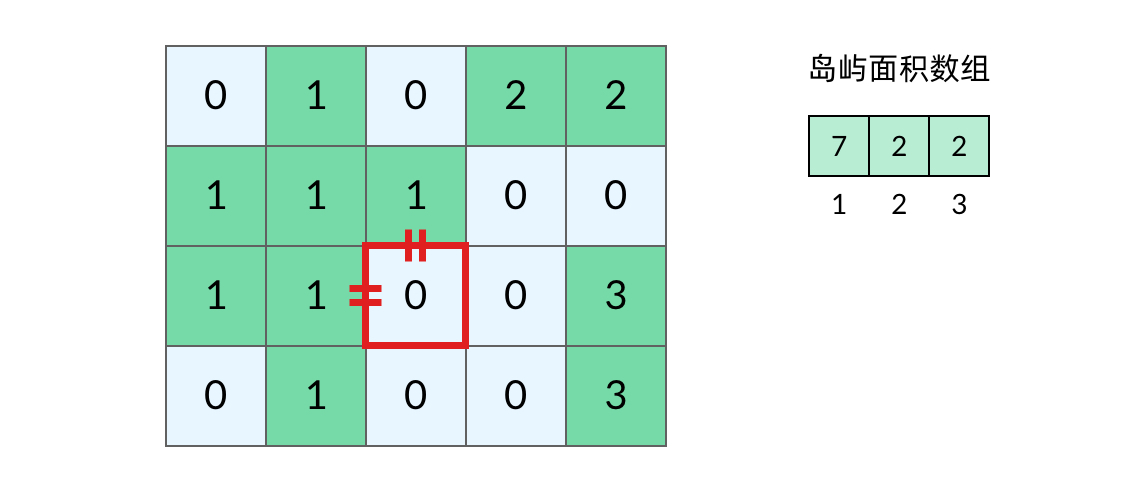
可以看到,这道题实际上是对网格做了两遍 DFS:
第一遍 DFS 遍历陆地格子,计算每个岛屿的面积并标记岛屿;
第二遍 DFS 遍历海洋格子,观察每个海洋格子相邻的陆地格子。
class Solution {
HashMap<Integer, Integer> indexAreaMap = new HashMap<>();
public int largestIsland(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int res = 0;
int index = 2;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
int area = dfs(grid, index, i, j);
indexAreaMap.put(index, area);
index++;
res = Math.max(res, area);
}
}
}
if (res == 0) {
return 1;
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 0) {
HashSet<Integer> neighbour = findNeighbour(grid, i, j);
if (neighbour.size() != 0) {
int b = 0;
for (int s : neighbour) {
b += indexAreaMap.get(s);
}
res = Math.max(res, b + 1);
} else {
continue;
}
}
}
}
return res;
}
private HashSet<Integer> findNeighbour(int[][] grid, int i, int j) {
HashSet<Integer> set = new HashSet<>();
if (inArea(grid, i - 1, j) && grid[i - 1][j] != 0) {
set.add(grid[i - 1][j]);
}
if (inArea(grid, i + 1, j) && grid[i + 1][j] != 0) {
set.add(grid[i + 1][j]);
}
if (inArea(grid, i, j - 1) && grid[i][j - 1] != 0) {
set.add(grid[i][j - 1]);
}
if (inArea(grid, i, j + 1) && grid[i][j + 1] != 0) {
set.add(grid[i][j + 1]);
}
return set;
}
private int dfs(int[][] grid, int index, int i, int j) {
if (!inArea(grid, i, j)) {
return 0;
}
if (grid[i][j] != 1) {
return 0;
}
grid[i][j] = index;
return 1 + dfs(grid, index, i - 1, j) + dfs(grid, index, i + 1, j) + dfs(grid, index, i, j - 1) + dfs(grid, index, i, j + 1);
}
private boolean inArea(int[][] grid, int i, int j) {
return i >= 0 && i < grid.length && j >= 0 && j < grid[0].length;
}
}
1905. 统计子岛屿
给你两个 m x n 的二进制矩阵 grid1 和 grid2 ,它们只包含 0 (表示水域)和 1 (表示陆地)。
一个 岛屿 是由 四个方向 (水平或者竖直)上相邻的 1 组成的区域。任何矩阵以外的区域都视为水域。
如果 grid2 的一个岛屿,被 grid1 的一个岛屿 完全 包含,也就是说 grid2 中该岛屿的每一个格子都被 grid1 中同一个岛屿完全包含,那么我们称 grid2 中
的这个岛屿为 子岛屿 。请你返回 grid2 中 子岛屿 的 数目 。
解题思路:
这道题的关键在于,如何快速判断子岛屿?肯定可以借助 Union Find 并查集算法 来判断,不过本文重点在 DFS 算法,就不展开并查集算法了。
什么情况下 grid2 中的一个岛屿 B 是 grid1 中的一个岛屿 A 的子岛?
当岛屿 B 中所有陆地在岛屿 A 中也是陆地的时候,岛屿 B 是岛屿 A 的子岛。
反过来说,如果岛屿 B 中存在一片陆地,在岛屿 A 的对应位置是海水,那么岛屿 B 就不是岛屿 A 的子岛。
那么,我们只要遍历 grid2 中的所有岛屿,把那些不可能是子岛的岛屿排除掉,剩下的就是子岛。
依据这个思路,可以直接写出下面的代码:
class Solution {
public int countSubIslands(int[][] grid1, int[][] grid2) {
int m = grid2.length, n = grid2[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid1[i][j] == 0 && grid2[i][j] == 1) {
dfs(grid2, i, j);
}
}
}
int count = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid2[i][j] == 1) {
dfs(grid2, i, j);
count++;
}
}
}
return count;
}
private void dfs(int[][] grid, int i, int j) {
if (!inArea(grid, i, j)) {
return;
}
if (grid[i][j] != 1) {
return;
}
grid[i][j] = 2;
dfs(grid, i - 1, j);
dfs(grid, i + 1, j);
dfs(grid, i, j + 1);
dfs(grid, i, j - 1);
}
private boolean inArea(int[][] grid, int i, int j) {
return i >= 0 && i < grid.length && j >= 0 && j < grid[0].length;
}
}
BFS
BFS 的核心思想应该不难理解的,就是把一些问题抽象成图,从一个点开始,向四周开始扩散。一般来说,我们写 BFS 算法都是用「队列」这种数据结构,每次将
一个节点周围的所有节点加入队列。
BFS 相对 DFS 的最主要的区别是:BFS 找到的路径一定是最短的,但代价就是空间复杂度可能比 DFS 大很多
至于为什么,我们后面介绍了框架就很容易看出来了。
先来看一下BFS的模板:
// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
Queue<Node> q; // 核心数据结构
Set<Node> visited; // 避免走回头路
q.offer(start); // 将起点加入队列
visited.add(start);
int step = 0; // 记录扩散的步数
while (q not empty) {
int sz = q.size();
/* 将当前队列中的所有节点向四周扩散 */
for (int i = 0; i < sz; i++) {
Node cur = q.poll();
/* 划重点:这里判断是否到达终点 */
if (cur is target)
return step;
/* 将 cur 的相邻节点加入队列 */
for (Node x : cur.adj()) {
if (x not in visited) {
q.offer(x);
visited.add(x);
}
}
}
/* 划重点:更新步数在这里 */
step++;
}
}
本文就由浅入深写两道 BFS 的典型题目,分别是「二叉树的最小高度」和「打开密码锁的最少步数」,手把手教你怎么写 BFS 算法。
二叉树的层序遍历的迭代写法就是典型的BFS。
让我们来看看层序遍历的迭代写法:
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) {
return res;
}
List<Integer> list = new ArrayList<>();
LinkedList<TreeNode> queue = new LinkedList<>();
queue.offer(root);
// while循环管从上到下的遍历
while(!queue.isEmpty()) {
// 注意这里不能直接写成 i < queue.size
// 因为遍历的同时也在向队列加元素,我们要确保遍历完一层,添加进结果集之后再处理新加进来的节点。
int size = queue.size();
// for循环管从左到右的遍历
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
list.add(node.val);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
res.add(list);
list = new ArrayList<>();
}
return res;
}
}
可以看到遍历完一个节点就会将这个节点的左右子节点放入队列中。之后继续出队然后遍历,循环往复。
662. 二叉树最大宽度⭐⭐⭐
给你一棵二叉树的根节点 root ,返回树的 最大宽度 。
树的 最大宽度 是所有层中最大的 宽度 。
每一层的 宽度 被定义为该层最左和最右的非空节点(即,两个端点)之间的长度。
将这个二叉树视作与满二叉树结构相同,两端点间会出现一些延伸到这一层的 null 节点,这些 null 节点也计入长度。
题目数据保证答案将会在 32 位 带符号整数范围内。
这道题的解题关键是要给二叉树节点按行进行编号,然后你就可以通过每一行的最左侧节点和最右侧节点的编号推算出这一行的宽度,进而算出最大宽度:

而且,这样编号还可以通过父节点的编号计算得出左右子节点的编号:
假设父节点的编号是 x,左子节点就是 2 * x,右子节点就是 2 * x + 1。
//层序遍历思路
class Solution {
// 记录节点和对应编号
class Pair {
TreeNode node;
int id;
public Pair( TreeNode node, int id) {
this.node = node;
this.id = id;
}
}
public int widthOfBinaryTree(TreeNode root) {
if (root == null) {
return 0;
}
// 记录最大的宽度
int maxWidth = 0;
// 标准 BFS 层序遍历算法
Queue<Pair> q = new LinkedList<>();
q.offer(new Pair(root, 1));
// 从上到下遍历整棵树
while (!q.isEmpty()) {
int sz = q.size();
int start = 0, end = 0;
// 从左到右遍历每一行
for (int i = 0; i < sz; i++) {
Pair cur = q.poll();
TreeNode curNode = cur.node;
int curId = cur.id;
// 记录当前行第一个和最后一个节点的编号
if (i == 0) {
start = curId;
}
if (i == sz - 1) {
end = curId;
}
// 左右子节点入队,同时记录对应节点的编号
if (curNode.left != null) {
q.offer(new Pair(curNode.left, curId * 2));
}
if (curNode.right != null) {
q.offer(new Pair(curNode.right, curId * 2 + 1));
}
}
// 用当前行的宽度更新最大宽度
maxWidth = Math.max(maxWidth, end - start + 1);
}
return maxWidth;
}
}
752. 打开转盘锁⭐⭐⭐
你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' 。
每个拨轮可以自由旋转:例如把 '9' 变为 '0','0' 变为 '9' 。每次旋转都只能旋转一个拨轮的一位数字。
锁的初始数字为 '0000' ,一个代表四个拨轮的数字的字符串。
列表 deadends 包含了一组死亡数字,一旦拨轮的数字和列表里的任何一个元素相同,这个锁将会被永久锁定,无法再被旋转。
字符串 target 代表可以解锁的数字,你需要给出解锁需要的最小旋转次数,如果无论如何不能解锁,返回 -1 。
class Solution {
int openLock(String[] deadends, String target) {
// 记录需要跳过的死亡密码
Set<String> deads = new HashSet<>();
for (String s : deadends) {
deads.add(s);
}
// 记录已经穷举过的密码,防止走回头路。
Set<String> visited = new HashSet<>();
Queue<String> q = new LinkedList<>();
// 从起点开始启动广度优先搜索
int step = 0;
// start
q.offer("0000");
visited.add("0000");
while (!q.isEmpty()) {
int sz = q.size();
/* 将当前队列中的所有节点向周围扩散 */
for (int i = 0; i < sz; i++) {
String cur = q.poll();
/* 判断是否到达终点 */
if (deads.contains(cur)) {
continue;
}
if (cur.equals(target)) {
return step;
}
/* 将一个节点的未遍历相邻节点加入队列 */
for (int j = 0; j < 4; j++) {
String up = plusOne(cur, j);
if (!visited.contains(up)) {
q.offer(up);
visited.add(up);
}
String down = minusOne(cur, j);
if (!visited.contains(down)) {
q.offer(down);
visited.add(down);
}
}
}
/* 在这里增加步数 */
step++;
}
// 如果穷举完都没找到目标密码,那就是找不到了
return -1;
}
// 将 s[j] 向上拨动一次
String plusOne(String s, int j) {
char[] ch = s.toCharArray();
if (ch[j] == '9') {
ch[j] = '0';
} else {
ch[j] += 1;
}
return new String(ch);
}
// 将 s[i] 向下拨动一次
String minusOne(String s, int j) {
char[] ch = s.toCharArray();
if (ch[j] == '0') {
ch[j] = '9';
} else {
ch[j] -= 1;
}
return new String(ch);
}
}
773. 滑动谜题(数字华容道)
在一个 2 x 3 的板上(board)有 5 块砖瓦,用数字 1~5 来表示, 以及一块空缺用 0 来表示。一次 移动 定义为选择 0 与一个相邻的数字(上下左右)进行交
换。最终当板 board 的结果是 [[1,2,3],[4,5,0]] 谜板被解开。给出一个谜板的初始状态 board ,返回最少可以通过多少次移动解开谜板,如果不能解开谜
板,则返回 -1 。
参考题解:https://labuladong.github.io/algo/4/31/112/
对于这种计算最小步数的问题,我们就要敏感地想到 BFS 算法。
这个题目转化成 BFS 问题是有一些技巧的,我们面临如下问题:
1、一般的 BFS 算法,是从一个起点 start 开始,向终点 target 进行寻路,但是拼图问题不是在寻路而是在不断交换数字这应该怎么转化成 BFS 算法问题呢?
2、即便这个问题能够转化成 BFS 问题,如何处理起点 start 和终点 target?它们都是数组哎,把数组放进队列,套 BFS 框架,想想就比较麻烦且低效。
首先回答第一个问题,BFS 算法并不只是一个寻路算法,而是一种暴力搜索算法,只要涉及暴力穷举的问题,BFS 就可以用,而且可以最快地找到答案。
你想想计算机怎么解决问题的?哪有那么多奇技淫巧,本质上就是把所有可行解暴力穷举出来,然后从中找到一个最优解罢了。
明白了这个道理,我们的问题就转化成了:如何穷举出 board 当前局面下可能衍生出的所有局面?这就简单了,看数字 0 的位置呗,和上下左右的数字进行交换
就行了:
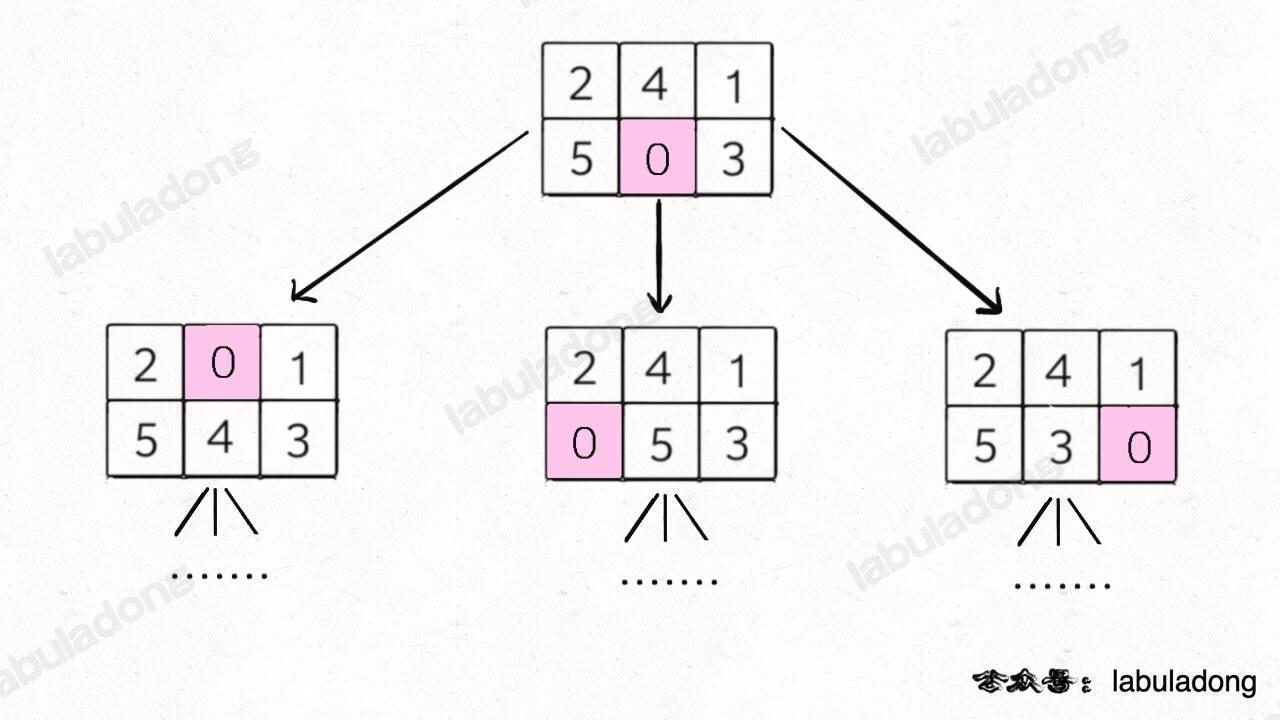
这样其实就是一个 BFS 问题,每次先找到数字 0,然后和周围的数字进行交换,形成新的局面加入队列…… 当第一次到达 target 时,就得到了赢得游戏的最少步
数。对于第二个问题,我们这里的 board 仅仅是 2x3 的二维数组,所以可以压缩成一个一维字符串。
其中比较有技巧性的点在于,二维数组有「上下左右」的概念,压缩成一维后,如何得到某一个索引上下左右的索引?
对于这道题,题目说输入的数组大小都是 2 x 3,所以我们可以直接手动写出来这个映射:
// 记录一维字符串的相邻索引
int[][] neighbor = new int[][]{
{1, 3},
{0, 4, 2},
{1, 5},
{0, 4},
{3, 1, 5},
{4, 2}
};
这个含义就是,在一维字符串中,索引 i 在二维数组中的的相邻索引为 neighbor[i]:
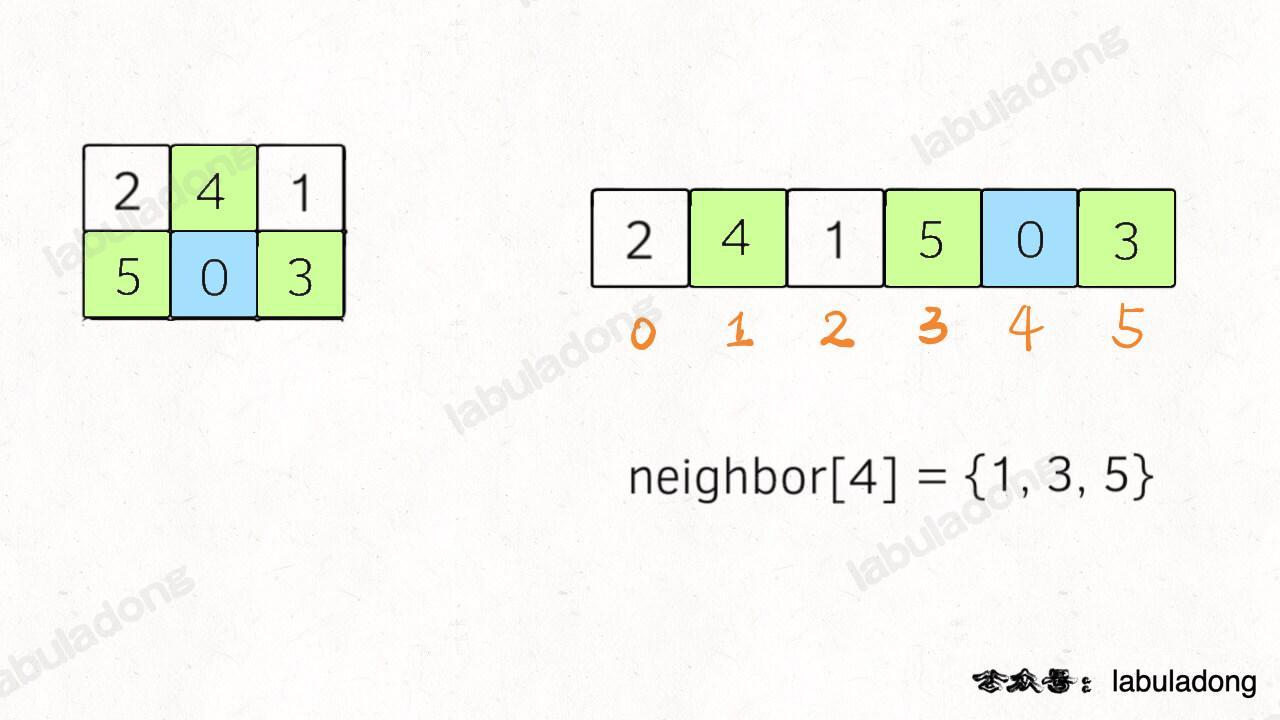
那么对于一个 m x n 的二维数组,手写它的一维索引映射肯定不现实了,如何用代码生成它的一维索引映射呢?
观察上图就能发现,如果二维数组中的某个元素 e 在一维数组中的索引为 i,那么 e 的左右相邻元素在一维数组中的索引就是 i - 1 和 i + 1,而 e 的上下
相邻元素在一维数组中的索引就是 i - n 和 i + n,其中 n 为二维数组的列数。
这样,对于 m x n 的二维数组,我们可以写一个函数来生成它的 neighbor 索引映射,篇幅所限,我这里就不写了。
至此,我们就把这个问题完全转化成标准的 BFS 问题了,借助前文 BFS 算法框架 的代码框架,直接就可以套出解法代码了:
class Solution {
public int slidingPuzzle(int[][] board) {
int m = 2, n = 3;
StringBuilder sb = new StringBuilder();
String target = "123450";
int step = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
sb.append(board[i][j]);
}
}
String start = sb.toString();
int[][] neighbor = new int[][] {
new int[]{1, 3},
new int[]{0, 2, 4},
new int[]{1, 5},
new int[]{0, 4},
new int[]{1, 3, 5},
new int[]{2, 4}
};
LinkedList<String> queue = new LinkedList<>();
HashSet<String> visited = new HashSet<>();
queue.offer(start);
visited.add(start);
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
String cur = queue.poll();
if (target.equals(cur)) {
return step;
}
int index = 0;
while (cur.charAt(index) != '0') {
index++;
}
for (int adj : neighbor[index]) {
String newRoad = swap(cur.toCharArray(), index, adj);
if (!visited.contains(newRoad)) {
queue.offer(newRoad);
visited.add(newRoad);
}
}
}
step++;
}
return -1;
}
public String swap(char[] chars, int i, int j) {
char temp = chars[i];
chars[i] = chars[j];
chars[j] = temp;
return new String(chars);
}
}
1306. 跳跃游戏 III
这里有一个非负整数数组 arr,你最开始位于该数组的起始下标 start 处。当你位于下标 i 处时,你可以跳到 i + arr[i] 或者 i - arr[i]。
请你判断自己是否能够跳到对应元素值为 0 的 任一 下标处。
注意,不管是什么情况下,你都无法跳到数组之外。
输入:arr = [4,2,3,0,3,1,2], start = 5
输出:true
解释:
到达值为 0 的下标 3 有以下可能方案:
下标 5 -> 下标 4 -> 下标 1 -> 下标 3
下标 5 -> 下标 6 -> 下标 4 -> 下标 1 -> 下标 3
class Solution {
public boolean canReach(int[] arr, int start) {
int n = arr.length;
// 避免走回头路
boolean[] visited = new boolean[n];
Queue<Integer> queue = new LinkedList<>();
// 将起点加入队列
queue.offer(start);
visited[start] = true;
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
int cur = queue.poll();
// 判断是否到达终点。
if (arr[cur] == 0) {
return true;
}
// cur可走的路径
if (cur - arr[cur] >= 0 && !visited[cur - arr[cur]]) {
queue.offer(cur - arr[cur]);
visited[cur - arr[cur]] = true;
}
if (cur + arr[cur] < n && !visited[cur + arr[cur]]) {
queue.offer(cur + arr[cur]);
visited[cur + arr[cur]] = true;
}
}
}
return false;
}
}
递归分治
38. 外观数列
给定一个正整数 n ,输出外观数列的第 n 项。
「外观数列」是一个整数序列,从数字 1 开始,序列中的每一项都是对前一项的描述。
你可以将其视作是由递归公式定义的数字字符串序列:
- countAndSay(1) = "1";
- countAndSay(n) 是对 countAndSay(n-1) 的描述,然后转换成另一个数字字符串。
111211211111221 第一项是数字 1 描述前一项,这个数是 1 即 “ 一 个 1 ”,记作 "11" 描述前一项,这个数是 11 即 “ 二 个 1 ” ,记作 "21" 描述前一项,这个数是 21 即 “ 一 个 2 + 一 个 1 ” ,记作 "1211" 描述前一项,这个数是 1211 即 “ 一 个 1 + 一 个 2 + 二 个 1 ” ,记作 "111221"
class Solution {
public String countAndSay(int n) {
// 递归出口
if (n == 1) {
return "1";
}
StringBuilder result = new StringBuilder();
// 先获取上一轮的结果,因为当前这一轮需要遍历上一轮结果得出。
String lastSeq = countAndSay(n - 1);
char lastNum = lastSeq.charAt(0);
int numCount = 0;
// 遍历上一轮结果
for (int i = 0; i < lastSeq.length(); i++) {
if (lastSeq.charAt(i) == lastNum) {
numCount++;
} else {
// 先记录次数
result.append(numCount);
// 再记录具体的值
result.append(lastNum);
// 更新
lastNum = lastSeq.charAt(i);
numCount = 1;
}
if (i == lastSeq.length() - 1) {
result.append(numCount);
result.append(lastNum);
}
}
return result.toString();
}
}
96. 不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
395. 至少有 K 个重复字符的最长子串
给你一个字符串 s 和一个整数 k ,请你找出 s 中的最长子串, 要求该子串中的每一字符出现次数都不少于 k 。返回这一子串的长度。
输入:s = "aaabb", k = 3
输出:3
解释:最长子串为 "aaa" ,其中 'a' 重复了 3 次。
class Solution {
public int longestSubstring(String s, int k) {
//如果字符串 s 的长度少于 k,那么一定不存在满足题意的子字符串,返回 0。
if (s.length() < k) {
return 0;
}
HashMap<Character, Integer> counter = new HashMap();
// 统计字符串s中每个字符出现的次数
for (int i = 0; i < s.length(); i++) {
counter.put(s.charAt(i), counter.getOrDefault(s.charAt(i), 0) + 1);
}
for (char c : counter.keySet()) {
// 如果 c 字符在字符串中出现的次数少于k次,
// 那么所有包含 c 字符的字串都不能满足题意,
// 应该在 s 的所有不包含 c 的子字符串中继续寻找结果。
// 把 s 按照 c 分割(分割后每个子串都不包含 c),得到很多子字符串 t。
// 下一步要求 t 作为源字符串的时候,它的最长的满足题意的子字符串长度
// (到现在为止,我们把大问题分割为了小问题(s → t))。
if (counter.get(c) < k) {
int res = 0;
for (String t : s.split(String.valueOf(c))) {
res = Math.max(res, longestSubstring(t, k));
}
return res;
}
}
return s.length();
}
}
139. 单词拆分(记忆化递归)💛
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。
参考题解:https://leetcode.cn/problems/word-break/solution/by-lfool-jjq9/
class Solution {
// n = s.length()
// 记录 [i...n-1] 是否可以拆分成单词
// 0 : 表示还未处理该子问题;1 : 表示可以;-1 : 表示不可以
private int[] memo;
public boolean wordBreak(String s, List<String> wordDict) {
memo = new int[s.length()];
return dfs(s, wordDict, 0);
}
private boolean dfs(String s, List<String> wordDict, int start) {
// 递归出口
if (start == s.length()) {
return true;
}
// 如果子问题已经处理过了,直接返回结果。
if (memo[start] != 0) {
return memo[start] == 1; // 1 or -1
}
for (int i = start; i < s.length(); i++) {
if (wordDict.contains(s.substring(start, i + 1))) {
boolean subRes = dfs(s, wordDict, i + 1);
if (subRes) {
// 说明 [start...n - 1] 是可以拆分成单词的。
memo[start] = 1;
return true;
}
}
}
// 已经完整遍历 [start...n-1] 都无法拆分。
memo[start] = -1;
return false;
}
}
410. 分割数组的最大值(记忆化递归)
给定一个非负整数数组 nums 和一个整数 m ,你需要将这个数组分成 m 个非空的连续子数组。
设计一个算法使得这 m 个子数组各自和的最大值最小。
输入:nums = [7,2,5,10,8], m = 2
输出:18
解释:
一共有四种方法将 nums 分割为 2 个子数组。
其中最好的方式是将其分为 [7,2,5] 和 [10,8] 。
因为此时这两个子数组各自的和的最大值为18,在所有情况中最小。
class Solution {
// 前缀和数组,因为数组和会超出int范围,因此用long
long[] s;
int n;
public int splitArray(int[] nums, int m) {
n = nums.length;
s = new long[n + 1];
for (int i = 1; i <= n; i++) {
s[i] = s[i - 1] + nums[i - 1];
}
return (int) helper(0, 0, m, new Long[n + 1][m + 1]);
}
// [i, n)是待划分的区域,j表示当前是第几个划分点,j个划分点能够划出j+1个区域。
public long helper(int i, int j, int m, Long[][] memo) {
if (memo[i][j] != null) {
return memo[i][j];
}
// 当j+1等于m时,划分完毕,直接返回当前区域的和。
if (j + 1 == m) {
return s[n] - s[i];
}
long min = Integer.MAX_VALUE;
// 穷尽所有划分点
for (int k = i; k < n; k++) {
// t是当前划分的组内和的最大值
long t = Math.max(s[k + 1] - s[i], helper(k + 1, j + 1, m, memo));
// min是所有可能划分的组内和的最大值的最小值
min = Math.min(t, min);
}
// 记忆
return memo[i][j] = min;
}
}
241. 为运算表达式设计优先级💛💛💛
给你一个由数字和运算符组成的字符串 expression ,按不同优先级组合数字和运算符,计算并返回所有可能组合的结果。你可以 按任意顺序 返回答案。
生成的测试用例满足其对应输出值符合 32 位整数范围,不同结果的数量不超过 10^4 。
输入:expression = "23-45"
输出:[-34,-14,-10,-10,10]
解释:
(2(3-(45))) = -34
((23)-(45)) = -14
((2(3-4))5) = -10
(2((3-4)5)) = -10
(((23)-4)5) = 10
参考题解:https://labuladong.gitee.io/algo/4/33/123/
class Solution {
HashMap<String, List<Integer>> memo = new HashMap<>();
public List<Integer> diffWaysToCompute(String input) {
// 避免重复计算
if (memo.containsKey(input)) {
return memo.get(input);
}
List<Integer> res = new LinkedList<>();
for (int i = 0; i < input.length(); i++) {
char c = input.charAt(i);
// 扫描算式 input 中的运算符。
if (c == '-' || c == '*' || c == '+') {
// 以运算符为中心,分割成两个字符串,分别递归计算。
List<Integer> left = diffWaysToCompute(input.substring(0, i));
List<Integer> right = diffWaysToCompute(input.substring(i + 1));
// 通过子问题的结果,合成原问题的结果。
for (int a : left) {
for (int b : right) {
if (c == '+') {
res.add(a + b);
} else if (c == '-') {
res.add(a - b);
} else if (c == '*') {
res.add(a * b);
}
}
}
}
}
// base case
// 如果 res 为空,说明算式是一个数字,没有运算符。表明什么时候可以开始治理了。
if (res.isEmpty()) {
res.add(Integer.parseInt(input));
}
// 将结果添加进备忘录。
memo.put(input, res);
return res;
}
}




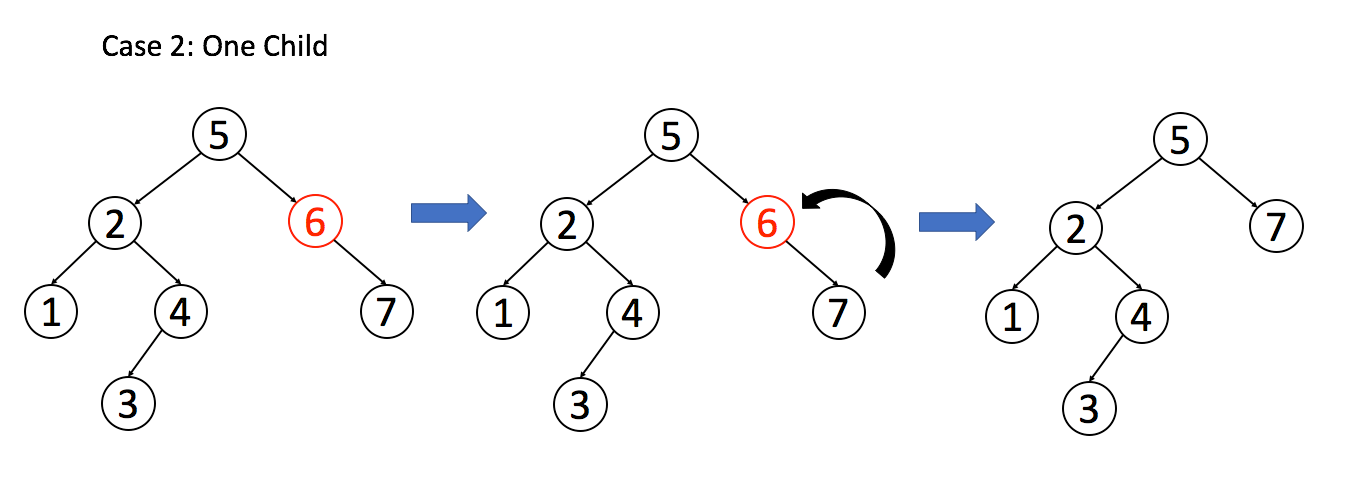
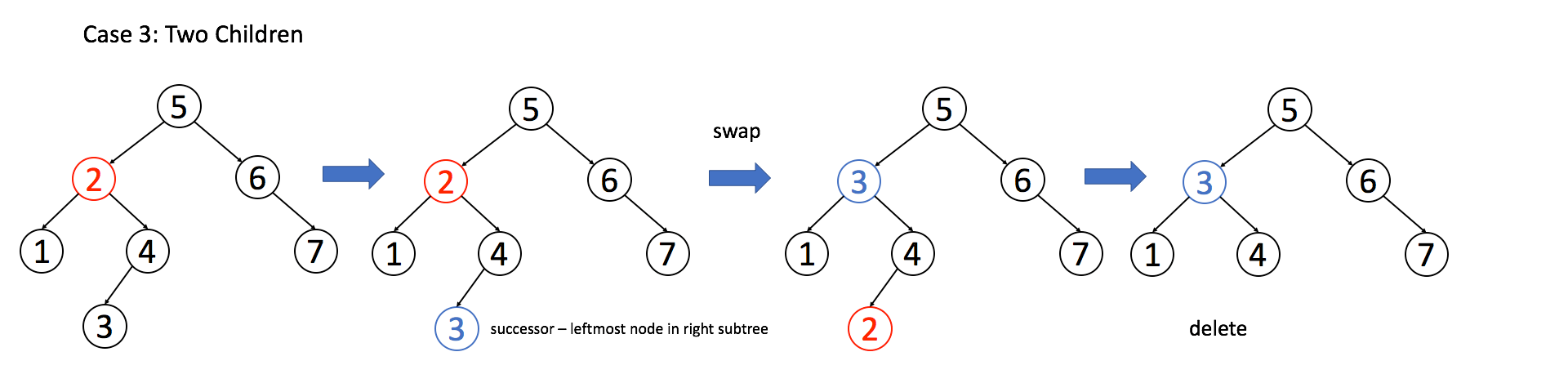

 浙公网安备 33010602011771号
浙公网安备 33010602011771号