符号化方法

解析组合试图从一个较为机械化的方式帮助我们将组合计数问题从模型直接转为生成函数。

—— $\text{EntropyIncreaser}$

解析组合为我们提供了一套能处理一系列组合结构计数和渐进估计的方法，分为解析和组合两个部分。
解析的部分主要讨论了如何近似生成函数的系数，而组合的部分则着眼于操作组合结构以便计数。符号化方法就是组合部分中操作组合结构的一种机械方法，通过描述组合结构来声明对应的生成函数。通过这种方式，我们就可以跳过转移方程，直接写出生成函数，也能够得到关于生成函数和组合意义的联系的更深刻理解。

阅读下文可能需要有基础的生成函数知识。也许是前置知识。

注意本文内容可能有疏漏或错误，如果读者发现敬请在评论区指出不足。

$1.$ 无标号体系
$2.$ 经典的无标号构造
$3.$ 有标号体系
$4.$ 经典的有标号构造
$5.$ 经典的有标号结构应用

$1.$ 无标号体系

$1.1$ 记号与定义

组合对象是满足某一性质的可数对象，例如二叉树、烯烃或字符串。组合类是一系列组合对象组成的可数集合。
下面将采用美术花体（\mathcal）大写字母表示一个组合类。

每个组合类 $\mathcal A$ 都定义了一个大小函数 $f: \mathcal A\to \mathbb N$，满足对任何 $k\in \mathbb N$ 只有有限个组合对象 $a\in \mathcal A$ 满足 $f(a) = k$。$f(a)$ 表示了组合对象 $a$ 的固有属性，可能是树高、节点数或串长等。常记 $f(a)$ 为 $\lvert a\rvert$（在某些需要指明组合类的场合下记作 $\lvert a \rvert_{\mathcal A}$）。
我们将 $a\in \mathcal A \text{ s.t. } \lvert a \rvert = n$ 的全体记作 $\mathcal A_n$，并以此构造一个计数序列 $A$，满足 $A[n] = \lvert \mathcal A_n\rvert$。
两个组合类 $\mathcal A, \mathcal B$ 在组合意义上同构记作 $\mathcal A = \mathcal B$ 或 $\mathcal A \cong \mathcal B$，但仅在 $\mathcal A$ 和 $\mathcal B$ 不同构时才用后一种记号。

我们在描述组合对象时只会关注我们需要的单一性质，这种抽象有助于我们理解下文中将不同对象组合为新的对象的操作。总的来说，我们忽视组合对象除了大小和组合结构外的所有信息，这样很多组合操作都可以被简单地映射在“并列”操作上。

一个组合类 $\mathcal A$ 的 $\text{OGF}$ 即其对应的计数序列 $A$ 的 $\text{OGF}$，为一个形式幂级数

\[A(z) = \sum_{i\ge 0} A[i] z^i \]

它也可以被等价地写作

\[A(z) = \sum_{a\in \mathcal A} z^{\lvert a \rvert} \]

我们称 $z^{\lvert a \rvert}$ 为 $a$ 的幂表示，这里的 $z$ 仍然只是占位元。

由以上内容不难验证组合类的笛卡尔积和 $\text{OGF}$ 的乘法 $\times$ 同构，集合不交并和 $\text{OGF}$ 的加法 $+$ 同构（处理了重复元素的加法会在下方重新定义）。
下面对集合的笛卡尔积也记作 $\times$，集合并也记作 $+$。

组合类都是由一些更本质的组合类构造出来的；一个构造是从一组组合类映射到一个组合类的函数。
当我们说一个构造可以被翻译为生成函数运算时，我们想要表达的就是这种组合类间的映射能和各组合类的生成函数间的运算对应。一个经典的例子是 $\exp$ 的组合意义；下文中还会有更多类似的例子。

下文中需要对某个组合类中元素进行去重操作，因此在这里先行引入等价关系和等价类。

对组合类 $\mathcal A$，其上的一个等价关系（用加粗大写字母/\textbf表示）$\textbf G$ 是 $\mathcal A \times \mathcal A$ 的一个子集 $\{(a, b) \mid a, b \in \mathcal A\}$，满足以下三个条件：

（自反性）$a \in \mathcal A \Rightarrow (a, a) \in \textbf G$;
（对称性）$(a, b) \in \textbf G, a \neq b \Rightarrow (b, a) \in \textbf G$;
（传递性）$(a, b), (b, c) \in \textbf G \Rightarrow (a, c) \in \textbf G$.

$a, b\in \mathcal A$ 在 $\textbf G$ 上等价当且仅当 $(a, b) \in \textbf G$，记作 $a\textbf G b$。

对于组合类 $\mathcal A$ 和等价关系 $\textbf G$，取 $\mathcal S \subseteq \mathcal A$，若 $\forall a, b \in \mathcal S, (a, b) \in \textbf G$，且 $\forall a \in \mathcal S, b \in \complement_{\mathcal A}\mathcal S, (a, b) \not \in \textbf G$，则我们称 $\mathcal S$ 是 $\textbf G$ 下的一个等价类。在实际讨论中，一个等价类中的组合对象大小一般相等。

对于组合类 $\mathcal A$ 和等价关系 $\textbf G$，定义 $\mathcal A / \textbf G$ 是一个新的组合类 $\bar{\mathcal A}$，满足 $\textbf G$ 下 $\mathcal A$ 的任意一个等价类在 $\bar{\mathcal A}$ 中有且仅有一个元素作为代表元；这里常取在某一性质（例如字典序）下最小元素。有时也定义新的组合类中的对象是原组合类中的等价类，即新组合类是“组合类的组合类”。

$1.2$ 基础无标号类

下面引入两种特殊的组合对象和对应的组合类。

我们记 $\epsilon$ 为中性对象（neutral object），对应的组合类记作 $\mathcal E = \{\epsilon \}$，称作中性类（neutral class）。
恒有 $\lvert \epsilon \rvert = 0$，因此有中性类的 $\text{OGF}$ $E(z) = 1$。
需要注意的是，两个中性对象 $\epsilon_1, \epsilon_2$ 可能不同。记一个下标为 $k$ 的中性对象 $\epsilon_k$ 对应的类为 $\mathcal E_k$。
我们有

\[\mathcal A \cong \mathcal E\times \mathcal A \cong \mathcal A\times \mathcal E \]

对于任意组合类 $\mathcal A$，规定 $\mathcal A^0 = \mathcal E$。但是由于组合意义，$\mathcal E$ 不能视作笛卡尔积的单位元。

定义了中性对象后，我们就可以定义不需要考虑交集的集合并了。由于集合论中需要满足集合内无重合元素，我们可以对两个类分别乘上不同的中性类，这样两个类中可能相同的对象在并集中也彼此不同。
我们定义两个类 $\mathcal A, \mathcal B$ 的集合并 $\mathcal A + \mathcal B$ 为

\[(\mathcal E_1 \times \mathcal A) \cup (\mathcal E_2 \times \mathcal B) \]

其中 $\cup$ 为集合的不交并。

我们记 $\bullet$ 为原子对象（atom object），对应的组合类记作 $\mathcal Z = \{\bullet \}$，称作原子类（atom class）。
恒有 $\lvert \bullet \rvert = 1$，因此有原子类的 $\text{OGF}$ $Z(z) = z$。
原子对象常用于合并数个组合对象，经典例子是作为树的根出现。

$1.3$ 例题

$\textbf{例 1}$：01 串

我们如何求得长度为 $n$ 的 01 串的个数？

设 01 串的组合类为 $\mathcal S$，我们要求的就是 $\lvert\mathcal S_n\rvert$。可以写出

\[\mathcal S = \{ \epsilon, \mathtt{0}, \mathtt{1}, \mathtt{00}, \mathtt{01}, \mathtt{10}, \mathtt{11}, \mathtt{000},\dots \} \]

对于某个 01 串，其要么为空串，要么是 $\mathtt{0},\mathtt{1}$ 接在另一个 01 串前面。可以写出

\[\mathcal S = \mathcal E + \{ \mathtt{0}, \mathtt{1} \}\times \mathcal S \]

翻译成生成函数就是 $S(z) = 1 + (z + z) S(z)$，也就能得到 $S(z) = \dfrac{1}{1 - 2z}$。答案即为 $[z^n]S(z) = 2^n$。

$\textbf{例 2}$：卡特兰数

我们如何构造长度为 $n$ 的生成函数？

卡特兰数有一个很经典的组合意义：$Cat(n)$ 是 $n$ 个点的二叉树个数。

对于一棵二叉树，它要么为空，要么形如 $左子树-根-右子树$。根可以视作 $\bullet$，两侧则又是二叉树。
假设二叉树的组合类为 $\mathcal C$，可以写出

\[\mathcal C = \mathcal E + \mathcal C \times \mathcal Z \times \mathcal C \]

翻译成生成函数就是 $C(z) = 1 + zC(z)^2$，这和我们先前得到的形式相同。

$2.$ 经典的无标号构造

$2.1$ 集合的 $\text{Sequence}$ 构造

$\text{Sequence}$ 构造生成了所有可能的有序组合。

我们定义

\[\text{SEQ}(\mathcal A) = \mathcal E + \mathcal A + \left(\mathcal A \times \mathcal A\right) + \left(\mathcal A \times \mathcal A \times \mathcal A\right) + \cdots \]

且要求 $\mathcal A_0 = \varnothing$，也就是 $\mathcal A$ 中没有大小为 $0$ 的对象。我们还可以将这构造生成的组合类写作

\[\text{SEQ}(\mathcal A) = \left\{\left(\beta_1, \beta_2, \dots, \beta_k\right) | k\ge 0, \beta_i \in \mathcal A\right\} \]

这映射翻译为生成函数即为

\[Q(A(z)) = 1 + A(z) + A^2(z) + A^3(z) + \cdots = \frac{1}{1 - A(z)} \]

其中 $Q$ 为 Pólya 准逆（quasi-inversion）。

$\textbf{例 1}$：写出 $\{\text{a}, \text{b}\}$ 的 $\text{Sequence}$ 构造：

\[\begin{aligned} &\text{SEQ}(\left\{\text{a}, \text{b}\right\}) \\ = \ & \quad \ \{\epsilon\} + \{\text{a}\} + \{\text{b}\} + \{\text{a} \text{b}\} + \{\text{b} \text{a}\} \\ & + \{\text{aaa}\} + \{\text{aab}\} + \{\text{aba}\} + \{\text{abb}\} \\ & + \{\text{baa}\} + \{\text{bab}\} + \{\text{bba}\} + \{\text{bbb}\} \\ & + \cdots \end{aligned}\]

$\textbf{例 2}$：有序有根树计数

我们可以使用 $\text{Sequence}$ 构造来定义有序有根树（不同儿子之间的顺序有意义的有根树）的计数。

设对应的组合类是 $\mathcal T$，我们可以用一个原子对象和自身的 $\text{Sequence}$ 描述自身，也就是

\[\mathcal T = \mathcal Z\times \text{SEQ}(\mathcal T) \]

翻译为生成函数就是

\[T(z) = \frac{z}{1 - T(z)} \]

从这里也可以看出，$T(z) = \dfrac{1 - \sqrt{1 - 4z}}{2}$，因此大小为 $n$ 的有序有根树的大小为移位的卡特兰数。

$2.2$ 集合的 $\text{Multiset}$ 构造

$\text{Multiset}$ 构造生成了所有可能的组合，但是不区分对象内部的元素的顺序。

我们仍然可以使用 $\text{Sequence}$ 构造描述 $\text{Multiset}$ 构造，但是由于顺序原因，我们可以递推解决，每次只拿出一个元素作 $\text{Sequence}$ 构造。假设 $\mathcal A = \left\{\alpha_0, \alpha_1, \dots, \alpha_k \right\}$，则可以递推地作 $\text{MSET}$ 构造如下：

\[\text{MSET}(\left\{\alpha_0, \alpha_1, \dots, \alpha_k \right\}) = \text{MSET}(\left\{\alpha_0, \alpha_1, \dots, \alpha_{k - 1} \right\})\times \text{SEQ}(\left\{\alpha_k\right\}) \]

即

\[\text{MSET}(\mathcal A) = \prod_{\alpha \in \mathcal A} \text{SEQ}(\{\alpha\}) \]

且要求 $\mathcal A_0 = \varnothing$。可以得到等价的

\[\text{MSET}(\mathcal A) = \text{SEQ}(\mathcal A) / \textbf R \]

其中 $(a_1, a_2, \dots, a_n)\textbf{R}(b_1, b_2, \dots, b_n)$ 当且仅当存在一个置换 $\sigma$，对于任意 $j$ 满足 $b_j = a_{\sigma(j)}$。

翻译为生成函数就是

\[\text{Exp}(A(z)) = \prod_{\alpha \in \mathcal A} \left( 1 - z^{\lvert\alpha\rvert} \right)^{-1} = \prod_{i\ge 1} (1 - z^i)^{- A[i]} \]

作 $\ln - \exp$ 可以得到

\[\begin{aligned} &\text{Exp}(A(z)) \\ = \ & \exp\left( \sum_{i\ge 1} - A[i] \ln(1 - z^i) \right) \\ = \ & \exp\left( \sum_{i\ge 1} - A[i] \sum_{j\ge 1} \frac{-z^{ij}}{j} \right) \\ = \ & \exp\left( \sum_{j\ge 1} \frac{1}{j} \sum_{i\ge 1} A[i] (z^{j})^{i} \right) \\ = \ & \exp\left( \sum_{j\ge 1} \frac{A(z^j)}{j} \right) \end{aligned}\]

其中 $\text{Exp}$ 被称作为 Pólya 指数，又称 Euler 变换。

$\textbf{例 1}$：整数的分拆

对每个 $1\le i \le 10^5$ 求 $f(i)$，其中 $f(k)$ 是将 $k$ 进行分拆的方案数。

设全体正整数类为 $\mathcal I$，可以发现

\[\mathcal I = \text{SEQ}_{\ge 1}(\mathcal Z) = \mathcal Z \times \text{SEQ}(\mathcal Z) \]

$\text{SEQ}_{\ge 1}$ 是有限制的构造，在下方讲到。当然求上面的东西对答案没啥帮助，我们可以直接构造 $I(z) = \sum_{i\ge 1} z^i$，所求的就是 $\text{MSET}(\mathcal I)$。

$\textbf{例 2}$：无标号无根树计数

我们能否对无标号无根树的计数构造生成函数？

假设无标号有根树的组合类是 $\mathcal T$，则可以写出

\[\mathcal T = \mathcal Z \times \text{MSET}(\mathcal T) \]

也就是

\[T(z) = z\times \text{Exp}(T(z)) \]

对于无根的情况，论文 The Number of Trees, Richard Otter 说明了无根树的 $\text{OGF}$ 是

\[T(z) - \frac{1}{2} T^2(z) + \frac{1}{2} T(z^2) \]

这点也可以通过对奇偶次项系数进行不同的讨论得到。这个数列即为 A55。

$\textbf{例 3}$：Pólya 指数的逆变换

我们能否根据 $\text{Exp}$ 的结构得到它的逆变换（不考虑常数项）？

记给定幂级数为 $F(z)$。我们需要求的就是一个序列 $A$，满足

\[F(z) = \prod_{i \ge 1} (1 - z^i)^{-A[i]} \]

两边取对数。得到

\[\begin{aligned} \ln F(z) & = \sum_{i \ge 1} - A[i] \ln(1 - z^i) \\ & = \sum_{i \ge 1} A[i] \sum_{j\ge 1} \frac{z^{ij}}{j} \\ & = \sum_{T\ge 1} z^{T} \sum_{d | T} \frac{d}{T} A[d] \end{aligned}\]

记 $\ln F(z)$ 为 $f$，可以发现

\[f[T] = \frac{1}{T}\sum_{d|T} d A[d] \]

作莫比乌斯反演得到

\[A[T] = \frac{1}{T} \sum_{d|T} df[d] \times\mu\left(\frac{T}{d}\right) \]

这就是逆运算的构造。

$2.3$ 集合的 $\text{Powerset}$ 构造

$\text{Powerset}$ 构造生成了所有可能的子集。

可以发现，对于每个元素我们都可以选或不选，这会导出两类不同的子集。因此我们可以递归地定义 $\text{PSET}$ 构造：

\[\text{PSET}(\left\{\alpha_0, \alpha_1, \dots, \alpha_k \right\}) = \text{PSET}(\left\{\alpha_0, \alpha_1, \dots, \alpha_{k - 1} \right\})\times (\mathcal E + \left\{\alpha_k\right\}) \]

可以写作

\[\text{PSET}(\mathcal A) \cong \prod_{\alpha \in \mathcal A} (\mathcal E + \{\alpha\}) \]

要求 $\mathcal A_0 = \varnothing$。

容易发现 $\text{PSET}(\mathcal A)\subset \text{MSET}(\mathcal A)$，因为 $\mathcal E + \{\alpha\} = \text{SEQ}_{k\le 1}(\{\alpha\})$。

翻译为生成函数就是

\[\overline{\text{Exp}}(A(z)) = \prod_{i\ge 1} (1 - z^i)^{A[i]} = \exp\left( \sum_{i \ge 1} (-1)^{i + 1} \frac{A(z^i)}{i} \right) \]

$2.4$ 集合的 $\text{Amplification}$ 构造

$\text{Amplification}$ 构造生成了所有可能的并列。

我们可以如此定义 $\text{AMP}$ 构造：

\[\text{AMP}(\mathcal A) = \bigcup_{\alpha \in \mathcal A} \text{SEQ}(\{ \alpha \}) \]

要求 $\mathcal A_0 = \varnothing$。

也就是说，任意多个 $\mathcal A$ 中的元素 $\alpha$ 自身的并列组成了 $\text{AMP}(\mathcal A)$。翻译成生成函数就是

\[\sum_{i\ge 0} A(z^i) \]

$2.5$ 集合的 $\text{Cycle}$ 构造

$\text{Cycle}$ 构造生成了所有可能的组合，但是不区分仅轮换不同的组合。

我们定义这个构造为

\[\text{CYC}(\mathcal A) = \left(\text{SEQ}(\mathcal A)\ \backslash\ \mathcal E\right) / \textbf S \]

其中 $\textbf S$ 为等价关系，$(a_1, a_2, \dots a_n) \textbf S(b_1, b_2, \dots, b_n)$ 当且仅当存在循环移位 $\tau$ 使得对于任意 $j$ 有 $b_j = a_{\tau(j)}$。

翻译为生成函数是

\[\text{Log}(A(z)) = \sum_{k\ge 1} \frac{\varphi(k)}{k} \ln \frac{1}{1 - A(z^k)} \]

$\text{Log}$ 被称作为 Pólya 对数。公式的证明可以参见 The Cycle Construction, P. Flajolet and M. Soria，这里不再展开。采用群论相关知识我们也可以获得相同的结果。

$\textbf{例 1}$：列举 $\text{CYC}(\{\text{a}, \text{b}\})$ 中长度为 $4$ 的对象。

它们分别为

\[\text{aaaa}, \text{aaab}, \text{aabb}, \text{abbb}, \text{bbbb}, \text{abab} \]

由于 $\text{aaab}\textbf S\text{aaba}\textbf S\text{abaa}\textbf S\text{baaa}, \text{aabb}\textbf S\text{abba}\textbf S\text{bbaa}\textbf S\text{baab}, \text{abbb}\textbf S\text{bbba}\textbf S\text{bbab}\textbf S\text{babb}, \text{abab}\textbf S\text{baba}$，这几个等价类都只有一个元素出现在 $\text{CYC}(\{\text{a}, \text{b}\})$ 中。

这里采用字典序最小的字符串作为代表。

$2.6$ 有限制的构造

对于上述构造，我们并没有限制每个对象组成部分的个数。
这里以 $\text{SEQ}$ 构造为例。我们若在 $\text{SEQ}$ 的下标加上作用于整数的谓词用于约束其组成部分的个数，如 $\text{SEQ}_{= k}, \text{SEQ}_{\ge k}, \text{SEQ}_{\in [1, k]}$，则表示构造出的等价类中每个对象的拆分中相同元素需要被下标上对应的谓词限制。常简写 $\text{SEQ}_{= k}$ 为 $\text{SEQ}_{k}$。

令一个构造 $\text{CONS}$ 为上述构造中的一种，并设 $\mathcal A = \text{CONS}_k(\mathcal B)$，则我们需要对 $\forall \alpha \in \mathcal A$ 有 $\alpha = \left\{(\beta_1, \beta_2, \dots, \beta_k) \mid \forall \beta_i \in \mathcal B \right\}$。

这种构造我们在先前已经充分接触过了，其翻译到生成函数上就是用新占位元来标识组成部分的个数。
组合意义上，我们定义 $\chi$ 函数作用于一个元素上标识其组成部分的个数，也就是它需要被对应的逻辑谓词限制。用在上面的例子上就是 $\chi(\alpha) = k$。

延续先前的记号，令

\[\mathcal A_{n, k} = \left\lvert \left\{ \alpha \in \mathcal A \mid \lvert\alpha\rvert = n, \chi(\alpha) = k \right\} \right\rvert \]

翻译为生成函数即为

\[A(z, t) = \sum_{n\ge 0} \sum_{k\ge 0} \mathcal A_{n, k} z^n t^k = \sum_{\alpha \in \mathcal A} z^{\lvert \alpha \rvert} t^{\chi(\alpha)} \]

我们只需要提取 $t^k$ 项系数即可得到对应的表达式。对应 $\text{SEQ}_k$ 就能得到

\[A(z, t) = \sum_{k\ge 0} B(z)^k t^z = \frac{1}{1 - tB(z)} \]

也就是 $A(z) = B(z)^k$。同样能得到 $\text{SEQ}_{\ge k}(\mathcal B)$ 能引出 $A(z) = \dfrac{B(z)^k}{1 - B(z)}$。

对于 $\text{MSET}_k$ 有

\[A(z, t) = \prod_{n\ge 0} (1 - tz^n)^{- B[n]} \]

这个得提取系数，得到

\[A(z) = [t^k] \exp \left( \sum_{i\ge 1} \frac{t^iB(z^i)}{i} \right) = \sum_{i\ge 0} \frac{1}{i!} [t^k]\left( \sum_{j\ge 1} \frac{t^j B(z^j)}{j} \right)^i \]

对于有限制的构造，没有要求 $\mathcal B_0 = \varnothing$。

常用的有限制构造

\[\begin{aligned} \text{PSET}_k(\mathcal A) &= [u^k]\exp\left( \sum_{i \ge 1}(-1)^{i + 1} \frac{u^i}{i}A(z^i) \right) \\ \text{MSET}_k(\mathcal A) &= [u^k]\exp\left( \sum_{i \ge 1} \frac{u^i}{i}A(z^i) \right) \\ \text{CYC}_k(\mathcal A) &= [u^k]\sum_{i\ge 1} \frac{\varphi(i)}{i} \log \frac{1}{1 - u^iA(z^i)} \end{aligned}\]

\[\begin{aligned} \text{PSET}_2(\mathcal A) &= \frac{A(z)^2}{2} - \frac{A(z^2)}{2} \\ \text{MSET}_2(\mathcal A) &= \frac{A(z)^2}{2} + \frac{A(z^2)}{2} \\ \text{CYC}_2(\mathcal A) &= \frac{A(z)^2}{2} + \frac{A(z^2)}{2} \end{aligned}\]

\[\begin{aligned} \text{PSET}_3(\mathcal A) &= \frac{A(z)^3}{6} - \frac{A(z)A(z^2)}{2} + \frac{A(z^3)}{3} \\ \text{MSET}_3(\mathcal A) &= \frac{A(z)^3}{6} + \frac{A(z)A(z^2)}{2} + \frac{A(z^3)}{3} \\ \text{CYC}_3(\mathcal A) &= \frac{A(z)^3}{3} + \frac{2A(z^3)}{3} \end{aligned}\]

\[\begin{aligned} \text{PSET}_4(\mathcal A) &= \frac{A(z)^4}{24} - \frac{A(z)^2A(z^2)}{4} + \frac{A(z)A(z^3)}{3} + \frac{A(z^2)^2}{8} - \frac{A(z^4)}{4} \\ \text{MSET}_4(\mathcal A) &= \frac{A(z)^4}{24} + \frac{A(z)^2A(z^2)}{4} + \frac{A(z)A(z^3)}{3} + \frac{A(z^2)^2}{8} + \frac{A(z^4)}{4} \\ \text{CYC}_4(\mathcal A) &= \frac{A(z)^4}{4} + \frac{A(z^2)^2}{4} + \frac{A(z^4)}{2} \end{aligned}\]

我们或许也可以通过 Pólya 定理导出结论。讲解可以看 HandWiki、Ency 或 x义x.

$\textbf{例 1}$：烷基计数

计数 $n$ 个节点的根节点度数不超过 $3$，其余节点度数不超过 $4$ 的无序有根树。

考虑我们把更小的满足条件的树的根连接到新根节点上时，会新建一条边，这也不会让原来的根的度数超过 $4$。因此假设满足条件的树的组合类为 $\mathcal T$，我们可以写出

\[\mathcal T = \mathcal Z \times \text{MSET}_{\le 3} (\mathcal T) \]

或者直接按能接上一棵空树来计数。假设 $\hat{\mathcal T} = \mathcal T + \mathcal E$，我们可以写出

\[\hat{\mathcal T} = \mathcal E + \mathcal Z \times \text{MSET}_3(\hat{\mathcal T}) \]

$\textbf{例 2}$：有序树的进一步探讨

承接 $2.1$ 例 $2$，我们限制每个节点子树的数量。

令 $\Omega\subseteq \mathbb N$ 为一个包含 $0$ 的集合。我们定义组合类 $\mathcal T^{\Omega}$，其中的对象被称作 $\Omega$ 树。一棵 $\Omega$ 树需要满足任意节点的儿子数量 $\omega \in \Omega$。在接下来的讨论中，常要用到 $\Omega$ 的特征函数

\[\phi(t) = \sum_{\omega \in \Omega} t^\omega \]

举几个例子。$\Omega = \{0, 2\}$ 对应的组合对象是满二叉树，其中每个节点要么没有儿子，要么有两个儿子。它的特征函数是 $\phi(t) = 1 + t^2$。$\Omega = \{0, 1, 2\}$ 对应的组合对象是一般的二叉树，特征函数是 $\phi(t) = 1 + t + t^2$；$\Omega = \{0, 3\}$ 对应的组合对象是三叉树，特征函数是 $\phi(t) = 1 + t^3$。对于一般的树有 $\Omega = \mathbb N$，特征函数是 $\phi(t) = (1 - t)^{-1}$。

我们可以通过 $\Omega$ 的特征函数 $\phi$ 递归定义 $\mathcal T^{\Omega}$ 的 $\text{OGF}$ $T^{\Omega}(z)$：

\[T^{\Omega}(z) = z\times \phi\left(T^{\Omega}(z)\right) \]

这形式的证明需要从 $\text{SEQ}$ 构造着手。一个节点限制儿子的数量后子树的选择方案可以施 $\text{SEQ}_{\in \Omega}$ 构造，对组合类我们能写出 $\mathcal T^{\Omega} = \mathcal Z\times \text{SEQ}_{\in \Omega} (\mathcal T^{\Omega})$。之前的讨论可以推广到这里，这种构造翻译成生成函数就是复合 $\phi$，也就是 $T^{\Omega}(z) = z\times \phi\left(T^{\Omega}(z)\right)$。

上面的形式启发我们通过拉格朗日反演提取系数。我们知道 $\dfrac{T^{\Omega}(z)}{\phi\left(T^{\Omega}(z)\right)} = z$，这就有 $\left(T^{\Omega}(z)\right)^{\langle -1\rangle} = \dfrac{z}{\phi(z)}$。可以得到

\[\mathcal T^{\Omega}_n = [z^n] T^{\Omega}(z) = \frac{1}{n}[z^{n - 1}] \phi(z)^n \]

如上的思路在 $\Omega$ 为多重集时自然成立。例如，$\Omega = \{0, 1, 1, 3\}$ 给出了一种一叉-三叉树，这类树可以有两种一叉节点，分别染了不同的颜色；这集合的特征函数就是 $\phi(z) = 1 + 2z + z^3$。

由上面的讨论不难看出，如果 $\Omega$ 包含了 $r$ 个不同的元素，则对 $\Omega$ 树的计数可以用一个 $r - 1$ 重的二项式系数求和表示。

我们也可以用这种方法计数 $k$ 阶 $\Omega$ 树森林，其组合类定义为 $\mathcal F = \text{SEQ}_k(\mathcal T^{\Omega})$。关注生成函数能得到 $F(z) = T^{\Omega}(z)^k$。
同样应用拉格朗日反演可以得到

\[[z^n] F(z) = [z^n]T(z)^k = \frac{k}{n} [z^{n - k}] \phi(z)^n \]

当 $\Omega = \mathbb N$ 时，我们有 $k$ 阶一般树森林的计数为

\[[z^n] \left(\frac{1 - \sqrt{1 - 4z}}{2}\right)^k = \frac{k}{n}\binom{2n - k - 1}{n - 1} \]

系数对应的数列又被称为 ballot numbers。

当 $\Omega = \{0, 1, 2\}$ 时，令 $\mathcal M$ 为对应的一般二叉树的组合类，不难写出 $\mathcal M = \mathcal Z\times \text{SEQ}_{\le 2}(\mathcal M)$，也就能得到

\[M(z) = z\left(1 + M(z) + M^2(z)\right)\quad \Rightarrow \quad M(z) = \frac{1 - z - \sqrt{1 - 2z - 3z^2}}{2z} \]

可以用拉格朗日反演导出

\[[z^n]M(z) = \frac{1}{n} \sum_{k > 0} \binom{n}{k} \binom{n - k}{k - 1} \]

系数对应的数列（移位）又被称为 Motzkin numbers。

可能的例题：P7592 数树

$\textbf{例 3}$：被括号包含（bracketed）

这个问题被论文 Vier combinatorische Probleme, E. Schröder 系统地阐述后广为人知，它也是这篇论文中的第二个问题。
我们需要计数的是 $n$ 个相同的字母 $x$ 有多少种被括号包含的合法方案。合法方案是递归地定义的：

$x$ 本身是合法方案。
若 $\sigma_1, \sigma_2, \dots, \sigma_k$ 分别是合法方案，且 $k \ge 2$，则 $(\sigma_1 \sigma_2 \cdots \sigma_k)$ 是合法的，也就是并列后在最外层加一对括号。

例如，$(((xx)x(xxx))((xx)(xx)x))$ 是合法的，$((((x)(x))))$ 就不是。

我们令 $\mathcal S$ 表示合法方案对应的组合类，大小函数表示一个方案中 $x$ 的个数。上面的递归定义可以被形式化地表示为

\[\mathcal S = \mathcal Z + \text{SEQ}_{\ge 2}(\mathcal S) \]

翻译得到

\[S(z) = z + \frac{S(z)^2}{1 - S(z)} \]

考虑一个合法序列和一棵树的关系。可以发现，每个 $x$ 代表的就是这棵树的叶子节点，而一对括号代表了树的内部节点，我们需要保证内部节点的度数 $\ge 2$。叶子节点在这里对大小函数有贡献，内部节点则没有。
注意这里树的形式和例 $2$ 中描述的形式不同，大小函数的定义也不同，无法直接应用上面的构造。但是拉格朗日反演仍然可以应用，这里有

\[S^{\langle -1\rangle}(z) = \frac{x(1 - 2x)}{1-x} \]

提取 $z^n$ 项系数可以得到

\[\frac{1}{n} [z^{n -1}]\left(\frac{1-x}{1 -2x}\right)^{n} = \frac{(-1)^{n - 1}}{n} \sum_{k\ge 0} (-2)^k \binom{n}{k + 1}\binom{n + k - 1}{k} \]

这个其实微分有限，化成组合数形式也只是为了得到新的组合意义。

系数对应的数列是 A1003。

$2.7$ 隐式构造

在很多情况下，我们会见到隐式构造的组合类 $\mathcal X$，它作为一个映射的原像出现，而像已经被定义了。我们希望刻画这种组合类，并将他显式地放在像的位置。这就促使我们在组合类运算中定义逆。

我们举几个例子，其中 $\mathcal A, \mathcal B$ 已知，$\mathcal X$ 是新定义的：

\[\mathcal A = \mathcal B + \mathcal X \quad \mathcal A = \mathcal B \times \mathcal X \quad \mathcal A = \text{SEQ}(\mathcal X) \quad \mathcal A = \text{MSET}(\mathcal X) \]

这里用生成函数的语言更容易定义逆。分别地，我们有

\[X(z) = A(z) - B(z) \quad X(z) = \frac{A(z)}{B(z)} \quad X(z) = 1 - \frac{1}{A(z)}\quad X(z) = \sum_{k\ge 1} \frac{\mu(k)}{k} \ln A(z^k) \]

$\text{MSET}$ 的逆的形式已经在 $2.2$ 例 $3$ 讨论了。

通过组合类间关系隐式构造的组合类被称为隐式结构（implicit structures）。

$\textbf{例 1}$：排列的连续段分解

一个排列 $\sigma = \sigma_1 \sigma_2 \cdots \sigma_n$ 是可分解的，当且仅当其下标可以被分割为大于一个不交的区间 $[l_i, r_i] = \{k \mid k\in \mathbb N \land l_i\le k \le r_i \}$，满足

这些区间的并集是 $[1,n] = \{k \mid k\in \mathbb N \land 1\le k \le n \}$；
对任何一个区间 $[l,r]$，$\forall i \in [l, r], \exist j\in [l, r], \sigma_i = j$；
对任意两个区间 $[l_i, r_i], [l_j, r_j]$ 满足 $i < j$，有 $\forall x \in [l_i, r_i], \forall y \in [l_j, r_j], \sigma_x < \sigma_y$；
区间数量极大。

举例来说，$\sigma = \{2,5,4,1,3,6,8,10,7,9\}$ 的分解就是 $[1, 5], [6, 6], [7, 10]$，用图像表示就是

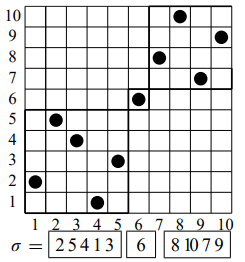
我们称无法执行上述操作的排列是不可分解的排列，例如 $\{2,4,1,3\}, \{5,4,3,2,1\}$。现在请构造不可分解的排列的组合类 $\mathcal I$。

我们取出排列 $\sigma$ 的分解中的一段 $[l,r]$ 来观察。不难发现，排列 $\{\sigma_l - l + 1, \sigma_{l+1} - l + 1, \dots, \sigma_r - l + 1 \}$ 是一个新的 $1\sim r - l + 1$ 的排列，且这个排列是不可再分解的。我们如果只关注排列的大小，则一个可分解的排列是一系列不可分解的排列的并列。

假设任意排列的组合类是 $\mathcal P$，则我们能得到

\[\mathcal P = \text{SEQ}(\mathcal I) \]

这隐式定义了 $\mathcal I$，可以写出

\[I(z) = 1 - \frac{1}{P(z)} \qquad \text{where} \ P(z) = \sum_{n\ge 0}n ! z^n \]

系数对应的数列是 A3319。

$\textbf{例 2}$：系数在有限域内的素多项式

我们固定一个质数 $p$，下面所有系数间的运算都在模 $p$ 数域 $\mathbb F_p$ 内运算。记多项式环 $\mathbb F_p[x]$ 是系数在 $\mathbb F_p$ 内的多项式的全体组成的环。

我们在这里讨论的是首一多项式，即最高次项系数为 $1$ 的多项式。记 $\mathbb F_p[x]$ 集合内的首一多项式组成了组合类 $\mathcal P$，大小函数定义为多项式最高次项。记 $\mathcal A = \mathbb F_p$。由于一个多项式可以由它的系数唯一确定，我们可以将它视作由 $\mathcal A$ 内对象组成的序列，因此有

\[\mathcal P = \text{SEQ}(\mathcal A) \quad \Rightarrow \quad P(z) = \frac{1}{1 - pz} \]

这也能得到有 $p^n$ 个最高次项为 $x^n$ 的首一多项式。

众所周知，多项式域 $\mathbb F_p[x]$ 上可以作欧几里得法求最大公因子，因此多项式域是 $\text{UFD}$。我们称没有除常数外的因子的多项式是素多项式，是不可分解的。举例来说，在 $\mathbb F_3[x]$ 上有

\[x^{10} + x^8 + 1 = (x + 1)^2(x + 2)^2 (x^6 + 2x^2 + 1) \]

我们令 $\mathcal I$ 为素多项式对应的组合类。唯一分解性质说明，$\mathcal P$ 在组合意义上和 $\mathcal I$ 的 $\text{Multiset}$ 构造同构，也就是

\[\mathcal P\cong \text{MSET}(\mathcal I) \]

这样我们就能写出

\[P(z) = \exp\left( \sum_{j\ge 1} \frac{I(z^j)}{j} \right) \]

我们也自然能通过上面的方法以及提取系数得到

\[I(z) = \sum_{k\ge 1} \frac{\mu(k)}{k} \ln \frac{1}{1 - pz^k}\quad \mathcal I_n = \frac{1}{n} \sum_{d | n} \mu(d) {p}^{n / d} \]

特别的，$\mathcal I_n = O(p^n / n)$。这个结论已经被高斯知晓。因此 $n$ 度的多项式中任选一个多项式是素多项式的概率为 $1/n$。

$3.$ 有标号体系

$3.1$ 概述

有标号体系是无标号体系的自然拓展，大部分组合对象的性质都可以自然地引入有标号体系中。

有标号体系和无标号体系最大的区别在于，有标号体系所关注的对象都有着两两不同的标号，彼此可以区分。不失一般性地，我们将标号集合视作正整数集合。举例来说，一个排列可以被视作一系列两两不同正整数依次排开，而循环分解将这排列视作循环有向图的组合，图的每个顶点都有着正整数标号。

有标号体系内的操作基于一类特殊的乘法：有标号乘（labelled product）。它是对无标号体系中笛卡尔积的自然模拟。
同样的，我们也需要得到对无标号体系中 $\text{OGF}$ 的有标号模拟，这就是指数生成函数，简称 $\text{EGF}$。在下面的叙述中我们可以看到，$\text{EGF}$ 可以很好地描述计数序列。
新的构造使得我们能关注更多的结构，特别是在有顺序的性质上。

$3.2$ 记号与定义

我们所处理的对象和无标号体系一样，是有限的组合类与组合对象。不同的是，我们现在处理的组合对象是有标签的。每个组合对象都[有一种独特的颜色/被分配到一个正整数标号]，以保证组合对象是两两不同的。

一个大小为 $n$ 的弱标号对象是一种有 $n$ 个部分的离散结构，其 $n$ 个部分分别有一个标号，这些标号组成了一个大小为 $n$ 的整数集。我们称满足这条件的对象是弱标号的。等价地，可以说每个部分都有标号，这种叙述隐含了标号是 $\in \mathbb Z$ 的彼此不同的数。一个大小为 $n$ 的有标号（又称强标号，一般在需要区分弱标号对象的语境下使用）对象需要是弱标号的，且其标号组成的集合是整数区间 $[1, n] = \{x\mid x\in \mathbb N, 1\le x\le n\}$。一个例子是一张有 $n$ 个节点的图，它的一个部分是一个带标号节点。
一个有标号类是一个由有标号的组合对象组成的组合类，这里把 $1.$ 中介绍过的无标号的组合类称作无标号类，以示区分。对有标号类的记号仍然沿用美术花体（\mathcal）大写字母，其中的一个有标号对象常记作对应的小写字母/希腊字母，对应的生成函数用对应的一般字体大写字母记。有标号类也是一个组合类，大小函数、计数序列和同构等定义与 $1.$ 中介绍的无标号类相同。

一个有标号类 $\mathcal A$ 的 $\text{EGF}$ 可以用它的计数序列 $A[n]$ 或其中元素表示，写作

\[A(z) = \sum_{i\ge 0} A[i] \frac{z^i}{i!} = \sum_{\alpha \in \mathcal A} \frac{z^{\lvert \alpha \rvert}}{\lvert \alpha \rvert!} \]

这里的 $z$ 是用于标记组合对象大小的占位元。

这里作一下关于 $\text{EGF}$ 的提取系数的声明。提取系数需要满足 $A[n] = n!\times [z^n]A(z)$，也就是 $[z^n]A(z) = A[n]/n!$。

$3.3$ 基础有标号类与操作

在无标号体系中，我们已经见到了中性类和原子类发挥的作用，不妨在有标号体系中也定义这样的结构。

我们记 $\epsilon$ 为中性对象（neutral object），对应的组合类记作 $\mathcal E = \{\epsilon \}$，称作中性类（neutral class）。
恒有 $\lvert \epsilon \rvert = 0$，因此有中性类的 $\text{EGF}$ $E(z) = 1$。
我们记 $①$ 为原子对象（atom object），对应的组合类记作 $\mathcal Z = \{① \}$，称作原子类（atom class）。我们令原子对象中唯一的元素标号恒为 $1$，这使得原子对象是强标号的。
恒有 $\lvert① \rvert = 1$，因此有原子类的 $\text{EGF}$ $Z(z) = z$。

有标号类的集合并可以类似无标号类的集合并一样定义，这里也记作 $+$。$\mathcal A + \mathcal B$ 翻译到生成函数上就是 $A(z) + B(z)$。

而有标号类的乘法不好得到良定义，这是由于笛卡尔积的结构可能导出非良标号对象，也就是两个有标号对象可能存在标号重叠的情况。我们不采用笛卡尔积，而是定义新的运算：有标号乘法，这运算可以自然地翻译为 $\text{EGF}$ 的乘法。记 $\mathcal A$ 与 $\mathcal B$ 的有标号乘法为 $\mathcal A \times \mathcal B$，它翻译到生成函数上是 $A(z)\times B(z)$。注意这里没有定义 $\mathcal A,\mathcal B$ 的笛卡尔积，我们也不使用 $\star$ 代替 $\times$。

首先介绍二项式卷积，也就是 $\text{EGF}$ 在做乘法运算时系数的映射结构。假设 $F(z), G(z), H(z)$ 分别是序列 $f, g, h$ 的 $\text{EGF}$，且 $F(z) = G(z)\times H(z)$，能发现它们的系数满足

\[\frac{f[n]}{n!} = \sum_{k = 0}^n \frac{g[k]}{k!} \times \frac{h[n - k]}{(n - k)!} \quad \Rightarrow \quad f[n] = \sum_{k = 0}^{n}\binom{n}{k} g[k] \times h[n - k] \]

同样的，如果我们有 $F(z) = G_1(z)\times G_2(z)\times\cdots\times G_r(z)$，则

\[f[n] = \sum_{n_1 + n_2 + \cdots n_r = n} \binom{n}{n_1, n_2, \dots, n_r} g_1[n_1] \times g_2[n_2]\times\cdots\times g_r[n_r] \]

这里的系数是多项式系数，有

\[\binom{n}{n_1, n_2, \dots, n_r} = \frac{n!}{n_1!\times n_2!\times \cdots \times n_r!} \]

这种结构对我们下面的讨论很有帮助，是 $\text{EGF}$ 应用的核心所在。

我们接下来要讨论的是重标号操作。由于我们需要让两个强标号对象合并后仍然是强标号的，我们需要进行重标号操作，这种操作要求新的标号的大小关系中保留原标号之间的大小关系。下面列出的两种重标号方式是重要的：

减缩。
对于一个大小为 $n$ 的弱标号结构，减缩操作将每个点的标号映射到整数区间 $[1, n]$ 内，保留了原标号的大小关系，相当于作了离散化。我们记对结构 $\alpha$ 做减缩操作得到 $\rho(\alpha)$。
举例来说，序列 $\langle 7, 3, 9, 2 \rangle$ 减缩得到 $\langle 3, 2, 4, 1 \rangle$。
增扩。
定义该操作需要一个增扩函数 $e : [1, n]\to \mathbb Z$，满足 $\forall i\in [1, n], e(i) > i$。对于一个强标号对象 $\alpha$，定义它增扩后得到一个弱标号对象 $\hat\alpha$，$\alpha$ 中标号为 $k$ 的部分在 $\hat\alpha$ 中标号为 $e(k)$。我们记对结构 $\alpha$ 做增扩操作得到 $e(\alpha)$。
举例来说，序列 $\langle 3, 2, 4, 1 \rangle$ 增扩可以得到 $\langle 33, 22, 44, 11 \rangle$ 或 $\langle 7, 3, 9, 2 \rangle$。

我们可以通过这些操作设计出一种适于有标号类的乘法，其最初由 D. Foata 提出，取名为 partitional product。有标号乘法的思路就是对合并后的部分进行重标号，以避免出现同一个标号出现多次。

我们取两个有标号对象 $\beta \in \mathcal B$ 和 $\gamma \in \mathcal C$，我们定义这两个对象的有标号乘法（简称乘法）记作 $\beta \times \gamma$，定义为一个集合，其包含所有由 $(\beta, \gamma)$ 生成的强标号的有序对 $(\beta', \gamma ')$。具体地，我们定义

\[\beta\times \gamma = \{ (\beta', \gamma) \mid (\beta', \gamma ')强标号, \rho(\beta') = \beta, \rho(\gamma') = \gamma \} \]

这个定义同样可以通过增扩导出，不再赘述。

注意到有标号乘积导出的构造中每个对象都是强标号的。假设 $\beta, \gamma$ 都是强标号的，大小分别为 $n_1, n_2$，则分配标号的方案总共有 $\dbinom{n_1 + n_2}{n_1}$ 种，也就是说

\[\lvert\beta\times \gamma\rvert = \dbinom{n_1 + n_2}{n_1} \]

随后我们就能对有标号类自然地定义有标号乘法了。

设 $\mathcal B, \mathcal C$ 是两个有标号类，则 $\mathcal B$ 和 $\mathcal C$ 的有标号乘法记作 $\mathcal B \times \mathcal C$，定义为

\[\mathcal B \times \mathcal C = \bigcup_{\beta \in \mathcal B, \gamma \in \mathcal C} \beta\times \gamma \]

随后我们可以自然地描述计数序列的关系了。假设 $\mathcal A = \mathcal B \times \mathcal C$，则我们能知道

\[\mathcal A_n = \bigcup_{|\beta| + |\gamma| = n} \beta\times \gamma\quad\Rightarrow\quad A[n] = \sum_{i + j = n} \binom{n}{i} B[i]\times C[j] \]

可以发现这转移和 $\text{EGF}$ 的乘法同构。因此我们构造出了一种有意义的有标号乘法，使得 $\text{EGF}$ 可以用来描述组合类的计数序列。

通过这个构造，我们就可以构造有标号集合、有标号序列和有标号循环了，方法和无标号的构造法类似。在这过程中我们也会注意可容许性。

$4.$ 经典的有标号构造

$4.1$ 有标号 $\text{Sequence}$ 构造

有标号 $\text{Sequence}$ 构造生成了所有可能的有标号序列。

一个有标号类 $\mathcal B$ 的 $k$ 次（有标号）幂被定义为 $\mathcal A = \mathcal B\times \mathcal B\times \cdots \times \mathcal B$，这里有 $k$ 个 $\mathcal B$ 作乘法。翻译为生成函数为 $A(z) = B(z)^k$。
$\mathcal B$ 的 $k$ 次（有标号）幂记作 $\text{SEQ}_k(\mathcal B)$。

我们定义

\[\text{SEQ}(\mathcal A) = \mathcal E + \mathcal A + \mathcal A\times \mathcal A + \mathcal A \times \mathcal A\times \mathcal A + \cdots = \bigcup_{k\ge 0} \text{SEQ}_k(\mathcal A) \]

记 $\mathcal B = \text{SEQ}(\mathcal A)$。翻译为生成函数即为

\[B(z) = 1 + A(z) + A(z)^2 + A(z)^3 + \cdots = \frac{1}{1 - A(z)} \]

这里仍然需要 $\mathcal A_0 \neq \varnothing$。

$4.2$ 有标号 $\text{Set}$ 构造

有标号 $\text{Set}$ 构造生成了所有可能的有标号序列，但是不区分组成对象的元素的顺序。

由有标号类 $\mathcal B$ 中对象作为元素的大小为 $k$ 的集合的全体就是有标号类 $\mathcal B$ 的 $\text{Set}_k$ 构造。它是无标号类中 $\text{Multiset}, \text{Powerset}$ 构造的模拟，定义为 $\text{SET}_k(\mathcal B) = \text{SEQ}_k(\mathcal B) / \textbf R$，其中 $(a_1, a_2, \dots, a_n)\textbf{R}(b_1, b_2, \dots, b_n)$ 当且仅当存在一个置换 $\sigma$，对于任意 $j$ 满足 $b_j = a_{\sigma(j)}$。
由有标号类 $\mathcal B$ 中对象作为元素的集合的全体就是有标号类 $\mathcal B$ 的 $\text{Set}$ 构造。我们定义

\[\text{SET}(\mathcal A) = \bigcup_{k\ge 0} \text{SET}_k(\mathcal A) \]

对于一个有标号类，有标号 $\text{Set}_k$ 构造中的一个元素对应着有标号 $\text{Sequence}$ 构造中的 $k!$ 个元素，这可以通过计数置换得到。因此可以将这构造翻译为生成函数：

记 $\mathcal B = \text{SET}_k(\mathcal A)$。$\text{Set}_k$ 构造翻译为生成函数即为

\[B(z) = \frac{1}{k!}A(z)^k \]

记 $\mathcal B = \text{SET}(\mathcal A)$。$\text{Set}$ 构造翻译为生成函数即为

\[B(z) = \sum_{k\ge 0} \frac{1}{k!}A(z)^k = \exp A(z) \]

这里仍然需要 $\mathcal A_0 \neq \varnothing$。

注意到无标号 $\text{Powerset}$ 构造和无标号 $\text{Multiset}$ 构造在带标号后同构，$\text{Powerset}$ 构造可以并入，统称为有标号 $\text{Set}$ 构造。

$4.3$ 有标号 $\text{Cycle}$ 构造

$\text{Cycle}$ 构造生成了所有可能的有标号序列，但是不区分仅轮换不同的序列。

有标号 $\text{Cycle}$ 构造是无标号类中 $\text{Cycle}$ 构造的模拟，定义为 $\text{CYC}_k(\mathcal B) = \text{SEQ}_k(\mathcal B) / \textbf S$，其中 $(a_1, a_2, \dots a_n) \textbf S(b_1, b_2, \dots, b_n)$ 当且仅当存在循环移位 $\tau$ 使得对于任意 $j$ 有 $b_j = a_{\tau(j)}$。
同上地定义 $\text{CYC}(\mathcal B) = \sum_{k\ge 0}\text{CYC}_k(\mathcal B)$。

可以发现，$\text{CYC}_k(\mathcal B)$ 中任意一个对象在 $\text{SEQ}_k(\mathcal B)$ 中出现了恰好 $k$ 次，因为每个对象都可以旋转 $k$ 次。因此可以将这构造翻译为生成函数：

记 $\mathcal B = \text{CYC}_k(\mathcal A)$。$\text{Cycle}_k$ 构造翻译为生成函数即为

\[B(z) = \frac{1}{k}A(z)^k \]

记 $\mathcal B = \text{CYC}(\mathcal A)$。$\text{Cycle}$ 构造翻译为生成函数即为

\[B(z) = \sum_{k\ge 0} \frac{1}{k}A(z)^k = \log \frac{1}{1 - A(z)} \]

这里仍然需要 $\mathcal A_0 \neq \varnothing$。

$4.4$ 有标号 $\text{Pointing}$ 构造

$\text{Pointing}$ 构造生成了所有可能的“有根”结构。

对于一个有标号类 $\mathcal A$，$\text{Pointing}$ 构造生成了一个有标号类 $\mathcal B$，使得对于任意 $\mathcal A_n$，我们都用 $n$ 个彼此不同的中性对象分别单独标明 $\forall \alpha \in \mathcal A_n$ 中一个单位大小的元素，即对于 $\alpha$ 对应的 $\{\beta\} \subseteq \mathcal B$，有 $\{\beta\} = \{\alpha \}\times \{\epsilon_1, \epsilon_2, \dots, \epsilon_n\}$。容易发现 $\forall \alpha \in \mathcal A_n$ 都生成了 $n$ 个不同的 $\beta \in \mathcal B$；当 $\mathcal A$ 是有标号无根树类时，$\mathcal B$ 就是有标号有根树类。
$\text{PNT}(\mathcal A)$ 又记作 $\Theta \mathcal A$。

容易翻译为生成函数：若 $\mathcal A = \text{PNT}(\mathcal B)$ 则

\[A(z) = \sum_{k\ge 0}k B[k]\frac{z^k}{k!} = z \sum_{k\ge 0}B[k + 1]\frac{z^k}{k!} = z B'(z) \]

这就是 $A = \vartheta B$。

$4.5$ 有标号 $\text{Substitution}$ 构造

$\text{Substitution}$ 构造生成了所有可能的替换生成结构。

$\text{Substitution}$ 构造是二元运算，对有序二元组 $(\mathcal A, \mathcal B)$ 的 $\text{Substitution}$ 构造常记作 $\mathcal A \circ \mathcal B$。$\text{Substitution}$ 构造将前一个有标号类中的元素的每个单位元替换为后一个组合类中的元素。形式化地，定义 $\mathcal S \boxtimes \mathcal T = \{(s, t) \mid s \in \mathcal S, t \in \mathcal T , |(s, t)| = |t|\}$，则有

\[\mathcal A \circ \mathcal B = \sum_{k\ge 0} \mathcal A_k \boxtimes \text{SET}_k(\mathcal B) \]

这翻译成生成函数就是复合：

\[A\circ B(x) = A(B(x)) \]

我们也可以通过这构造来导出其他一些构造。
举例来说，设排列的有标号类是 $\mathcal P$，任意有标号类 $\mathcal A$ 的 $\text{Sequence}$ 构造就是 $\mathcal P\circ \mathcal A$。由于 $P(x) = \dfrac{1}{1 - x}$，我们可以得到 $\text{Sequence}$ 构造的经典表述 $\dfrac{1}{1 - A(x)}$。

在多项式复合的复杂度被优化至 $O(n\log^2 n)$ 后，该构造的适用性逐渐提升。

$4.6$ 有标号和无标号相比

任意有标号类 $\mathcal A$ 都有一个对应的无标号类 $\widehat{\mathcal A}$；$\widehat{\mathcal A}$ 中的元素是由 $\mathcal A$ 中的元素忽略标号得到的。这个过程需要一个等价关系 $\textbf S$，对 $a,b\in \mathcal A$，$a\textbf S b$ 当且仅当存在任意的重标号方案，使得 $a$ 在重标号后可以得到 $b$。那么 $\widehat{\mathcal A} = \mathcal A / \textbf G$。对一个 $\textbf G$ 下元素大小为 $n$ 的等价类，我们（先验地）知道其大小在 $1$ 到 $n!$ 之间，故 $1 \le \dfrac{\lvert \mathcal A_n \rvert}{\lvert \widehat{ \mathcal A } _n \rvert} \le n!$。

至于为什么一个 $n$ 个点的无标号图不一定对应 $n!$ 个有标号图，可以考察经典的反例：一个环根据循环同构只能对应 $(n - 1)!$ 个有标号环。

$\textbf{例 1}$：有/无标号图

令 $\mathcal G$ 表示有标号图的组合类，$\widehat{\mathcal G}$ 表示无标号图的组合类。有标号的情况是好计算的：一个 $n$ 个点的有标号图的所有 $\dbinom n 2$ 条边都是彼此不同的，并且可以任意决定是否选择，那么 $\lvert \mathcal G_n \rvert = 2^{\binom n2} = 2^{n(n-1)/2}$。F. Harary 与 E. M. Palmer 在 Graphical Enumeration 中证明了如下 Pólya 发现的事实：

\[\lvert \widehat{\mathcal G}_n \rvert \sim \dfrac{2^{n(n-1)/2}}{n!} = \dfrac{\lvert \mathcal G_n \rvert}{n!} \]

也就是说，“几乎所有”大小为 $n$ 的图都应当能接受近乎 $n!$ 种不同的标号方法。从组合学的角度，这表明在一个随机无标号图中，我们有很大概率可以通过图的邻接结构分辨出每个点。在这样一种情形下，图没有非平凡的自同构，不同的标号方法数恰好是 $n!$。

与有边的图的情况相对应的是“瓮”（urn）结构，即没有边的图，使用 $\mathcal U$ 和 $\widehat{\mathcal U}$ 表示其组合类。这个组合结构达到了另一个极限情况，即 $\lvert \mathcal U \rvert = \lvert \widehat{\mathcal U} \rvert = 1$。

它们都说明，在 $1 \le \dfrac{\lvert \mathcal A_n \rvert}{\lvert \widehat{ \mathcal A } _n \rvert} \le n!$ 这一普遍的上下界外，没有自然的方法无限制地进行有标号和无标号之间的变换。但若 $\mathcal A$ 是可被构造的，其对应的无标号类可以通过将所有过程中的有标号构造翻译为无标号构造（例如 $\text{SET}\to \text{MSET}$）得到；两个组合类的生成函数都可以被计算出来，进而可以比较系数。

$5.$ 经典的有标号结构应用

接下来要介绍一系列二阶非递归结构，名字源于这些组合类都是通过两次构造得到的。全是例子。

$5.1$ 满射与集合拆分

令组合类 $\mathcal R = \text{SEQ}(\text{SET}_{\ge 1}(\mathcal Z))$ 表示集合的排列，其构造出了离散数学里的基础对象“满射(surjections)”。

在基础数学中，一个从 $A$ 到 $B$ 的满射是映射 $f : A \to B$，且 $B$ 中的每个元素在集合 $A$ 中都有至少一个原像。固定整数 $r \ge 1$，令 $\mathcal R_n^{(r)}$ 是所有集合 $\{1, \dots, n\}$ 到 $\{1, \dots, r\}$ 的满射组成的组合类，其中的元素也可以确切为 $r$-满射。

令 $\mathcal R^{(r)} = \bigcup_n \mathcal R_n^{(r)}$，其生成函数为 $R^{(r)}(z)$。注意到一个 $r$-满射 $\phi$ 可以被一个列举了原像集合的有序 $r$ 元组 $\left(\phi^{-1}(1), \phi^{-1}(2), \dots, \phi^{-1}(r)\right)$ 唯一确定，元组中的各个元素为覆盖了 $\{1, \dots, n \}$ 的不交整数集合。例如，下方为一个 $\mathcal R_9^{(5)}$ 中的元素的可视化表示，最上方为函数图，中间为数据表，最下面为原像序列。（图源 Analytic Combinatorics Figure II.4）

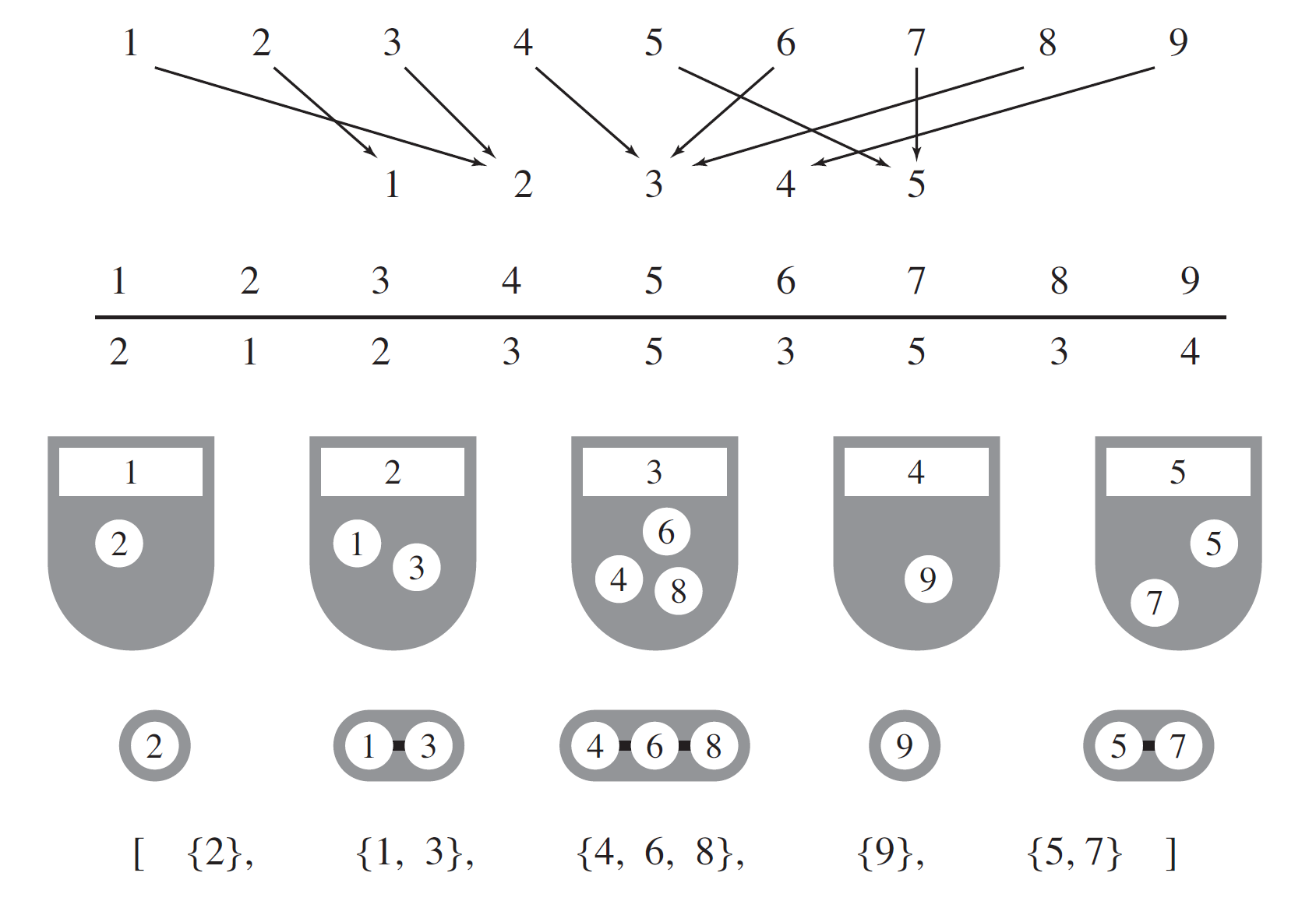
自然可以得到 $\mathcal R^{(r)} = \text{SEQ}_r(\text{SET}_{\ge 1}(\mathcal Z))$，翻译为生成函数即 $R^{(r)}(z) = \left(e^z - 1\right)^r$。其内涵为“满射是非空集合的序列”。

提取系数可以得到

\[R^{(r)}[n] = \left[\dfrac{z^n}{n!}\right] \sum_{i = 0}^r \binom ri (-1)^j e^{(r - j)z} = \sum_{i = 0}^r \binom ri (-1)^j (r - j)^n = r! {n \brace r} \]

我们也要检验一下按照符号化方法推导的 $R^{(r)}(z)$ 是否正确。若不使用符号化方法，那么根据 $\mathcal R_n^{(r)}$ 的组合性质，则有

\[\lvert \mathcal R_n^{(r)} \rvert = \sum_{(n_1, \dots n_r)} \binom{n}{n_1, \dots, n_r} \]

其中求和号枚举所有 $\forall n_k \ge 1, n_1 + \cdots + n_r = n$ 的 $(n_1, \cdots ,n_r)$。那么令 $a_n = [n \ge 1]$，其 EGF 即 $e^z - 1$，而由上，有

\[\begin{aligned} [z^n / n!] R^{(r)}(z) & = \sum_{n_1 + \cdots + n_r = n} \binom{n}{n_1, \dots, n_r} a_{n_1} \cdots a_{n_r} \\ &= \sum_{n_1 + \cdots + n_r = n} \binom{n}{n_1, \dots, n_r} [z^{n_1}/n_1!] (e^z - 1) \cdots [z^{n_r}/n_r!] (e^z - 1) \\ & = [z^n/n!] (e^z - 1)^r \end{aligned} \]

因此 $R^{(r)}(z) = (e^z - 1)^r$，这与我们使用符号化方法推导的结果相同。
最终，$\mathcal R = \bigcup_r \mathcal R^{(r)}$，翻译得到 $R(z) = \sum_{r} R^{(r)}(z) = \dfrac{1}{2 - e^z}$。其系数 $R[n]$ 被称为 Fubini 数（A670）。

类似地，令 $S^{(r)}[n]$ 计数将集合 $\{1, \dots, n\}$ 拆分为 $r$ 个不交且非空的的等价类（被称为块）的方案，其导出的组合类 $\mathcal S^{(r)}$ 中的对象被称为集合拆分。对这个组合类的分析方法和上面的方法相似。

显然地，每个集合分割都能被一个有标号类的集合确定，那么 $\mathcal S^{(r)} = \text{SET}_r(\text{SET}_{\ge 1}(\mathcal Z))$，翻译得到 $S^{(r)}(z) = (e^z - 1)^r / r!, S(z) = \exp(e^z - 1)$。根据上面的推导和常识知道，$S^{(r)}[n]$ 即 Stirling 数，$S[n]$ 即 Bell 数（A110）。

对 Fubini 数和 Bell 数的进一步解析

Fubini 数和 Bell 数的单项可以被展开为简单的无穷求和，如下：

\[R[n] = \left[\dfrac{z^n}{n!}\right] \dfrac{1}{2(1 - \frac{1}{2}e^z)} = \left[\dfrac{z^n}{n!}\right] \sum_{k \ge 0} \dfrac{e^{kz}}{2^{k+1}} = \dfrac{1}{2}\sum_{k\ge 0} \dfrac{k^n}{2^{k}} \]

\[S[n] = \left[\dfrac{z^n}{n!}\right] \dfrac{\exp{e^z}}{e} = \left[\dfrac{z^n}{n!}\right] \dfrac{1}{e} \sum_{k \ge 0} \dfrac{e^{kz}}{k!} = \dfrac{1}{e}\sum_{k\ge 0} \dfrac{k^n}{k!} \]

在 Analytic Combinatorics 例 IV.7 中使用复渐进分析方法对 $R[n]$ 的渐进行为进行了分析；在例 VIII.6 中使用鞍点法对 $S[n]$ 进行了分析，得到的结果如下：

\[R[n] \sim \dfrac{n!}{2(\log 2)^{n+1}} \qquad S[n] \sim \dfrac{n! e^{e^r - 1}}{r^n \sqrt{2\pi r(r + 1)e^r}} \]

其中 $r = r(n)$ 是 $re^r = n + 1$ 的正根。知道 $r(n) \sim \log n - \log \log n$，故 $\log S[n] \sim n(\log n - \log \log n - 1 + o(1))$。对这些渐进形式的初等推导（如只根据实分析）也是可以的，在附录 B.6 Laplace 方法中有简短讨论。

我们仍然能将该方法进一步拓展，得到如下结果。

令 $\mathcal R^{A, B}$ 为原像的基数在 $A \subseteq \mathbb N_+$ 中取，值域大小 $\in B$ 的满射组成的组合类，那么

\[R^{A,B}(z) = \beta(\alpha(z)) \qquad \text{where} \ \alpha(z) = \sum_{a\in A}\dfrac{z^a}{a!}, \beta(z) = \sum_{b \in B} z^b \]

令 $\mathcal S^{A, B}$ 为块的大小在 $A \subseteq \mathbb N_+$ 中取，块的数量 $\in B$ 的集合拆分组成的组合类，那么

\[S^{A,B}(z) = \beta(\alpha(z)) \qquad \text{where} \ \alpha(z) = \sum_{a\in A}\dfrac{z^a}{a!}, \beta(z) = \sum_{b \in B} \dfrac{z^b}{b!} \]

证明：显然 $\mathcal R^{A, B} = \text{SEQ}_{\in B}(\text{SET}_{\in A}(z)), \mathcal S^{A, B} = \text{SET}_{\in B}(\text{SET}_{\in A}(z))$。$\square$

令 $\mathcal S^{(\le b)}$ 和 $\mathcal S^{(\ge b)}$ 为所有块的大小都 $\le b / \ge b$ 的集合拆分组成的组合类，那么令 $\exp_b z = \exp z \bmod z^{b + 1}$ 为截断指数函数，这两个组合类的生成函数显然分别为 $\exp(\exp_b z - 1)$ 和 $\exp(\exp z - \exp_b z)$。简单差分即可得到限制最大/最小元素恰好为 $b$ 的组合类的生成函数。

如何在限定块大小/块数量的奇偶性的条件下计数集合拆分？使用上面的结论，以及 $\exp z, \sinh z, \cosh z$ 分别为 $\mathbb N_+, 2\mathbb N_+, 2\mathbb N_+ + 1$ 的生成函数，知道

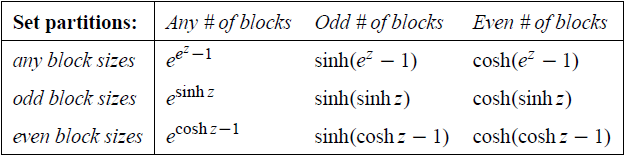
这表被称为 Comtet's square。

一个大小为 $n$ 的排列（arrangement）是集合 $\{1, \dots, n\}$ 中的（部分）元素的有序组合。若其由 $r$ 个元素组成，那么其被确切为 $r$-排列。令 $\mathcal A$ 为排列组成的组合类，那么自然有 $\mathcal A = \text{SET}(\mathcal Z) \times \text{SEQ}(\mathcal Z)$，翻译为生成函数即 $A(z) = \dfrac{e^z}{1 - z}$。

$5.2$ 指数型概率生成函数

在本小节中，我们将通过“生日悖论”和“赠券收集问题”向读者展示符号化方法是如何在分析离散概率模型时发挥作用的。

考虑这样一个模型：有很长很长一队人，要一个一个地进入一个很大很大的屋子。每个人在进入的时候都会宣布他的生日。那么，至少需要进入多少人，屋子里才能有两个人生日相同？生日悖论宣称，发生生日碰撞时人数的期望约为 $24$，尽管这是反直觉的。对偶地，赠券收集问题关注屋子里的人的生日取遍每个可能的日期时房间里的人数（所谓“赠券收集”，是指物品在售卖时会附赠一些图卡或赠券，收集一整套便可得到一些奖励）。赠券收集问题说明，全收集时的期望约为 $2364$，相当大。

这两个问题都有关于可能无穷长的事件列，然而若固定时间 $n$，第一次生日碰撞或完全收集就只关于有限个事件。考察确定的一个无穷长的事件列，满足生日碰撞和全收集这两个事件全部出现，那么在 $n$ 趋向于无穷的过程中，总有两个时刻 $B, C$，使得在 $B$ 时发生生日碰撞，$C$ 时全收集。而在时间 $n \in [0, B)$ 时，进入房间的人和生日间形成了单射关系；在时间 $n \in [C, +\infty)$ 时，进入房间的人和生日间形成了满射关系。换句话说，我们要找的就是单射性终止的时刻 $B$，和满射性起始的时刻 $C$。接下来，我们考虑一年有 $r$ 天（来自地球的读者也许会取 $r = 365$），并将一个生日列看作一个单词，相关的字母表 $\mathcal X$ 中有 $r$ 种字母，每种表示一天。

令 $B$ 为第一次发生碰撞的时间，据鸽笼原理，显然 $B$ 是一个在 $2$ 到 $r + 1$ 间的整数中取值的随机变量。若生日列 $\beta_1, \dots, \beta_n$ 没有重复，那么在时间为 $n$ 时还未发生碰撞。换句话说，函数 $\beta : \{1, \dots, n\} \to \mathcal X$ 必为单射；等价的，$\beta_1, \dots, \beta_n$ 是大小为 $r$ 的 $n$-排列。故，我们得到了如下的关系：

\[\mathbb P[B > n] = \dfrac{r}{r} \cdot \dfrac{r - 1}{r} \cdots \dfrac{r - n + 1}{r} = \dfrac{r^{\underline{n}}}{r^n} = \dfrac{n!}{r^n} [z^n](1 + z)^r = \left[\dfrac{z^n}{n!}\right]\left(1 + \dfrac{z}{r}\right)^r \]

又，显然地有

\[\mathbb E[B] = \sum_{n\ge 0} \mathbb P[B > n] \]

当 $r = 365$ 时，我们有 $\mathbb E[B] \approx 24.616585894598853923$。

你想知道它具体是哪个分数吗？

借助 mathematica，我们可以得到

\[\mathbb E[B] = \frac{12681734596528349115032945867187812535439682980771152407666931547220091311548596996746373722294695723515706582674935613381706118425147562280440279219869392678414008272499519769381637499846752041259302700246874852192652090630098961981787684412821259661575009238409727070488184114629887275361462969176225544391041429106914593618359436215252782863332035169258963565834305376626343757905461048111867743585428064887338404657617703006119953217785027948223080584915722409440560026311463820692962637055114594928715849753117620039252666970293149627484038926001281193986783966997653047135739446387350350760744207597933678686815678257690979124805442057850794129734892908325602981727849380511166071832149397323944478527653360459965005498781180475765137989850406461228049511925136040348842215061015569402112227139617230042567471204888574801140295843319199802641658972286465106674}{515170326658127653023270268934968831864006656970059803702471762685413738371922676540955719255176033837628306315825181877150741759238731487936775212190033564135520192401974269458851863217125548343091322801534117245573443413531922275612913528038368117246368938917573264013996463001304954829864348817232466436717311856873167200871359539951780183986982019981454546048785471012647019662520753069879400574056837803950541557117787442934714835950267467275488609709127945889546366868819498143130928828104709275844760637935840192366628163101930811267397402954354789999800088756824182179122318041220995650232069431164178955161360483122690952293589731983424333163050451909518452256437800568549944499327426042068267202215812972708997217666469620959661388470725356466960622014888773469229307515572285821265768570192890040020733139958437375727218210386126884259283542633056640625} \]

《解析组合》里只取分子分母的前后几位不是没有道理的。听说分母有 864 位，我看了看还真是。

这个期望的另一种表示方式是从 $\mathbb P[B > n]$ 的生成函数形式导出的。使用 Laplace 变换的一个特例，我们可以计算

\[\mathbb E[B] = \sum_{n \ge 0} \left[\dfrac{z^n}{n!}\right]\left(1 + \dfrac{z}{r}\right)^r = \int_0^{\infty} e^{-t} \left(1 + \dfrac{t}{r}\right)^r \mathrm dt \]

这时就可以进行渐进分析了。离散形式和积分形式都可以施用 Laplace 方法，二者均可以得到如下的估计：

\[\mathbb E[B] = \sqrt{\dfrac{\pi r}{2}} + \dfrac 23 + O(r^{-1/2}) \qquad (r \to + \infty) \]

Knuth 在 The Art of Computer Programming, 3rd ed., vol. 1: Fundamental Algorithms 中用该计算作为一个（实）渐进分析的例子。值得注意的是，当 $r = 365$ 时，前两项给出的估计是 $24.61\mathit{119}$，和实际的 $24.61\mathit{659}$ 仅有约 $2\cdot 10^{-4}$ 的相对误差。

这种基于生成函数的积分表示的优点在于稳健性（robust）：它们能自然地适应多种组合条件。举例来说，相同的计算方法可以证明，第一次出现“$b$ 个人有相同的生日”这一事件的期望时间由下面的积分给出：

\[I(r, b) = \int_0^\infty e^{-t} \exp_{b - 1}(t / r)^r \mathrm dt \]

M. S. Klamkin 和 D. J. Newman 于 1967 年在它们的论文 Extensions of the birthday surprise 中提出了这一公式，并使用 Laplace 方法指出

\[I(r, b) \sim r^{1 - 1/b} \Gamma\left(1 + \dfrac{1}{b}\right)\sqrt[b]{b!} \qquad (r \to +\infty) \]

当 $r = 365, b = 3$ 时这一近似给出 $82.87$，而实际值为 $88.73891$。由此也可以知道，三次碰撞比我们想的要更久，期望在进入几乎 89 个人后才会发生。这一应用也能说明符号化方法的多功能性，以及其在经典概率问题上的应用能力。

赠券收集问题是生日悖论的对偶问题。我们要求的是一个 $C$，满足 $\beta_1, \dots, \beta_C$ 包含了 $\mathcal X$ 中的所有元素，也就是所有可能的生日都被“收集”了。换句话说，事件 $C \le n$ 说明了 $\{\beta_1,\dots,\beta_n\} = \mathcal X$。那么有

\[\mathbb P[C \le n] = \dfrac{R_n^{(r)}}{r^n} = \dfrac{n!}{r^n} [z^n] (e^z - 1)^r = \left[\dfrac{z^n}{n!}\right] (e^{z/r} - 1)^r \]

\[\mathbb P[C > n] = 1 - \mathbb P[C \le n] = \left[\dfrac{z^n}{n!}\right] \left(e^z- (e^{z/r} - 1)^r \right) \]

那么

\[\mathbb E[C] = \int_0^\infty e^{-t} \left(e^t- (e^{t/r} - 1)^r \right) \mathrm dt = \int_0^\infty \left(1 - (1 - e^{t/r})^r \right) \mathrm dt \]

对其进行二项式展开并逐项积分得到一个并不好看的结果

\[\mathbb E[C] = r \sum_{i = 1}^r \binom{r}{i} \dfrac{(-1)^{i - 1}}{i} \]

或者作换元 $v = 1 - e^{-t/r}$ 并展开、逐项积分得到 $\mathbb E[C] = r H_r$（$H_n$ 是调和数）。顺便一提，这个式子其实是很好“感性”得到的：我们平均需要进入 $r / r$ 人才能得到第一天，需要 $r / (r - 1)$ 人才能得到不同的一天，以此类推。但这样的初等推导方法十分依赖问题的结构：不像符号化方法，这样的方法一般无法推广到更复杂的情况。

接下来的事情就较为简单了，熟知 $r \to +\infty$ 时 $H_r = \log r + \gamma + 1/2r + O(r^{-2})$，其中 $\gamma \approx 0.5772156649$ 是 Euler 常数，那么

\[\mathbb E[C] = r\log r + \gamma r + \dfrac{1}{2} + O(r^{-1}) \qquad (r \to +\infty) \]

一个反常识的事情是，它并不是随着 $r$ 线性增长的。对地球上的一年来说，$r = 365$，精确的期望约为 $2364.646\mathit{02}$，而上方给出的由前三项导出的值为 $2364.646\mathit{25}$，相对误差仅为千万分之一。

类似的，符号化方法也能处理推广后的情况，例如多次全收集。我们知道，每个物品都被收集了至少 $b$ 次的期望时间为

\[J(r, b) = \int_0^{\infty} \left(1 - \left(1 - \exp_{b - 1} (t - r)e^{-t/r}\right)^r\right)\mathrm dt \]

从这个式子中，我们得到

\[J(r, b) = r \left(\log r + (b - 1) \log \log r + \gamma - \log(b - 1)! + o(1) \right) \qquad (r \to +\infty) \]

因此只需要再多收集很少的次数，我们就能达成多次全收集。

如果收集赠券的人有一个小妹，他会把多余的赠券都给她，那么 Foata, Lass 和 Han 证明了当大哥首次全收集时，小妹错过的赠券的期望种类数是 $H_r$。

$5.3$ 一排环、一堆环

本节要介绍两个构造结构：环的序列，以及环的集合。它们分别构造了对中(alignment)类，以及提供了一个新颖的观察排列的角度，即排列的环分解。形式化地，令组合类 $\mathcal O = \text{SEQ}(\text{CYC}(\mathcal Z))$ 为由对中组成的有标号类，$\mathcal P = \text{SET}(\text{CYC}(\mathcal Z))$ 为排列的组合类。

对中是由有标号环组成的序列，其是强标号的。我们可以把对中想象为线性排成一列的有向循环集合，有些像垂直穿在签子上的一排香肠片。根据符号化方法，我们可以写出他的生成函数为

\[\mathcal O = \text{SEQ}(\text{CYC}(\mathcal Z)) \quad \Longrightarrow \quad O(z) = \dfrac{1}{1 - \log(1 - z)^{-1}} \]

其系数为 A7840，组合意义是排列的有序环分解。这个系数数列看上去没有简单的形式。

存在一种方法，将排列唯一地分解为有标号有向环。我们取一个长为 $n$ 的排列 $\sigma$，它是 $\{1,\dots,n\}$ 上的置换。再取一张 $n$ 个点、无边的图。从某个元素开始，例如 $1$，并连 $1 \to \sigma(1)$ 的有向边，连 $\sigma(1) \to \sigma^2(1)$ 的有向边，以此类推，至多 $n$ 步后得到一个包含 $1$ 的环。若我们依次在所有孤立点上重复这一构造，就能得到一张表示 $\sigma$ 的环分解的，由有向环组成的图。因此，有标号有向环组成的有标号类和排列的有标号类是组合同构的，故

\[\mathcal P = \text{SEQ}(\mathcal Z) \cong\text{SET}(\text{CYC}(\mathcal Z)) \quad \Longrightarrow \quad P(z) = \exp \log \dfrac{1}{1 - z} = \dfrac{1}{1 - z} \]

从中看出，$\exp$ 和 $\log$ 互为逆运算不过是“排列可以唯一地分解为环”这一组合事实的解析反映。

令 $\mathcal P^{A, B}$ 为环长度在 $A \subseteq \mathbb N_+$ 中取，环数 $\in B$ 的排列组成的组合类，那么

\[P^{A,B}(z) = \beta(\alpha(z)) \qquad \text{where} \ \alpha(z) = \sum_{a\in A}\dfrac{z^a}{a}, \beta(z) = \sum_{b \in B} \frac{z^b}{b!} \]

令 $\mathcal O^{A, B}$ 为环长度在 $A \subseteq \mathbb N_+$ 中取，环数 $\in B$ 的对中组成的组合类，那么

\[O^{A,B}(z) = \beta(\alpha(z)) \qquad \text{where} \ \alpha(z) = \sum_{a\in A}\dfrac{z^a}{a}, \beta(z) = \sum_{b \in B} z^b \]

我们关注恰好由 $r$ 个环组成的排列，它的组合类记为 $\mathcal P^{(r)} = \text{SET}_r(\text{CYC}(\mathcal Z))$，翻译为生成函数为 $P^{(r)}(z) = \dfrac{1}{r!}\left(\log \dfrac{1}{1 - z}\right)^r$。故自然得到长度为 $n$ 的这类排列的计数 $P^{(r)}[n] = \dfrac{n!}{r!}[z^n]\left(\log \dfrac{1}{1 - z}\right)^r$。它们又称第一类 Stirling 数，或——按 Knuth 的提议——Stirling 环数（cycle number）。Graham，Knuth 与 Patashnik 的书《具体数学》中深入研究了该数列和 Stirling 拆分数（即第二类 Stirling 数）的性质。

同样的，我们也关注在长度为 $n$ 的随机排列中的环分解情况。显然，当随机是在 $\mathcal P_n$ 上均匀随机选择时，每个排列对应的概率都是 $1/n!$。由概率的定义，随机变量 $P_n$ 有 $k$ 个环的概率为

\[p_{n, k} = \dfrac{1}{n!}{n\brack k} \]

可以直接 $O(n^2)$ 递推得到 $n$ 确定时所有 $p_{n, k}$ 的值。计算可得，当 $n = 100$ 时，绝大部分排列的环数都在 $[1,10]$ 内（补事件的概率仅为约 $0.0059$）；均值约为 $5.18$。那么我们可以称：一个长为 $100$ 的随机排列平均有五个多一点的环，并且几乎不可能有大于十个环。

上面的步骤描述了符号化方法的一个直接用法。但它不会告诉我们 $n$ 趋向于正无穷时环数是如何由 $n$ 决定的。在此我们对这个问题的解答仅作简要叙述。首先，构造二元生成函数

\[P(z, u) = \sum_{r\ge 0} P^{(r)}(z) u^r \]

注意到

\[P(z, u) = \sum_{r\ge 0} \dfrac{u^r}{r!} \left(\log \dfrac{1}{1 - z}\right)^r = \exp\left(u \log \dfrac{1}{1-z}\right) = (1 - z)^{-u} \]

由牛顿二项式定理和上指标反转得到 $[z^n](1 - z)^{-u} = (-1)^n \dbinom{-u}{n} = \dbinom{n + u - 1}{n}$，故

\[\sum_{k = 0}^{n} p_{n, k} u^k = \dbinom{n + u - 1}{n} = \dfrac{u(u + 1) (u + 2) \cdots(u + n - 1)}{n!} \]

根据对数微分法得到均值

\[\mu_n = \sum_k k p_{n, k} = 1 + \dfrac 12 + \cdots + \dfrac 1n = H_n \]

故我们得到 $\mu_{100} = H_{100} \approx 5.18738$。总之，一个长为 $n$ 的随机排列的平均环数随 $n$ 对数级增长。

错排的经典定义是指没有稳定点的排列，即 $\forall i, \sigma(i) \neq i$。给定整数 $r$，一个 $r$-错排是一个所有环的长度都大于 $r$ 的排列。令所有 $r$-错排组成组合类 $\mathcal D^{(r)} = \text{SET}(\text{CYC}_{> r} (\mathcal Z))$，那么

\[D^{(r)}(z) = \exp \left(\sum_{j > r} \dfrac{z^j}{j}\right) = \dfrac{1}{1 - z}\exp \left(-\sum_{j = 1}^r \dfrac{z^j}{j}\right) \]

例如，当 $r = 1$ 时，有

\[\dfrac{D^{(1)}[n]}{n!} = 1 - \dfrac{1}{1!} + \dfrac{1}{2!} - \cdots + \dfrac{(-1)^n}{n!} \]

它是 $e^{-1}$ 的级数展开的截断。换个方式陈述，它就变成了一个经典的组合问题，并且有一个令人愉悦的十九世纪古朴阐述：“$n$ 个人进入剧院，在衣帽寄存处的钩子上挂上了它们的帽子，并在离开的时候随机拿了一顶；那么没有人得到自己原来的帽子的概率趋近于 $1/e$，约为 37%”。通常的证明使用了容斥原理。（这也反映出时代的变化，因为 R. Motwani 和 P. Raghavan 在他们 1995 年出版的书 Randomized Algorithms 中将这个问题描述为一个醉酒状态下的水手返回船只，并随机选择一个船舱睡觉。）

对广义错排问题，我们有对任意确定的 $r$，$\dfrac{D^{(r)}[n]}{n!} \sim \exp \left(-H_r\right) \quad (n\to+\infty)$ 都成立。这个公式可以使用复渐进分析方法简单证明。

参考资料：
《Analytic Combinatorics》, Philippe Flajolet and Robert Sedgewick ;
oi-wiki 符号化方法, hly1204 et al. ;
多项式计数杂谈, command_block ;
组合结构符号化学习笔记, x义x ;
抄袭 x义x 的 Symbolic Method 讲义, alpha1022 ;

待补：增加有标号例题

posted @ 2023-01-31 20:43 joke3579 阅读(2077) 评论(3) 收藏举报

刷新页面返回顶部

Dr. Zhou

joke3579

符号化方法

\(1.\) 无标号体系

\(1.1\) 记号与定义

\(1.2\) 基础无标号类

\(1.3\) 例题

\(2.\) 经典的无标号构造

\(2.1\) 集合的 \(\text{Sequence}\) 构造

\(2.2\) 集合的 \(\text{Multiset}\) 构造

\(2.3\) 集合的 \(\text{Powerset}\) 构造

\(2.4\) 集合的 \(\text{Amplification}\) 构造

\(2.5\) 集合的 \(\text{Cycle}\) 构造

\(2.6\) 有限制的构造

\(2.7\) 隐式构造

\(3.\) 有标号体系

\(3.1\) 概述

\(3.2\) 记号与定义

\(3.3\) 基础有标号类与操作

\(4.\) 经典的有标号构造

\(4.1\) 有标号 \(\text{Sequence}\) 构造

\(4.2\) 有标号 \(\text{Set}\) 构造

\(4.3\) 有标号 \(\text{Cycle}\) 构造

\(4.4\) 有标号 \(\text{Pointing}\) 构造

\(4.5\) 有标号 \(\text{Substitution}\) 构造

\(4.6\) 有标号和无标号相比

\(5.\) 经典的有标号结构应用

\(5.1\) 满射与集合拆分

\(5.2\) 指数型概率生成函数

\(5.3\) 一排环、一堆环