论文“A Minimum Distortion Noise Reduction Algorithm With Multiple Microphones”阅读笔记

 

一. 该问题的模型：

s(k)为源信号；gn表示从源到麦克风的声通道脉冲响应；

xn(k)、vn(k)、yn(k)分别为在第n个麦克风上观察到的语音、背景噪声，麦克风的实际收到的混合信号

 

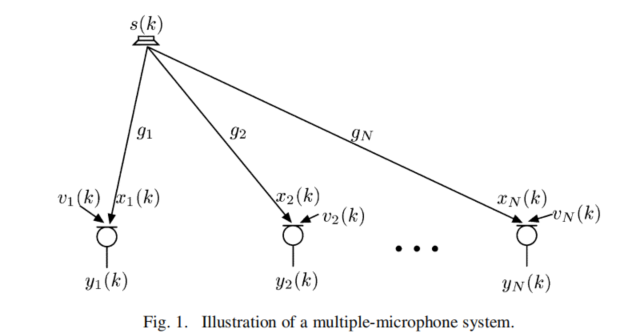
N个麦克风，设定中背景噪声v(k)与x(k)，假设两者和都是相互不相关的零均值随机过程。

二. 模型的数学描述：

 

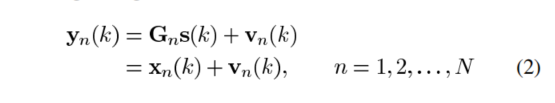
其中：

 

 

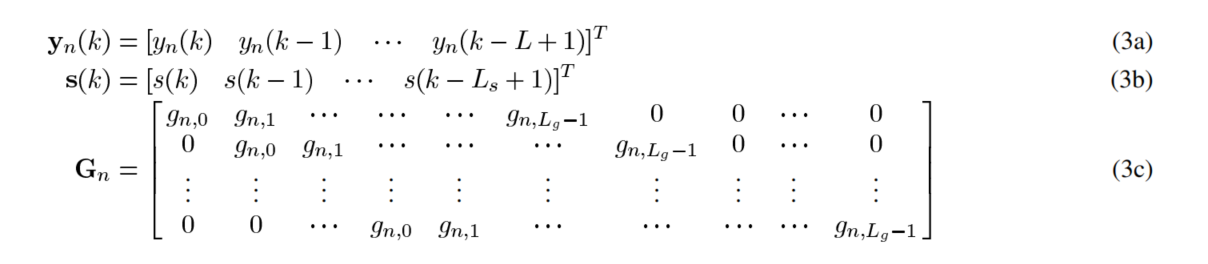
 Gn矩阵大小是信道脉冲响应的长度，L X Ls，Ls=L+Lg-1，Lg是通道脉冲响应的长度

y、x、v都是L X 1的向量。

三、算法描述

 1.第m路的信号可以通过N个麦克风接收到的信号，再通过N个h滤波器进行还原。其中h(1m)，h(2m)代表的是以还原第m个为参考的麦克风，应用于第一个麦克风的滤波器h1，以及应用于第二个麦克风的滤波器h2。

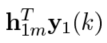是1 X L的向量和L X 1的向量相乘最后得到的一个具体的数字

 

 

Xm(k)最后是通过N个数字相加得到的结果：

 通过该方法得到的信号的误差是：

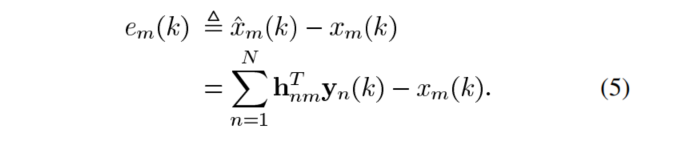
将等式（2）代入(5)中可以得到：

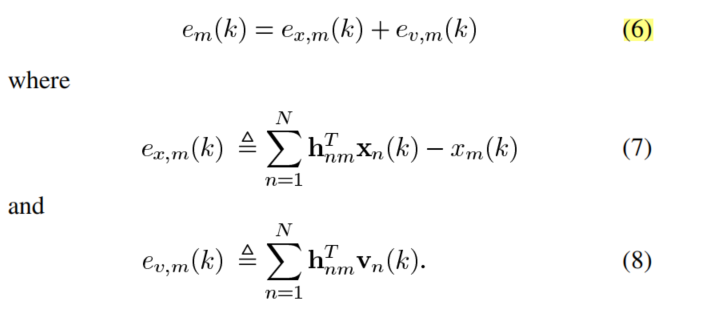
其中ex,m(k)代表失真程度，越大证明越失真；ev,m(k)代表噪声抑制强度，是N个数字相加的结果，越小表示残存噪声越小。

在这种情况下，该方法的目标是：在保持语音失真接近于0时(ex,m(k) = 0)，尽量减小残存噪声的均方误差（MSE)。

2.此时构造的目标函数就是：

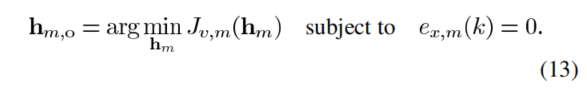
 角标o是指最优化的，最优的。

寻找最优滤波器，约束条件是语音信号不失真.

 

 其中：

 

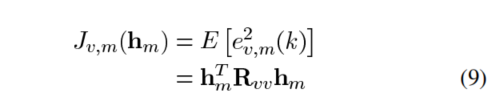
Jv,m(hm)是对ev,m(k)求均方值

 

 

 

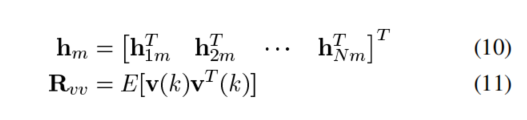
注意此时：

v(k)是一个N X L的矩阵，代表N个麦克风的v的集合

hm是N x L的矩阵，代表N个麦克风滤波器h的集合

 

 

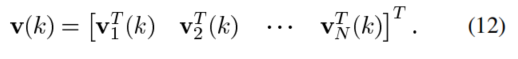
3.引入预测矩阵后的目标函数

假设能找到预测矩阵Wnm(n = 1，2，3,...N)。

 

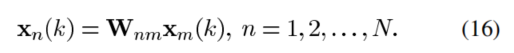
（16）表示通道n可以由通道m预测得到，对于每个n麦克风，都有一个对应的Wnm。

1）当n = m时，Wnm=I，单位阵

2）当n≠m时，将（16）带入方程（7）中得到

 

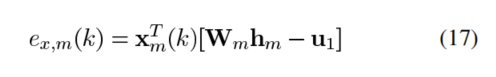
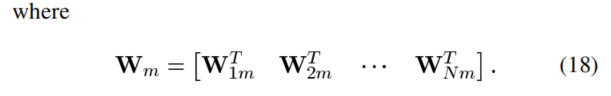
其中hm代表N个麦克风滤波器h的集合。Wm是N个Wnm的集合

所以利用（17），得到新的目标函数：

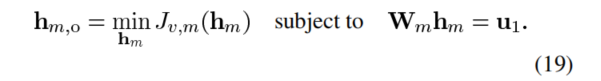
角标o是指最优化的，最优的。

利用拉格朗日乘子法算出的最优滤波器解是：

 

 

 

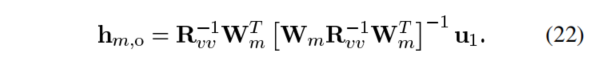
(假设麦克风上的噪声信号不是完全相干的，因此噪声协方差矩阵Rvv是全秩的）

为了得到最优滤波器h，需要知道两个矩阵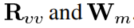

Rvv可以在没有语音的时期进行估计,Wm的计算如下一小节。

 

4.预测矩阵的更新

 

根据（16），构造出MSE cost函数

 

 

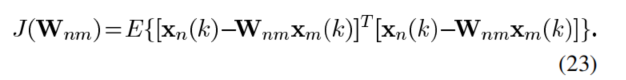
对Wnm的最优估计：

 

 

 

 

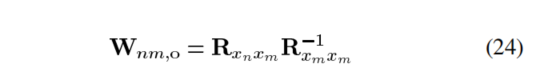
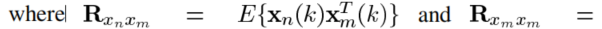
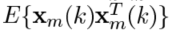
前者是n和m麦克风的互相关系数，后者是第m个麦克风的自相关系数。

 

利用（2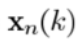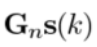）=，可以将两个相关系数改为：

 

 

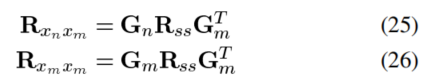
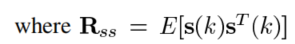 ,是源相关矩阵

 

所以(24)被改写为：

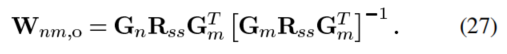
当源信号s(k)为噪声信号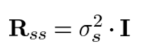时，，此时：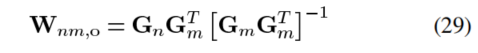

 

但是在现实中，源信号并不是白噪声，所以不W仅依赖于通道脉冲响应，还依赖于源相关矩阵。

 

由于xn(k）和xm(k)都是不可得到的，所以利用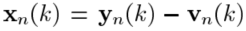和噪声和语音是不相关的，可以简化为：

 

 

 

 

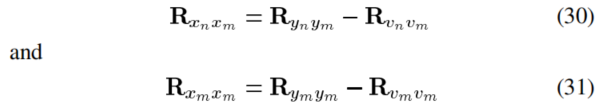
所以（24）可以改为：

 

       

 

(32)中的统计量都可以从观测到的信号中计算出来。

 

如果我们使用语音活动检测器(VAD)，就可以在沉默期间估计噪声特征。

 

将(32)或者(24)带入(22)中，可以得到最后的最优滤波器:

 

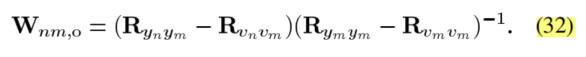
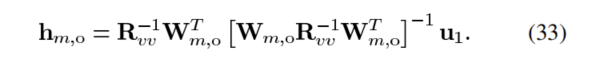
此时理论上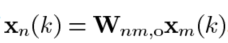，用对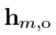观测到的信号进行滤波可以不引入语音失真。

在实际情况中，无法确定是否。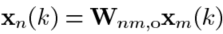

所以这样就可能会有一些语音失真。然而，对于长滤波器，我们可以接近这个等式，这样失真就可以保持在很低的水平。

 

该论文MVDR算法的特点：

1)不需要阵列几何信息；

2)不需要估计DOA（direction of arrival）或房间脉冲响应；

3)它在远场和近场情况下都是一样的；

4)它可以产生非常好的和稳健的降噪，实际上最小的语音失真。

 

附别的情况：

如果源信号和噪声都是白随机过程，且工作环境没有混响，所开发的多通道降噪算法将退化为delay-sum波束形成。

如果环境没有混响，当源信号是语音时，上述多信道算法可以视为filter-and-sum形成器的一种特殊情况。