pytorch_10卷积神经网络(基础篇)
全连接层:即前面提到的全连接神经网络的线性层linear layer,每一个输入结点都要参与到下一层的任何一个输出结点上。
卷积神经网络 Convolution Neural Network
问题引入:之前在MINIST 中,用的是全连接神经网络,即将图像转化为1*28*28的张量,然后将张量转为矩阵形式输入,是一整行的数据。以这种形式可能会造成两个相邻节点在矩阵中隔得远,即做成全连接后丧失了图像的空间特征,由此引入卷积神经网络,把图像按照原始的的空间结构进行保存,从而可以保留原始的空间信息。
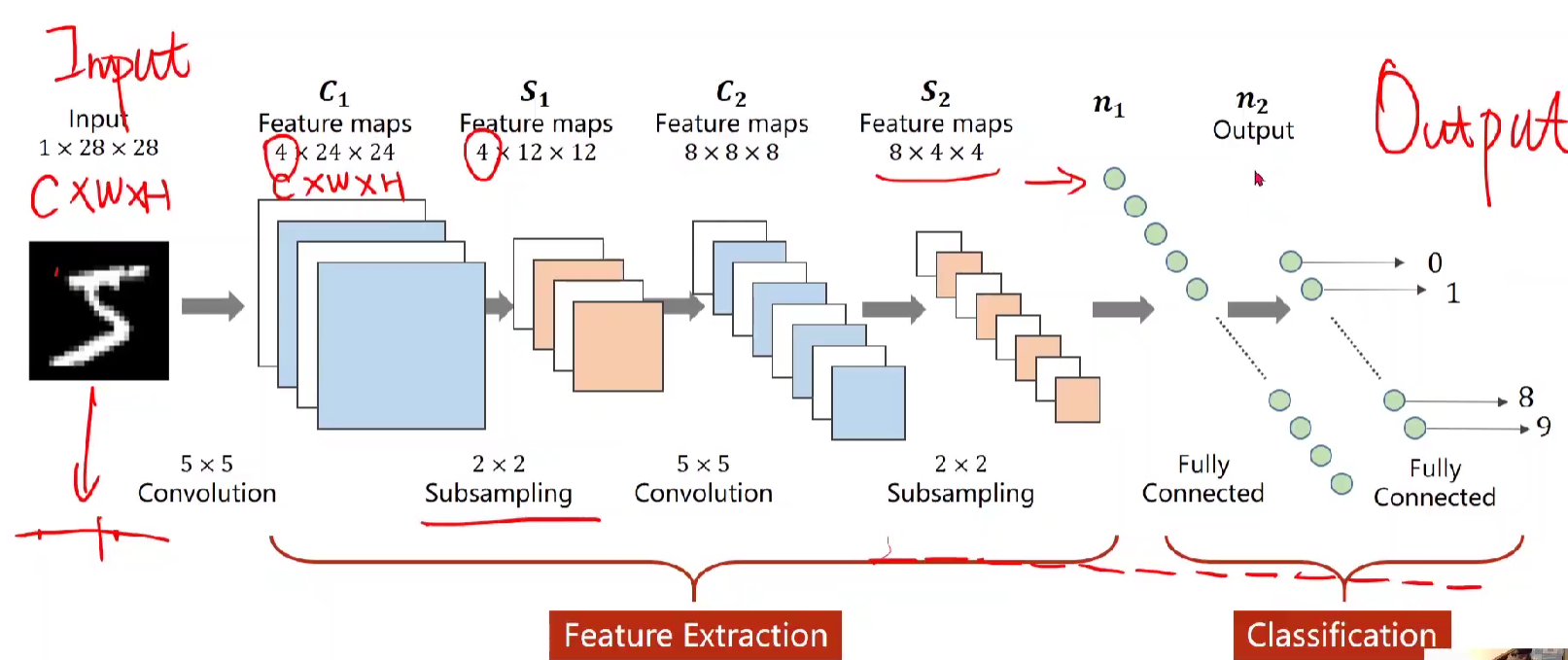
kernel是 5 * 5 (下面红色编号为特征提取Feature Exatraction, 3,4为Classification)
1.把input 进行5*5卷积,其中要注意这里通道数、W 、 H都会发生改变(当然,也可以不变),在这边,一个图像扔到卷积层中依然是一个三维的张量。
2.进行2*2 的下采样,通道数是不变的,但是W、H会发生改变。下采样目的为减少元素数量,降低运算需求。
3.到绿色部分,进行全连接,把张量展开为向量(上一节用到的view),得到n1.
4.再一次全连接 ,映射到十维的输出n2.
5.然后就用softmax计算交叉熵损失。
即不断地进行过卷积、下采样等大小的变化,把1*28*28转化成十维的向量,即放到十维的线性空间。(先明确输出要得到啥,然后不断运用各种层进行维度上或每个维度上尺寸大小的变化,从而最终映射到我们想要的空间。)
Convolution 卷积
一些概念:
- 栅格图像:从自然界获取图像的方式。
* 单色图像采集:通过光敏电阻获取像素,通过每个电阻来获得该光锥的光强。
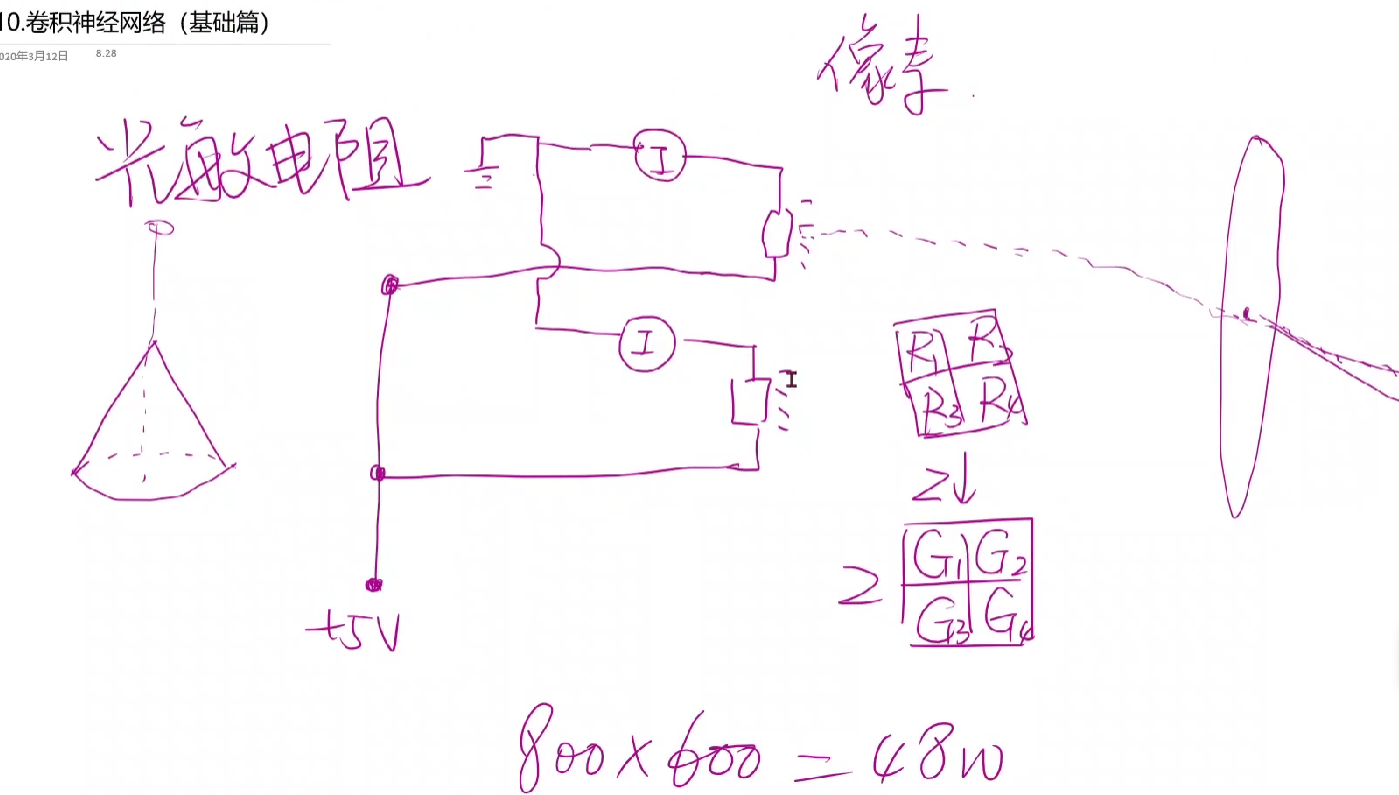
* 彩色:RGB。灰度值0-255,将数据转变为图像。
- 矢量图象:描述圆心,直径、边、填充。这里要区分于栅格图像,栅格图像是很多个像素提前存到一个个格子里,所以放大之后就像一个个马赛克; 而矢量图象是描绘的。
关于卷积要做的:
——>栅格图像,所以把 图像放到R、G、B三个channel【Input Channel】,如下图
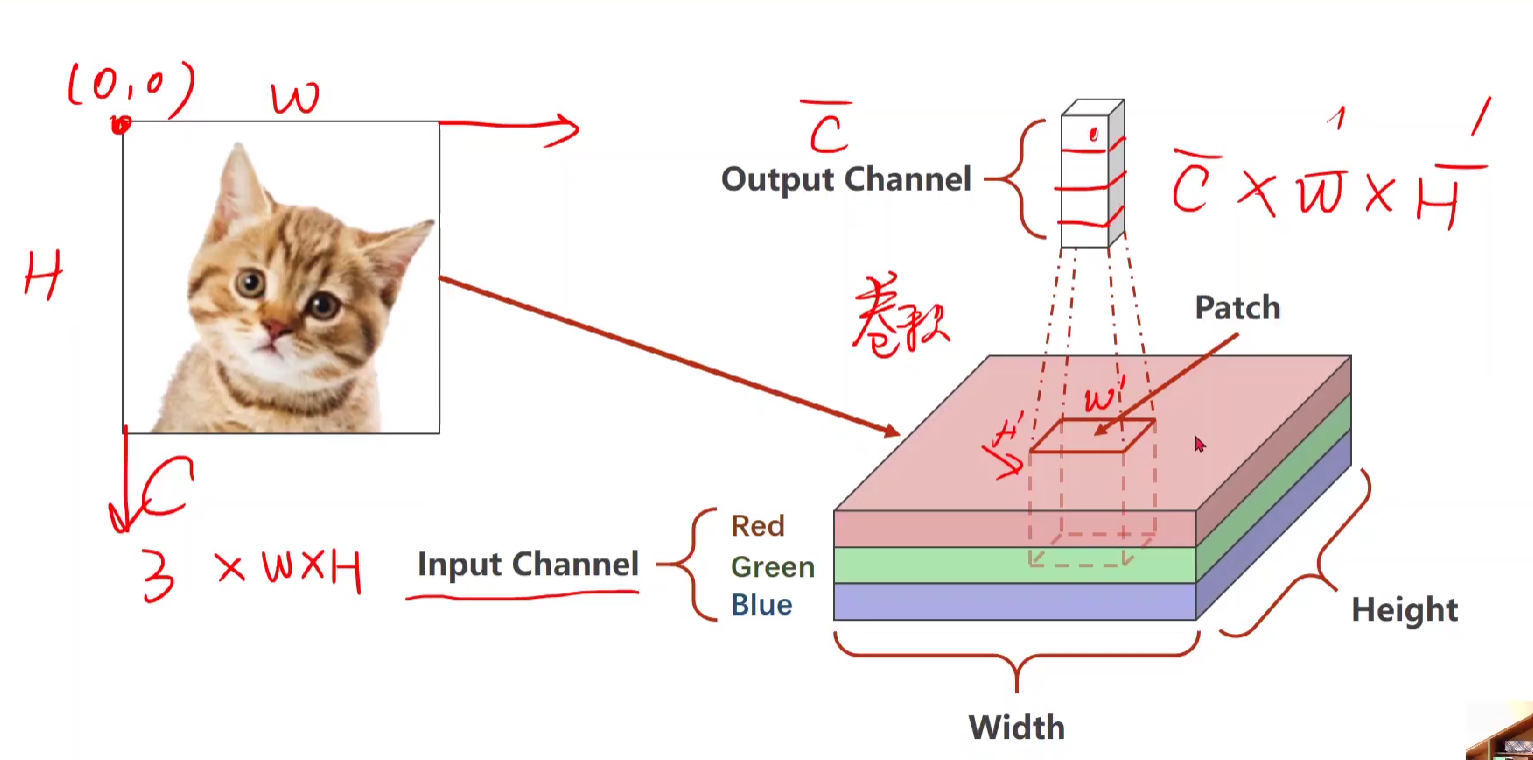
先在input里面取一个块patch [ h‘,w' ],然后开始在图像块中移动,对patch进行卷积操作,得到C、,W、H 都变的块,即上图的output。
通过对patch每个像素进行加权求和,所以output里面包含了全部信息,有点特征提取的意思,对patch进行加权,可以让满足该特征的值变大,不满足的变小。
卷积的运算过程:
♦单通道single:
使用3*3卷积核进行数乘,得出output
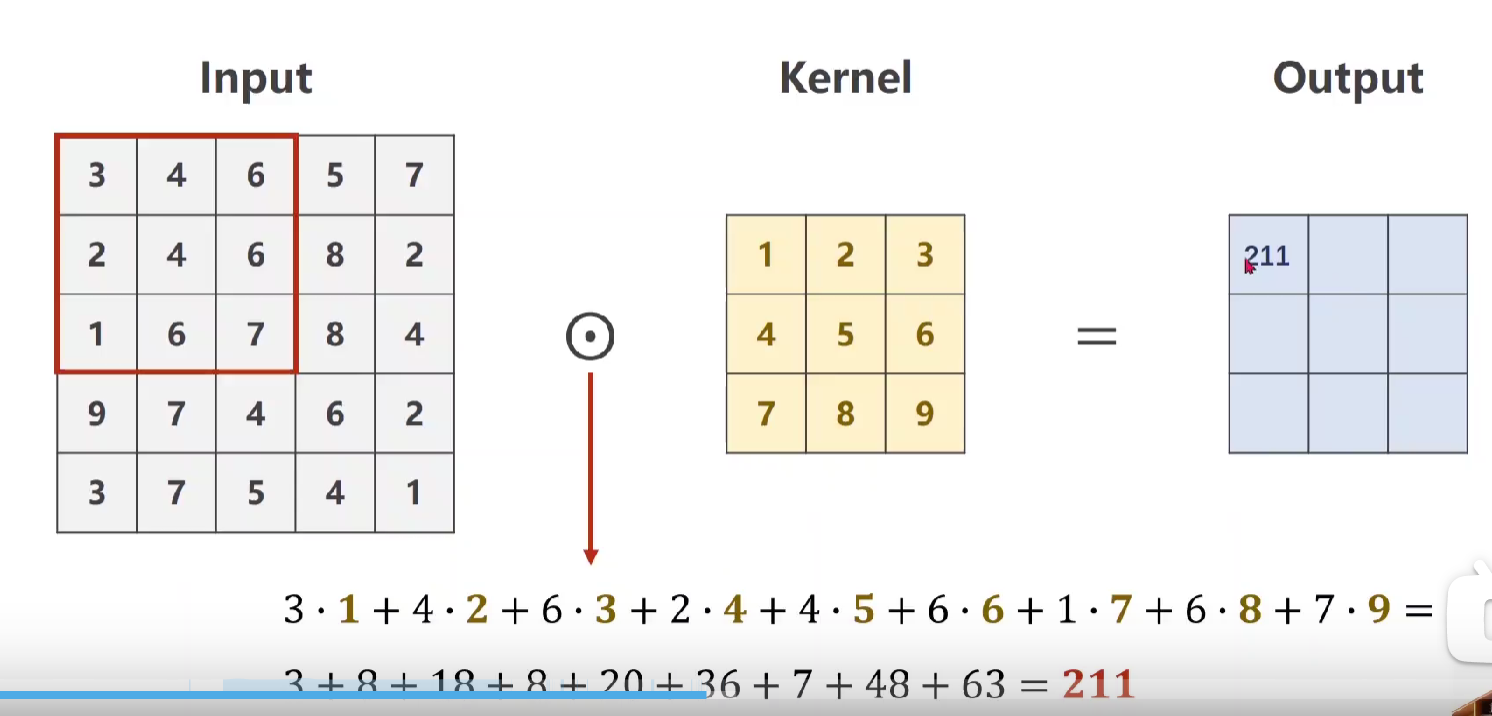
♦三通道(神经网络中可能达到几百个通道,这里以三通道RGB为例)
- 对每一个通道做卷积,数乘后求和,该过程其实就是卷积运算。
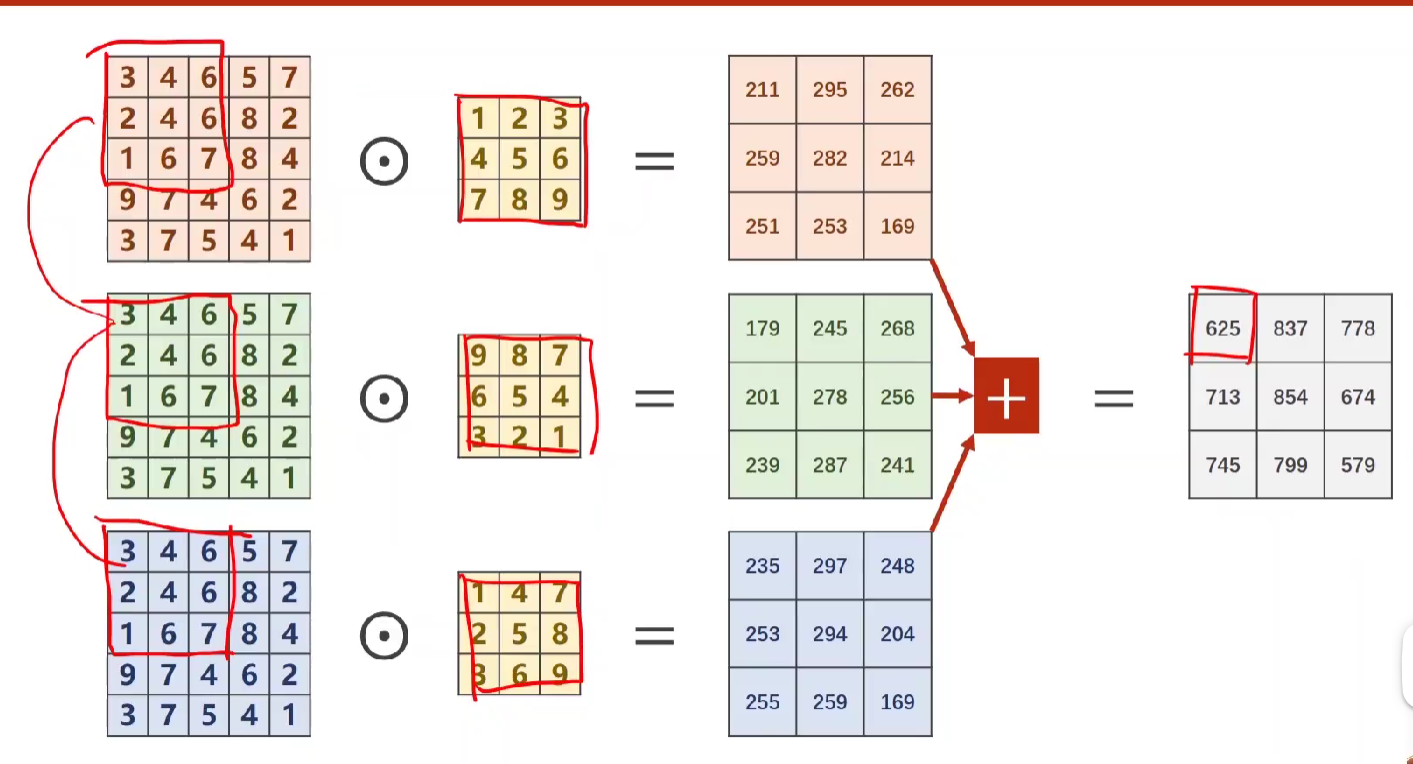
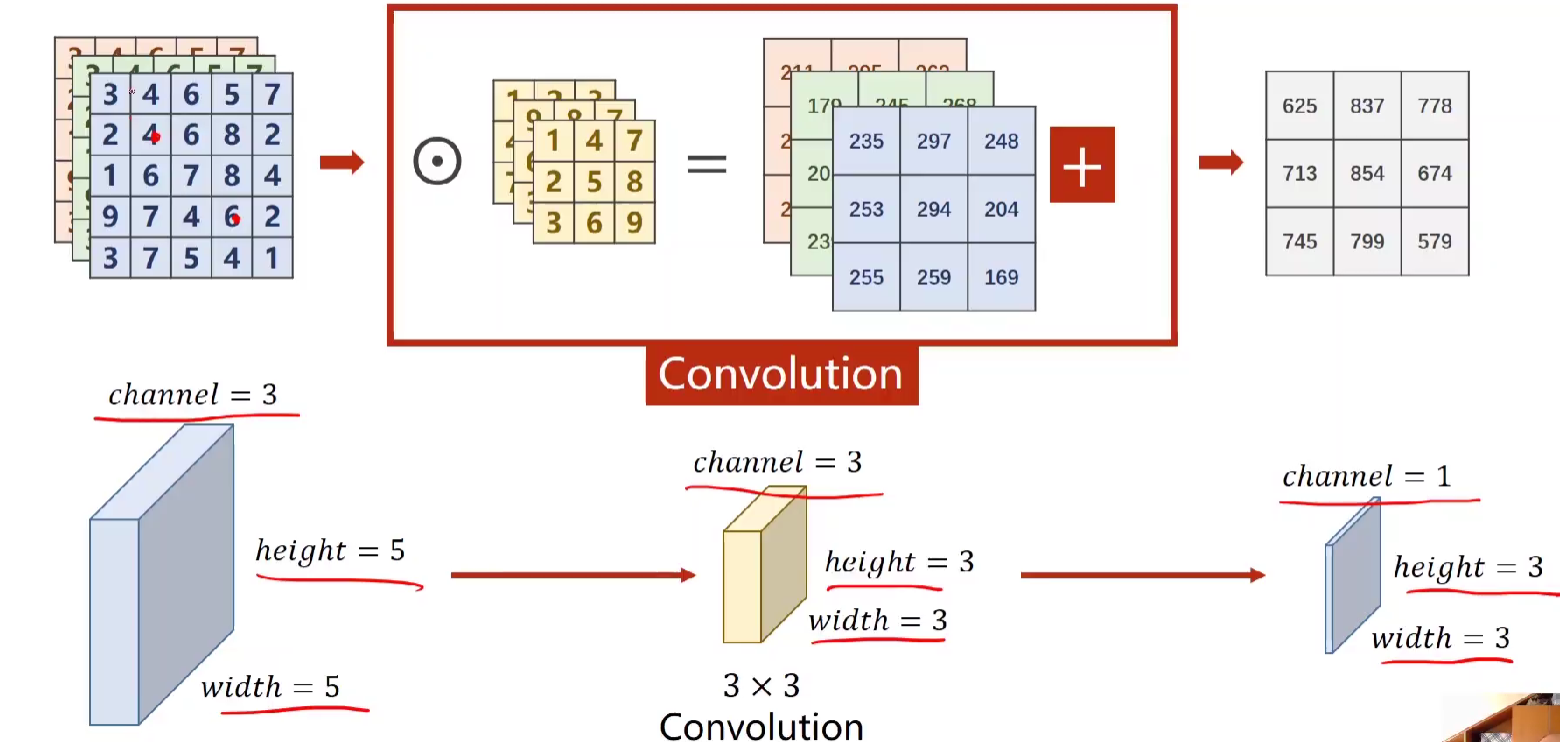
- 将上述的几个摞起来成为块,那么就分别是3*3*3的patch和一个用卷积核摞起来的3*3*3的块进行数乘后求和,即下图
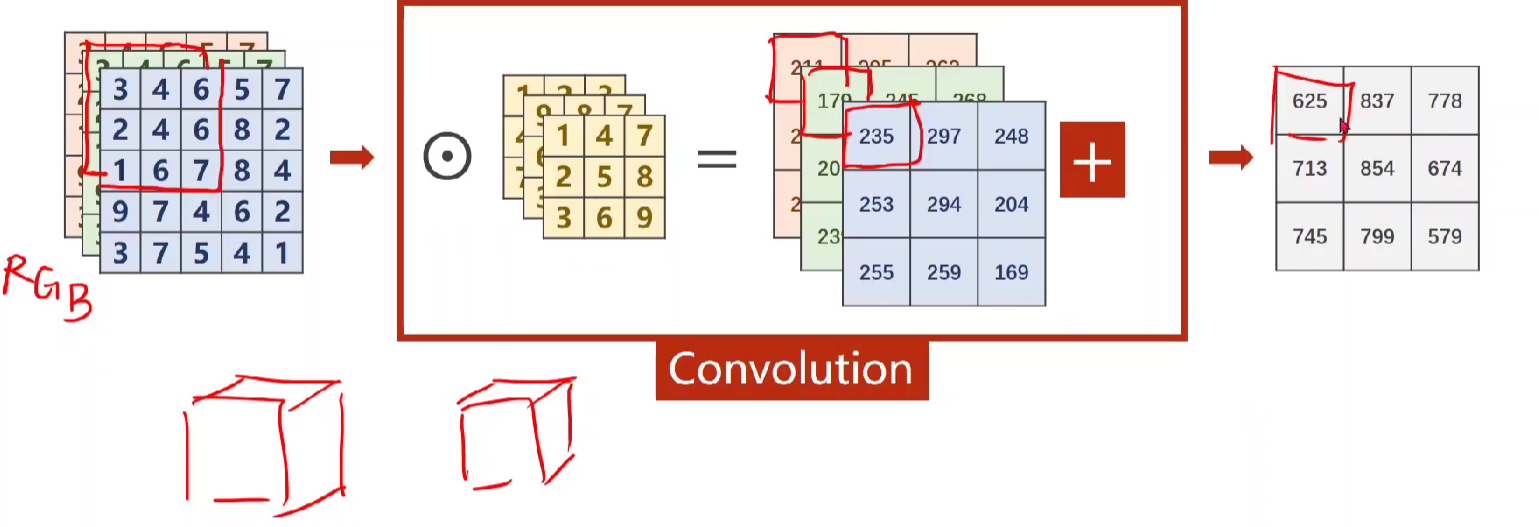
- 实现下图,由三通道变为单通道,且W、H均改变。
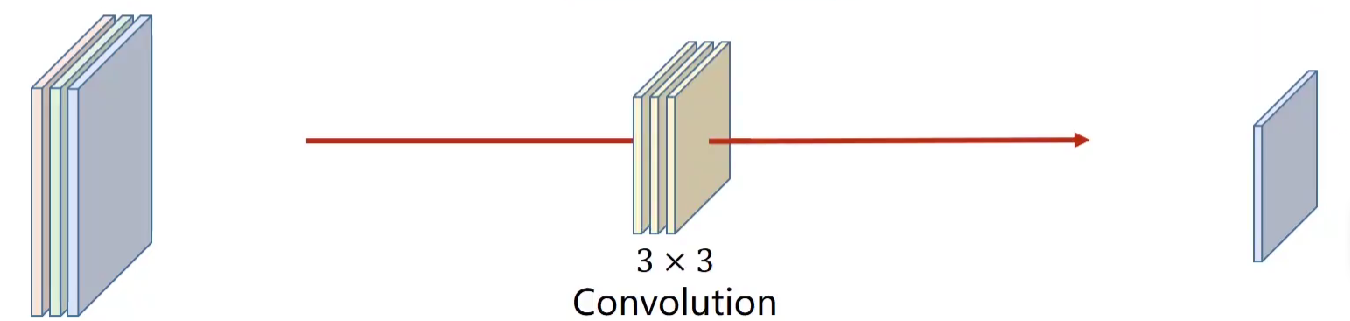
如下图,因为是做3*3的卷积,由左上角的中心点可得出会少掉两行两列
有个公式:output的W、H = input的W、H - kernel_size + 1 (例如在这里5-3+1=3
♦输入N个channel,得到M 个channel
由上面易得,一个input为N*W*H,在通过一个卷积核N*W'H'后变成了1*W'*H'的map。
因此若要m个通道,就用m个卷积核,再将所有得到的一个channel摞起来。
规律:(1)每一个卷积核的通道数量与输入的通道数量相同。 (2)输出的通道数与卷积核个数相同。
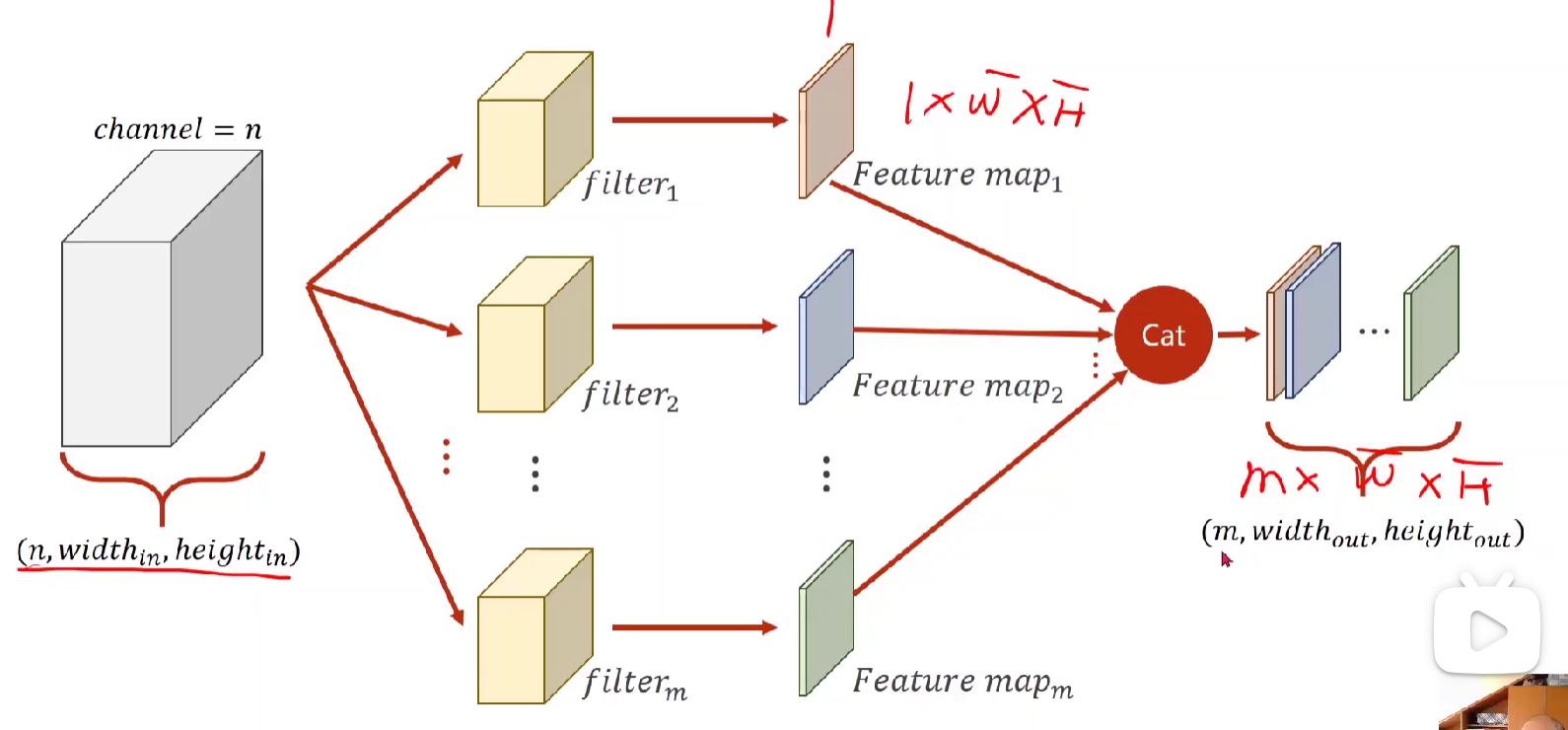
四维张量,m个n通道w宽度h高度的相同的卷积核。

代码:
import torch in_channels,out_channels = 5,10 width,height = 100,100#图像大小 kernel_size = 3#卷积核大小 batch_size = 1 input = torch.randn(batch_size,in_channels,width,height)#小批量的batch conv_layer = torch.nn.Conv2d(in_channels,out_channels,kernel_size=kernel_size) output = conv_layer(input) print(input.shape) print(output.shape) print(conv_layer.weight.shape)#卷积核权重,10个5*3*3,其实就是前面提到的m*n*w*h>>
torch.Size([1, 5, 100, 100])
torch.Size([1, 10, 98, 98])
torch.Size([10, 5, 3, 3])
卷积层——Padding填充
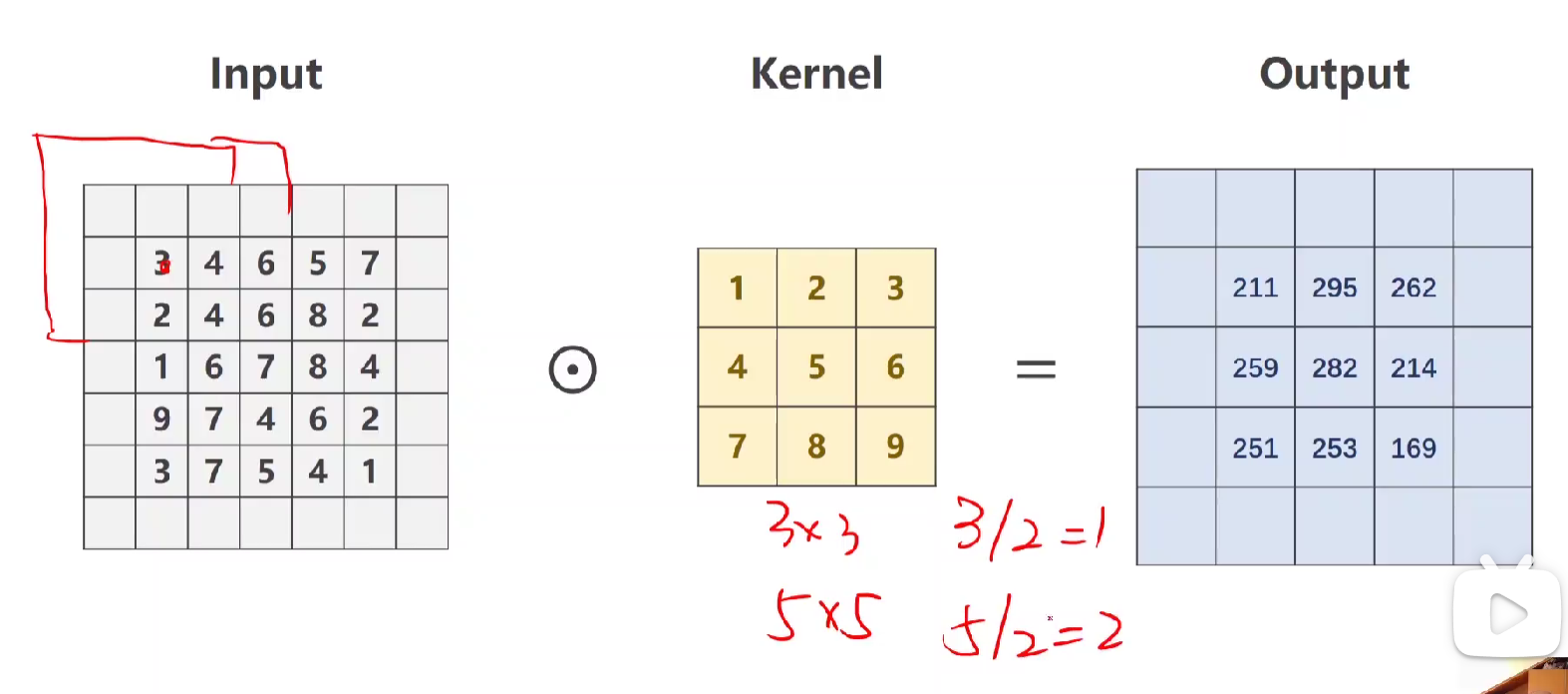
若要输出和输入的W、H相同,就用填充。如上图,若卷积为3*3就填1,5*5就填2
公式为:kernel_size / 2
得到结果如下图:
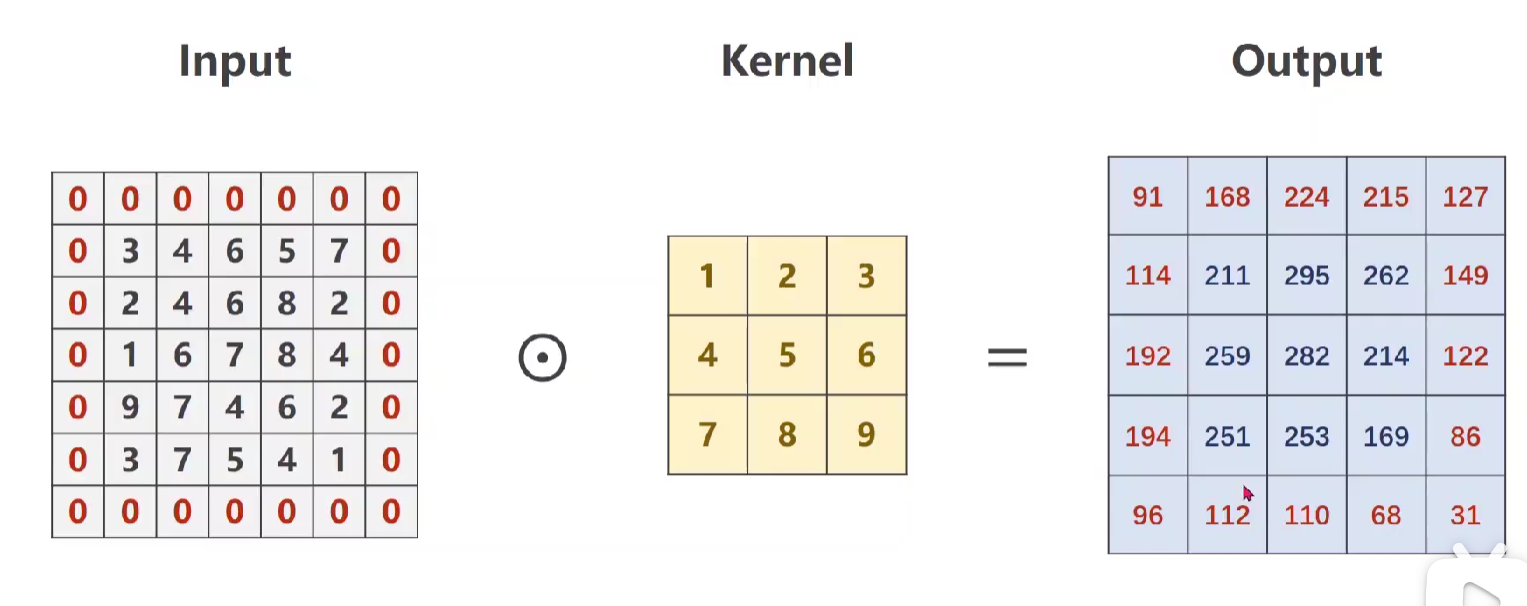
下面是关于上述padding的例子代码实现:【注意:在下面代码加粗部分可以看到bias=False,可以说明卷积其实也是一种线性运算,这也为后面卷积神经网络中加了激活函数做铺垫,进行非线性运算。】
import torch input = [3,4,5,6,7, #输入的图像 2,4,6,8,2, 1,6,7,8,4, 9,7,4,6,2, 3,7,5,4,1] input = torch.Tensor(input).view(1,1,5,5) #reshape一下,batch,in_channel,w,h #初始化这个卷积,规定out_channel,in_channel,kernel_size,是否填充 #这里padding = 1,即行列各加一 #注意bias conv_layer = torch.nn.Conv2d(1,1,kernel_size=3,padding=1,bias=False) kernel = torch.Tensor([1,2,3,4,5,6,7,8,9]).view(1,1,3,3)#O, I, W, H,卷积的权重定义 conv_layer.weight.data = kernel.data output = conv_layer(input) print(output)>>
tensor([[[[ 91., 162., 225., 216., 131.],
[114., 208., 296., 263., 150.],
[192., 259., 282., 214., 122.],
[194., 251., 253., 169., 86.],
[ 96., 112., 110., 68., 31.]]]], grad_fn=<ThnnConv2DBackward0>)
卷积层——stride步长
作用:有效降低图像的宽度和高度。
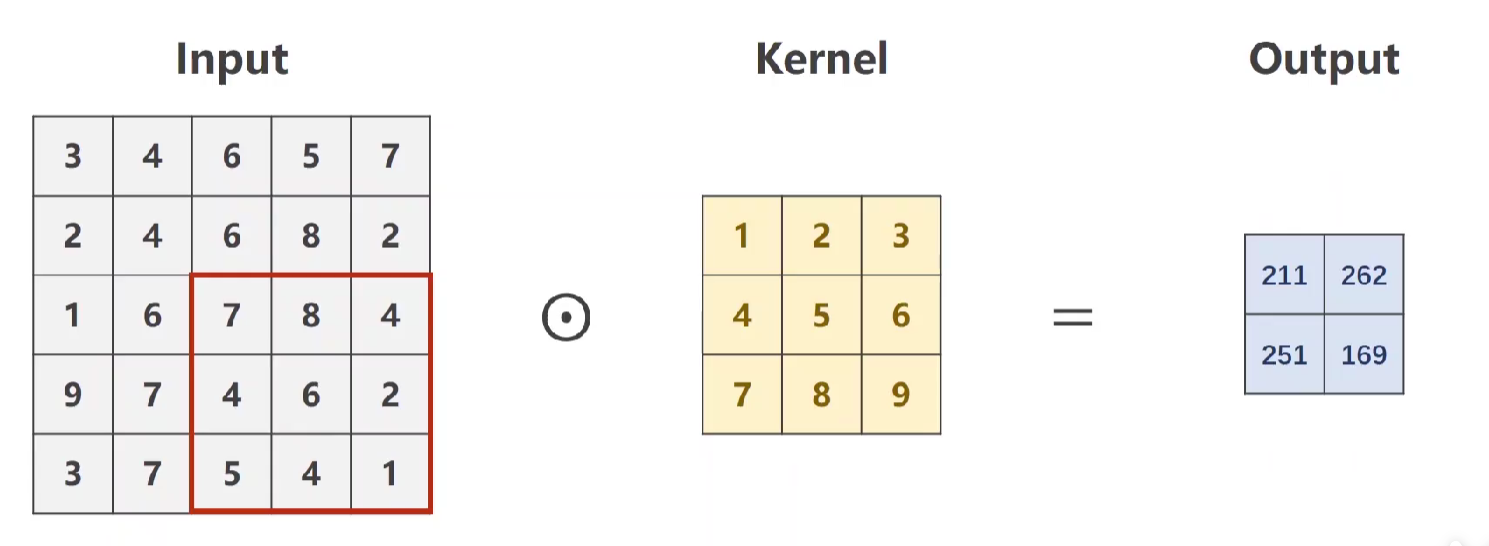
代码实现:
import torch input = [3,4,5,6,7, #输入的图像 2,4,6,8,2, 1,6,7,8,4, 9,7,4,6,2, 3,7,5,4,1] input = torch.Tensor(input).view(1,1,5,5) conv_layer = torch.nn.Conv2d(1,1,kernel_size=3,stride=2,bias=False) kernel = torch.Tensor([1,2,3,4,5,6,7,8,9]).view(1,1,3,3) conv_layer.weight.data = kernel.data output = conv_layer(input) print(output)>>
tensor([[[[208., 263.],
[251., 169.]]]], grad_fn=<ThnnConv2DBackward0>)
下采样
♦ Max Pooling Layer最大池化层(信息存在丢失的情况)
特点:是对一个通道做Max pooling, 而不是通道之间,所以通道数不变。下图用2*2做MxaPooling,图像缩为原来的一半。
没有权重,是一种采样方式。用2*2的maxpooling,stride=2 ,扔掉了一半的特征,但是减少了卷积的操作,速度更快。
注意注意:Maxpooling如果没有指定stride的值,会默认等于maxpooling的值! (类似这里maxpooling=2所以默认为2)
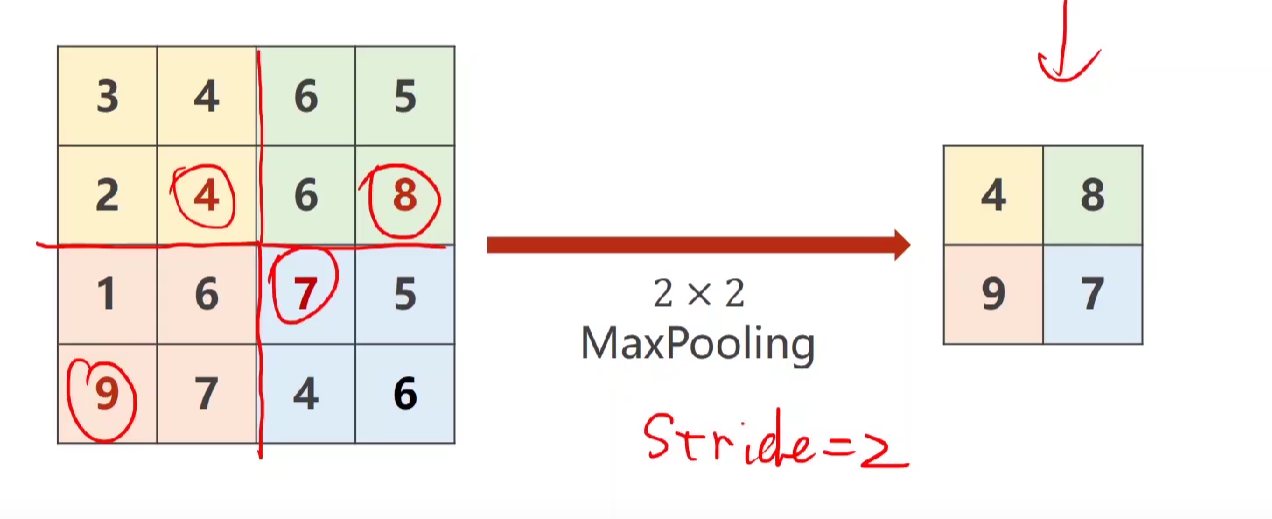
下面举一个简单的卷积神经网络
卷积——>最大池化——>到最后需要做一个view,将(batch20*4*4)->(batch,320)——>然后单纯做一个全连接层,将320直接降到十维
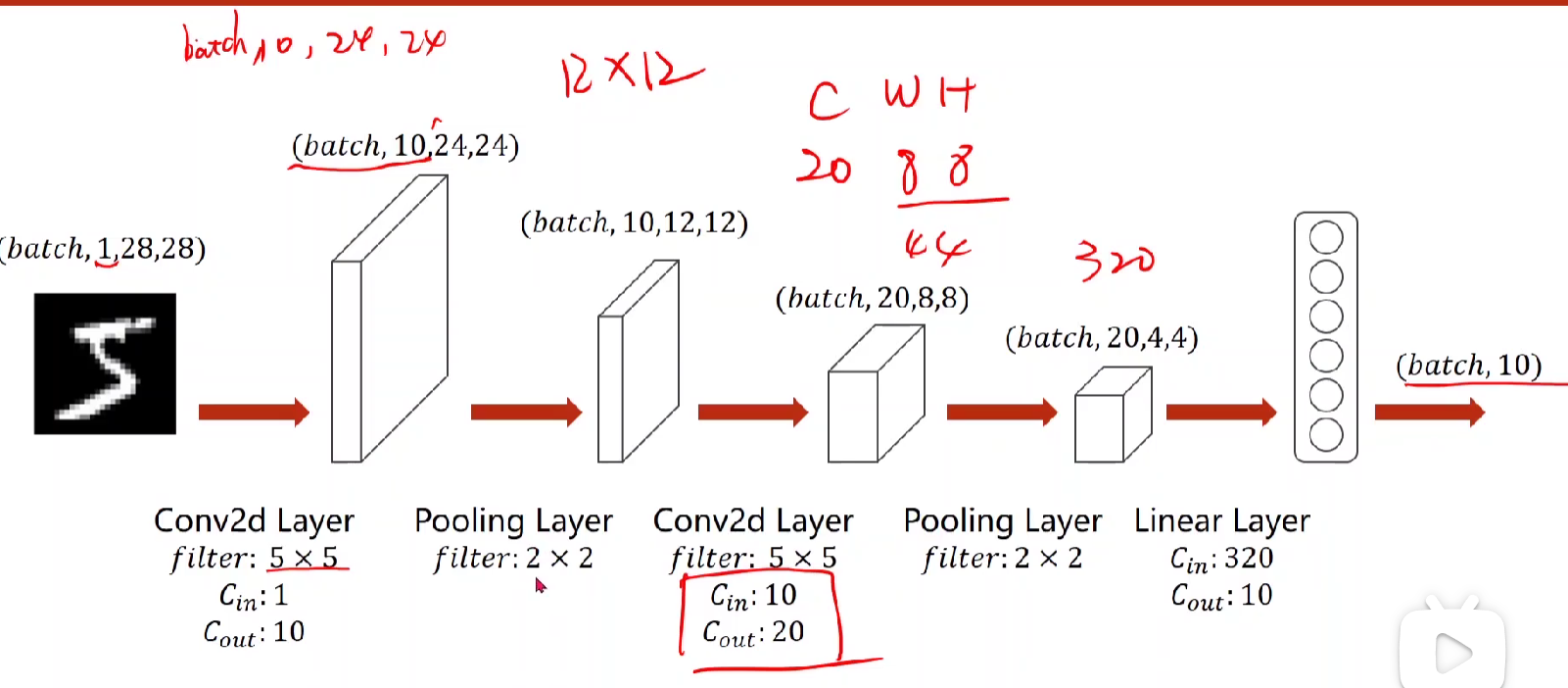
最后的维度查看用print
okook重头戏来咯,之前MNIST用的是全连接神经网络,现在活学活用一下,用卷积神经网络
在这里解释一些可能会困惑的点吧:
1.做卷积是因为我们如果单纯的用前面的linear layer会导致空间特征没办法保留。
2.在这里卷积之后的进行激活是因为做卷积运算本身是让图像乘权重,本质上是一种线性变换,而我们通过激活加入非线性因子可以解决一些线性无法解决的问题(联想之前线性输出的值没法对应分类,而激活后映射到了[0,1] / [-1,1]后就可以通过这个概率解决分类问题)。
3.最后要用view将(batch20*4*4)->(batch,320),从而便于后面直接用全连接层降到十维,对应分类。
4.降到十维之后的输出与图像分类的输出有对应,就可以扔到交叉熵损失进行训练咯(所以可以看到最后一层不用做激活,直接扔CrossEntropyLoss)
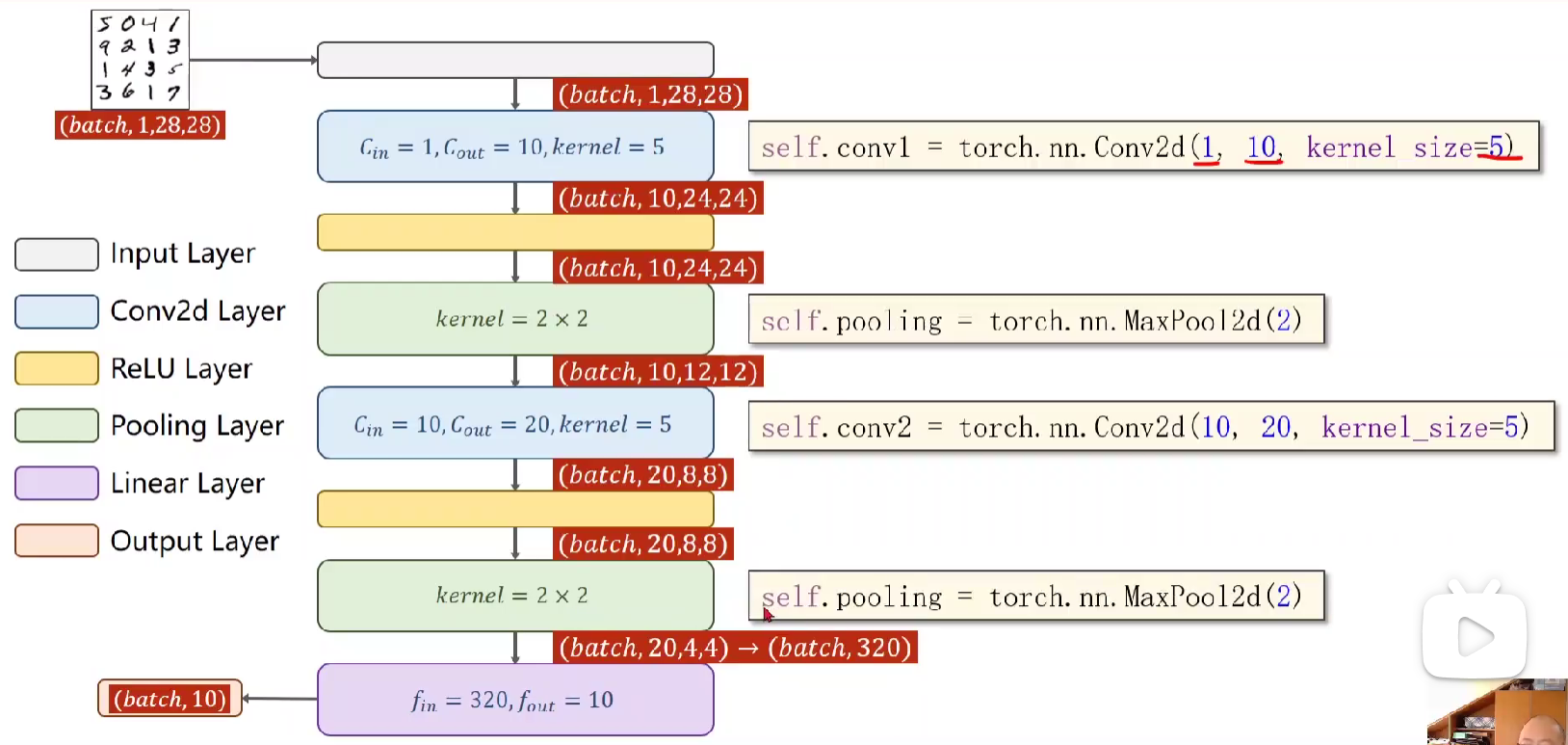
下面是具体代码(其实跟之前全连接层不一样的也就是model了,其他都一样)
import torch import numpy as np from torch.utils.data import Dataset #抽象类,只能由子类来继承 from torch.utils.data import DataLoader #可实例化 filepath = 'C:\\Users\\jiwenting\\Desktop\\diabetes.csv' class DiabetsDataset(Dataset): #自定义类 #魔法 def __init__(self,filepath): xy = np.loadtxt(filepath,delimiter=',',dtype=np.float32) self.len = xy.shape[0] #用shape[0]输出行的数目,即N self.x_data = torch.from_numpy(xy[:,:-1]) #x_data为前八列 self.y_data = torch.from_numpy(xy[:,[-1]]) #y_data为最后一列 def __getitem__(self, index) : #通过索引调出数据 return self.x_data[index],self.y_data[index] def __len__(self): return self.len dataset = DiabetsDataset(filepath) #通过自定义类实例化 #传入定义的数据集,然后输入 batch_size 和 shuffle 来进行loader; 而num-wokers表示几个并行的进程来读取mini_batch的数据 train_loader = DataLoader(dataset=dataset,batch_size=32,shuffle=True,num_workers=0) #model class Model(torch.nn.Module): def __init__(self) -> None: super(Model,self).__init__() self.linear1 = torch.nn.Linear(8,6)#构造对象,八维到六维 self.linear2 = torch.nn.Linear(6,4) self.linear3 = torch.nn.Linear(4,1) self.activate = torch.nn.Sigmoid() def forward(self,x): x = self.activate(self.linear1(x)) x = self.activate(self.linear2(x)) x = self.activate(self.linear3(x)) return x model = Model() #loss & optimizer criterion = torch.nn.BCELoss(reduction='mean') optimzer = torch.optim.SGD(model.parameters(),lr=0.01) #training circle if __name__ == '__main__': for epoch in range(100): #一整批的数据都跑完一次叫做一个epoch ''' 用enumerate获得当前为第几次迭代,0为起始位置 :直接对train_loader做迭代 从train_loader拿出Dataset自己实现的__getitem__的返回值即(x,y)元组放入data中 在这里loader自动的把xy构成的矩阵转化为Tensor类型的计算图,所以直接传进去就好了 ''' for i,(input,labels) in enumerate(train_loader,0): #forward y_pred = model(input) loss = criterion(y_pred,labels) print(epoch,i,loss.item()) optimzer.zero_grad() loss.backward() optimzer.step() device = torch.device("cuda=0"if torch.cuda.is_available() else "cpu")
结果:可以看到这里比之前上涨了1%,ok接下来就是老科研角度,从出错角度看3%到2%,降了1/3啊!牛不牛吧就说!
另外如果有显卡要用GPU跑的话要加上
device = torch.device("cuda:0"if torch.cuda.is_available() else "cpu")
#然后就是按照视频里在对应模块分别丢入device
这里就是说如果有显卡就返回True执行“cuda=0”,当然如果电脑有很多显卡就指定呗。如果没有显卡就返回False执行“gpu”
作业:
在这里提一嘴




 浙公网安备 33010602011771号
浙公网安备 33010602011771号