贪心算法基础练习笔记
贪心算法也是一种优化多阶段决策问题的策略,贪心算法在问题的每个阶段总是作出在当前看来最好的选择。也就是说贪心算法并不从整体最优考虑,它所作出的选择只是在某种意义上的局部最优选择。对于某些问题贪心算法得到的最终结果也是整体最优的。在一些情况下,即使贪心算法不能得到整体最优解,其最终结果却是最优解的非常近似解。
适用范围:
贪心选择性质:所谓贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到。这是贪心算法可行的第一个基本要素,也是贪心算法与动态规划算法的主要区别。
最优子结构性质:当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用动态规划算法或贪心算法求解的关键特征。
贪心算法与动态规划算法的差异:贪心算法和动态规划算法都要求问题具有最优子结构性质,这是2类算法的一个共同点。但是,对于具有最优子结构的问题应该选用贪心算法还是动态规划算法求解?是否能用动态规划算法求解的问题也能用贪心算法求解?
动态规划算法通常以自底向上的方式解各子问题,而贪心算法则通常以自顶向下的方式进行,以迭代的方式作出相继的贪心选择,每作一次贪心选择就将所求问题简化为规模更小的子问题。
对于一个具体问题,要确定它是否具有贪心选择性质,必须证明每一步所作的贪心选择最终导致问题的整体最优解。
【例1】最多装载:有一批集装箱要装上一艘载重量为 c 的轮船。其中集装箱 i 的重量为 Wi。要求确定在装载体积不受限制的情况下,将尽可能多的集装箱装上轮船。
把物品按重量升序,先装重量小的,就可以尽可能多装。

1 /**装载问题-贪心算法
2 * @param w 集装箱重量
3 * @param c 船的装载容量
4 * T(n)=O(n),S(n)=O(n)
5 */
6 private static void greedyLoading(int[] w,int c){
7 //把集装箱重量升序
8 Arrays.sort(w);
9 //记录装入物品
10 ArrayList<Integer> optimal = new ArrayList<>();
11 //当前轮船的装载量
12 int cw = 0;
13 //物品编号
14 int i = 0;
15 while ((cw + w[i]) <=c ){
16 optimal.add(w[i]);
17 cw+=w[i];
18 i++;
19 }
20 System.out.println("最优值:"+optimal.size());
21 System.out.println("最优解:"+optimal);
22 }
【例2】活动安排问题:设有 n 个活动的集合E = {1, 2, …, n},其中每个活动都要求使用同一资源,如演讲会场等,而在同一时间内只有一个活动能使用这一资源。每个活动i都有一个要求使用该资源的起始时间 si 和一个结束时间 fi,且 si < fi 。如果选择了活动 i,则它在半开时间区间[si, fi)内占用资源。若区间[si, fi)与区间[sj, fj)不相交,则称活动 i 与活动 j 是相容的。也就是说,当si ≥ fj或 sj ≥ fi 时,活动 i 与活动 j 相容。求最多安排几个活动以及具体的活动选择和顺序。
实例:
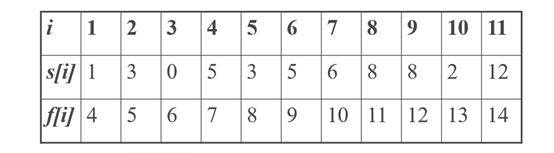
对于每一个阶段,当前最优选择就是与前面的活动不冲突的情况下最早结束的活动,因为这样才能给后面的活动留更多时间以安排更多的活动。
先把所有活动按结束时间从早到晚排序,对于每一个活动,只要开始时间不早于上一个活动的完成时间,就加入安排列表。
代码实现:

1 public static void main(String[] args) {
2 int[][] acticity = {{1,1,4},{2,3,5},{3,0,6},{4,5,7},{5,3,8},
3 {6,5,9},{7,6,10},{8,8,11},{9,8,12},{10,2,13},{11,12,14}};
4 activityArrangement(acticity);
5 }
6 /** 活动安排-贪心算法
7 * @param activity 活动数据 [i][0]是编号,[i][1]是开始时间,[i][0]是结束时间
8 * T(n)=O(n),S(n)=O(n)
9 */
10 private static void activityArrangement(int[][] activity){
11 //把所有活动按结束时间f从早到晚排序
12 Arrays.sort(activity, Comparator.comparingInt(o -> o[2]));
13 //记录上一活动结束时间
14 int endT = 0;
15 //按顺序记录安排好的活动编号
16 ArrayList<Integer> scheduleList = new ArrayList<>();
17 for (int[] ac : activity) {
18 //如果当前活动开始时间不早于上一个活动结束时间,就加入安排列表
19 if (ac[1] >= endT) {
20 scheduleList.add(ac[0]);
21 //更新结束时间
22 endT = ac[2];
23 }
24 }
25 System.out.println("最优值:"+scheduleList.size());
26 System.out.println("最优解:"+scheduleList);
27 }
【例3】背包问题:给定 n 种物品和一个背包。物品 i 的重量是 Wi,其价值为 Vi,背包的容量为 C。应如何选择装入背包的物品,使得装入背包中物品的总价值最大?背包问题要求每种物品可放入一部分。
实例:n=10,c=20,w={7,5,6,9,12,4,2,8,11,15},v={15,10,35,20,45,25,30,50,5,40}
先把物品按单位重量价值降序,然后按顺序放入背包,最后一个如果只能放一部分就按比例计算价值。

1 public static void main(String[] args) {
2 int[][] acticity = {{1,7,15},{2,5,10},{3,6,35},{4,9,20},{5,12,45},
3 {6,4,25},{7,2,30},{8,8,50},{9,11,5},{10,15,40}};
4 int c = 20;
5 knapsack(acticity,c);
6 }
7 /**背包问题-贪心算法
8 * @param goods [i][0]是物品编号,[i][1]是物品重量,[i][0]是物品价值
9 * @param c 背包容量
10 * T(n)=O(n),S(n)=O(n)
11 */
12 private static void knapsack(int[][] goods,int c){
13 //把所有物品按单位价值降序
14 Arrays.sort(goods, (o1, o2) -> o2[2]/o2[1]-o1[2]/o1[1]);
15 //记录当前背包的剩余容量
16 int currW = c;
17 //记录当前背包的物品价值
18 int currV = 0;
19 //按顺序记录放入背包物品编号
20 ArrayList<Integer> goodsList = new ArrayList<>();
21 //判断最后一个物品是否完整
22 boolean entire = true;
23 for (int[] g : goods) {
24 //如果当前物品能放入背包就直接放入
25 if (g[1] <= currW) {
26 goodsList.add(g[0]);
27 currW = c-g[1];
28 currV += g[2];
29 }else {
30 //否则放入一部分,按重量比例计算价值
31 currV += g[2]*currW/g[1];
32 goodsList.add(g[0]);
33 entire = false;
34 break;
35 }
36 }
37 System.out.println("最优值:"+currV);
38 System.out.println("最优解:"+goodsList);
39 if (!entire){
40 System.out.println("最后一个物品只放入一部分");
41 }
42 }
【例4】单源最短路径:给定带权有向图 G = (V, E),其中顶点集合为V,边集合为E,每条边的权是非负实数。另外,还给定 V 中的一个顶点,称为源。现在要计算从源到所有其他各顶点的最短路长度。这里路的长度是指路上各边权之和。这个问题通常称为单源最短路径问题。(Dijkstra算法)
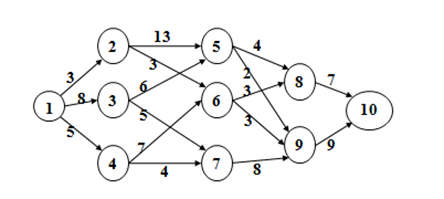
先设一个集合S,当找到从源点s到某点x的最短距离时,把x点放入S中,初始时S只有源点,当所有点都放入S中时求出问题的结果。设一个数组d记录每个点到源点的距离,初始时都为无穷大。设当前要搜索的点为p,初始时p=s,先遍历边集合E,找到从p直达的点E[p][i],把对应点到源点的距离记录到数组d中,然后遍历d找到距离最小且不在S中的点a,可以确定a到源点的最近距离已经找到了,因为通过其他点到a点的距离只会更大,把a放入S。因为问题具有贪心选择性质,所以p=a,循环执行上述操作就能确定下一个点的最短路径,直到所有点都放入S算法结束。

1 public static void main(String[] args) {
2 //点数
3 int n = 10;
4 //边的权值
5 int[][] edge = new int[n+1][n+1];
6 edge[1][2] = 3; edge[1][3] = 8; edge[1][4] = 5;
7 edge[2][5] = 13; edge[2][6] = 3;
8 edge[3][5] = 6; edge[3][7] = 5;
9 edge[4][6] = 7; edge[4][7] = 4;
10 edge[5][8] = 4; edge[5][9] = 2;
11 edge[6][8] = 3; edge[6][9] = 3;
12 edge[7][9] = 8;edge[8][10] = 7;edge[9][10] = 9;
13 //选一个源点
14 int sourcePoint = 1;
15 getRoute(edge,sourcePoint,n);
16 }
17 private static void getRoute(int[][]edge,int sourcePoint,int n){
18 //当前要搜索的点
19 int currPoint = sourcePoint;
20 //途经点集
21 ArrayList<Integer> s = new ArrayList<>();
22 //判断某点是否已经确定
23 boolean[] bool = new boolean[n+1];
24 //记录源点到其他点的距离
25 int[] dist = new int[n+1];
26 //循环n次每次确定一个点到源点的最近距离
27 for (int i = 1; i <= n; i++) {
28 //初始化 所有点间距为无限大
29 dist[i]=Integer.MAX_VALUE;
30 }
31 //源点距离为0
32 dist[sourcePoint] = 0;
33 //源点放入s[]并确定
34 bool[sourcePoint]=s.add(currPoint);
35 for (int i = 0; i < n; i++) {
36 //遍历边数组
37 for (int j = 1; j <=n ; j++) {
38 //找到当前点cp直接相距点,放入s[]的点除外
39 if (edge[currPoint][j]!=0&&!bool[j]) {
40 //记录源点经过当前点到i点的距离,因为能到i点的点不止一个,当前点到i点不一定最近,所以先判断大小再赋值
41 dist[j]=Math.min(dist[j],dist[currPoint]+edge[currPoint][j]) ;
42 }
43 }//工具变量
44 int a=Integer.MAX_VALUE, b=0;
45 //遍历dist数组,找出距端点最近并且不在s集中的点b,则b点到源点最近距离已确定
46 for (int j = 1; j <= n; j++) {
47 if (dist[j] < a && !bool[j]){
48 a=dist[j];b=j; }
49 }//把b点放入s集并确定
50 bool[b] = s.add(b);
51 //更新当前搜索点
52 currPoint=b;
53 }//打印每个点到源点的最近距离
54 System.out.println(Arrays.toString(dist));
55 }
【例5】最小生成树:设G = (V, E)是无向连通带权图,即一个网络。E中每条边(v, w)的权为c[v][w]。如果 G 的子图 G' 是一棵包含 G 的所有顶点的树,则称 G' 为 G 的生成树。生成树上各边权的总和称为该生成树的耗费。在 G 的所有生成树中,耗费最小的生成树称为 G 的最小生成树。(Prim算法和Kruskal算法)
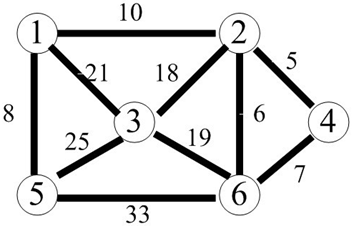
V[]={1,2,3,4,5,6}
E[][]={
{0, 0, 0, 0, 0, 0, 0},
{0, 0,10,21, 0, 8, 0},
{0,10, 0,18, 5, 0, 6},
{0,21,18, 0, 0,25,19},
{0, 0, 5, 0, 0, 0, 7},
{0, 8, 0,25, 0, 0,33},
{0, 0, 6,19, 7,33, 0}}
Prim加点法:
设一个一维数组S记录最小生成树的点,设一个二维数组T记录最小生成树的边。先随机从V选一点添加到S,S={0,3}。然后在E中找出i∈S,j∈V-S,且权重E[i][j]最小的边(i,j)。最后把j点添加到S,S={0,1,j},把边的权重记录到T,T[i][j]=E[i][j],循环执行这个过程直到S=V时结束。此时T中所有的边构成G的最小生成树。
Kruskal加边法:
设一个二维数组T记录最小生成树的边。首先把G图的每个点当成一个子树的根节点,设一个一维数组S记录每个点对应的子树编号,S={0,1,2,3,4,5,6,7}。遍历E数组把G图的每条边按权重从小到大排序,设一个二维数组K按顺序记录所有边对应的点和权重,例如最短的边是(1,2),权重是1,记作K[1]={1,2,1}。然后从K[1]开始按权重递增顺序查看每一条边,当查看第i条边时,如果其连接的两个点K[i][0]和K[i][1]不在同一子树:S[K[i][0]]≠S[K[i][1]],就用这条边连接这两颗子树:遍历S,如果S[i]=S[K[i][0]],则S[i]=S[K[i][1]]。同时确定这条边为最小生成树的一条边:T[K[i][0]] [K[i][1]]=K[i][2]。否则就跳过这条边。循环这个过程直到所有点都在同一子树时结束。此时T中所有的边构成G的最小生成树。

1 public static void main(String[] args) {
2 //点数
3 int n = 6;
4 //无向图G的顶点集合v
5 int[] vertex = new int[n+1];
6 //无向图G的边集合E
7 int[][] edge = new int[n+1][n+1];
8 //最小生成树MST的边集合,点集不用变。
9 int[][] mstEege = new int[n+1][n+1];
10 inputGraph(vertex,edge,mstEege);//输入图数据
11 kruskal(edge,mstEege);//计算最小生成树的边
12 int weightOfMST = 0;//最小生成树的总权重
13 System.out.println("最小生成树为:");
14 for (int i = 1; i <= n; i++) {
15 ArrayList<Integer> arr = new ArrayList<>();
16 for (int j = 1; j <= n; j++) {
17 if (mstEege[i][j]!=Integer.MAX_VALUE && i<j){
18 weightOfMST +=mstEege[i][j];
19 arr.add(j);
20 }
21 }
22 if (arr.size()!=0) {
23 System.out.println(i+"———"+arr);
24 }
25 }
26 System.out.println("最小生成树的总权重为:"+ weightOfMST);
27 }
28 private static void inputGraph(int[] vertex,int[][] edge,int[][] mstEege){
29 for (int i = 0; i < 7; i++) {
30 vertex[i] = i;//输入G图点数据
31 for (int j = 0; j < 7; j++) {
32 edge[i][j] = Integer.MAX_VALUE;//G图的边初始化
33 mstEege[i][j] = Integer.MAX_VALUE;//MST的边初始化
34 }
35 }
36 //输入边数据
37 edge[1][2]=10; edge[2][1]=10; edge[1][3]=21; edge[3][1]=21;
38 edge[1][5]=8; edge[5][1]=8; edge[2][3]=18; edge[3][2]=18;
39 edge[2][4]=5; edge[4][2]=5; edge[2][6]=6; edge[6][2]=6;
40 edge[3][5]=25; edge[5][3]=25; edge[3][6]=19; edge[6][3]=19;
41 edge[4][6]=7; edge[6][4]=7; edge[5][6]=33; edge[6][5]=33;
42 }
43 private static void prim (int n,int[] vertex,int[][] edge,int[][] mstEege){//加点法
44 int[] node = new int[n+1];//临时点集
45 boolean bool [] = new boolean[n+1];//判断是结点是否确定
46 node[1] = vertex[5];//在vertex中随便选个点放入node[1]作为第一个点
47 bool[5] = true;
48 for (int i = 2; i <= n; i++) {
49 /*最小生成树剩下5个节点未确定,每次循环确定一个点,依次放入node[i],所以i要从2开始*/
50 int e = Integer.MAX_VALUE;//记录当前最小的边的值
51 int a = 0;//记录node中与当前最小边相连的点
52 int b = 0;//记录与当前最小边相连的另一点,要求在vertex中且不在node中。
53 for (int j = 1; j <= n; j++) {//遍历vertex中的所有点
54 if (node[j]!=0) {//找到node里的点node[j]
55 //再遍历vertex中的所有点找到所有与node[j]直接相连的点
56 for (int k = 1; k <= n; k++) {
57 //找到最小边edge[node[j]][k]以及距离node[j]最近的点k
58 if (edge[node[j]][k]<e && !bool[k]){
59 e = edge[node[j]][k];//记录当前最小边以及对应点node[j]和K
60 a = node[j];
61 b = k;
62 }
63 }
64 }
65 }
66 node[i] = b;//把距node中某点最近的点放入node
67 bool[b] = true;
68 mstEege[a][b] = e;//记录MST的一条边
69 mstEege[b][a] = e;
70 }
71 }
72 private static void kruskal(int n,int[][] edge,int[][] mstEege){//加边法
73 /*初始时每个点作为根节点分别构成一个子树,
74 subtree[i]表示第i号结点所在的子树*/
75 int[] subtree = new int[n+1];
76 boolean bool [][] = new boolean[n+1][n+1];//判断边是否确定
77 for (int i = 0; i <= n; i++) {
78 subtree[i] = i;//输入每个子树根节点
79 } //最小生成树剩下n-1条边未确定,每次循环确定一条放入tree
80 for (int i = 0; i < n-1; i++) {
81 int e = Integer.MAX_VALUE;//记录当前最小的边的权重
82 int a = 0;//记录当前最小边相连的两个点
83 int b = 0;
84 for (int j = 1; j <= n; j++) {
85 for (int k = 1; k <= n; k++) {
86 //找到最小边edge[j][k],要求该边连接的两个点j和k不在同一子树上
87 if (edge[j][k]<e && !bool[j][k] &&subtree[j]!=subtree[k]){
88 e = edge[j][k];//记录当前最小边以及对应的点j和k
89 a = j;
90 b = k;
91 }
92 }
93 }
94 for (int j = 1; j <= n; j++) {
95 if (subtree[j] == b) {
96 subtree[j] = subtree[a];//合并子树
97 }
98 }
99 bool[a][b] = true;//确定一条边
100 bool[b][a] = true;
101 mstEege[a][b] = e;//记录MST的一条边
102 mstEege[b][a] = e;
103 }
104 }
【例6】多机调度问题:要求给出一种作业调度方案,使所给的 n 个作业在尽可能短的时间内由 m 台机器加工处理完成。每个作业均可在任何一台机器上加工处理,但未完工前不允许中断处理。作业不能拆分成更小的子作业。
实例:设 9 个独立作业由 4 台机器 M1,M2,M3 和 M4加工处理。各作业所需的处理时间分别为{2, 14, 4, 16, 6, 5, 3, 17, 12}。
算法思路:首先把所有作业按加工时间降序排列,让耗时最长的作业先加工。然后把所有机器按剩余加工时长升序排列,让活最少的机器先安排作业。每安排一个作业,都要重新给机器排序。
伪代码:
int[] mT 记录每个机器任务量(时长)
int[] pT {2, 14, 4, 16, 6, 5, 3, 17, 12}每个作业时长
pT 降序
for(i=0,i<12,i++){
mT[0]=pT[i] 让活最少的机器先安排作业
mT升序
}

1 public static void main(String[] args) {
2 int n = 9;
3 int m = 4;
4 //各机器工作时间
5 int[] machiningT = new int[m];
6 //各作业所需的处理时间
7 Integer[] processingT = {2,14,4,16,6,5,3,17,12};
8 //作业降序
9 Arrays.sort(processingT, Collections.reverseOrder());
10 for (int i = 0; i < n; i++) {
11 //安排当前作业
12 machiningT[0]+=processingT[i];
13 //机器升序
14 Arrays.sort(machiningT);
15 }
16 //打印活最多的机器的完成时间
17 System.out.println(machiningT[0]);
18 }
【例7】

思路:遍历汽车的最大行驶范围(满油箱可行驶的距离)内的所有加油站,找到比当前站更便宜且最近的加油站,同时记录范围内最远的加油站,
如果范围内有更加便宜的加油站就在当前站加最少的油开过去,如果范围内没有更便宜的加油站先判断终点在不在范围内,如果在就加刚好能
到终点的油,如果不在就在当前加油站加满油行驶到最远的加油站

1 import java.text.DecimalFormat;
2 public class Trival {
3 public static void main(String[] args) {
4 double cityD = 1000;//两城市的距离(km)
5 double tankC = 40;//油箱容量(L)
6 double cPetrol = 10;//当前油量
7 double sPetrol = 7.51;
8 double pConsumption = 20;//耗油量(km/L)
9 //gasStation[i]表示第i个加油站的油价(¥/L)和距前一个加油站的距离(km)
10 double[][] gasStation = {{sPetrol,0},{7.25,156},{7.69,365},{7.22,572},{7.77,702},{7.35,895},{0,cityD}};
11 double[] plan = refuelingPlan(tankC,cPetrol,pConsumption,gasStation);
12 DecimalFormat df = new DecimalFormat( "0.00 ");//
13 double totalCost = 0;//
14 System.out.println("最优的加油方案为:");
15 for (int i = 0; i < plan.length; i++) {
16 if (plan[i] != 0){
17 totalCost += plan[i];
18 double rmb = plan[i]*gasStation[i][0];
19 System.out.println("在第"+i+"个加油站加"+plan[i]+"升汽油,花费"+df.format(rmb)+"元");
20 }
21 }
22 System.out.println("全程总共花费"+df.format(totalCost)+"元油钱。");
23 }
24 private static double[] refuelingPlan(double tankC,double cPetrol,double pConsumption,double[][] gasStation){
25 int cStation = 0;//当前所在的加油站的编号
26 int n = gasStation.length;//加油站数量
27 double[] plan = new double[n];//记录每个加油站分别加多少油
28 double fullTankD = tankC*pConsumption;//满油箱可行驶的距离
29 while (cStation < n-1){
30 int cheapest = cStation;//记录油箱范围内最便宜的站的编号
31 double cheapestD = 0;
32 int furthest = 0;//记录油箱范围内最远的加油站编号
33 double furthestD = 0;
34 for (int i = cStation+1; i < n; i++) {//
35 double stationD = gasStation[i][1] - gasStation[cStation][1];//到加油站i的距离
36 furthestD = stationD;
37 furthest = i;
38 if (stationD > fullTankD) break;
39 if (gasStation[i][0] <= gasStation[cStation][0] && cheapest == cStation){
40 cheapest = i;
41 cheapestD = stationD;
42 }
43 }
44 double cheapestP = cheapestD/pConsumption;
45 if (cheapest == cStation){//如果找不到更便宜的加油站就在当前站加满油
46 plan[cStation] = tankC - cPetrol;//当前站点加油量
47 cPetrol = tankC - furthestD/pConsumption;//到达更新油量
48 cStation = furthest;//更新站
49 }else if (cPetrol >= cheapestP) {//如果找到的最便宜的站比当前站就应该在当前站少加油
50 //如果当前油量能开到i就直接开过去
51 cPetrol -= cheapestP;//开到i更新当前油量
52 cStation = cheapest;//更新当前加油站
53 } else {//如果不够油就在当前加油站加到刚好能到i的油量
54 plan[cStation] = cheapestP - cPetrol;
55 cPetrol = 0;//开到i更新当前油量
56 cStation = cheapest;//更新当前加油站
57 }
58 }
59 return plan;
60 }
61 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号