网络流
基本概念
流网络
一个有向图,有一个源点( $ s $ )和一个汇点( $ t $ ),然后每一条边有一个容量( $ C(u,v) $ ),就差不多下面这个图,然后这里是不需要考虑反向边的。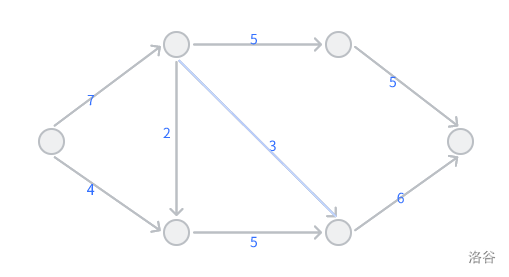
然后这里的整个图包括点集和边集,写作 $ G = (V,E) $ ,显而易见这里的 $ V $ 就是点集, $ E $ 就是边集
可行流
这里的流量用 $ f(u,v) $ 表示,然后这里也是不用考虑反向边的捏,整个可行流用 $ f $ 表示,可行流有两个条件:
- 容量限制,也就是说这一条边里面流过的流量不能超过这个边的容量
- 流量守恒:网络流的点是不能存流量的,所以对于每一个点来说,都存在着流入的量等于流出的量
用式子来表示就是:
$ \forall $ $ u ,v\in V $ $ f(u,v) \leq C(u,v) $
$ \forall $ $ u \in V $ , $ \sum f(u,v) = \sum f(v,u)$
这个可行流的流量指从源点流出的流量减流入源点的流量, $ |f| = \sum f(s,v) - \sum f(v,s) $
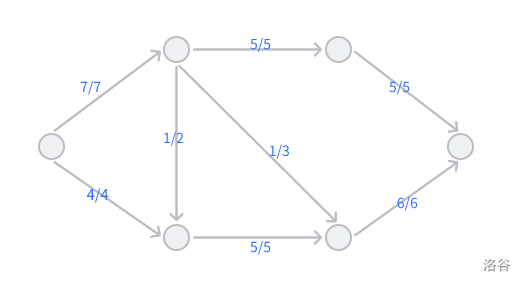
而最大流指的就是所有可行流里面流量最大的,下面就是一个可行流(好像是最大流(?),还有就是最大流不止一个捏)
残留网络
这里需要开始考虑反向边了捏。残留网络是对应原图的可行流来说的,每一个可行流都对应着一个残留网络,而残留网络中的点集 $ V' $ 和原来的流网络是一样的,边集就是原来的边集和原来边集的反向边的并集,简单理解就是原网络 - 可行流
然后残留网络每一个边对应的容量是这样的:
然后有一个结论就是残留网络的可行流 $ f' $ + 原图对应的可行流 $ f $ $ = $ 原图另一个可行流,然后这个就是上面那个可行流的残留网络
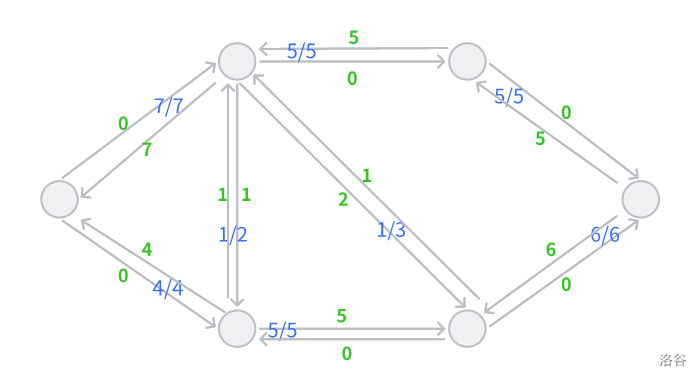
增广路径
增广路径的意思就比较简单,就是在残留网络里面,从源点出发,经过的边边权都大于 $ 0 $ ,到达汇点的路径叫做增广路径
因为由上面的残留网络的结论和增广路径的定义显然可以得到:如果一个可行流有增广路径,那么他就不是最大流,而且他的增广路径与可行流相加,所得到的可行流流量更大;反之,如果它没有增广路径,那他就是最大流,正确性显然。
所以就引出了求最大流的方法,先确定一个可行流,然后找到他的残留网络,然后看他有没有增广路径,如果有就和之前的可行流相加,再以此往复(如果错了就当这段狗叫捏)
割
一个流网络的割,就是两个点集,然后满足并起来就是 $ E $ ,交集是 $ ∅ $ ,并且源点和汇点分别在这两个集合当中。
$ S $ 和 $ T $ 集合, $ S $ ∪ $ T = E $ , $ S $ ∩ $ T = \emptyset $
- 割的容量 : $ c(S,T) = \sum _{u ∈ S}^{v ∈T} c(u,v)$
- 割的流量 : $ f(S,T) = \sum_{u \in S} ^ {v \in T} f(u,v) - \sum_{u \in S}^{v \in T} f(v,u)$
- $ \forall $ 可行流 $ f,\forall [S,T],|f| = f(S,T) \le c(S,T)$
割的容量和割的流量是不对称的
最小割指的就是容量最小的割,而由上面的式子可以得到最大流的流量是小于等于最小割的容量的
最大流最小割定理
最大流核心概念捏
内容(以下三个点是等价的,可以互推的):
- 可行流 $ f $ 是最大流
- 可行流 $ f $ 的残留网络中不存在增广路径
- 对于可行流 $ f $ 来说,存在某个割 $ [S,T] $ 使得 $ |f| = c(S,T) $
证明:① <-> ② 显而易见。③ - > ①,由割的公式可以知道, |最大流 $ f $ | $ \leq c(S,T) $ ,所以可以得到 $ |f| = c(S,T) \le $ |最大流|。② -> ③,首先定义以下 $ S $ 为在残留网络中从 $ s $ 出发沿容量大于 $ 0 $ 的边走,所有能到达的边, $ T = V- S $ ,显而易见的是, $ \forall u \in S,v \in T,f(u,v) = c(u,v) $ ,而 $ f(v,u) = 0 $ ,所以这个时候 $ |f| = c(S,T) $ ,因而②可以推③,所以上面三个点是可以互推的捏。
最大流算法
最大流算法一般维护的是残留网络,所以建的是双向边,用领接表存比较好找到反向边
EK
思路:找一个可行流,然后不断找他的残留网络有没有增广路径(用 $ bfs $ 找),如果有的话就更新残留网络,然后再次寻找;没有的话那么这个可行流就是最大流。
时间复杂度: $ O(nm^2) $ (指极限,一般时间复杂度的上界都是非常宽松的(y总锐评:最大流算法的时间复杂度其实就是根本就不用管,就是放屁啊),一般处理1e3 ~ 1e4的网络都可以滴)
存图:领接表,从 $ 0 $ 开始存,然后正反边连续存,成对存储正向边和反向边,这样找反向边就直接 ^ 1就可以了 。 $ Dinic $ 也是这样存图的
模板:
void add(int a,int b,int w) {
e[idx] = b, f[idx] = w,ne[idx] = h[a], h[a] = idx ++;
e[idx] = a, f[idx] = 0,ne[idx] = h[b], h[b] = idx ++;
}
bool bfs() {
memset(flag,0,sizeof flag);
int hh = 0,tt = 0;
q[0] = S;
flag[S] = true,d[S] = inf;
while (hh <= tt) {
auto u = q[hh ++];
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (!flag[v] && f[i]) {
flag[v] = true;
d[v] = min(d[u],f[i]);
pre[v] = i;
if (v == T)
return true;
q[++ tt] = v;
}
}
}
return false;
}
int EK() {
int ans = 0;
while (bfs()) {
ans += d[T];
for (int i = T; i != S; i = e[pre[i] ^ 1]) {
f[pre[i]] -= d[T];
f[pre[i] ^ 1] += d[T];
}
}
return ans;
}
Dinic
思路:和 $ EK $ 一样的就不写了,不一样的就是在每次宽搜的时候不是只找一条增广路径,而是每次在增广残留网络的时候,会先 $bfs $ 一遍,建立分层图,然后在分层图上通过 $ dfs $ 的方式,把所有能够增广的路径全部找出来,然后增广。
时间复杂度: $ O(n^2m) $ ,比 $ EK $ 快,可以处理 $ 1e4 - 1e5 $ 。因为时间复杂度比较玄学,所以优化很重要捏。(y总再次锐评:网络流的时间复杂度不用管啊,网络流的时间复杂度就是一个笑话)
三大优化:
- 当前弧优化
- flow < limit
- 删点
void add(int a,int b,int w){
e[idx] = b,f[idx] = w,ne[idx] = h[a],h[a] = idx ++;
e[idx] = a,f[idx] = 0,ne[idx] = h[b],h[b] = idx ++;
}
int dfs(int u,int limit) {
if (u == T) return limit;
int flow = 0;
for (int i = cur[u]; ~i && flow < limit; i = ne[i]) {
cur[u] = i;//当前弧优化
int v = e[i];
if (de[v] == de[u] + 1 && f[i]) {
int t = dfs(v,min(f[i],limit - flow));
if (!t) de[v] = -1;//删点
f[i] -= t,f[i ^ 1] += t;
flow += t;
}
}
return flow;
}
bool bfs() {
queue<int> q;
q.push(S);
memset(de,-1,sizeof de);
de[S] = 0,cur[S] = h[S];
while (q.size()) {
auto u = q.front();
q.pop();
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (de[v] == -1 && f[i]) {
de[v] = de[u] + 1;
cur[v] = h[v];
if (v == T) return true;
q.push(v);
}
}
}
return false;
}
int dinic() {
int ans = 0,flow;
while (bfs()) {
while (flow = dfs(S,inf),flow) {
ans += flow;
}
}
return ans;
}
ISPA
$ ISPA $ 和 $ dinic $ 的区别是 $ ISPA $ 只用跑一次 $ bfs $ ,然后这一次 $ bfs $ 就建立了一个分层图,并且这里跑 $ bfs $ 的时候是从汇点往源点跑的。然后 $ dfs $ 的操作和 $ dinic $ 是差不多的。虽然这里只用跑一次 $ bfs $ ,但是在每一次 $ dfs $ 的时候是会更新 $ de $ 的值的,当 $ S $ 的深度 $ > n$ 的时候,就结束(所以要从 $ T $ 遍历到 $ S $ 捏。
然后这里的一个 $ gap $ 优化,在下面代码里面看就可以了()。ISAP的核心也在下面的代码里写了捏(
时间复杂度: $ O(mn^2) $
void bfs() {
queue<int> q;
for (int i = 1; i <= n; i ++) {
de[i] = n;
}
q.push(T);//从汇点开始反向BFS,汇点加入队列
de[T] = 0;
while (q.size()) {
auto u = q.front();
q.pop();
for (int i = h[u]; ~ i; i = ne[i]) {
int v = e[i];
if (de[v] == n && f[i ^ 1]) {
//因为bfs用的反向边,容量为0,因此要判断正向边容量是否大于0
de[v] = de[u] + 1;//记录当前点的层次
siz[de[v]] ++;//统计每个层次有几个点
q.push(v);
}
}
}
}
int dfs(int u,int limit) {
if (u == T) {
return limit;
}
int flow = 0;
for (int i = h[u]; ~ i; i = ne[i]) {
int v = e[i];
if (de[u] == de[v] + 1 && f[i]) {//如果这条边的残量大于0,且没有断层
int t = dfs(v,min(f[i],limit - flow));
if (t) {
f[i] -= t;
f[i ^ 1] += t;
flow += t;
}
if (flow == limit) return flow;
}
}
//GAP优化,出现断层,无法到达t了
//为了与下一层分隔开,避免下次还会遍历到下一层
if (-- siz[de[u]] == 0)
de[S] = n + 1;
//Isap核心,到这里,说明入流量有富余,出流量都用完了,提升高度
de[u] ++;//层++
siz[de[u]] ++;//层数对应个数++
return flow;
}
int isap() {
int ans = 0;
bfs();//bfs一次,建立分层图
while (de[S] < n) {
ans += dfs(S,inf);
}
return ans;
}
HLPP
预流推进,主要思想就是:能推流就推流,往大了流,最后看看 $ T $ 有多少水,就是最大流
具体过程:
- 先从 $ S $ 点想周围点推流,然后把周围有余流的点入队( $ S $ 和 $ T $ 在 $ HLPP $ 里面都是不入队的)
- 不断的取队头元素(这里是优先队列,按照深度排序的那种,也就是取出高度最高的点),然后向周围点推流
- 若推完之后还有余流,更新高度标号,重新放入优先队列
- 队列空了的话就返回
但是这就有一个问题,会出现两个点不停地反复推的结果,所以就给每一个点一个高度,让水只能从高处往低出流,而在算法运行的时候,不断地让有余流的点更改高度,直到这些点全部都没有余流。
为什么这样就没有来回推的情况了呢,=>当两个点在来回推流的时候,它们的点会不断上升,当他们的高度大于 $ S $ 的时候,就会把余流退给 $ S $
所以在算法开始之前,要先把 $ S $ 的高度设为 $ n $ ,免得一开始 $ S $ 周围的那些点就把流还给 $ S $ 了。
$ HLPP $ 的优化就是和 $ ISAP $ 一样的 $ gap $ 优化
struct cmp {
//优先队列中按照深度排序
bool operator () (int a,int b) const {
return de[a] < de[b];
}
};
priority_queue<int,vector<int>,cmp> q;
il void pushflow(int u) {
for (int i = h[u]; ~ i; i = ne[i]) {
int v = e[i];
if (f[i] && de[u] == de[v] + 1) {
int t = min(f[i],flow[u]);
flow[u] -= t,flow[v] += t;
f[i] -= t,f[i ^ 1] += t;
if (v != S && v != T && !flag[v]) {
q.push(v);
flag[v] = true;
}
if (!flow[u]) break;
//如果流量已经用完了,提前返回
}
}
}
il void relabel(int u) {
//把u的高度更改为与u相邻的最低的而且还有容量的点的高度 + 1
de[u] = inf;
for (int i = h[u]; ~ i; i = ne[i]) {
int v = e[i];
if (f[i] && de[u] > de[v] + 1)
de[u] = de[v] + 1;
}
}
int que[N];
//建立分层图,从汇点开始
il void bfs() {
int hh = 0,tt = 0;
que[0] = T;
memset(de,-1,sizeof de);
de[T] = 0;
while (hh <= tt) {
int u = que[hh ++];
for (int i = h[u]; ~ i; i = ne[i]) {
int v = e[i];
if (de[v] == -1 && f[i ^ 1]) {
de[v] = de[u] + 1;//记录当前点的层次
que[++ tt] = v;
}
}
}
}
//最大标号预流推进算法
il lwl hlpp() {
bfs();
//如果S和T不连通的话,直接返回-1
if (de[S] == -1)
return 0;
de[S] = n;//设置S的高度为n,避免周围点一开始就把流量还回来了
//统计每一个深度点的数量
for (int i = 1; i <= n; i ++) {
if (de[i] > -1)
siz[de[i]] ++;
}
//从源点预流推进,因为源点不加入队列,就再外面跑了
for (int i = h[S]; ~ i; i = ne[i]) {
int v = e[i],w = f[i];
if (w) {
//一开始把周围的点都堆满流,后续如果多了(有余流),再还回来
flow[S] -= w,flow[v] += w;
f[i] -= w,f[i ^ 1] += w;
if (v != S && v != T && !flag[v])
q.push(v);
}
}
//不断从优先队列取高度最高的点进行推流
while (q.size()) {
auto u = q.top();
q.pop();
flag[u] = false;
pushflow(u);//对u点进行推流
//如果还有余流的话,要往回退流了,提升高度
if (flow[u]) {
siz[de[u]] --;
//断层了,GAP优化
if (! siz[de[u]]) {
for (int i = 1; i <= n; ++ i) {
if (i != T && i != S && de[i] > de[u]) {
de[i] = n + 1;
//标记为无法到达
}
}
}
relabel(u);
//HLPP的特别标记规则,ISAP是直接加加
siz[de[u]] ++;
q.push(u);
flag[u] = true;
}
}
return flow[T];
}
有上下界的网络流
整一个wanqitzh的手绘图()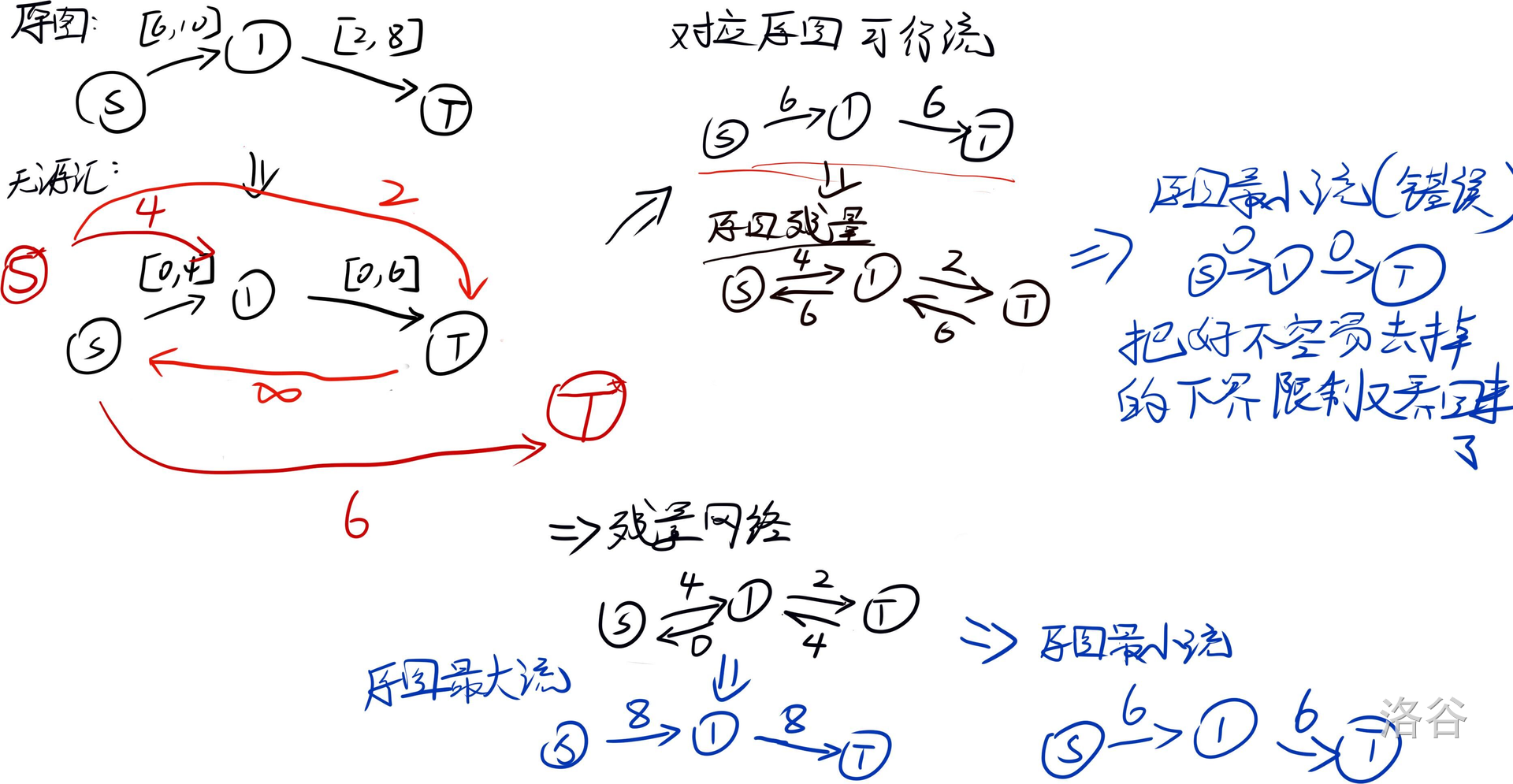
无源汇上下界可行流
建一个虚拟源点和虚拟汇点,然后在连边的时候所有边的容量都减去下界,接下来算一下每一个点的出入,如果入和出不一样,就向源点或者汇点连边,如果源点的出边和(也就是 $ dinic $ 求出来的最大值和之前求的所有多的入的和是一样的,那就说明有解)
然后如果有解的话,每一条边的流量再加上原来的下届就是现在这条边的流量,输出就可以了(),然后就是因为这里 $ f $ 数组存的是残留网络,所以在输出的时候要用 $ f $ [ $ i $ ^ $ 1 $ ] 加上下界。
void add(int a,int b,int up,int down) {
e[idx] = b,f[idx] = up - down;
l[idx] = down,ne[idx] = h[a],h[a] = idx ++;
e[idx] = a,f[idx] = 0,ne[idx] = h[b],h[b] = idx ++;
}
S = 0,T = n + 1;
memset(h,-1,sizeof h);
int a,b,c,d;
for (int i = 1; i <= m; i ++) {
a = fr(),b = fr(),d = fr(),c = fr();
add(a,b,c,d);
w[a] -= d,w[b] += d;
}
for (int i = 1; i <= n; i ++) {
if (w[i] > 0) {
sum += w[i];
add(S,i,w[i],0);
} else if (w[i] < 0) {
add(i,T,-w[i],0);
}
}
int ans = dinic();
if (ans != sum) {
wj;
return 0;
} else {
puts("YES");
for (int i = 0; i < m * 2; i += 2) {
fw(f[i ^ 1] + l[i]);
ch;
}
}
有源汇上下界
这里有最大流和最小流两种,但是因为他们的代码和思路其实都差不多,所以就放一起了。
有源汇的其实建边还有判断有没有解和无源汇是一样的(显而易见),唯一不一样的就是在所有边都建完之后要从 $ t $ 到 $ s $ 连一条 $ inf $ 的边,这是因为后面算流的时候 $ s $ 和 $ t $ 的流量是可以不守恒的( $ s $ 的出可以多, $ t $ 的入可以少)。
接下来因为跑了一遍 $ dinic $ ,所以现在 $ idx - 1 $ 这条边的流量对应的就是现在这个可行流的流量,用一个数记录下来。接下来还要把附加边去掉跑 $ dinic $ ,所以现在需要把附加边去掉。去掉这个比较简单,就是把 $ s $ 和 $ t $ 之间连的那条边去掉就可以了,去掉之后就算从 $ s $ 跑到了 $ S $ ,也不会接着往后面扩展了(因为现在从 $ S $ 往外面连的边都是满流量的,所以从 $ S $ 出去的残留网络 $ f $ 都是 $ 0 $ )
-
再然后,如果是在求最大流的话,就从 $ s $ 往 $ t $ 跑一遍 $ dinic $ ,然后用之前记录的 $ f[idx] $ 加上现在求出来的流量就是最大流。
-
如果求的是最小流的话,就从 $ t $ 往 $ s $ 跑一遍 $ dinic $ ,然后用之前记录的减去现在求的这个就是最大流,其实就是相当于从 $ t $ 往前面找最多可以退回去多少流量
代码,就贴一个最小流的,最大流的都差不多
S = 0,T = n + 1;
for (int i = 1; i <= m; i ++) {
a = fr(), b = fr(),down = fr(),up = fr();
add(a,b,up - down);
w[a] -= down,w[b] += down;
}
for (int i = 1; i <= n; i ++) {
if (w[i] > 0) {
sum += w[i];
add(S,i,w[i]);
} else if (w[i] < 0) {
add(i,T,-w[i]);
}
}
add(t,s,inf);
int ans = dinic();
if (ans < sum) {
wj;
return 0;
} else {
S = s,T = t;
ans = f[idx - 1];
f[idx - 1] = 0,f[idx - 2] = 0;
//删掉所有附加边
int res = dinic();
fw(ans + res);
}
拆点
这是一种网络流常用的(常用吧,应该吧)的方法,就是当一个点他有流过的最大限制的时候,一般是把这个点拆成两个点,然后所有进入这个点的流量连到其中一个点上面,出去这个点的流量连到另外一个点上面去,然后再在这两个点之间连一条容量为这个点流量限制的边。
我看y总的代码一般用的是 $ + n $ ,但是我就喜欢直接乘二和乘二减一,应该都没有关系。
然后拆点的时候要注意的地方就是,开点的数量要开两倍,而且要分清楚哪个是入的点,哪个是出的点,在这两个点之间连边的时候是从入的点连到出的点
连边的代码比较短捏,这是餐饮这道题拆点和连边的一部分代码,主要就是贴贴拆点()
for (int i = 1; i <= n; i ++) {
c = fr(),d = fr();
add(i * 2,i * 2 - 1,1);
for (int j = 1; j <= c; j ++) {
a = fr();
add(N - 5 - a - D,i * 2,1);
}
for (int j = 1; j <= d; j ++) {
b = fr();
add(i * 2 - 1,N - 5 - b,1);
}
}
最小割
前面写过最小割的基本定义了,其实单纯求最小割就是直接跑一遍最大流就可以了,这两个值都是一样的。但是只是最大流流量 = 最小割容量,但是残留网络里面流量为 \(0\) 的边不一定是割边捏
一般最小割会用在每个点二者选其一或者最大权闭合子图这种题目。
求最小割的方案
直接 $ dfs $ 就可以了,弄一个标记数组 $ flag $ 然后从源点开始 $ dfs $ ,每次走残余流量大于 $ 0 $ 的边,也就是说跟 \(S\) 相连的点,然后把那个点标记上(标记了的点就是在 $ S $ 集合的点)
比较简单,也很好懂,代码
void get(int u) {
flag[u] = true;
for (int i = h[u]; ~ i; i = ne[i]) {
int v = e[i];
if (!flag[v] && f[i] > 0) {
get(v);
}
}
}
二者选其一
$ eg $ . 有 $ n $ 个物品和两个集合 $ A $ , $ B $ ,如果一个物品没有放入 $ A $ 集合会花费 $ w_{1i} $ ,如果一个物品没有放入 $ B $ 集合会花费 $ w_{2i} $ ,如果两个物品不在一个集合会花费 $ val_i $ ,求最小花费
这种题就是经典的 二者选其一 的最小割问题。这个题的连边方式是将集合 $ A $ 和 $ B $ 设为源点和汇点,然后根据每一个要求连边。例如上面一种题目,对于 $ w_{1i} $ 这个花费,就向源点连一条权值为 $ w_{1i} $ 的边,然后对于 $ w_{2i} $ 也是差不多的连法。而对于每一个 $ val_i $ ,就在 $ u $ 和 $ v $ 之间连一条容量为 $ val_i $ 的双向边就可以了,然后这样跑出来的最小割( $ dinic $ )就是最小花费了。
二者选其一例题 here
最大权闭合子图
$ eg $ .给定一张有向图,每个点都有一个权值,需要找出一个权值和最大的子图,使每个点的后继都在子图中,求权值和最大为多少
做法 :建立超级源点 $ S $ 和超级汇点 $ T $ ,如果节点 $ u $ 的权值为正,就从 $ S $ 连一条边,如果权值为负,就向 $ T $ 连一条边。然后把所有正点权都加到 $ sum $ 里面去,然后对于原图中的每一条边都连上,然后把容量设置为 $ inf $ 。然后跑一个最小割,最后用 $ sum $ 减去跑出来的答案就是要求的最大权值和
最大权闭合子图例题 here
证明
-
每一个符合条件的子图都对应着流量网络中的一个割。因为每一个割将网络分为两个部分,与 $ S $ 相连的点满足没有边指向另一部分,男足条件
-
最小割所去除的边必须与 $ S $ 或者 $ T $ 相连,也就是说不会去掉原图中的边。因为原图中的边连的边权是 $ inf $ ,如果去掉了就不是最小割了。
-
选择的那部分子图的权值和是所有正权值之和 - 没有选择的正权点权值之和 - 选择的负权值(此处是绝对值)之和(显而易见)。而当我们不选择一个正权点的时候,在最小割中的体现就是断掉它和 $ S $ 之间的边;当我们选择一个负权边的时候,它和 $ T $ 的连边就会被断掉。也就是说我们求出的最小割就是(没有选择的正权点权值和 + 选择的负权点权值之和),所以就可以把上面的权值和转化成
最大权值和 = 所有正权值之和 - 最小割
其它的一些
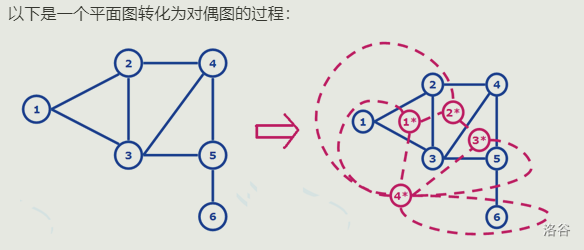
平面图和对偶图
平面图定义:如果 $ G $ 的任何两条边都没有除了顶点外的交点,那就是平面图(在 $ oiwiki $ 上是:{如果图 $ G $ 能画在平面 $ S $ 上,即除了顶点外无边相交,则称 $ G $ 可平面嵌入 $ S $ , $ G $ 为可平面图或平面图。画出的没有边相交的图称为 $ G $ 的平面表示或者平面嵌入。},但是以我现在的理解能力还看不懂,所以先放着)
然后下面的 $ G $ 都是一个平面图
面:由 $ G $ 的边将 $ G $ 所在的平面划分成若干个区域,每个区域称为 $ G $ 的一个面。期中面积无限的面(不是被围起来的封闭图形)称为无限面或者外部面,面积有限的(封闭图形)称为有限面或者内部面。包围每个面的所有边组成的回路称为该面的边界,边界的长度称为该面的次数。
平面中所有面的次数之和等于原图边数的两倍(每个边都在两个面中,会算两次)
极大平面图 :若在 $ G $ 的任意不相邻顶点间添加边,所得的图为非平面图,那么 $ G $ 是极大平面图。若 $ G $ 为 $ n(n \ge 3) $ 阶的连通平面图,那么 $ G $ 为极大平面图当且仅当 $ G $ 的每个面的次数均为 $ 3 $ 。
对偶图 : $ G $ 为平面图的某一个平面嵌入,构造 $ G^* $ 。
-
在 $ G $ 的每一个面 $ R_i $ 中放置 $ G^* $ 的一个顶点 $ {u_i}^* $
-
设 \(e\) 为 \(G\) 的一条边,若 \(e\) 在 \(G\) 的面 \(R_i\) 和 \(R_j\) 的公共边界上,做 \(G^{* }\) 的边 \(e^{* }\) 与 \(e\) 相交,且 $e^* $ 关联 \(G^{* }\) 的顶点 $v_i^* $, $v_j^* $,即 \(e^* =(v_i^* , v_j^* )\),$e^* $ 不与其他任何边相交。若 \(e\) 为 \(G\) 中桥且在 \(R_i\) 的边界上,则 $e^* $ 是以 \(R_i\) 中顶点 $v_i^* $ 为端点的环,即 $ e^* = (v^{* }_i,v^{* }_j)$
平面图转成对偶图之后,有一个性质:平面图最小割 = 对偶图最短路。例题 here
最大密度子图
给定无向图 \(G=(V,E)\) ,其子图记为 \(G^* =(V^* ,E^* )\) ,在所有子图构成的集合中,密度 \(D=|E^* ||V^* |\) 最大的元素称为最大密度子图。
原理
首先先进行二分,二分出一个 $ g $ (密度),对于 $ max(|E ^ * | - g * |V ^ * |) $ ,如果它大于 $ 0 $ ,那么说明答案更大,否则答案更小。
但是怎么求 $ max(|E ^ * | - g * |V ^ * |) $ 呢?先将它写成一个以 $ g $ 为自变量的函数 $ h(g) $ 。但是现在这个式子没有什么好求的性质,于是尝试向最小割转化。
首先令 $ cnt[V',\overline{V^* }] $ 表示 不在子图 $ G ^ * $ 内部边的个数, $ d[u] $ 表示点 $ u $ 的度数
对于 $ |E^* | $ ,有:
$ |E'| = \frac{\sum_{u\in V'}d_u - cnt[V',\overline{V'}]}{2} $
也就是说对于 $ h(g) $ 来说,我们有
$ h(g) = \frac{1}{2}(\sum_{u\in V'}d_u - cnt[V',\overline{V'}]-2g|V'|) $
而对于 $ 2g|V'| = \sum_{u\in V'}2g $ ,我们有
$ h(g) = \frac{1}{2}(\sum_{u\in V'}{(d_u-2g)} - cnt[V',\overline{V'}]) $
因为要转化为最小割,所以要转化成最小化 $ - h(g) $
$ -h(g) = \frac{1}{2}(\sum_{u\in V'}{(2g-d_u)} + cnt[V',\overline{V'}]) $
于是乎就这个样子建图:
- 原图中的边两个点之间连接容量为 $ 1 $ 的双向边。
- $ V $ 中的点 $ u $ 向汇点 $ T $ 连接容量为 $ 2g - d_u + U $ 的边。( $ U $ 为一个保证容量非负的数)
- 源点 $ S $ 向点 $ u $ 连接一条容量为 $ U $ 的边
证明
对于一个割而言,容量满足:
$ c[s,t]=\sum_{u\in \overline{V'}}U + \sum_{u\in V'}(2g-d_u+U) + \sum_{u\in V'}\sum_{v\in \overline{V'}}c(u,v) $
转化一下(把两个$ U $都提出来, $ |V|'+|\overline{V'}| = |V| $ ):
$ c[s,t]=|V|U + \sum_{u\in V'}(2g-d_u) + \sum_{u\in V'}\sum_{v\in \overline{V'}}c(u,v) $
而可以发现 :
$ \sum_{u\in V'}(-d_u) + \sum_{u\in V'}\sum_{v\in \overline{V'}}c(u,v) $ 恰好就是 $ -2|E'| $
故而可以推得:
$ c[s,t]=|V|U + \sum_{u\in V'}(2g) - 2|E'| $
整理一下得:
$ c[s,t]=|V|U + 2(g|V'| - |E'|) $
这就意味着最小割对应着最小的 $ -h(g) = g|V'| - |E'| $ ,也就是最大的 $ h(g) = |E'| - g|V'| $ ,这样就解决了()
在具体实现的时候, $ U $ 是为了保证容量非负,所以$ U = |E'| $ 就可以。
费用流
含义:所有最大可行流当中,费用的最大值和最小值。定义每一条的费用为 $ w(u,v) $ 。相当于每一个管道有一个运输成本(?)
可行流的费用: $ \sum_{u \in V}^{v \in V} f(u,v)* w(u,v)$
如果 $ G $ 有最大流,它不一定可以把最小费用最大流求出来(是有的),就像下面这个图(黑色的是容量,蓝色的是费用):
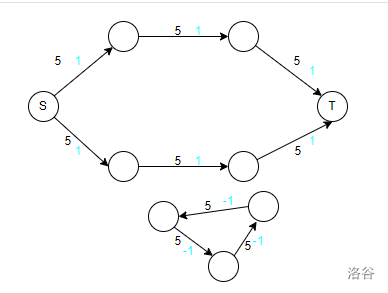
求法:把之前的 $ EK $ 算法里面的 $ bfs $ 换成 $ spfa $ 就可以了。 $ spfa $ 里面的最短路径的标准按照费用来跑,也就是说这里的边权按照费用和流量的乘积跑,但是这里的 $ spfa $ 是没有办法处理有负环的图的。
然后显而易见的是,求最小费用就用最短路的板子,求最大费用就用最长路的板子
模板
具体的看上面的 $ EK $ 算法,这里就提个代码了捏。具体思路就是上面的 $ EK $ ,不知道这里能不能用 $ dij $ ,但是懒得写了。
然后这里 $ spfa $ 的清空要注意一下,本来所有 $ minf $ 都是要清空的,但是 $ spfa $ 跑完之后要的只有 $ minf[T] $ ,所以就不用全部清空,直接 $ min[T] = 0 $ 就可以咯。然后好像 $ flag $ 可以清空也可以不清空,我写 $ spfa $ 习惯了把 $ flag $ 清空,所以就懒得改了,到时候如果被卡掉了再改吧
void add(int a,int b,int wf,int ww) {
e[idx] = b,f[idx] = wf,w[idx] = ww;
ne[idx] = h[a],h[a] = idx ++;
e[idx] = a,f[idx] = 0,w[idx] = -ww;
ne[idx] = h[b],h[b] = idx ++;
}
bool spfa() {
queue<int> q;
memset(flag,0,sizeof flag);
memset(dis,0x3f,sizeof dis);
minf[T] = 0;
q.push(S);
flag[S] = true,minf[S] = inf;
dis[S] = 0;
while (q.size()) {
auto u = q.front();
q.pop();
flag[u] = false;
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (f[i] && dis[v] > dis[u] + w[i]) {
dis[v] = dis[u] + w[i];
pre[v] = i;
minf[v] = min(minf[u],f[i]);
if (!flag[v]) {
flag[v] = true;
q.push(v);
}
}
}
}
return minf[T] > 0;
}
void EK() {
flow = 0,cost = 0;
while (spfa()) {
flow += minf[T];
cost += minf[T] * dis[T];
for (int i = T;i != S; i = e[pre[i] ^ 1]){
f[pre[i]] -= minf[T];
f[pre[i] ^ 1] += minf[T];
}
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号