层次聚类

目录

1.层次聚类的原理

2.层次聚类优缺点

3.聚类实例

---

 

1.层次聚类的原理

层次聚类可以分为两种主要类型：凝聚型（agglomerative）和分裂型（divisive）。

　　1.凝聚聚类：它也被称为AGNES（凝聚嵌套）。 它以自下而上的方式工作。 也就是说，每个对象最初被认为是单元素簇（叶子）。 在算法的每个步骤中，将最相似的两个群集组合成新的更大的群集（节点）。 迭代此过程，直到所有点都只是一个单个大簇（root）的成员（参见下图）。 结果是一棵树，可以绘制为树状图。

　　2.分裂层次聚类：它也被称为DIANA（Divise Analysis），它以自上而下的方式工作。 该算法是AGNES的逆序。 它以root开头，其中所有对象都包含在单个集群中。 在迭代的每个步骤中，最异构的集群被分成两个。 迭代该过程，直到所有对象都在它们自己的集群中（见下图）。

  　其中，凝聚聚类擅长识别小聚类。 分裂层次聚类擅长识别大型集群。

 

然而，我们如何衡量两组观测之间的差异？ 已经开发了许多不同的聚类聚集方法（即连接方法）来回答这个问题。 最常见的类型方法是：

•  最大或完全链接聚类(Maximum or complete linkage clustering)：它计算聚类1中元素和聚类2中元素之间的所有成对不相似性，并将这些不相似性的最大值（即最大值）视为两个聚类之间的距离。 它倾向于产生更紧凑的簇。
• 最小或单链接聚类(Minimum or single linkage clustering)：它计算聚类1中的元素和聚类2中的元素之间的所有成对不相似性，并将这些不相似性中的最小值视为链接标准。 它倾向于产生长而“松散”的簇。
• 平均或平均链接聚类(Mean or average linkage clustering)：它计算聚类1中的元素与聚类2中的元素之间的所有成对不相似性，并将这些不相似性的平均值视为两个聚类之间的距离。
• 质心连锁聚类(Centroid linkage clustering)：它计算聚类1的质心（长度为p变量的平均向量）与聚类2的质心之间的不相似性。
• Ward的最小方差方法(Ward’s minimum variance method)：它最小化了整个群内方差。 在每个步骤中，合并具有最小簇间距离的一对簇。

 

2.层次聚类优缺点

优点：

• 距离和规则的相似度容易定义，限制少
• 不需要预先制定聚类数
• 可以发现类的层次关系
• 对大样本数据效果较好

缺点：

• 计算复杂度太高
• 奇异值也能产生很大影响
• 算法很可能聚类成链状

3.聚类实例

 

 

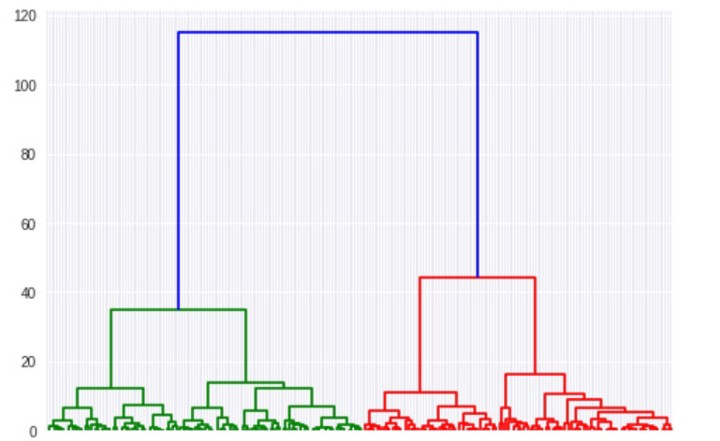
　　树形图绘制出每个簇和距离。 我们可以使用树形图找到我们选择的任何数字的聚类。 在上面的树形图中，很容易看到第一个簇（蓝色），第二个簇（红色）和第三个簇（绿色）的起点。 这里只对前3个进行了颜色编码，但是如果你查看树形图的红色边，你也可以发现第4个簇的起始点。 树形图一直运行，直到每个点都是它自己的单个簇。

让我们看看凝聚层次聚类如何在Python中运行。 首先，让我们从scipy.cluster.hierarchy和sklearn.clustering导入必要的库。

 

# import statements
from sklearn.datasets import make_blobs
import numpy as np
import matplotlib.pyplot as plt


# create blobs
data = make_blobs(n_samples=200, n_features=2, centers=4, cluster_std=1.6, random_state=50)

# create np array for data points
points = data[0]

# create scatter plot
plt.scatter(data[0][:,0], data[0][:,1], c=data[1], cmap='viridis')
plt.xlim(-15,15)
plt.ylim(-15,15)
plt.show()

 

　　现在，让我们创建我们的树形图（我已经在上面展示过），确定我们想要多少个簇，并保存这些簇中的数据点以将它们绘制出来。

#define distance using euclidean
disMat = sch.distance.pdist(points,'euclidean') 

#define the linkage_matrix using ward clustering pre-computed distances 
linkage_matrix=sch.linkage(disMat, method ='ward') #optonal :average ward etc

fig, ax = plt.subplots(figsize=(15, 20)) # set size
ax = sch.dendrogram(linkage_matrix, orientation="right")  #, labels=titles);#可添加label

plt.tick_params(\
    axis= 'x',          # changes apply to the x-axis
    which='both',      # both major and minor ticks are affected
    bottom='off',      # ticks along the bottom edge are off
    top='off',         # ticks along the top edge are off
    labelbottom='off')

plt.tight_layout() #show plot with tight layout

这段代码显示的图像要比上边的图像更美观，更清晰，由于样本数较多，就不在此展示了。

还可以利用散点图展示聚类的结果：

from sklearn.cluster import AgglomerativeClustering

# create clusters
hc = AgglomerativeClustering(n_clusters=4, affinity = 'euclidean', linkage = 'ward')
# save clusters for chart
y_hc = hc.fit_predict(points)


plt.scatter(points[y_hc ==0,0], points[y_hc == 0,1], s=100, c='red')
plt.scatter(points[y_hc==1,0], points[y_hc == 1,1], s=100, c='black')
plt.scatter(points[y_hc ==2,0], points[y_hc == 2,1], s=100, c='blue')
plt.scatter(points[y_hc ==3,0], points[y_hc == 3,1], s=100, c='cyan')

也可以展示热力图：

import seaborn as sns 

sns.clustermap(points,method ='ward',metric='euclidean')

 

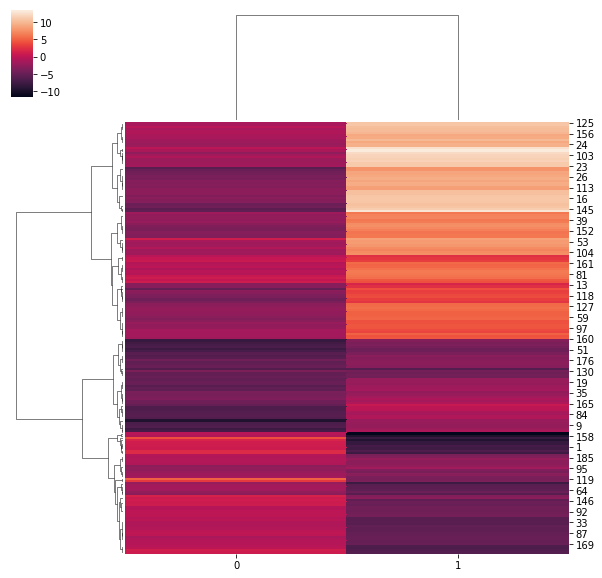
参考：

https://blog.csdn.net/qq_19528953/article/details/79133889（距离公式详解）

https://blog.csdn.net/enigma_tong/article/details/79081449（聚类函数参数详解）