python数学工具(一)
python 数学工具包括:
1.函数的逼近
1.1.回归
1.2.插值
2.凸优化
3.积分
4.符号数学
本文介绍函数的逼近的回归方法
1.作为基函数的单项式
对函数 ![]() 的拟合
的拟合
首先定义函数并且可视化
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
def f(x):
return np.sin(x)+0.5*x
x=np.linspace(-2*np.pi,2*np.pi,50)
plt.plot(x,f(x),'b')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid(True)
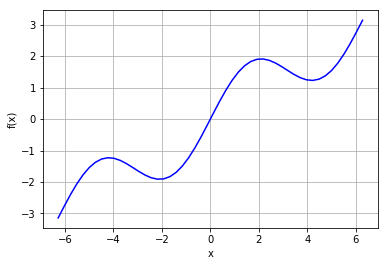
先用一次函数拟合
reg=np.polyfit(x,f(x),deg=1) ry=np.polyval(reg,x) plt.plot(x,f(x),'b',label='f(x)') plt.grid(True) plt.plot(x,ry,'r.',label='reg') plt.legend(loc=0)
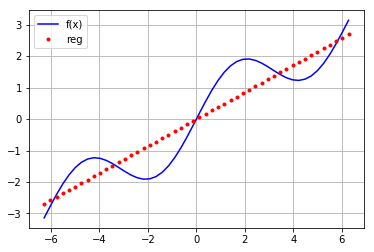
再用高次函数进行拟合
reg=np.polyfit(x,f(x),deg=16) ry=np.polyval(reg,x) plt.plot(x,f(x),'b',label='f(x)') plt.grid(True) plt.plot(x,ry,'r.',label='reg') plt.legend(loc=0)
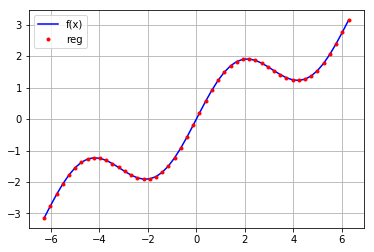
拟合效果的检查
print('平均误差:',sum((ry-f(x))**2)/len(x))
平均误差: 3.16518401761e-13
np.allclose(ry,f(x)) True
2.单独的基函数
首先常见一个空的矩阵,然后为任一行添加函数
mat=np.zeros((3+1,len(x))) mat[3,:]=x**3 mat[2,:]=x**2 mat[1,:]=x mat[0,:]=1
reg=np.linalg.lstsq(mat.T,f(x))
#输出系数
reg[0]
array([ 1.52685368e-14, 5.62777448e-01, -1.11022302e-15,
-5.43553615e-03])
#输出图形 ry=np.dot(reg[0],mat) plt.plot(x,f(x),'b',label='f(x)') plt.plot(x,ry,'r.',label='reg') plt.grid(True) plt.legend(loc=0)
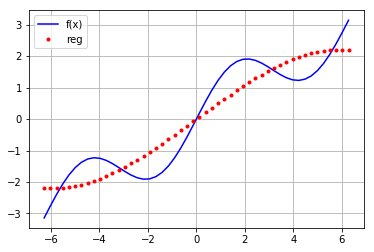
对每行的基函数进行变换:
mat=np.zeros((3+1,len(x))) mat[3,:]=np.sin(x) mat[2,:]=x**2 mat[1,:]=x mat[0,:]=1 reg=np.linalg.lstsq(mat.T,f(x)) ry=np.dot(reg[0],mat) plt.plot(x,f(x),'b',label='f(x)') plt.plot(x,ry,'r.',label='reg') plt.grid(True) plt.legend(loc=0)
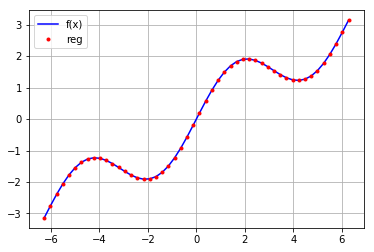
3.多维情形
def fm(x,y):
return np.sin(x) + 0.25 * x + np.sqrt(y) + 0.05**y*2
x = np.linspace(0, 10, 20)
y = np.linspace(0, 10, 20)
x, y = np. meshgrid( x, y)
Z = fm(x,y)
x = x.flatten()
y = x. flatten()
import statsmodels.api as sm
matrix=np.zeros((len(x),6+1))
matrix[:,6] = np.sqrt(y)
matrix[:,5] = np.sin(x)
matrix[:,4] = y**2
matrix[:,3] = y**2
matrix[:,2] = y
matrix[:,1] = x
matrix[:,0] = 1
res=sm.OLS(fm(x,y),matrix).fit()
print(res.summary().as_text())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.999
Model: OLS Adj. R-squared: 0.999
Method: Least Squares F-statistic: 9.605e+04
Date: Tue, 31 Jul 2018 Prob (F-statistic): 0.00
Time: 10:51:36 Log-Likelihood: 661.47
No. Observations: 400 AIC: -1313.
Df Residuals: 395 BIC: -1293.
Df Model: 4
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 1.9548 0.010 193.732 0.000 1.935 1.975
x1 0.5891 0.005 111.546 0.000 0.579 0.600
x2 0.5891 0.005 111.546 0.000 0.579 0.600
x3 -0.0150 0.000 -54.014 0.000 -0.016 -0.014
x4 -0.0150 0.000 -54.014 0.000 -0.016 -0.014
x5 0.9533 0.004 251.168 0.000 0.946 0.961
x6 -1.6190 0.020 -79.979 0.000 -1.659 -1.579
==============================================================================
Omnibus: 4.352 Durbin-Watson: 0.880
Prob(Omnibus): 0.113 Jarque-Bera (JB): 4.214
Skew: -0.208 Prob(JB): 0.122
Kurtosis: 2.717 Cond. No. 4.93e+17
==============================================================================


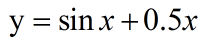 的拟合
的拟合
 浙公网安备 33010602011771号
浙公网安备 33010602011771号