图联通

P3436 [POI2006] PRO-Professor Szu

求 scc 后变为 DAG，随便 dp 就好了。

吐槽数据不对题面，细节巨多。但是肯定不够紫题。

P3469 [POI2008] BLO-Blockade

500年前就做过了，又写了一遍，用了圆方树逃课。就是树上经过每个点的路径数量。

P2860 [USACO06JAN] Redundant Paths G

好题。边双缩点后成一棵树，易得答案下界为 \(\lfloor\dfrac{\text{叶子数+1}}{2}\rfloor\)，毕竟每个叶子都要至少连一条边出去。

接下来证明这个下界可以取到：

最优方案必然是只在叶子节点间连边。考虑每连完一条边就进行一次缩点，保证每连完一次都是一棵树。

当叶子数是偶数时，若连完一条边，叶子数减少 \(2\)，那么这条边合法，因为此时我们用了一条边使答案下界减一，相当于答案不变，是优的。

若连完一条边，叶子数减少 \(1\)，那么是不优的，因为用了一条边，答案下界不变，相当于浪费了一条边。这种情况是需要避免的。

考虑这种情况是什么。

只能是连完边以后的环缩完以后又变成了一个叶子。即环连出的边只有一条。找出这条边在环上的点，那么连成环前这个点 \(u\) 连的边一定长这样：

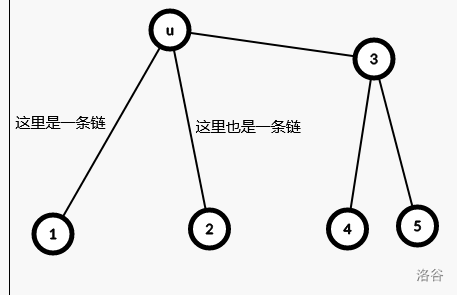
其中 \(1,2,4,5\) 都是叶子。由于在讨论偶数个节点，不考虑 \(3\) 为叶子的情况。 \(3\) 到 \(4,5\)的边上可能有多个点或支链。

此时连接 \((1,2)\) 是不优的。但是因为必然存在上图的结构，即叶子数 \(>2\) （叶子数等于 2 的时候非常平凡）点 \(4,5\) 必然存在。此时连接 \((1,4)(1,5)(2,4)(2,5)\) 任意一个均是合法的。

至此证明了偶数个叶子的情况可取得下界。

奇数叶子情况同样不难，任意连一条即可转化为 \((\text{叶子数-2})\) 或 \((\text{叶子数-1})\) 的情况，易得都能花一条边使下界减一，所以不论怎么连都是优的。

至此证毕。

CF51F Caterpillar

边双缩点后每个联通块找直径作为作最后的链。

至于直径为什么是对的。。。

一个连通块中节点数是一定的，除了最终选择的链上的点，所有叶子都将成为毛毛虫的一部分。同时最终的链一定消耗两个叶子（不然不优）。于是链越长，需要合并掉的点数就越少。所以直径是对的。

P4819 [中山市选] 杀人游戏

答案应该是 \(1-\dfrac{\text{冒险询问次数}}{n}\)。

首先观察到，一个 scc 内只需一次冒险询问即可获得所有点的信息；缩完点后的 DAG 上 询问入度为 0 的点优于不为 0 的点，因为能获得更多信息。

那么冒险询问次数因该就是缩完点后入度等于 0 的 scc 数。但是有特殊情况。

若一个点所在的 scc 大小为 1 且入度为 0，同时不询问这个点能获得其他点的所有信息，那么这个点就没有必要问了。可以少问一次。

“不询问这个点能获得其他点的所有信息” 等价于其所有出边连向的点的入度（不算重边） \(\ge 2\)。

显然存在多个这样的点时只能有一个做出贡献。

P4630 [APIO2018] 铁人两项

圆方树。

枚举 \(s,f\)，考虑哪些点可能成为 \(c\)。

由于圆方树不改变点之间的必经性，所以应该是圆方树上两个点路径上经过的所有点（方点代表周围的点双里的圆点），相同的点算一次。

将方点权值设为代表的点双大小，圆点权值为 \(-1\)，可以完美规避算重割点的情况。

接下来就是树上所有路径的权值和了。

P4606 [SDOI2018] 战略游戏

就是建完圆方树后询问点组成的虚树中经过的圆点数减询问点数。

当然可以无脑拍一棵虚树上去，但是我们有更优美的方式。

性质：任意一棵树讲解点按 dfn 排序后相邻点（第一个和最后一个相邻）为端点的链能刚好把树上每条边覆盖两次。

我们把圆点连向父亲的边权赋为 1，方点连向父亲的边权赋为 0，然后将询问点按 dfn 排序，并进行相邻点组成的链的覆盖，那么虚树上的每条边都被经过两次，即圆点数等于 \(\sum\text{链权}\times \dfrac{1}{2}\)。

特判虚树根为圆点的情况，因为此时根不会被算进去。多加个1就行了。

CF487E Tourists

先建圆方树。

修改圆点时，我们理应修改所有相邻的方点权值，菊花随便卡。

转换思路，对于方点我们只记录它周围除了父亲之外的圆点的 multiset（便于修改）。这时若询问链的 lca 为圆点，那么所有链上方点的父亲都会出现在链上，答案没有影响； lca 为方点时除了 lca 的父亲圆点外所有权值均出现在链上，特殊处理，取个 \(\min\) 就行了。

链 \(\min\) 树剖。

AT_arc092_d [ARC092F] Two Faced Edges

若边 \((u,v)\) 反向对强连通分量有影响，那么应该满足：

• 原图存在 \(v \to u\) 的路径。

• 原图存在不经过边 \((u,v)\) 的 \(u\to v\) 的路径。

这两个仅有一个成立。

1. 均不满足：正着反着都不在一个强连通分量里。

2. 均满足：这俩路径拼起来就是一个 scc，和 \((u,v)\) 方向无关。

3. 满足一个：

• 只满足第一个： \(u\) 和 \(v\) 原来在一个 scc 里，反向以后不在。

• 只满足第一个： \(u\) 和 \(v\) 原来不在一个 scc 里，反向以后在。

---

第一个条件好判， \(O(nm)\) 跑一遍每个点出发的 dfs就行了。

第二个条件不好判，我们考虑队长的方法。

本质是求 \((u.v)\) 是不是 \(u\to v\) 的必经边。

给 \(u\) 的出边编号，求出 \(u\) 到每个点的最小编号出边和最大编号出边（正着跑和倒着跑）。相当于用出边编号对图进行染色。若 \(u\) 到 \(v\) 的最小编号等于最大编号那就是必经边。